“平均数”单元整体教学设计

平均数是统计学中最基础、最重要的概念之一，隶属于“数据的收集、整理与表达”主题。平均数在现行的小学数学教材中并不是独立的单元，一般与条形统计图等内容混合编排。依照《义务教育数学课程标准（2022年版）》编写的人教版新教材中，“平均数”是作为一个单元单独编排的。本文中的“平均数”单元指的是由“认识平均数”及“体会平均数的简单应用”等课时组成的小单元。

一、确定指向核心素养的单元学习目标

1. 基于主题提炼核心概念及单元具体观念

“数据的收集、整理与表达”主题的核心概念是数据意识，数据意识在本单元中的具体表现是“知道在现实生活中，有许多问题应当先做调查研究，收集数据，感悟数据蕴含的信息；知道同样的事情每次收集到的数据可能不同，而只要有足够的数据就可能从中发现规律”。

平均数是表示一组数据“集中趋势”的统计量，代表了这组数据的整体水平。因此，平均数教学要引导学生在熟悉的情境中理解平均数所具有的“代表性”，这是数据意识的本质体现。

基于课程标准及平均数的本质，可以将核心概念具体化为如下单元观念。

观念1：数据蕴含着信息。用平均数可以代表一组数据的整体水平，平均数并不是客观存在的，是通过加工原始数据“匀一匀”得到的。

观念2：平均数具有“敏感性”（平均数对一组数据中的每个数值的变化都较为敏感，尤其容易受到极端数据的影响）和“有界性”（平均数的取值范围在一组数据的最大值与最小值之间）的特点，根据平均数的特性可以解释或解决生活中有关平均数的简单问题。

观念3：知道对于同样的事情每次收集到的数据可能不同，平均数具有随机性，运用随机数据求得的平均数所得到的结论更加公平合理。

2. 多版本教材对比分析

现行小学数学教材一般将“平均数”编排在四年级，多种版本教材都结合具体情境让学生体会平均数是一组数据平均水平的代表，介绍了“移多补少”和“求和均分”等计算平均数的方法。苏教版教材还在“你知道吗”中介绍了“在演唱比赛中……计算选手的得分时，往往要去掉一个最高分和一个最低分……可以剔除一些极端数据……更能代表选手的实际水平”的知识，拓展学生对平均数的认识。

3. 参考权威考试命题

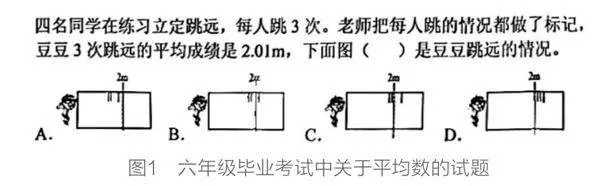
下面是六年级毕业考试中的一道题目（见图1）：

此题考查的是对平均数的本质及特性—“有界性”—的理解，即平均数介于一组数据的最大值与最小值之间。又如下题（见图2）：

此题考查学生对平均数的“敏感性”的理解，平均数很“敏感”，易受极端数据的影响。因此，在实际应用时要先去掉极端数据之后再求平均数，此时的平均数会更具“代表性”，做出的推断也更合理。

可见，素养立意下的考试命题更加注重学生对数学知识本质的理解及思维过程，关注学生对数学概念、性质等的理解与应用。

4. 确定单元学习目标

综合以上分析，依据课程标准和单元具体观念，确定单元学习目标如下：

①在熟悉的情境中体验、理解平均数所具有的“代表性”，感悟数据蕴含的信息，能够解释用平均数代表一组数据整体水平的合理性，能运用“移多补少”“先求和再均分”等方法计算平均数。

②知道平均数不是实际存在的数值，是通过“匀一匀”加工出来的；知道平均数是个“不大不小”的数，取值范围在一组数据的最大值和最小值之间；知道平均数对一组数据中的每个数值的变化都较为敏感，尤其容易受到极端数据的影响。

③初步感受平均数的推断功能，能运用平均数的特性对真实情境中“去掉最低分和最高分再取平均数”的数据处理方法进行解释，知道在实际应用时要先去掉极端数据之后再求平均数，此时的平均数会更具“代表性”，做出的推断也更合理。

二、单元内容重组与课时规划

1. 厘清单元内容的学习进阶

基于上述分析，确定“平均数”单元内容的学习进阶如下。层级1：会用“先求和再均分”或“移多补少”的方法计算一组数据的平均数。层级2：知道平均数能够代表一组数据的整体水平（平均水平），体验平均数的“敏感性”“有界性”等特性。层级3：能够解释并体会平均数作为“代表”的合理性，感受平均数的推断功能，知道去掉极端数据后所得到的平均数更有代表性，推断更合理，知道平均数具有随机性。

其中，层级1属于对平均数理解的“算法水平”，学生有相应的知识基础，较容易达成；层级2属于“概念水平”，层级3属于“统计水平”，较难达成。因此，可以将本单元分为两个课时，第一课时着眼于“层级1和层级2”的达成，第二课时则聚焦于“层级3”的达成。

2. 学情调研

学生早在二年级时就会用除法解决“平均分”的问题。虽然“平均分”和平均数的意义不同，但计算方法一样，因此学生掌握平均数的算法相对容易。调研发现，95%以上的学生会用已有知识“总数÷份数=平均数”计算平均数；但只有不到10%的学生能比较含糊地说出平均数的含义；对于平均数是小数的情况，有近95%的学生表示不能理解，认为是错误的；另外，学生缺乏用一个数代表一组数的经验，很难想到用平均数作为一组数据的代表数。

3. 设计指向目标的核心任务序列

基于上述分析，笔者重构了平均数的单元内容。

（1）关键课

教学内容：认识平均数。

核心目标：①结合游戏情境和几何直观，认识平均数的“代表性”，能用“先求和再均分”“移多补少”等方法求出平均数；②结合真实情境和几何直观，体会平均数的“虚拟性”“有界性”和“敏感性”；③初步感受平均数的推断功能。

核心任务设计：任务1—玩“记数游戏”，比一比“谁的记数水平高”；任务2—用“求和均分”和“移多补少”的方法求平均数；任务3—观察直观图，说出你的发现（讨论：如果再玩一次，5次的平均数和4次的平均数一样吗？为什么？）；任务4—乐乐前四次的计数成绩分别是6、8、7、3，她第五次能记住几个数？请说明理由。

（2）练习拓展课

教学内容：平均数的再认识。

核心目标：①能运用平均数的“有界性”解决真实情境中的问题；②能够结合真实情境，对“先去掉极端数据再求平均数”的方法进行解释，知道这时的平均数会更具“代表性”，做出的推断也更合理。

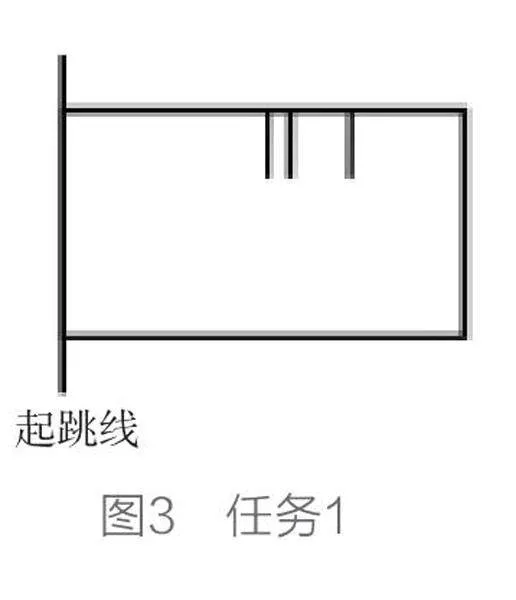
核心任务设计：任务1—体育老师用示意图表示了乐乐跳远的情况（见图3）。图中三条短实线所在的位置代表她三次跳远的成绩。如果用虚线所在的位置表示她三次跳远的平均成绩，请你画出这条虚线，并解释这样画的理由。

任务2—陈飞制作了一个简易摆钟，他想测出这个摆钟摆动60次所用的时间，于是做了一次实验，并邀请8位同学分别计时，得到了下面的数据（单位：秒）（见图4）。结合数据，想要更准确地得到摆钟摆动60次所用的时间，你建议使用什么方法？请说明理由。

三、关键课教学举例—“认识平均数”

1. 环节一：情境引入，寻找代表数

师生一起玩记数游戏。教师出示游戏规则：每次屏幕上会出现10个数字，只能观察2秒，把记住的数字写下来（可以不按顺序），看自己每次可以记住几个数字，每人玩三次。

【思考】游戏情境紧紧抓住了学生的心，学生精力高度集中，迅速进入学习状态，为接下来的数据分析奠定良好基础。

2. 环节二：借助直观，认识平均数的代表性

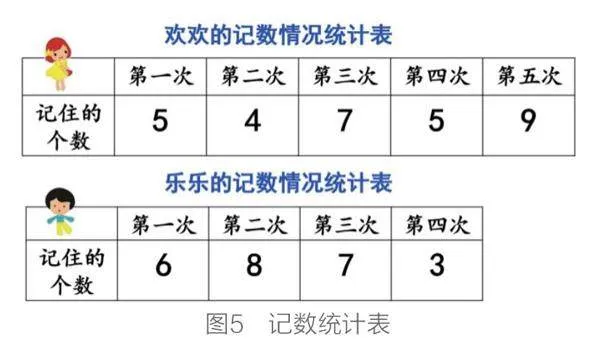
教师出示记数统计表（见图5）：

师：比一比，谁的记数水平高？

生1：我觉得欢欢的水平高，因为她有一次记住了9个，乐乐的都比9个少。

生2：我不同意，欢欢只有一次记住了9个，其他几次都比9个少，这样不公平！

生3：可以把这几个数加起来，5+4+7+5+9=30，6+8+7+3=24，30>24，所以欢欢的记数水平高。

生4：我不同意！欢欢玩了5次，乐乐只玩了4次，5次的成绩当然比4次的成绩好啦，这对乐乐不公平！

生5：她俩玩的次数不同，比较总数不公平。我觉得可以用5+4+7+5+9=30，再用30÷5=6（个）；用6+8+7+3=24，24÷4=6（个），她俩的记数水平dc4a941a170c12d55f48c6186dfb0131bd45cc645e422f99a63103b3b2cb4e09一样。

……

学生意见不一，争执不下。

师：我们可以把这些数据整理一下，看看直观的统计图能不能帮助我们选择合适的代表数（见图6）。

课件逐次动态呈现，教师引导学生借助直观图讨论：用哪个数代表这组数据的整体水平更合理、更公平？

生1：4是最小数，不能代表整体水平；9是最大数，也不能代表整体水平；5虽然在“中间”，但是比5小的只有4，而且只少了1个；但是，比5大的有7和9，而且多了好几个，所以5不能代表整体水平。7也不行，因为比7大的只有9，只多了2个，但是比7小的有很多。

教师动态呈现“移多补少”的过程（见图7）。

师：可以把“多的”移走，补给“少的”，这种方法叫“移多补少”，得到的6是这组数据的平均数。你觉得平均数6能代表这组数据的整体水平吗？

生1：能！因为现在每次的数都是6了。

师：是的，平均数6代表了这5个数的整体水平，而不是某一次的水平。你觉得用平均数代表欢欢和乐乐的记数水平，公平吗？

生1：公平！

【思考】学习平均数，选择“好情境”“好问题”十分重要。上述教学中，教者有意拉长了“用平均数代表一组数据的整体水平”这一认知过程。首先是从欢欢和乐乐的记数成绩入手，引出“谁的记数水平高”的真实问题，进而引导学生借助直观图，讨论、辨析“用哪个数代表这组数据的整体水平更合理、更公平”。在对比分析、辨析研讨的过程中，学生对平均数的代表性有了深刻体会。

师：有同学是用算式（5+4+7+5+9）÷5求出平均数的，这个算式里有没有体现“移多补少”呢？能借助这个图来解释一下吗？

生1：5+4+7+5+9是求一共有多少个圆圈，除以5就是把这些圆圈平均分成5份，也就是把5次的数据都变得一样多。

师：把欢欢5次记数的成绩加在一起就代表“总数”，也就是“整体”，除以次数就代表“平均”，这样就得到了平均数“6”。

【思考】让学生借助直观图解释算式的意义，不仅帮助学生理解“先求和再平均”的计算方法，也能加深学生对平均数的意义的理解。

3. 环节三：借助直观，感受平均数的特征

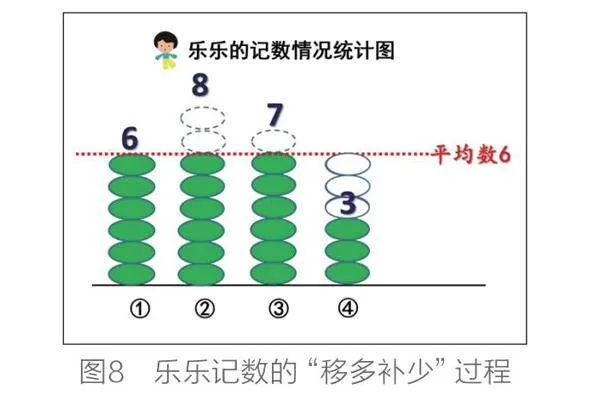
教师出示课件，动态呈现乐乐4次记数“移多补少”的过程，得出乐乐记数的平均数（见图8）。

师：仔细观察这幅图，你还有什么发现？

生1：我发现比平均数多的有3个，比平均数少的也有3个。

师：你知道为什么会这样吗？

生1：因为从多的移走的3个都补给了少的。

生2：我发现平均数比最大数小，比最小数大。

生3：我也发现了！我还知道为什么，因为如果是最大数，就要为整体“做贡献”，移走一部分给小的数；如果是最小数，大的数就会补给它。

师：你们不仅发现了平均数是一个“不大不小的数”，还讲出了道理，真的很棒！想一想，如果乐乐再玩第五次游戏，你觉得这5次记数的平均数跟原来4次的平均数6相比，会有变化吗？如果有变化，又会怎么变呢？

学生小组讨论，全班交流。

生1：如果第五次记住的数比6大，平均数会变大；如果第五次记住的数比6小，平均数会变小；如果第五次记住的数是6，平均数就不会变。

生2：我能解释道理，因为按照“移多补少”的方法，如果第五次的数比6大，就要从这个数中移走一些补给小的数，就会拉高平均数；如果第五次的数比6小，平均数6就会补给它，就会拉低平均数；如果第五次恰好是6，就不用“移多补少”，平均数就不会变。

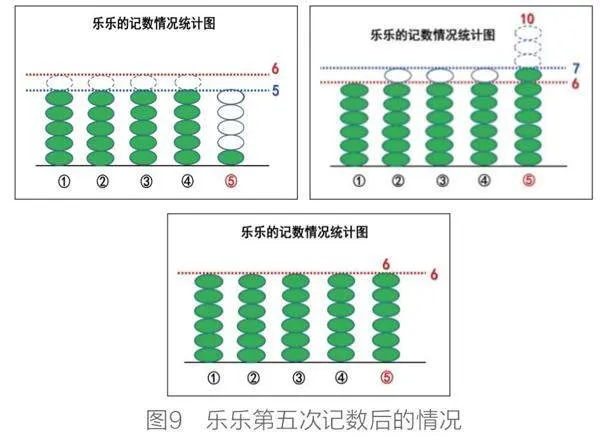
教师逐一呈现乐乐第五次的记数情况（见图9）：分别记住了1个、10个和6个，动态呈现“移多补少”的过程，验证学生的猜想。

师：通过观察，你有什么新发现吗？

生1：我发现只要一个数变了，平均数就会变。

师：你真善于观察！平均数很敏感，任何一个数据变化都会引起平均数的变化。给大家讲一个真实的故事《埃蒙斯的最后一枪》。2008年北京奥运会射击比赛中，美国选手埃蒙斯前9枪的平均成绩是10.1环，大比分领先第二名。但是，埃蒙斯的最后一枪只打出了4.4环，导致10枪的平均成绩仅有9.5环，不仅丢了金牌，连奖牌都没有拿到！听完故事你们有什么感受？

生2：平均数真的很敏感！

师：是的，平均数作为一组数据的代表，跟每一个数据都有关系，如果出现了极端数据，对平均数的影响是非常大的！

【思考】借助几何直观模型和生活事例，让学生真切地体验到平均数“很敏感”，易受极端数据的影响。

4. 环节四：走进生活，应用平均数

（1）计算自己记数的平均数，感受平均数可以是小数

师：算一算，你三次记数的平均成绩是多少呢？

学生独立计算，全班交流，发现有的算式得不到整数结果，平均数可以用小数表示。

【思考】学生三次记数的数据都是随机数据，即同一事件在不同时间点测量所获得的数据。学生通过计算，不仅能更深刻地体会“平均数不是客观存在的，而是通过加工原始数据得到的”，而且能初步感悟平均数的“随机性”。

（2）生活中的平均数

教师出示数据（见图10）：2020年，北京市把儿童乘车免票身高由1.2米提高至1.3米。

师：你认为免票线提高的主要原因是什么？为什么要提高到1.3米而不是其他高度呢？

生1：因为北京市儿童平均身高上升了。

生2：1.3米可能是北京市儿童身高的平均数。

生3：大多数北京市儿童的身高都已经1.3米了。

师：这个1.3米实际上是学龄前儿童的平均身高，这个数据是通过抽样调查统计得来的。

【思考】让学生感受到平均数在生活中应用的广泛性，知道生活中的平均数是通过抽样调查得到的，进一步体会平均数的价值。

（作者系北京亦庄实验小学教师，正高级教师，北京市特级教师）

责任编辑：孙昕