基于二重故障区间定位和随机森林算法的锂电池组突发性故障诊断
2024-11-09申晓伟伦淑娴任冬
摘 要:锂电池的突发性故障往往会在短时间内造成极大的危害,制约其进一步的发展。因此,本文对突发性故障进行研究,提出了一个完整的锂电池组突发性故障诊断框架。首先,利用经验模态分解(EMD)对电压数据序列进行分解,将子序列构建新的数据序列并导入二重故障区间定位模型中,利用二分法思想的相关系数和基于时间窗的相关系数诊断突发性故障的故障区间。然后,利用核主成分分析法提取故障特征。最后,使用随机森林算法对故障进行训练和分类,并且与其余方法进行比较。此外,建立故障注入平台,以物理方式触发串联4节电池组上的外部短路和接触故障。试验结果表明,该方法对突发性故障的诊断准确可靠。
关键词:锂电池; 突发性故障诊断; 二重故障区间定位; 数据提取; 随机森林算法
中图分类号:TM912 文献标识码:A DOI:10.19452/j.issn1007-5453.2024.07.003
基金项目: 国家自然科学基金(61773074);辽宁省教育厅重点攻关项目(LJKZZ20220118)
随着锂电池制造技术的发展进步,锂电池凭借大容量、大放电倍率、小体积、易组合等优点被广泛使用,在航空航天、电动汽车和移动终端等领域都得到大规模应用。在航天领域中,锂电池在飞行器应急电源、储能装置、能源中间转换装置等方面应用广泛。锂电池在使用过程中通常采用串联和并联相结合的方式组合成锂电池组来满足工作的要求电压和续航时间,而锂电池组的复杂结构会增加故障发生的概率。此外,与锂电池普遍使用的程度相比,锂电池的故障诊断研究还处于相对落后的阶段[1-3]。
目前锂电池的故障分为突发性故障和持续性故障两大类。锂电池的突发性故障包括外部短路故障和连接松动故障。开路故障是连接松动故障最严重的表现形式,同时也是危害性较大的故障之一,突发性故障是指由于某种情况导致锂电池瞬间发生的故障,并且在短时间内就导致锂电池无法工作,引发严重的后果。持续性故障包括过度充电故障、过度放电故障、内部短路故障等。持续性故障是指锂电池发生该类故障后,可以在一定时间内持续工作,暂时不会造成锂电池失控。从结果来看,突发性故障发生时间短,危害性大,因此本文对突发性故障进行研究。
近几年锂电池组的安全问题受到广泛的关注,业内提出了多种检测突发性故障的方法。这些方法大致可以分为基于模型的诊断方法和基于数据驱动的方法两类。
基于模型的故障诊断方法通常是建立锂电池的等效电路模型或者电化学模型来模拟锂电池的工作过程,分析模型的状态和参数来检测锂电池的故障。陈泽宇等[4]使用一阶电阻-电容电路模型来模拟外部短路故障过程中锂电池的状态,结合动态邻域粒子群算法识别模型参数,并且提出一种双重模型的外部短路诊断算法,第一层通过参数阀值粗略判断是否存在异常情况,第二层对可疑数据进行精确判断。于全庆等[5]建立多种锂电池的拓扑结构模型并且加入初始荷电状态作为参数变量来诊断外部短路故障。熊瑞等[6-7]建立两步等效电路模型,并提出了一种基于在线模型的电池组外部短路故障诊断方案。
基于数据驱动的诊断方法主要利用的是电池管理系统的实时数据对电池故障进行判断分类。夏冰等[8-9]提出基于递归移动时间窗的电压相关系数法用来判断识别电池外部短路故障,为了解决电池不一致性的问题,提出一种新c7dd94feb6817d6679179cfb34d9cba2181dcd68d1345363de337d9c36344cd8的测量电池电压的拓扑结构,并且通过设定的阀值与不同电池之间的相关系数比较来判别电池故障。康永哲等[10-11]针对电池组中电池之间的不一致性提出了交叉测量拓扑结构,利用改进的相关系数方法和设定的阀值进行比较,实现对外部短路故障的诊断。杨毅拼等[12]在利用交叉测量拓扑结构和相关系数法确定故障区间后,使用小波分解和主成分分析法来进行数据特征提取,最后利用相关性向量机来实现电池外部短路故障的分类。
基于前人的研究,本文结合二重故障区间定位方法和随机森林算法提出一种新的突发性故障诊断方法,本文建立了一个故障注入平台来模拟突发性故障,收集真实的故障数据集;使用二重故障区间定位模型,提高对突发性故障的故障定位效率;建立了一套完整的锂电池组突发性故障诊断框架,提高了诊断成功率。
1 突发性故障分析
在实际使用过程中,引发锂电池产生故障的原因有多种,而不同的故障原因引发的故障类型也不同。锂电池的外部短路故障和接触故障属于突发性故障。这种故障的发生一般是因为外部环境或使用条件突然改变,导致锂电池内部的反应不可逆转而发生的。例如,短路故障可能是因为电池外部受到损坏或火灾等因素导致,而接触故障可能是因为连接器等部件松脱、氧化等原因导致。
本文重点探讨锂电池的突发性故障的原因与表现状况。表1是对锂电池突发性障碍的情况进行的说明。

2 数据预处理
2.1 经验模态分解方法
锂电池的电压数据是一个复杂的波动信号,并且由于信号漂移或者仪器漂移等因素导致的电压数据中出现趋势项,趋势项会隐藏在电池的老化状态和电池之间的不一致性中。这会大大影响对电压数据的分析。经验模态分解方法被黄锷等[13]提出来解决信号数据的趋势项问题,作为一种时频域信号处理方式,经验模态分解方法(EMD)实质上是对非平稳信号进行平稳化处理的一种手段。其将信号中不同尺度的波动和趋势进行逐级分解,产生一系列具有不同特征尺度的数据序列,该数据序列被称为固有模态函数(IMF)。IMF必须同时满足两个条件:(1)整个数据中极值点和过零点的数目必须相等或至多相差一个;(2)在研究对象的时域中,由三次样条插值法拟合最大值和最小值点确定的上、下包络线的平均值是0。


2.3 基于二分法和相关系数的故障区间定位
在长期的运行测试试验中,大量的电池组测试数据被累积,但电池组中的突发性故障会在极短的时间内发生,并且导致故障电池的健康情况迅速恶化。所以从大量测试数据中定位到故障区间是检测突发性故障的关键。二分法是一种常见的搜索算法,其在大量数据中查找数据的效率极高。每次比较时都将查找区域减半,因此可以快速地定位目标。将二分法思想与相关系数法相结合,对锂电池的测试数据进行检测,实现对故障区间的快速定位。
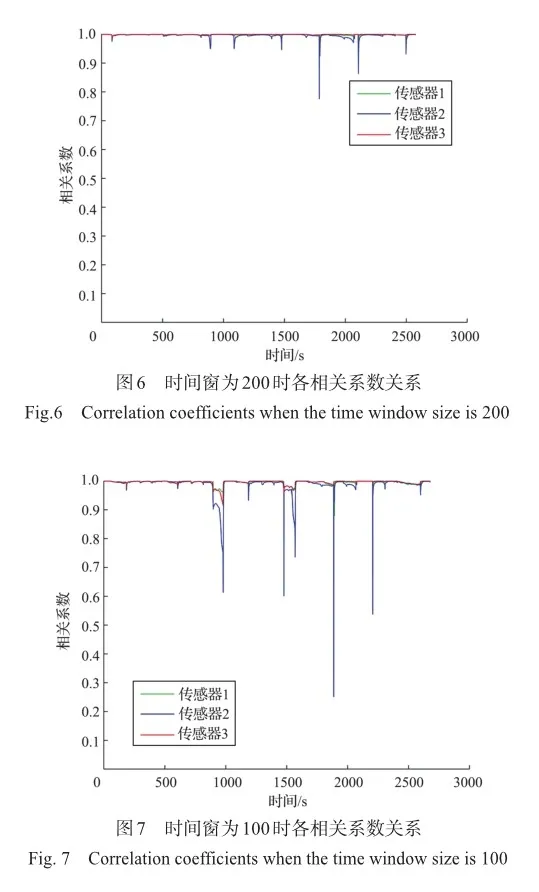
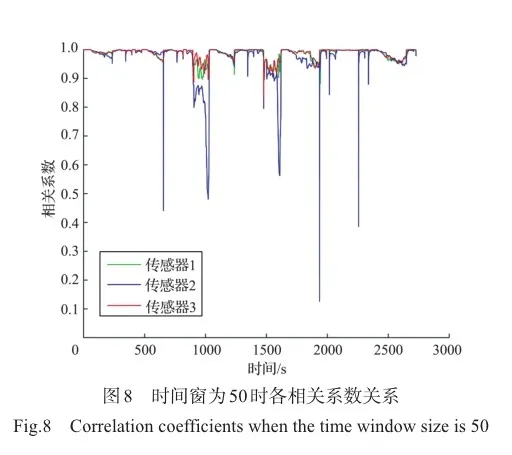
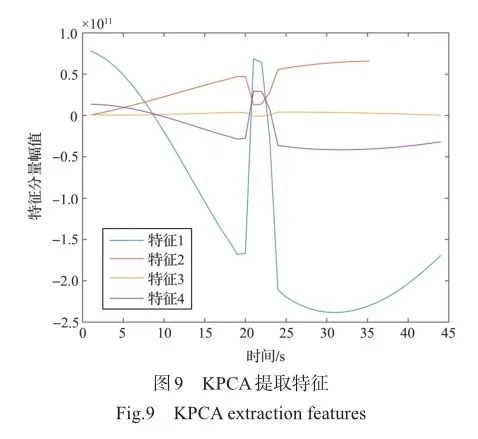
2.4 基于时间窗和相关系数的故障区间定位
时间窗常被用在数据分割当中,小的时间窗使得相关系数对异常数据非常敏感,微小电压变化会导致相关系数大幅波动,容易出现故障误诊。较大的时间窗使得相关系数难以区分故障信息和电压数据值,导致故障检测困难。对于使用二分法无法区分故障区间的接触故障数据和正常数据,采用时间窗的方法来划分数据,依次计算每个时间窗的相关系数,用来诊断接触故障的故障区间。
3 特征提取与分类
3.1 核主成分分析法
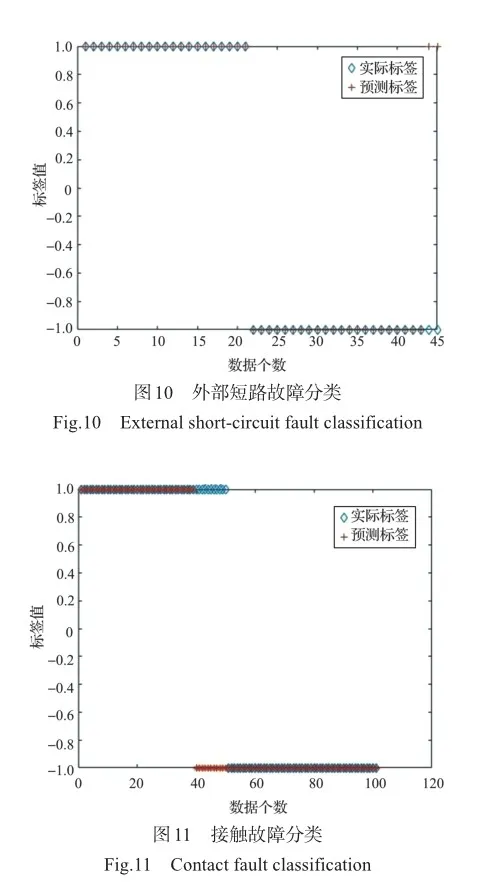
核主成分分析法(KPCA)是主成分分析法(PCA)在非线性系统中的扩展应用。KPCA与PCA的原理类似,都是将数据降维处理后,根据贡献度来选择主元素。但不同的是PCA是一种线性变换,在线性系统中使用。而KPCA适用于非线性系统,通过非线性映射函数将低维空间的处理数据映射到高维空间当中,并且在高维空间实现数据降维。在本文设计中KPCA选择的核函数为径向基核函数,并且利用KPCA提取故障区间包含的IMF分量的数据特征。
3.2 随机森林算法
决策树是普遍使用的一种树状分类器,其是随机森林算法的基分类器。决策树通过在树的每个节点测试样本的属性来对样本进行分类。每个节点测试一个特定的属性,树的叶子代表输出标签。向下移动树的特定分支测试每个节点的特定属性,以便到达输出标签。基于基尼系数分裂的CART准则被用来构建决策树,在树的节点计算属性划分形成的两个子集的基尼系数,并且选择其中较小的属性将节点分成两个子节点,通过不断计算属性的基尼系数值,最终得到完整的决策树。
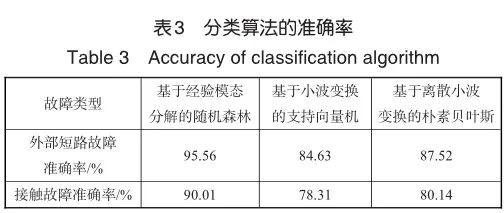
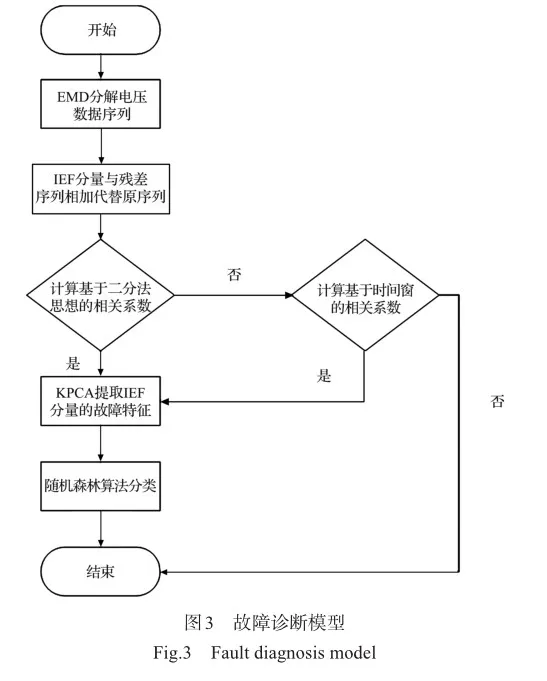
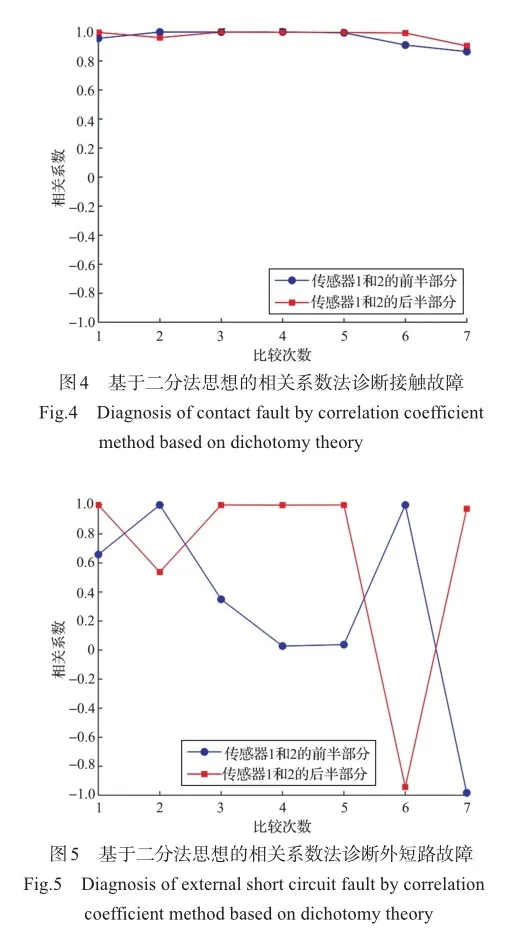
考虑到单决策树本身性能的限制,由许多独立决策树组成的随机森林算法被Breiman提出,其是基于自助聚合(Bagging)并行式集成学习框架的基础上改进而来。在随机森林中,将原始数据中随机均匀采样得到的数据集作为基分类器输入,所以经过训练的基分类器之间是相互独立的关系。随机森林主要由三部分组成:样本采集部分、随机属性子空间选择部分和投票部分。样本采集部分是在构造决策树作为基分类器时,必须有放回的随机抽取同等数量的多个数据点作为采样数据。随机属性子空间选择部分是指决策树的构建过程。在采样数据集的基础上使用基尼系数分裂的CART准则构建决策树。从采样数据集的m个原始属性中随机抽取n个属性(n 4 试验验证和分析 4.1 试验对象 本文使用4块锂电池串联搭建试验平台,通过故障注入平台为锂电池注入不同类型的突SWfnuuTuUXqi1trCDHCpBQ==发性故障,并且采集锂电池的电压数据。 本文使用锂电池型号为656090-5000mAh,其具体参数见表2。 4.2 故障注入平台 故障注入平台由数据采集板、电池测试系统、故障注入装置和数据处理器4种部件组成。4节锂电池组成一个串联电池组。级间传感器的拓扑结构如图1所示,用于测量4个串联电池的电压。试验平台如图2所示,电池测试系统在室温下对试验电池组单元动态执行应力测试(DST)工步。第一台电池检测系统型号为C1-4001-60V100A-NA,其执行DST工步,对电池组进行充电和放电,第二台电池检测系统型号为C1-8004-5V200A-NIFA,其收集电池组的电压数据,其采样频率为10Hz,电压范围为0~5V。故障注入装置由STM32F103RCT6微处理器、继电器等组成。 由于发生外部短路故障时,电池的电压和电流都发生剧烈变化,极易引发热失控等严重后果,因此外部短路故障的持续时间是以毫秒为单位。选择10mΩ的金属电阻作为短路电阻并联在试验电池两端,故障时间分别为100ms、300ms和500ms。根据故障时间的不同,分为三组试验,每组试验次数为10次。 接触故障的故障表现与外部短路故障不同,接触故障会导致增大的电池组性能下降或失效。因此,选择1Ω、2Ω和5Ω的金属电阻与试验电池串联。根据串联金属电阻阻值的不同,分为三组试验,每组试验次数为10次。 4.3 建立故障诊断模型 根据试验设计,使用4块锂电池组成的串联电池组模拟突发性故障,并且记录试验数据。本试验的电压数据分为外部短路故障数据、接触故障数据和正常数据三种。首先,利用EMD对得到的试验数据进行分解,使用得到的IMF分量和残差重新构建对应的试验数据,由于外部短路故障的数据跟正常数据和连接松动故障数据有明显区别,所以利用二分法结合相关系数来构成第一重故障区间定位模型,用于迅速判别外部短路故障区间。而正常数据和连接松动故障数据类似,因此利用时间窗和相关系数来构建第二重故障区间定位模型,用于判别连接松动故障区间。之后,使用KPCA对IMF分量数据提取数据特征,将特征数据输入随机森林算法,最终得到分类结果。该模型工作过程如图3所示。 4.3.1 数据处理和分析 将试验测量得到的电压数据使用EMD进行分解,因为EMD是根据信号的特征时间尺度来识别信号中所内含的所有振动模态进而分解得到IMF分量,所以每组电压数据分解得到IMF分量的数量不一定相同。因此采取4组IMF分量中最少的一组IMF分量个数作为数量标准。之后将分解得到的IMF分量和残差依次相加得到新的数据序列。由基于二分法思想的相关系数和基于时间窗的相关系数法组成的二重故障区间定位对新的数据序列进行识别判断。 如图4和图5所示,外部短路故障数据有明显的异常波动,而接触故障数据和正常数据没有明显的异常波动。基于二分法思想的相关系数法能迅速识别有明显波动的外部短路故障数据,同时利用二分法逐次划分的数据区间,逐渐接近故障区间,直到最后一次比较得到相关系数小的数据区间即为故障区间,实现了故障定位。 如图6~图8所示,接触故障数据和正常数据由基于时间窗的相关系数法区分识别,当相关系数值下降,则说明该时间窗存在故障导致电压数据波动。时间窗长度的选择会直接影响相关系数法的灵敏度,当时间窗长度较小时,对电压变化比较敏感,电压数据采集中的噪声会对诊断结果造成较大影响;当时间窗长度较大时,对电压变化比较迟钝,容易忽视故障导致的电压变化。此外,在试验电池组的初始状态基本一致的前提下,时间窗的选择会放大电池之间的不一致性,导致相关系数出现波动,但与接触故障的相关系数相比,其波动属于小范围的正常波动。接触故障的相关系数随着电池检测系统的试验工步变化,波动更加明显。 4.3.2 特征提取 通过二重故障区间定位的方法可以将数据进行简单分类,并且确定故障数据的区间。然后KPCA将EMD分解得到IMF分量按照贡献度提取故障特征。如图9所示,通过预先设定的参数,选取贡献度最大的前4组特征值作为数据特征输入随机森林算法中,实现故障分类。 4.3.3 故障分类 任选两个故障的试验数据进行分类,并且将经过KPCA处理之后的数据特征输入随机森林算法。 如图10所示,本次测试集有45个数据,只有第44个数据和第45个数据的标签值被错误分类,其余数据均能实现正确分类,分类的准确率较高。由此可以证明,该方法能够有效检测出异常数据,判定出对应的锂电池故障,实现故障检测。 如图11所示,本次测试集有101个数据,第40~50个数据的标签值被错误分类。由于接触故障本身的特点,该分类的准确率可以被接受。由此可以证明,该方法能够有效检测出异常数据,判定出对应的锂电池故障,实现故障检测。 4.4 模型对比分析 本文设计的模型分类的结果见表3,在本次试验中,将多次分类结果准确率的平均值作为最终的准确率,随机森林分类得到的外部短路故障的准确率为95.56%,接触故障的准确率为90.01%,而基于小波变换的支持向量机和基于离散小波变换的朴素贝叶斯两种方法的外部短路故障分类准确率分别是84.63%和87.52%,接触故障的准确率分别是78.31%和86.14%,说明选择二重故障区间定位和随机森林算法具有合理性。 5 结束语 锂电池的突发性故障具有时间短、危害性大的特点,针对该类故障,本文提出了二重诊断故障区间的定位模型,通过EMD对原数据序列进行分解,基于二分法思想的相关系数和基于时间窗的相关系数分别作为诊断故障区间的依据,利用KPCA对提取高贡献度的故障特征,最后使用随机森林对故障类型进行分类。试验分析验证了该方法对突发性故障具有很好的识别效果。下一步将重点研究持续性故障的原因和故障特点,提出对应的诊断方法。 参考文献 [1]王海斌, 王茂华, 郑永军.航空用动力锂电池组工作特征的研究[J].太原学院学报(自然科学版), 2021, 39(1): 35-39. Wang Haibin, Wang Maohua, Zheng Yongjun. Study on operating characteristics of power lithium battery pack for aviation [J]. Journal of Taiyuan University (Natural Science Edition), 2021, 39(1): 35-39. (in Chinese) [2]何振亚, 唐兴中.电动直升机关键性能指标及影响因素研究[J].航空科学技术, 2023, 34(3): 16-24. He Zhenya, Tang Xingzhong.Research on key performance in‐dex and influencing factors of electric helicopter [J]. Aeronauti‐cal Science & Technology, 2023, 34 (3):16-24. (in Chinese) [3]艾凤明,梁兴壮,董润,等.军用飞机供配电系统故障预测与健康管理关键技术[J].航空科学技术,2023,34(2):86-95. Ai Fengming, Liang Xingzhuang, Dong Run, et al. Key technologies of fault prediction and health management for military aircraft power supply and distribution system [J]. Aeronautical Science & Technology, 2023, 34 (2):86-95. (in Chinese) [4]陈泽宇, 熊瑞, 孙逢春.电动汽车电池安全事故分析与研究现状[J].机械工程学报, 2019, 55(24): 93-104+116. Chen Zeyu, Xiong Rui, Sun Fengchun. Analysis and research status of electric vehicle battery safety accidents [J]. Journal of Mechanical Engineering, 2019, 55(24): 93-104+116. (in Chinese) [5]于全庆, 王灿, 李建明,等.多拓扑结构锂电池组外短路特性分析及模型评价[J].机械工程学报, 2023, 59(6):159-172. Yu Quanqing, Wang Can, Li Jianming, et al. Analysis of external short-circuit characteristics and model evaluation of multi-topology lithium battery pack [J]. Chinese Journal of Mechanical Engineering, 2023, 59(6): 159-172. (in Chinese) [6]Chen Zeyu, Xiong Rui, Tian Jinpeng,et al. Model-based fault diagnosis approach on external short circuit of lithium-ion battery used in electric vehicles[J]. Applied Energy,2016,184:365-374. [7]Xiong Rui, Yang Ruixin, Chen Zeyu, et al. Online fault diagnosis of external short circuit for lithium-ion battery pack[J]. IEEE Transactions on Industrial Electronics,2020,67(2):1081-1091. [8]Xia Bing, Nguyen T, Yang Jufeng, et al. The improved interleaved voltage measurement method for series connected battery packs [J]. Journal of Power Sources, 2016, 334: 12-22. [9]Xia Bing, Shang Yunlong, Nguyen T, et al. A correlation based fault detection method for short circuits in battery packs [J]. Journal of Power Sources, 2017, 337: 1-10. [10]Kang Yongzhe, Duan Bin, Zhou Zhongkai, et al. Online multifault detection and diagnosis for battery packs in electric vehicles[J]. Applied Energy, 2020, 259: 114170. [11]Kang Yongzhe, Duan Bin, Zhou Zhongkai, et al. A multi-fault diagnostic method based on an interleaved voltage measurement topology for series connected battery packs [J]. Journal of Power Sources, 2019, 417: 132-144. [12]Yang Yipin, Lun Shuxian, Xie Jiale. Multi-fault diagnosis for battery pack based on adaptive correlation sequence and sparse classification model [J]. Journal of Energy Storage, 2022, 46: 103889. [13]Huang Er, Zheng Shen, Steven R L, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995. Sudden Fault Diagnosis of Lithium Battery Pack Based on Double Fault Interval Location and Random Forest Algorithm Shen Xiaowei, Lun Shuxian, Ren Dong Bohai University, Jinzhou 121013, China Abstract: Sudden faults of lithium batteries often cause great harm in a short period of time, restricting theiL6/5N9ieidoJ+PMLcnYA1Q==r further development. Therefore, this paper investigates sudden faults and proposes a complete framework for diagnosing sudden faults in lithium battery packs. First, the voltage data sequence is decomposed using empirical modal decomposition, and the subsequence is constructed into a new data sequence and imported into the binary fault interval localization model, and the correlation coefficient of dichotomous ideas and the correlation coefficient based on the time window are used to diagnose the fault interval of the sudden fault. Then, the fault features are extracted using kernel principal component analysis. Finally, the faults are trained and classified using the random forest algorithm and compared with the remaining methods. In addition, a fault injection platform is established to physically trigger external short circuit faults and contact faults on a series-connected four-cell battery pack. The experimental results show that the method is accurate and reliable for the diagnosis of sudden faults. Key Words: lithium battery; sudden fault diagnosis; double fault interval location; data extraction; random forest algorithm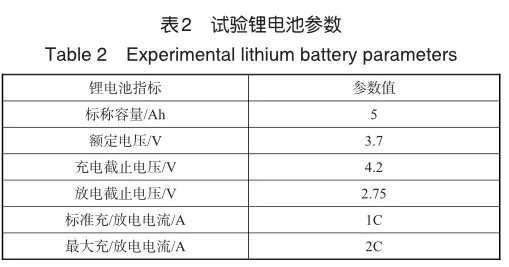

 Peb6iblbBcL9IuzMXWcH6Q==
Peb6iblbBcL9IuzMXWcH6Q==