基于重抽样加权的飞行器多源数据融合方法

摘 要：风洞试验方法和计算流体力学（CFD）数值模拟方法在飞行器的初步研制阶段能够对于飞行器的气动性能提供精准分析，其对于飞行器的气动外形优化与设计起到了重要的作用。而风洞试验与CFD方法不可避免地存在试验与计算成本较高等问题。为实现对于飞行器气动性能的低成本及高效分析，本文对风洞试验数据进行了机器学习方法的预测分析研究，提出了一种基于多模型结合方法的数据融合模式，其原理是通过重复抽样的方法多次获取精度略低的CFD数据与精度较高的风洞试验数据之间的映射关系，并通过基于均方误差的加权方法对于多映射关系进行结合从而输出最终的预测结果。结果表明，基于重抽样加权法的数据融合模式可以有效提升风洞试验数据预测的精准度与拟合度，辅助支撑风洞试验人员进行相关研究工作。

关键词：数据融合； 重抽样加权法； 风洞试验； CFD； 机器学习

中图分类号：V211.3 文献标识码：A DOI：10.19452/j.issn1007-5453.2024.07.012

基金项目： 航空科学基金（2022Z006026004，2023M071027001）

在飞行器的初步研制阶段，根据飞行器的气动外形需要开展相对应的气动数值计算和气动特性评估，以规划进一步地优化设计方案，因此对于飞行器气动外形进行精准且高效分析是必要的[1-3]。目前风洞试验和计算流体力学（CFD）数值模拟是面向飞行器的气动特性分析的主要技术方法[4]。风洞试验能够对飞行器的气动外形开展精准度较高的气动特性分析，但是存在成本高、试验周期过长等问题。CFD方法采用数值计算对于流体力学中的离散方程进行求解，与风洞试验相比，CFD方法在成本上有所下降，但是在精度上却略低于风洞试验结果[5-7]。

针对风洞试验和CFD数值模拟存在的弊端，需要在合理发挥自身优势的基础上，进一步研发出一种既满足低试验成本又能够获取高精度数据分析结果的方法。为此，一种基于多源气动数据融合的理念在国内外被广泛研究与应用，其本质是采用了一种能够映射出低精度数据与高精度数据之间关系的代理模型，并实现对于高精度数据的精准预测。目前为止，国内外对于多源气动数据融合所开展的研究工作已经取得了一些突破性的进展，王文正等[8]首次提出了一种基于数学模型的多源气动数据融合准则，并证明该方法的可行性；He Lei等[9]采用了一种深度神经网络算法（DNN）对于多源气动数据进行预测分析，其提出的气动数据融合模型架构发挥出了良好的预测效果；邓晨等[10]提出了一种加权融合后的高斯过程回归算法，并与地质统计学中的协同克里金法（CoKriging）算法对多源气动数据进行融合，结果表明CoKriging算法预测精度更高；王旭等[11]通过随机森林算法中节点纯净度的特征选择方法对变量特征进行筛选，保留低精度数据变量特征及其他重要的变量特征，结果表明该方法具备良好的精准度和拟合度；赵旋等[12]基于本征正交分解技术（POD）对于压力分布信息进行特征提取并生成POD系数，对输入参数与POD系数之间采用克里金（Kriging）模型进行建模分析，并通过积分得到低精度数据，最后通过Kriging模型获取低精度数据与高精度数据之间的映射关系，结果表明该方法具有良好的精准度和泛化能力。

上述文献通过不同的代理模型有效获取了高低精度数据之间的映射关系，提出的多源气动数据融合方法在预测精度上有所提升，但目前所涉及的方法均使用固定训练集与测试集的单次建模得到单一的高低精度数据之间的映射关系，当数据较少时，容易发生过拟合的情况，为进一步提升预测结果的精准度与拟合度，本文提出一种多模型结合的方法。根据辛钦（Khinchine’s）大数定律和中心极限定理，当样本之间是独立分布时，数量足够多的样本数据的平均值将近似等于总体数据的平均值[13-14]。基于上述数理推论，如若将代理模型在不同训练集下所得出的映射关系进行均值或加权融合，最终预测结果将可能更加接近于真实值。因此，本文提出了一种基于重抽样加权的多模型结合方法，将选取的每种代理模型通过重复抽样法形成多个模型结果，从而获取低精度数据与高精度数据之间的多映射关系，进一步采用一种基于均方误差的加权方法将多模型的映射关系进行融合，最终所得出的结果与单次建模结果相比在精准度和拟合度上均有所提升，结果证明了该方法的可行性和有效性。

1 代理模型选取

在多模型结合方法中，代理模型需要分别在低精度与高精度数据之间建立一种映射关系，映射关系的优劣直接决定了最终数据融合方案的可行性，因此首先要解决的问题是代理模型的选取。本文采用了基于正则化的多种线性回归模型与决策树拟合的多种非线性回归模型，通过不同的代理模型对基于数据融合模式下的预测效果进行验证与比较。本节将对参与试验中的代理模型进行逐一解释说明。

1.1 基于正则化的线性回归模型

在基于函数拟合的回归模型中，最具有代表性的则是线性回归模型，其通过在输入变量和输出变量之间构建函数关系从而进行预测分析。线性回归算法具有易于实现、可解释性高的特点[15]。但是在训练集较少时，线性回归方法会面临模型过度拟合的问题[16]。为了避免这种情况发生，对于线性回归模型需要采取必要的正则化处理。正则化是机器学习中的一项优化技术，其具备增强模型泛化能力的特征。正则化通过在损失函数的基础上加入惩罚项使得权重系数（回归系数）下降以降低模型复杂程度，可以在一定程度上避免过度拟合并减少模型的方差[17]。基于正则化的线性回归方法主要有Lasso回归法、Ridge回归法、ElasticNet回归法，三种方法通过采用不同的惩罚项表达方式进行正则化处理[18-20]。

1.2 基于决策树的集成回归模型

决策树是一种基于树形结构的机器学习模型，由决策节点、分支和叶节点组合而成。其中决策节点表示数据集的特征，分支表示决策规则，每个叶节点表示决策输出结果。决策树具有可解释性高的优势，其可视化的树状结构易于理解和分析[22]。同时，决策树具有非参数化的特征，因此不需要考虑数据预处理阶段中的数据转换和缺失值填补等问题[23]。然而，有时决策树算法会根据训练集的情况产生深度较大的复杂结构从而导致模型出现过度拟合的问题[24]。针对此类问题，基于决策树的集成方法通过将多个决策树进行融合，一定程度上能够缓解模型过度拟合的弊端[25]。Random Forest方法和AdaBoost方法作为决策树的集成模型中具有代表性的算法，本文对两种算法分别进行应用。

1.2.1 Random Forest方法

Random Forest方法通过有放回的随机抽样方式提取多个训练集从而形成多个决策树模型，对于每个决策树模型分别根据信息增益或基尼系数进行有效分裂，最终将多个决策树组合成为随机森林，如若是分类问题，则通过投票方式决定预测结果；如若是回归问题，则通常通过均值方式获取预测结果。Random Forest方法结合多个决策树的结果，不仅在精准度上有所提升，也一定程度上避免了模型过度拟和的问题[26]。与有放回的随机抽样方式提取训练集不同的是，本文采用一种无放回的子样本抽样方式进行训练集选取，文献[27]中证明了该方法的可行性。

1.2.2 AdaBoost方法

AdaBoost方法与Random Forest方法具有相同的优势，其在精准度上有所提升且可以缓解模型过度拟和的问题。两者的区别是，AdaBoost方法的决策树之间相对依赖，而Random Forest方法生成的决策树之间则相对独立[29]。

2 重抽样加权法

多模型结合方法需要进一步解决的问题在于如何通过代理模型进行多次训练建模，并对于多模型的预测结果进行有效结合。本文将采用重复抽样法（RSM）形成多模型结构，重复抽样法是统计学方法中常用于通过样本来评估总体的方法，其原理是将样本数据进行多次无放回的随机抽样，并将抽样到的样本组成训练集、将未抽样到的样本组成检验集，并基于不同的训练集分别建立模型从而形成多模型[30]。在多模型的基础上，进一步对每个模型分配对应的权重来得到最终的预测结果。其中最直接的方法则是采用重抽样平均法，通过将重复抽样方法产生的模型赋予相同权重的方式从而结合得出最终结果。

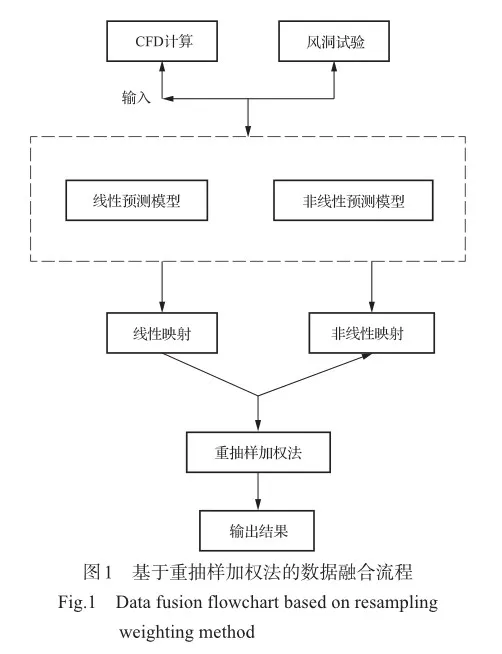
图1展示了基于重抽样方法的数据融合流程，其核心原理是通过建立CFD数据与风洞试验数据之间的线性和非线性的映射关系，以重抽样加权方法进行映射结果结合，形成一种合并多种映射关系的数据融合方法。

重抽样加权方法的步骤可以分解为：首先，将数据集划分为训练集与测试集。其次，通过重复抽样法在训练集中抽取部分样本点作为新的训练集，剩余样本点作为新的验证集。再次，使用代理模型对于新的训练集进行建模，通过验证集获取预测结果的均方误差，并记录建模后的模型信息和获取的均方误差。最后，使用多次建模得到的模型信息分别对测试集进行预测，并基于均方误差的加权方法将多模型的预测结果进行结合。

3 试验流程和结果

3.1 数据集介绍

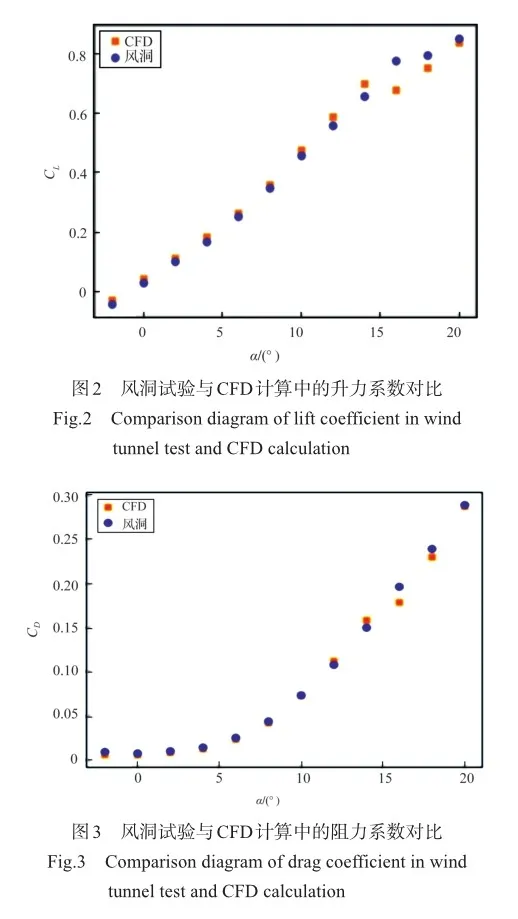
本次试验采用的数据集为某飞翼标模在不同马赫数Ma、迎角α和侧滑角β下通过风洞试验与CFD计算分别得出的升力系数CL与阻力系数CD。数据集中马赫数的取值范围为Ma ={0.6， 0.8， 1.0， 1.2， 2.0}、迎角的取值范围为α={-2°， 0°， 2°， 4°， 6°， 8°， 10°， 12°， 14°， 16°， 18°， 20°}、侧滑角的取值范围为β={0°， 3°， 5°}，本次试验数据集共选取了79个状态点。图2和图3分别展示了试验数据集中不同迎角下的Ma=0.6、β=0的风洞试验与CFD计算的升阻力系数对比图，图中黄色方形点表示CFD计算得到的升阻力系数。蓝色圆形点表示的是风洞试验得到的升阻力系数，从图2和图3可以看出，升力系数的试验段一直持续上升，其试验数据非线性特征不明显，在迎角12°以后的非线性较为明显。阻力系数的试验段在不同迎角下呈现出先略微下降、之后持续上升趋势，组成了非线性试验段。

3.2 试验流程概述

首先，试验使用单次建模分析的方式通过代理模型分别进行单源气动数据预测和多源气动数据预测。在单源气动数据预测中，代理模型将马赫数、迎角和侧滑角作为输入，以风洞试验中升力系数与阻力系数作为输出进行预测分析。在多源气动数据预测中，代理模型将在原特征变量的基础上引入CFD计算出的升力或阻力系数从而建立CFD数据（低精度数据）与风洞试验数据（高精度数据）之间的映射关系，试验将进一步比较单源气动数据预测和多源气动数据预测的精准度和拟合度。

其次，试验将采用多模型加权结合方法对于多源气动数据再次进行预测分析，比较使用普通建模分析、重抽样平均法、重抽样加权法的预测结果的精准度与拟合度。本次试验基于某开发环境下开展，在对于升阻力系数的预测分析中，采用不同迎角下固定马赫数与侧滑角的试验段作为测试集，训练集与测试集的比例近似为8.5∶1.5。

3.3 试验结果分析

试验首先通过代理模型对于单源气动数据预测和多源气动数据预测分别进行建模分析与结果评估，试验的评估方法采用平均绝对误差（MAE）、均方根误差（RMSE）来判断模型结果的精准度，预测结果的误差值越接近于0，则表明精准度越高；采用确定系数（R2）来判断模型预测值与真实值之间的拟和程度，R2值越接近1，说明模型拟合度越高。

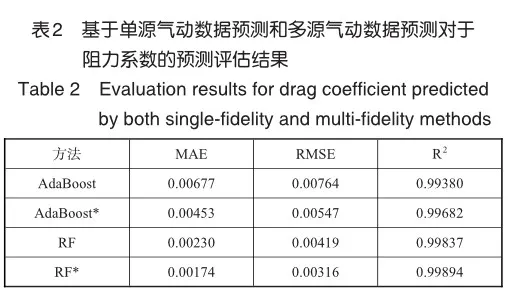
表1展示了各代理模型在数据融合前后的升力系数预测的评估结果对比，表中1的*符号表示代理模型在数据融合后的预测结果。从表1中的结果来看，数据融合后的代理模型对预测升力系数在精准度和拟合度上都有所提升，其中，基于正则化的线性回归方法相比于基于决策树的集成模型在融合后预测效果提升更为明显，但基于决策树的集成模型在预测升力系数上的效果更佳，其中随机森林模型在融合后的精准度和拟合度达到了最优。

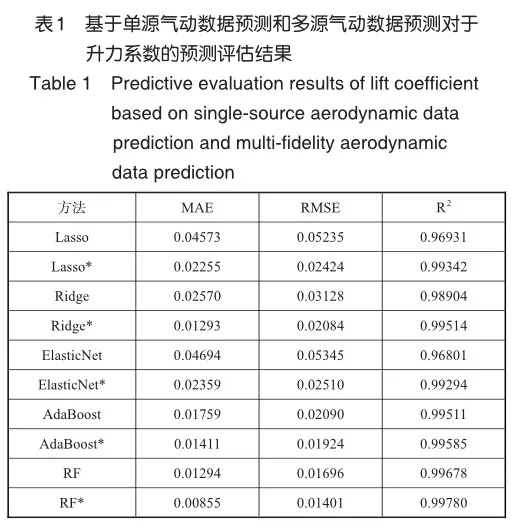
表2展示了各代理模型在数据融合前后的阻力系数预测的评估结果对比。表2中的*符号表示代理模型在数据融合后的预测结果。由于阻力系数在不同迎角下呈现为明显的非线性试验段，因此正则化的线性回归方法并不适用于阻力系数的预测分析，这里采用基于决策树的非线性集成模型对于阻力系数进行预测，其融合后的预测结果在精准度和拟和度上都有所提升，其中随机森林模型在融合后的精准度和拟合度达到了最优。

从表1和表2能够综合得出，多源气动数据预测相较于单源气动数据预测在精准度和拟合度上都有所提高，从而说明数据融合理念的有效性。其中，Random Forest方法相较于其他代理模型在气动数据预测中的效果最为显著。

表3中展示了基于多源数据融合下的多模型结合法的升力预测评估结果对比，表中RSA符号表示重抽样平均法、RSW表示重抽样加权法。同时，试验采取的重复抽样的迭代次数为1000次，但AdaBoost作为一种集成方法无需过大的迭代次数，因此试验为AdaBoost算法设置的迭代次数为500次。重抽样平均法下的决策树算法从本质上与Random Forest方法中无放回的子样本抽样法相同，因此Random Forest在表1中的普通建模方法（RF*）和表3中的重抽样平均法（RFRSA）的预测结果保持一致。表3中采用重抽样加权法下的决策树算法为Random Forest方法（RFRSW）的一种创新形式。

从表1和表3中对比能够得出，基于多源数据融合下的重抽样平均法的精准度与拟合度均略高于表1中的普通建模方法，而重抽样加权法与重抽样平均法相比，预测效果再次得到提升，其中AdaBoost模型在应用重抽样加权法后的精准度和拟合度达到了最优。

表4中展示了基于多源数据融合下的多模型结合法的阻力预测评估结果对比。与表2对应，对于阻力系数的非线性段预测采用基于决策树的非线性集成模型，基于多源数据融合下的多模型平均法在精准度与拟合度上与表2的普通建模方法相比有所提升，重抽样加权法与重抽样平均法相比在预测效果上得到再次提升，其中随机森林模型在应用重抽样加权法后的精准度和拟合度达到了最优。

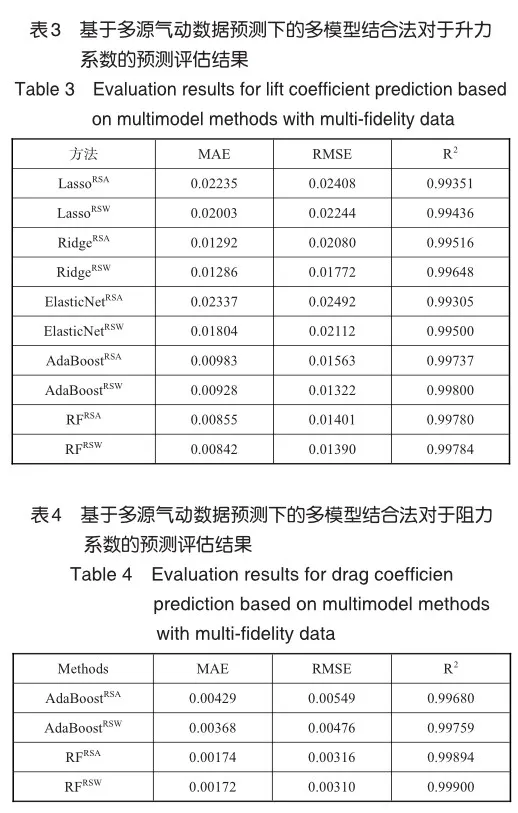
从表3和表4能够综合得出，在多源气动数据预测下的多模型结合法有着良好的性能，其中相比于重抽样平均法，重抽样法的效果更为显著，证明了重抽样加权法能够在传统数据融合方法的基础上再次提升预测结果的精准度与拟合度。

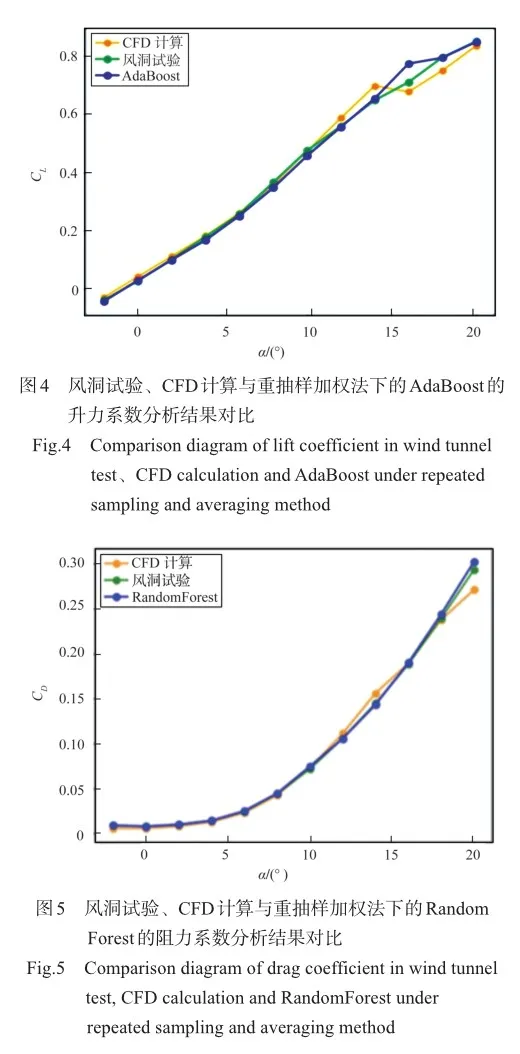
图4和图5分别采用自助抽样法下的最优代理模型对测试集中的升阻力系数进行预测，并与风洞试验、CFD计算结果进行对比。图中黄色曲线代表CFD计算数据、绿色曲线代表风洞试验数据、蓝色曲线代表机器学习预测数据。从图5中能够看出，通过重抽样加权法下代理模型的预测结果与风洞试验结果整体呈现出良好的拟合效果。由此可见，通过重抽样加权法获取到CFD数据与风洞试验数据的多映射关系能够对于风洞试验结果实现精准预测。

4 结论

针对风洞试验方法和CFD方法对于气动力特性分析存在很多局限性问题，本文采用基于数据融合下的多模型结合方法对于气动力的预测分析，得到的结论如下：

（1）通过比较在多种代理模型下单源气动数据预测和多源气动数据预测，试验表明多源气动数据预测具有更高的精准度与拟合度，证明了多源气动数据融合方法的可行性与有效性。

（2）基于多源数据融合下通过对比多模型结合法与单次建模方法的预测结果，试验表明多模型结合法有着更高的精准度与拟合度。同时，在多模型结合法中重抽样加权法的预测效果比重抽样平均法更为显著，证明了基于多源数据融合下重抽样加权法的可行性与有效性。

参考文献

[1]王丹.飞行器气动外形优化设计方法研究与应用[D].西安：西北工业大学， 2015. Wang Dan. Research and application of aerodynamic configura‐tion optimization design method for aircraft [D]. Xi’an： North‐west Polytechnical University， 2015.（in Chinese）

[2]刘济民， 颜仙荣， 张朝阳， 等.高超声速飞机气动外形概念设计[J].航空科学技术， 2022， 33（7）： 15-22. Liu Jimin， Yan Xianrong， Zhang Chaoyang， et al. Conceptual de‐sign of aerodynamic shape for hypersonic aircraft [J]. Aeronauti‐cal Science & Technology， 2022， 33（7）： 15-22.（in Chinese）

[3]项松， 赵伦， 陈虹霖， 等.一种无人机旋翼设计方法[J].航空科学技术， 2022， 33（4）： 1-6. Xiang Song， Zhao Lun， Chen Honglin，et al. A design method for unmanned aerial vehicle rotor [J]. Aeronautical Science & Technology， 2022， 33（4）： 1-6.（in Chinese）

[4]刘小波， 陆韵， 张鑫， 等.基于风洞试验和CFD计算的折叠翼气动特性研究[J].空天防御， 2021， 4（1）：77-82 Liu Xiaobo， Lu Yun， Zhang Xin， et al. Research on aerodynamic characteristics of folding wings based on wind tunnel test and CFD calculation [J]. Aerospace Defense， 2021，4（1）： 77-82.（in Chinese）

[5]DeSpirito J. CFD aerodynamic characterization of 155mm pro‐jectile at high angles-of-a42zYXvVofhyynKZAF/14+w==ttack[C].35th AIAA Applied Aerody‐namics Conference， 2017： 3397.

[6]Antoniou N， Montazeri H， Wigo H， et al. CFD and wind-tunnel analysis of outdoor ventilation in a real compact heterogeneous urban area： Evaluation using “air delay”[J]. Building and Environment， 2017， 126： 355-372.

[7]Blocken B， Stathopoulos T， Van Beeck J. Pedestrian-level wind conditions around buildings： Review of wind-tunnel and CFD techniques and their accuracy for wind comfort assessment[J]. Building and Environment， 2016， 100： 50-81.

[8]王文正， 桂业伟， 何开锋， 等.基于数学模型的气动力数据融合研究[J].空气动力学学报， 2009， 27（5）： 524-528. Wang Wenzheng， Gui Yewei， He Kaifeng， et al. Research on aerodynamic data fusion based on mathematical model [J]. Journal of Aerodynamics， 2009， 27 （5）： 524-528.（in Chinese）

[9]He Lei， Qian Weiqi， Zhao Tun， et al. Multi-fidelity aerodynam‐ic data fusion with a deep neural network modeling method[J]. Entropy， 2020， 22（9）： 1022.

[10]邓晨， 陈功， 王文正， 等.基于不确定度和气动模型的气动数据融合算法[J].空气动力学学报， 2022， 40（4）： 117-123. Deng Chen， Chen Gong， Wang Wenzheng， et al. Aerodynamic da‐ta fusion algorithm based on uncertainty and aerodynamic model[J]. Journal of Aerodynamics， 2022，40（4）： 117-123.（in Chinese）

[11]王旭， 宁晨伽， 王文正， 等.面向飞行试验的多源气动数据智能融合方法[J].空气动力学学报， 2023， 41（2）： 12-20. Wang Xu， Ning Chenjia， Wang Wenzheng， et al. Intelligent fusion method of multi-source aerodynamic data for flight test[J]. Journal of Aerodynamics， 2023， 41（2）： 12-20.（in Chinese）

[12]赵旋，张伟伟，邓子辰.融入压力分布信息的气动力建模方法[J].力学学报，2022，54（9）：2616-2626. Zhao Xuan， Zhang Weiwei， Deng Zichen. Aerodynamic model‐ing method incorporating pressure distribution information [J]. Chinese Journal of Theoretical and Applied Mechanics， 2022，54 （9）： 2616-2626.（in Chinese）

[13]Rosenblatt M. A central limit theorem and a strong mixing condition[J]. Proceedings of the National Academy of Sciences， 1956， 42（1）： 43-47.

[14]Hsu P L， Robbins H. Complete convergence and the law of large numbers[J]. Proceedings of the National Academy of Sciences， 1947， 33（2）： 25-31.

[15]Weisberg S. Applied linear regression[M]. Hoboken： John Wiley & Sons， 2005.

[16]Hawkins D M. The problem of overfitting[J]. Journal of Chemi‐cal Information and Computer Sciences， 2004， 44（1）： 1-12.

[17]Thrampoulidis C， Oymak S， Hassibi B. Regularized linear regression： A precise analysis of the estimation error[C]. Conference on Learning Theory. PMLR， 2015： 1683-1709.

[18]Ranstam J， Cook J A. LASSO regression[J]. Journal of British Surgery， 2018， 105（10）： 1348-1348.

[19]McDonald G C. Ridge regression[J]. Wiley Interdisciplinary Reviews： Computational Statistics， 2009， 1（1）： 93-100.

[20]Zou H， Hastie T. Regularization and variable selection via the elastic net[J]. Journal of the Royal Statistical Society： Series B（Statistical Methodology）， 2005， 67（2）： 301-320.

[21]Ogutu J O， Schulz-Streeck T， Piepho H P. Genomic selection using regularized linear regression models： ridge regression， lasso， elastic net and their extensions[C].BMC Proceedings of BioMed Central， 2012， 6（2）： 1-6.

[22]Myles A J， Feudale R N， Liu Y， et al. An introduction to decision tree modeling[J]. Journal of Chemometrics： A Journal of the Chemometrics Society， 2004， 18（6）： 275-285.

[23]Zhao Yongheng， Zhang Yanxia. Comparison of decision tree methods for finding active objects[J]. Advances in Space Research， 2008， 41（12）： 1955-1959.

[24]Schaffer C. Overfitting avoidance as bias[J]. Machine Learning， 1993， 10（2）： 153-178.

[25]Banf162b3f3ff170e2e12f66a330eff6f398ield R E， Hall L O， Bowyer K W， et al. A comparison of de‐cision tree ensemble creation techniques[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2006， 29（1）： 173-180.

[26]Belgiu M， Dr？gu？ L. Random forest in remote sensing： A review of applications and future directions[J]. ISPRS Journal of Photogrammetry and Remote Sensing， 2016， 114： 24-31.

[27]Strobl C， Boulesteix A L， Zeileis A， et al. Bias in random forest variable importance measures： Illustrations， sources and a solution[J]. BMC Bioinformatics， 2007， 8（1）： 1-21.

[28]Schapire R E. Explaining adaboost[M].Berlin： Springer， 2013.

[29]Cao Ying， Miao Qiguang， Liu Jiachen， et al. Advance and prospects of AdaBoost algorithm[J]. Acta Automatica Sinica， 2013， 39（6）： 745-758.

[30]Soivio A， Nynolm K， Westman K. A technique for repeated sampling of the blood of individual resting fish[J]. Journal of Experimental Biology， 1975， 63（1）： 207-217.

Multi-Fidelity Data Fusion Method for Aircraft based on Resampling and Weighting

Cui Rongfeng， Wang Xiangyun， Liu Zhe， Li Hongyan， Guo Chengpeng

Aviation Key Laboratory of Science and Technology on Aerodynamics of High Speed and High Reynolds Number，AVIC Aerodynamics Research Institute， Shenyang 110034， China

Abstract： The wind tunnel test method and CFD simulation method can provide accurate analysis for the aerodynamic performance in the initial development stage of the aircraft， which plays an important role in the optimization of the aerodynamic shape of the aircraft. However， wind tunnel tests and CFD methods inevitably have the problem of high costs. In order to achieve low cost and efficient analysis on aircraft aerodynamic performance， this paper uses machine learning methods to analyze wind tunnel test data and aims to obtain the relationship between the CFD data with lower accuracy and the wind tunnel test data with higher accuracy through repeated sampling and combine the multiple relationship through the weighted method based on mean square error to obtain the final prediction. The results show that the data fusion mode based on repeated sampling and weighting method can effectively improve the accuracy and goodness of fit of wind tunnel test data prediction.The results demonstrate that the data fusion model based on resampling and weighting can effectively enhance the precision and reliability of wind tunnel test data prediction and assist wind tunnel test personnel to handle relevant research work.

Key Words： data fusion； repeated sampling and weighting method； wind tunnel test； CFD； machine learning