基于二维声学黑洞的周期板结构弯曲波操控特性研究

摘 要：声学黑洞（ABH）结构通过按照一定幂函数剪裁结构厚度，致使结构中弯曲波相速度的减小而实现能量聚集，为航空结构中振动能量操控提供新的思路。ABH阵列可以弥补单个ABH中低频弯曲波操控特性的不足，为了研究基于二维ABH的周期板结构的弯曲波操控特性，利用有限元方法研究无限周期ABH结构的能带结构和包含有限周期ABH的板结构声强矢量场特征，分析了含中心平台ABH与无中心平台ABH构成的周期结构中弯曲波传播特征的区别，结合有限元结果明确了平面波展开方法收敛性和适用条件。数值分析结果显示，含中心平台ABH易在低于全波长特征频率时获得表征局部共振的平直带，从ABH全波长特征频率附近开始，含中心平台ABH周期结构对弯曲波能量的定向操控特征区别于无中心平台ABH周期结构。最后研究ABH截面特征参数对弯曲波能带结构的影响规律，结果表明，内嵌式ABH截面的变化对半波长特征频率附近及低于该频率的弯曲波传播影响比较小，减小中心截断厚度、增大中心平台半径以及幂次大于2有助于形成连续且宽频的方向带隙。

关键词：声学黑洞； 弯曲波； 平面波展开法； 有限元分析； 局部共振

中图分类号：TB123 文献标识码：A DOI：10.19452/j.issn1007-5453.2024.07.010

基金项目： 国家自然科学基金（52022039，U2241261）；航空科学基金（20161552014）

随着科技的发展，航空运载装备对于振动噪声控制标准日渐严苛，对集成度、轻量化以及自适应性有着更高要求，基于材料结构设计不断发展新技术以满足先进装备性能需求成为趋势[1-2]。结构振动源于介质中弹性波的传播，新型弹性波操结构声学黑洞（ABH）主要通过对结构厚度进行裁剪来实现，随着结构厚度的减小，弯曲波波速逐渐减小，波长被压缩，振动幅值增大，振动能量在声学黑洞厚度最薄区域实现能量聚集[3-4]，通过在尖端粘贴少量的阻尼材料可实现对聚集振动能量的高效耗散，达到减振降噪的目的[5-6]。声学黑洞结构相比传统的减振降噪方法具有实现简单、效率高、频带范围宽、轻质的优点，在航空航天装备制造领域有广泛的应用前景。王小东等[7-8]将内嵌式ABH应用于直升机驾驶舱后壁设计，以及交通运输装备中常见的双层壁板结构，通过模拟和试验证实内嵌式ABH可以有效保证宽频减振降噪效果。但也发现单一内嵌式ABH操控与耗散低频振动能量的能力略显不足。早期Aklouche等[9]对内嵌单个ABH板的色散关系的研究表明，单个声学黑洞有效作用频率范围受ABH特征尺寸的限制，对于幂指数m=2的单个ABH，ABH区域的长度越长，ABH效应起始频率越低，也暗示单个ABH在航空装备中的应用局限性。因此突破ABH有效作用频率限制的研究对于ABH在航空领域的应用有着重要意义。Conlon等[10-11]对包含多个ABH板声振特性的数值和试验研究初步表明，ABH阵列诱发的低阶局部模态可以有效弥补ABH设计在中低频性能不足的短板。赵流现[12]通过数值分析方法研究ABH型夹层板的振动特性，结果表明，ABH阵列结合约束阻尼层能显著提高夹芯板的低频损耗因子，降低结构振动响应。由此人们越来越多地关注阵列结构在改善ABH中低频波操控特性方面的可行性。

受局部共振声子晶体和声学超材料结构[13-14]实现低频波的操控这一思想的启发，学者们开始尝试将周期ABH结构与局域共振思想结合起来，ABH的周期性栅格结构可以看作一种声子晶体结构，由内嵌式ABH在梁或者板结构中阵列形成。唐利玲等[15-16]首次在一维（1D）周期ABH梁中发现带隙现象，并通过试验和仿真得到了证实，随后研究者提出在ABH区域附加质量块，拓宽低频带隙[16-17]，并将研究拓展到具有一维周期性的ABH板[18]。研究表明，包含1D ABH的一维阵列设计产生带隙的本质与布拉格（Bragg）散射和局部共振的共同作用相关，且ABH结构表现出不同于传统附加振子的本征型多频局部共振特征，有助于实现多个宽频带隙。季宏丽等[3， 19]对1D ABH和2D ABH中的弯曲波传播特性研究表明，2D ABH往往表现出比1D ABH更为复杂的操控特点，且在常见的板类结构设计中：（1） 2D ABH中的波传播路径更复杂[3]；（2） ABH之外的板的均匀部分容易保留更多能量传输路径，通过ABH元胞的波未能全部由ABH捕捉。板类结构设计通常需要考虑单元在两个维度方向的分布，针对2D ABH二维阵列的弯曲波操控也成为研究难点。2015年，Zhu Hongfei等[20]分析了2D ABH按照正方晶格排布的色散特性，但并未发现显著的全方向带隙。为了在包含ABH的周期板结构中实现全方向带隙，唐利玲等[21]在具有二维周期性的ABH阵列板结构中，设计2D ABH间距小于其直径，保留尽可能少的均匀区域，以保证弯曲波可以完全进入ABH结构，并引入附加质量，增强Bragg散射效果，拓宽带隙。

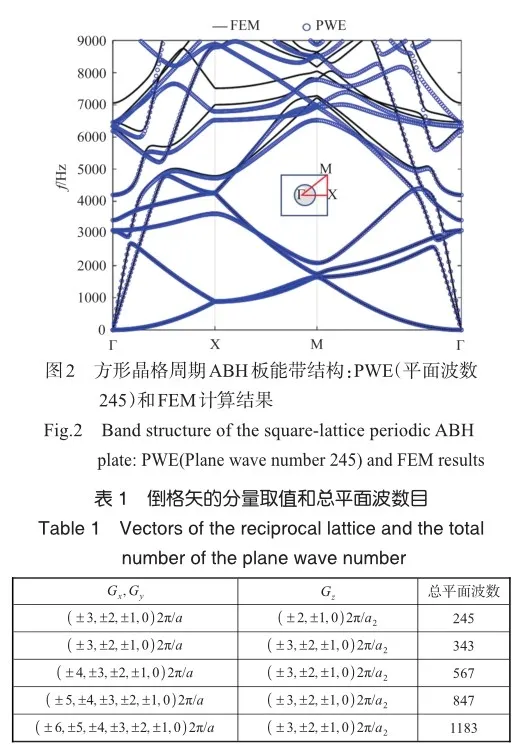
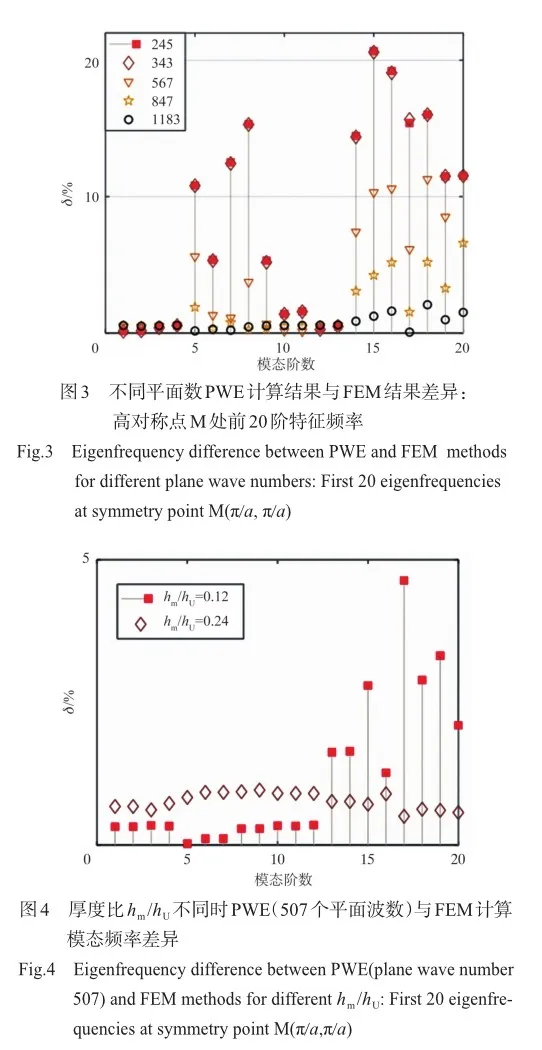
以上针对二维声学黑洞声子板的研究主要考虑最初由Krylov[22]提出的无中心平台的ABH凹坑结构，黄薇等研究发现含中心平台的新型ABH凹坑表现出不同于传统无中心平台ABH的弯曲波传播特征，即弯曲波聚集在偏离ABH凹坑中心的位置。目前针对2D ABH阵列的研究鲜有明晰含中心平台ABH与无中心平台ABH所构造周期结构中弯曲波传播特征的区别。为了丰富周期ABH结构波操控特性的理论研究基础，本文面向航空装备中常用的板类结构，从内嵌周期ABH板出发，研究含中心平台2D ABH板中的弯曲波传播问题。首先通过对比平面波展开（PWE）方法和有限元（FEM）方法分析周期ABH板实能带结构的差异，分析PWE方法的收敛性并明晰该方法在何种情况下适用于分析周期ABH结构的能带结构。其次主要通过FEM方法分析由含中心平台ABH构造的ABH声子板的能带结构，通过分析本征模态、稳态波场和能量分布特征，讨论了含中心平台和无中心平台ABH构造的周期ABH结构操控弯曲波传播的区别。最后探究了ABH截面特征参数对能带结构的影响规律。

1 分析方法

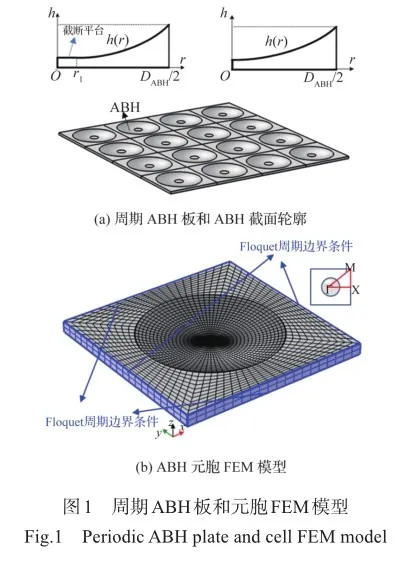
本节针对含中心平台和无中心平台的ABH截面设计，分析了其分别以方形格子阵列所构成周期ABH板的能带结构，探讨含中心平台ABH截面参数对实能带结构的影响规律。考虑图1（a）中所示两种非理想2D ABH截面设计构型，含中心平台[3]和无中心平台[23]

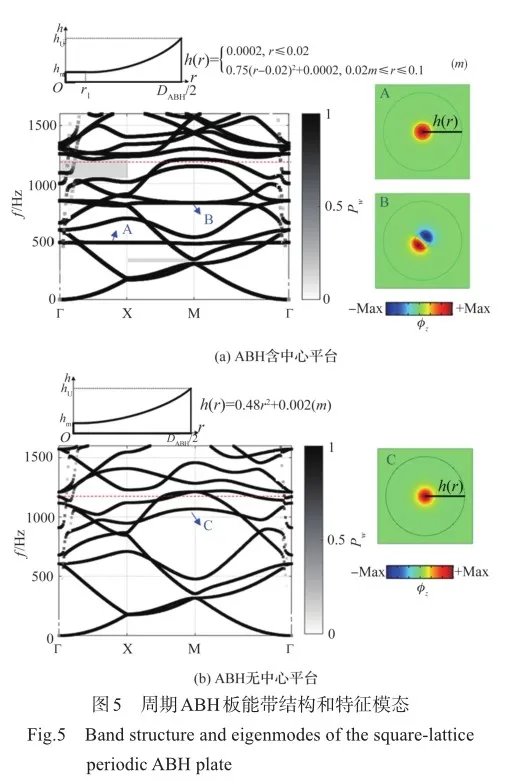
对于ABH直径DABH/2=0.1m，无中心平台的ABH所构成周期结构，其对应的能带结构如图5（b）所示。对比图5（a）可以发现，具有中心平台的周期ABH结构在1.6kHz范围内具有更密集的弯曲波模态。包含无中心平台ABH的方形晶格周期结构并未表现出明显的方向带隙。对比两种ABH截面设计的特征模态，如图5能带结构中A、B、C点标记的特征模态，由振型面外分量？z表示。典型的局部共振声子晶体的研究指出，局部共振模态对应的能带表现为平直带[13]，图5含中心平台的ABH设计对应的能带结构，更容易在低于ABH全波长特征频率fFull=1205Hz时呈现较密集的平带，说明含中心平台的ABH设计更易获得局部振动模态。

以上分析表明，即使中心平台的引入并未打开全方向带隙，但对800Hz以上色散曲线的变化规律也产生了不可忽略的影响。除了带隙特性之外，周期结构会使得弹性波在某些通带频率下仅沿着特定的方向传播，即弹性波方向性传播[25]。为了进一步理解引入中心平台后，周期ABH结构对结构中弹性波传播方向操控的影响规律，建立了如图6（a）所示的ABH板FEM数值分析模型，板中嵌入12×12个ABH，为了消除边界对弹性波传播特性的影响，在模型的四周都设置了完美匹配层（PML）[26]。在ABH阵列的中心处输入垂直于xy平面的单位幅值的简谐力激励，模拟产生弯曲波，分析频域波场特征。为了降低计算时长，引入对称边界条件，对计算模型进行简化，如图6（b）所示。

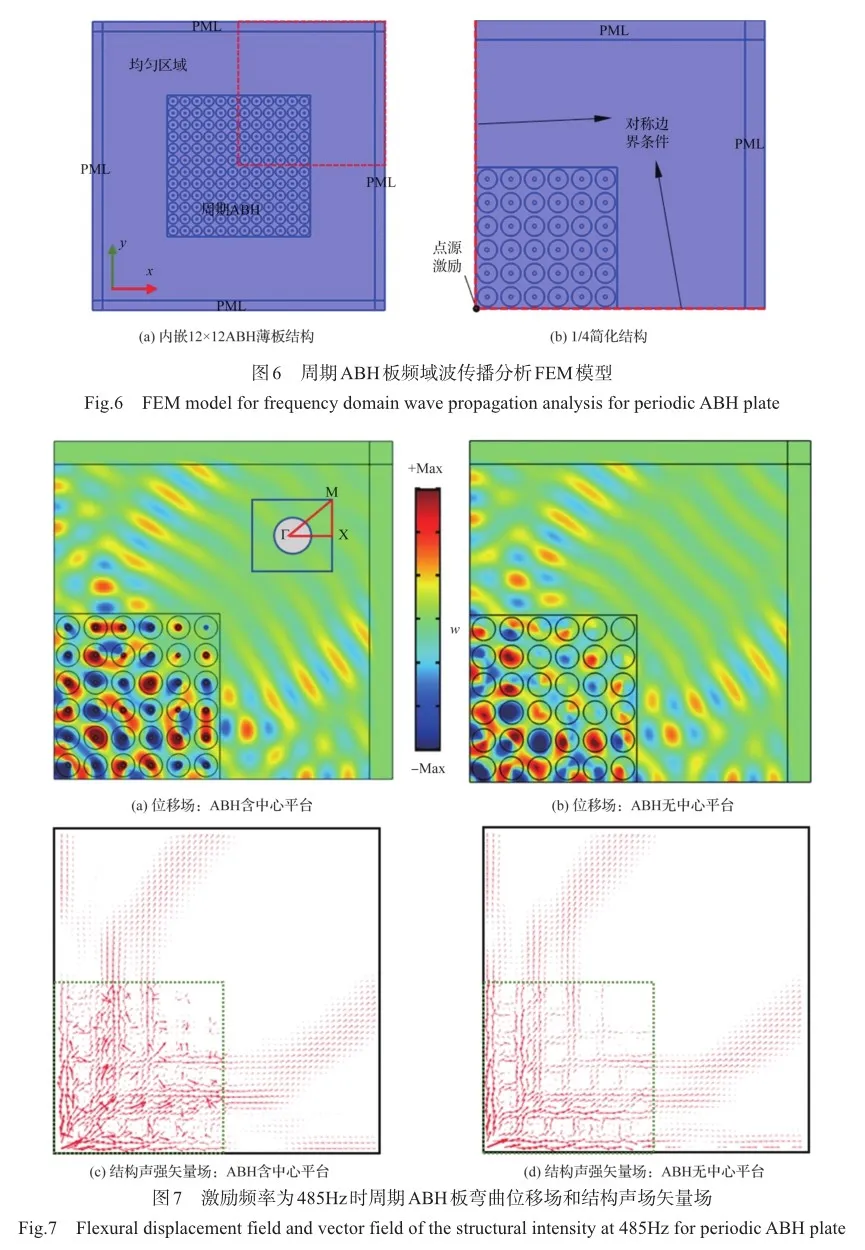
观察激励频率为1165Hz时，图8（a）和图8（b）所示两种周期ABH板结构中的弯曲波场，可以发现，两种结构中的ABH区域均表现出显著的局部共振，但是弯曲波在经过两种不同的ABH栅格后，主要传播方向有所不同。对于含中心平台的周期ABH结构，经过ABH栅格后弯曲波传播主要在MX方向；而对于无中心平台的周期ABH结构，经过ABH栅格后弯曲波沿各个方向传播。图8（c）和图8（d）两个周期ABH板结构的SI矢量场显示，随着传播距离的增大，结构中能量主要向ABH区域汇聚，使得均匀部分振动很弱。以上分析说明在不改变2D ABH直径的情况下，通过引入中心平台的方式改变 ABH截面特征，会在ABH半波长特征频率附近形成较为显著的局部共振特征，从ABH全波长特征频率附近开始，会对ABH栅格的波操控特性造成显著影响。

3 声学黑洞特征参数影响

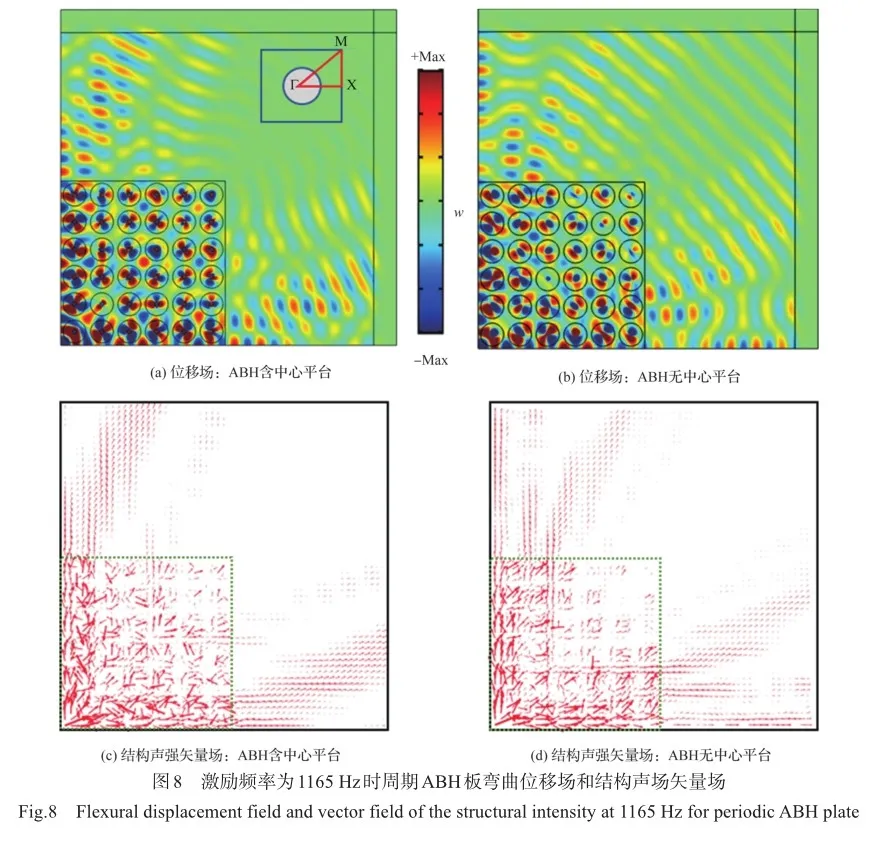
由于ABH单元的局部波动特性会受到其截面设计参数的影响，以ГX方向波传播特性为例，本节分析ABH直径DABH/2=0.1m，含中心平台ABH截面设计参数对能带结构的影响。图9所示为不同中心截断厚度hm对应的能带结构，其他ABH截面设计参数m =2，r1=0.02m。可以看出，中心截断厚度越小，能带结构中平直带越显著，即ABH单元表现出的局部振动越显著，这是由于ABH结构中心厚度越小，ABH能量聚集越显著[3]，且低于ABH全波长特征频率fFull=1205Hz时，局部振动模态更容易形成。中心截断厚度变厚使得难以形成显著的局部共振，从而能带结构变得更加简单，以至于方向带隙也逐渐变窄，同时方向带隙的带边亦发生变化。如hm=0.0006m时，仅有1390～1410Hz和1080～1120Hz两个很窄的方向带隙，而hm=0.0012m时，仅有1245～1295Hz一个很窄的方向带隙。此外，截断厚度较小时，方向带隙的带边对应为非对称点处的模态；而当截断厚度为0.0012m，即其和板厚比值hm/hU=0.24时，带边对应为高对点Г和X处的模态。

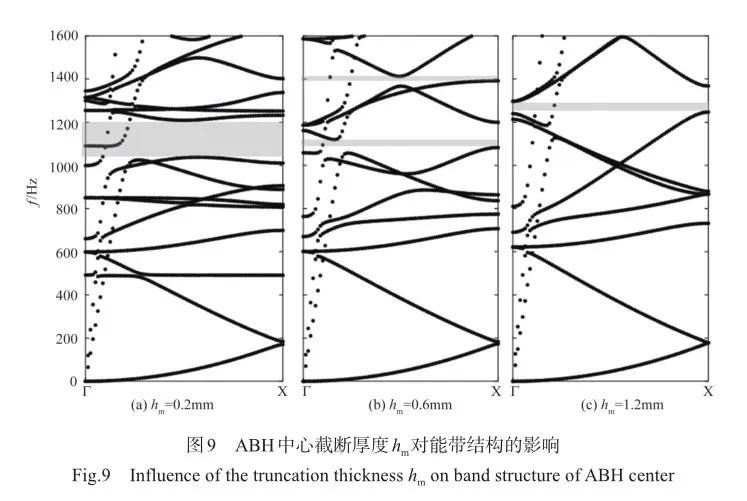
当ABH中心最薄厚度hm=0.0002m、r1=0.02m时，能带结构随ABH幂指数m的变化如图10所示。可以看出，m=1.5时，低于ABH全波长特征频率fFull=1205Hz，存在1050～ 1120Hz和1220～1295Hz两个窄方向带隙。而m>2时，更加平直且密集的能带形成连续且较宽的方向带隙，m=3时方向带隙覆盖频率范围1250～1420Hz。幂指数m的增大使得能带中出现较多的平带，即较多的模态表现出显著的局部振动，且低于fFull=1205Hz时，局部振动模态更容易形成，这是因为ABH截面设计幂指数m≥2时，ABH凹坑可以有效实现ABH效应[28]，实现能量聚集，保证局部共振模态的实现。虽然在不违背ABH理论的平滑性准则[29]情况下，幂指数m的增大可以提升ABH能量聚集效果，增加ABH特征频率附近以及该频率以下的局部共振模态数目，但是过大的幂指数（如m=3）时，许多平直的能带分支直接穿越其他的斜率不为零的能带分支，这并不会促进方向带隙的打开。

当ABH中心最薄厚度hm=0.0002m、幂指数m=2时，能带结构随ABH中心平台半径r1的变化如图11所示。当中心平台半径逐渐变小的时候，能带结构越来越接近于图5（b）中无中心平台ABH的能带，局部振动的平直带逐渐减少，且方向带隙逐渐变窄。r1=0.01m时，低于特征频率1205Hz时，还存在1020～1070Hz和1180～1270Hz两个较窄的方向带隙，当r1减小至0.005m时，则只有1040～1115Hz一个窄方向带隙。r1的增大所导致的能带平带逐渐增多，进一步证实了在ABH设计中，引入中心平台有利于在低于ABH特征频率时，形成局部振动模态。需要注意的是，当中心平台过大时，ABH区域截面厚度变化函数易违背ABH理论的平滑性准则。

4 结论

本文利用有限元方法对2D ABH按照方形晶格排布的周期薄板结构的弯曲波操控特性进行研究，通过研究能带结构和结构声强矢量场特征，分析了含中心平台ABH与传统无中心平台ABH构成的周期板结构中弯曲波传播特性的区别，结合有限元结果明确了平面波展开方法的收敛性和适用条件。FEM方法和PWE方法计算的能带结果对比表明，PWE方法适用于分析ABH中心最薄厚度与均匀区域厚度比hm/hU比较大的情形。

针对含中心平台ABH的周期ABH板和周期ABH条带的能带结构和能量分布特征分析，发现含中心平台ABH易在低于全波长特征频率时获得表征局部共振的平直带，这些模态对应的能带类似于传统局部共振声子晶体中典型的平直带，更容易打开方向带隙。从ABH全波长特征频率附近开始，含中心平台ABH构成的周期板结构较容易实现弯曲波能量的定向传播。通过研究ABH截面特征参数对弯曲波能带结构的影响，发现内嵌式ABH截面的变化对半波长特征频率附近及以下弯曲波的传播特性影响比较小。对于含中心平台的ABH设计，减小中心截断厚度、增大中心平台半径、截面多项式函数幂次大于2时，更容易在低频实现较多表征局部共振的平直带，有助于形成连续且宽频的方向带隙。本文针对ABH阵列的波操控特性研究对后续利用2D ABH实现航空装备板结构中宽频弯曲振动能量的引导有重要理论意义。

参考文献

[1]葛文杰， 张永红， 刘博， 等. 基于超弹性材料拓扑优化方法的变形翼结构设计[J]. 航空科学技术， 2022， 33（12）： 70-80. Ge Wenjie， Zhang Yonghong， Liu Bo， et al. Structural design of deformable wing based on hyperelastic material topology optimization method[J]. Aeronautical Science & Technology， 2022， 33（12）： 70-80. （in Chinese）

[2]邵敏强， 宋杰， 姚鹏， 等. 颗粒阻尼器耗能特性及振动抑制研究[J]. 航空科学技术， 2023， 34（6）： 86-94. Shao Minqiang， Song Jie， Yao Peng， et al. Study on energy dissipation characteristics and vibration suppression of particle damper[J]. Aeronautical Science & Technology， 2023， 34（6）： 86-94. （in Chinese）

[3]Huang Wei， Ji Hongli， Qiu Jinhao， et al. Wave energy focaliza‐ tion in a plate with imperfect two-dimensional acoustic black hole indentation[J]. Journal of Vibration and Acoustics， 2016， 138（6）： 061004.

[4]Tang Liling， Cheng Li， Ji Hongli， et al. Characterization of acoustic black hole effect using a one-dimensional fully-coupled and wavelet-decomposed semi-analytical model[J]. Journal of Sound and Vibration， 2016， 374： 172-184.

[5]O’Boy D J， Krylov V V. Damping of flexural vibrations in circular plates with tapered central holes[J]. Journal of Sound and Vibration， 2011， 330（10）： 2220-2236.

[6]Ji Hongli， Wang Xiaodong， Qiu Jinhao， et al. Noise reduction inside a cavity coupled to a flexible plate with embedded 2D acoustic black holes[J]. Journal of Sound and Vibration， 2019， 455（1）： 324-338.

[7]王小东， 秦一凡， 季宏丽. 基于声学黑洞效应的直升机驾驶舱宽带降噪[J]. 航空学报， 2020， 41（10）： 11. Wang Xiaodong， Qin Yifan， Ji Hongli， et al. Broadband noise reduction inside the helicopter cockpit by acoustic black hole effect[J]. Acta Aeronautica et Astronautica Sinica，2020， 41（10）： 11. （in Chinese）

[8]王小东， 季宏丽， 裘进浩. 声学黑洞原理的双层加筋板-腔系统降噪研究[J]. 振动工程学报， 2022， 35（2）： 503-513. Wang Xiaodong， Ji Hongli， Qiu Jinhao. Noise reduction of a double-layer stiffened plate-cavity system based on acoustic black hole principle [J]. Journal of Vibration Engineering， 2022， 35（2）： 503-513. （in Chinese）

[9]Aklouche O， Pelat A， Maugeais S， et al. Scattering of flexural waves by a pit of quadratic profile inserted in an infinite thin plate[J]. Journal of Sound and Vibration， 2016， 375： 38-52.

[10]Conlon S C， Fahnline J B， Fabio S. Numerical analysis of the vibroacoustic properties of plates with embedded grids of acoustic black holes[J]. Journal of the Acoustical Society of America， 2015， 137（1）： 447-457.

[11]Feurtado P A， Conlon S C. An experimental investigation of acoustic black hole dynamics at low， mid， and high frequencies[J]. Journal of Vibration and Acoustics， 2016， 138（6）：1-10.

[12]Zhao Liuxian. Low-frequency vibration reduction using a sandwich plate with periodically embedded acoustic black holes[J]. Journal of Sound and Vibration， 2019， 441： 165-171.

[13]温熙森， 温激鸿， 郁殿龙， 等. 声子晶体[M]. 北京： 国防工业出版社， 2009. Wen Xisen， Wen Jihong， Yu Dianlong，et al.Phononic crystals[M]. Beijing： National Defense Industry Press， 2009. （in Chinese）

[14]赵瑞， 严昊， 席柯. 声学超表面抑制第一模态研究[J]. 航空科学技术， 2020， 31（11）： 104-112. Zhao Rui，Yan Hao，Xi Ke，et al. Research on acoustic metasur‐faces for the suppression of the first mode[J]. Aeronautical Sci‐ence & Technology， 2020， 31（11）： 104-112.（in Chinese）

[15]Tang Liling，Cheng Li. Broadband locally resonant band gaps in periodic beam structures with embedded acoustic black holes[J]. Journal of Applied Physics， 2017， 121（19）： 194901.

[16]Tang Liling， Cheng Li. Ultrawide band gaps in beams with double-leaf acoustic black hole indentations[J]. Journal of the Acoustical Society of America， 2017， 142（5）： 2802.

[17]Tang Liling，Cheng Li. Impaired sound radiation in plates with periodic tunneled Acoustic Black Holes[J]. Journal of Applied Physics， 2020， 135： 106410.

[18]Tang Liling，Cheng Li. Periodic plates with tunneled AcousticBlack-Holes for directional band gap generation[J]. Mechanical Systems & Signal Processing， 2019， 133： 106257.

[19]Ji Hongli， Luo Jing， Qiu Jinhao， et al. Investigations on flexural wave propagation and attenuation in a modified one-dimensional acoustic black hole using a laser excitation technique[J]. Mechanical Systems & Signal Processing， 2018， 104： 19-35.

[20]Zhu Hongfei， Semperlotti F. Phononic thin plates with embedded acoustic black holes[J]. Physical Review B， 2014， 91（10）： 39-43.

[21]Tang Liling， Cheng Li， Chen Kean. Complete sub-wavelength flexural wave band gaps in plates with periodic acoustic black holes[J]. Journal of Sound and Vibration， 2021， 502： 116102.

[22]Krylov V V. Acoustic “black holes” for flexural waves and their potential applications[C]//Proceedings of the Institute of Acoustics Spring Conference， 2002： 25-27.

[23]Krylov V V. Geometrical-acoustics approach to the description of localized vibrational modes of an elastic solid wedge[J]. Soviet Physics-Technical Physics， 1990， 35（1）： 137-140.

[24]郁殿龙.基于声子晶体理论的梁板类周期结构振动带隙特性研究[D]. 长沙： 国防科学技术大学， 2006. Yu Dianlong， Research on the vibration band gaps of periodic beams and plates based on thetheory of phononic crystals [D]. Changsha： National University of Defense Technology， 2006.（in Chinese）

[25]Wen Jihong， Yu Dianlong， Wang Gang， et al. The directional propagation characteristics of elastic wave in two-dimensional thin plate phononic crystals[J]. Physics Letters A， 2007， 364 （3-4）： 323-328.

[26]Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics， 1994， 114（2）： 185-200.

[27]Gavric L， Carlsson U， Feng L. Measurement of structural intensity using a normal mode approach[J]. Journal of Sound and Vibration， 1997， 206（1）： 87-101.

[28]Mironov M A. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval[J]. Soviet Physics： Acoustics， 1988， 34（3）： 318-319.

[29]Feurtado P A， Conlon S C， Semperlotti F. A normalized wave number variation parameter for acoustic black hole design[J]. Journal of the Acoustical Society of America， 2014， 136（2）： 148-52.

Flexural Wave Mainpulation Characteristics of a Periodic Plate with Embedded 2D Acoustic Black Holes

Han Bing， Ji Hongli， Qiu Jinhao

State Key Laboratory of Mechanics and Control of Aerospace Structures， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China

Abstract： Acoustic Black Hole （ABH） structure can be achieved by tailoring the thickness of a structure according to a power function， thus altering the phase velocity of the flexural wave by changing the impedance and enabling energy focalization. The ABH provides a new idea for vibration and noise control in aerospace structures. The ABH array shows the potential to improve wave manipulation characteristics of the ABH design at the middle-low frequency. This paper focuses on studying the flexural wave propagation in a thin plate with embedded periodic two-dimensional （2D） acoustic black holes. The ABH that differs from the classical one proposed by Krylov is centrally with a platform and expected to obtain different wave manipulation properties when it is arranged in the square lattice. The band structure of an infinite periodic ABH plate and the structural intensity vector field in a finite plate with ABH lattice are scrutinized by establishing finite element models. The comparison of band structure results from finite element and plane wave expansion methods clarifies the convergence and appl_{w3YZgx1BelDE9SNMJvw2+Q==}icable conditions of the plane wave expansion method. Numerical results show that the ABH with a central platform is easy to obtain a flat band representing local resonance at low frequency when it is arranged in the square lattice. Near or above the full-wavelength characteristic frequency of the 2D ABH， the square lattice consisting of the ABH with a central platform shows different wave energy direction propagation from the ABH without a central platform. Finally， the influence of ABH cross-section parameters on the band structure is analyzed. The results show that ABH profile parameters have less effect on band structure below the half-wavelength characteristic frequency. The reduction of the central truncation thickness， the increase of the central platform radius， and the power exponent larger than 2 are conducive to forming a broadband directional band gap.

Key Words： ABH； flexural waves； plane wave expansion method； finite element analysis； local resonance