永磁同步电机电流环的二自由度内模控制

摘 要：目前工业上在对永磁同步电机（permanent magnetic synchronous motor， PMSM）进行控制时，常认为电流环的调节过程远快于转速环的调节过程，进而忽略电流环中反电动势扰动项的变化。但对于采用PI控制且机械时间常数与电磁时间常数相差不大或更小的电机而言，若直接对电流环中的反电动势扰动项进行忽略，将会导致电机的动态响应性能恶化。为解决上述问题，本文首先建立了永磁同步电机调速系统的数学模型，并根据此数学模型推导了PI控制条件下电机动态性能变差的原因，以及反电动势扰动项能否进行忽略的条件，针对无法忽略的情况本文在传统内模控制的基础之上设计了一种二自由度内模控制器，该控制器具有2个可独立调节的参数，可分别调节电流环的跟踪特性与鲁棒特性和抗干扰特性。最后，利用Matlab/Simulink对所设计的二自由度内模控制器与传统的PI控制器进行对比仿真实验。结果表明，相比于PI控制器，所设计的二自由度内模控制器使电流环具有更好的跟踪性和鲁棒性，解决了特殊情况下电机动态响应性能变差的问题。

关键词：永磁同步电机（PMSM）；电流环；动态特性；内模控制；鲁棒性

中图分类号：TM301.2 DOI：10.16375/j.cnki.cn45-1395/t.2024.04.010

0 引言

由于永磁同步电机（permanent magnetic synchronous motor， PMSM）具有功率密度高、调速范围广等优点，使得以其为核心的伺服系统在工业领域中具有广泛的应用[1-3]。为了使控制系统具有更好的动态性能，常使用双闭环矢量控制的方式对永磁同步电机进行控制，其中电流环是系统高动态性能的关键，电流环的动态响应性能直接影响整个系统的动态响应性能[4]。在对永磁同步电机的电流环进行研究时，常假设电流变化时反电动势近似不变，进而将电流环等效为一阶惯性环节[5-6]。但当电机的机械时间常数小于或者等于电磁时间常数时，若仍认为反电动势近似不变来控制电机，将会导致电流环的输出难以跟上输入，使得电机无法满足高响应能力的控制系统。而永磁同步电机的机械时间常数反映的是电机转速从静止状态达到稳定工作状态所需的时间，在一些对电机反应速度要求较高的场合，如：飞行器、无人车、机器人关节转轴等，常会选用机械时间常数较小的电机[7]。

为了解决永磁同步电机机械时间常数小于或者等于电磁时间常数时，PI控制能力不足的问题，文献[8]提出了一种“PII控制器”，即仍将电流环等效为一阶惯性环节，但在传统的PI控制基础上增加了一个积分环节来消除系统的稳态误差。这种方法最终在理论上做到了电流环对给定信号的无误差，但此方法对电机参数的变化十分敏感，当参数调节不合适时，系统响应不仅会变差甚至系统会ZCaKkeu9t/Gc5Niqpjabyzyklc9ykv6PXWRMh9OV/Uw=有被损坏的风险。文献[9-10]采用了一种前馈补偿的方法，即给系统引入了一项与反电动势大小相同、符号相反的信号，进而抵消了反电动势对系统的影响，使系统等效为一阶惯性环节而动态特性良好。但这种方式需要采集电机的磁链和转速作为已知参数，而电机的磁链和转速均属于时变参数。由于采样延时等时滞因素的影响会使得到的参数有一定的误差，所以这种方式最终取得的效果也不理想。文献[11]介绍了一种内模控制方式，其具有原理简单、实用性强等优点，在合适的控制参数下可使得系统具有良好的目标跟踪特性、抗干扰特性和鲁棒性，适合对电机这种干扰性强、参数时变的系统进行控制。但传统的内模控制只有一个可调参数，调节时需要在跟踪特性和抗干扰特性之间进行抉择，顾此失彼，所以其控制效果并不完美[12-13]。

本文参考文献[14]提出的二自由度内模控制方法，将此方法应用于PMSM的电流环控制之中，并在Matlab/Simulink中做了与传统PI控制的性能对比试验。最终结果表明：二自由度内模控制不仅解决了传统内模控制调参难以取舍的问题，并且其控制效果明显优于PI控制，解决了电流环动态性能恶化的问题。

1 PMSM调速系统的数学模型

1.1 PMSM的数学模型

PMSM是一种非线性、多变量的系统，其在自然坐标系下建立的数学模型具有复杂、多变量、强耦合的特点[15]。为了便于控制，采用矢量控制坐标变换的方式对其数学模型进行解耦和降阶。本文给出了永磁同步电机在d-q同步旋转坐标系下的数学模型。

假设三相PMSM为理想电机，做出如下假定[16]：

①忽略铁心饱和；②不计涡流和磁滞损耗；③转子上无阻尼绕组，永磁体不计阻尼作用；④相绕组中感应电动势波形是正弦波。

其在d-q旋转坐标系下对应的电压方程为

[Ud=RId+LddIddt-ωeLqIq，Uq=RIq+LqdIqdt+ωe（LdId+ψf）.] （1）

电磁转矩方程为

[Te=32PnIq[Id（Ld-Lq）+ψf]，] （2）

式中：[Ud、Uq]为[d、q]轴电压；[Id、Iq]为[d、q]轴电流；[Ld、Lq]为[d、q]轴电感；[R]为定子的电阻；t为时间；[ωe]为电机的电角速度；[ψf]为永磁体的磁链；[Te]为电磁转矩；[Pn]为转子的极对数。

由式（1）可知，[d、q]轴的电压方程仍存在相互耦合的感应电动势项。为使后续工作方便，将耦合项当作扰动项进行处理，令：[Ud0=Ud+ωeLqIq，]

[Uq0=Uq-ωe（LdId+ψf）]，式（1）变为如下形式：

[Ud0=RId+LddIddt，Uq0=RIq+LqdIqdt.] （3）

式（1）中的同步旋转坐标系具有如下规定：其d轴始终与转子总磁链矢量[ψf]的方向重合，称之为直轴，这个方向的电流分量主要是产生励磁的作用；在d轴的方向上逆时针旋转90°便是q轴的方向，称之为交轴，此方向的电流分量主要产生转矩的作用。

当PMSM的转子类型为表贴式时，有：[Ld=Lq=L]。由式（2）知，此时d轴电流对转矩的产生并无贡献，为使在相同转矩条件下所需的电流最小，采用[Id=0]的控制策略。在此条件下，式（2）、式（3）变为如下形式：

电压方程为

[Ud0=RId+LdIddt=0，Uq0=RIq+LdIqdt=Uq-ωeψf.] （4）

电磁转矩方程为

[Te=32PnIqψf.] （5）

由运动学公式得其运动方程为

[dωmdtτ=Te0-Bωm，] （6）

式中：[ωm]为电机的机械转速；[τ]为电机的转动惯量；[Te0=Te-Tl]，[Tl]为负载转矩；[B]为电机的摩擦系数。

对式（4）和式（6）进行拉普拉斯变换，得到其对应的复频域方程为

[Gc（s）=Iq（s）Uq0（s）=Id（s）Ud0（s）=1Ls+R，] （7）

[Gs（s）=ωm（s）Te0（s）=1τs+B]， （8）

式中：[Gc]、[Gs]分别为电流环和速度环电机部分的传递函数。

1.2 逆变器的数学模型

永磁同步电机的控制过程中常使用空间矢量PWM（space vector PWM， SVPWM）技术来控制三相逆变器，进而将直流电压转化为所需的交流电压。SVPWM的理论基础是平均值等效原理，即在一个开关周期内通过对基本电压矢量加以组合，使其平均值与给定电压矢量相等[17]。其工作过程为：首先，根据旋转矢量在两相静止坐标系下的分量判断其所处的扇区；然后，根据平均值等效原理计算出所在扇区主副矢量的作用时间，将其在一个开关周期内进行合理的分配并转换为对应的PWM信号，进而控制逆变器的开关。

基于SVPWM算法控制的逆变器可将其等效为一阶惯性环节，

[Ginv（s）=1Tss+1，] （9）

式中：[Ts]为逆变器的开关周期；因为逆变器的输出与输入相等，因此增益取1。

再考虑到开关延时、死区时间和数字控制延时的影响，将这些影响共同等效为一个延迟环节[e-sTd][ ][18]。因为[Td≪Ts]（[Td]为开关延时、死区时间和数字控制延时的时间总和），故可将此延迟环节按照泰勒级数近似展开为一个一阶惯性环节。综上，考虑延迟和死区时间的SVPWM电压源逆变器传递函数为[19]

[Ginv_d（s）=1（Tds+1）（Tss+1）.] （10）

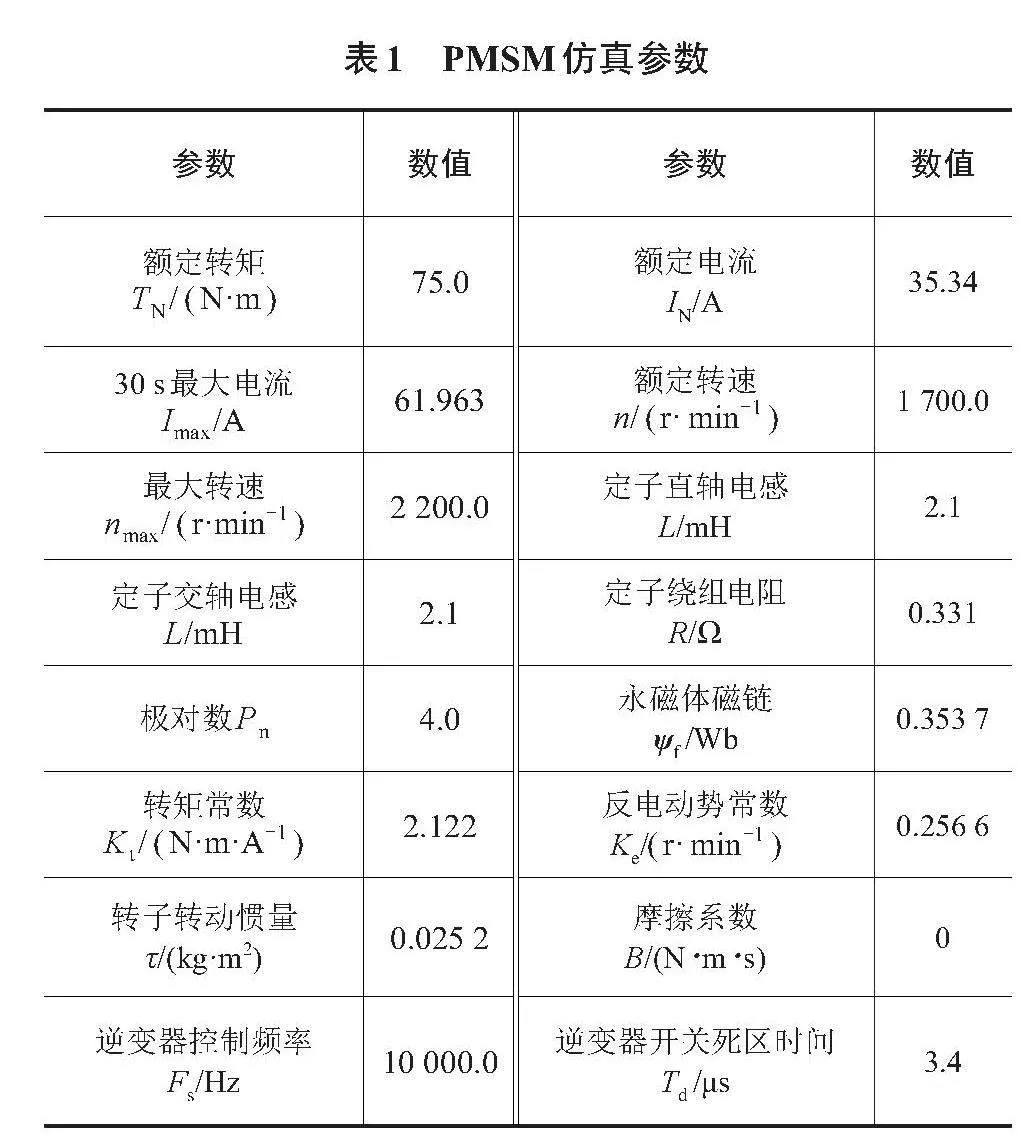
综上，可得永磁同步电机的电流环结构如图1所示。

2 电流环分析

为了方便后续分析问题，假设电机空载运行，电机的摩擦系数忽略不计。令[Kt=32Pnψf，Ke=Pnψf]，此时电流环的结构图如图2所示。

在实际工程中，常认为电机的电流环调节过程远快于转速环的调节过程，从而忽略扰动项[ωe、ψf]的变化，此时电流环的结构图如图3所示。

不做忽略扰动项，由图2可知输出电流与输入电压之间的关系为

[Iq=P/KxYDJs05bM0Iju/WKmmBX6wUXF14+T/ZIZXx8jA8A=s/RTns2+s+1/TmUq，] （11）

式中：[Tn=LR]为电机的电磁时间常数；[Tm=RτKeKt]为电机的机械时间常数。此时电流环的结构框图如图4所示。

将图4中的ACR用PI控制策略进行设计，其表达式为

[GPI（s）=（KP+KIs），] （12）

式中：[KP]为调节器的比例系数；[KI]为积分系数。

利用图3、图4计算输出电流[Iq]与输入电流[I*q]之间的关系。

对于图3，忽略扰动项的情况有：

[Iq3=（KP+KIs）（1（Tds+1）（Tss+1））（1Ls+R）1+（KP+KIs）（1（Tds+1）（Tss+1））（1Ls+R）I*q.] （13）

当输入电流[I*q]为单位阶跃信号时，由终值定理可求得输出[Iq3]为

[Iq3=1.] （14）

可知此时输入等于输出，为理想情况，不存在稳态误差。

对于图4，不忽略扰动项的情况有：[Iq4=（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）1+（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）I*q.] （15）

同理，当输入电流[I*q]为单位阶跃信号时，由终值定理可求得输出[Iq4]为

[Iq4=limt→∞（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）1+（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）I*q=lims→0（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）1+（KP+KI/s）（1（Tds+1）（Tss+1））（s/RTns2+s+1/Tm）·s·1s=lims→0（KI/s）·1·（s/R）·Tm1+（KI/s）·1·（s/R）·Tm=KITmR+KITm.] （16）

可知此时输入与输出并不一定相等，存在稳态误差[EIq4]，

[EIq4=RR+KITm.] （17）

由式（14）和式（16）可得，并不是在任何情况下都可以忽略扰动项。对图4中前向通道的第三项进行分析：

[s/RTns2+s+1/Tm=1/RTns+1+1/（Tms）→s=jωc][ 1/RTnjωc-j/（Tmωc）+1，] （18）

式中，j=[-1]。当[Tnωc≫1Tmωc]时，可忽略[1Tmωc]项，其中[ωc]为系统的截止频率，即

[Tnωc>10Tmωc⇒ωc>31TnTm.] （19）

当式（19）满足时，式（18）有如下形式：

[s/RTns2+s+1/Tm=1/RTns+1=1Ls+R.] （20）

此时图3与图4的传递函数完全相同。因此，式（19）便是能否忽略扰动项的条件。

对于一般的传递系统，机械时间常数远大于电磁时间常数，式（19）的条件一定满足，此时可以对扰动项进行忽略。对于小转动惯量的系统，因其机械时间常数与电磁时间常数相当甚至小于电磁时间常数，此时扰动项势必会对电流环造成影响，应采取措施消除影响。

3 电流环内模控制器设计

内模控制是为受控对象并联一个理想的数学模型，将实际输出与理想输出的差值反馈至控制器的输入端，从而起到抑制模型失配、参数摄动以及外界干扰的作用，进而提高系统的鲁棒性[20]。

3.1 内模控制原理

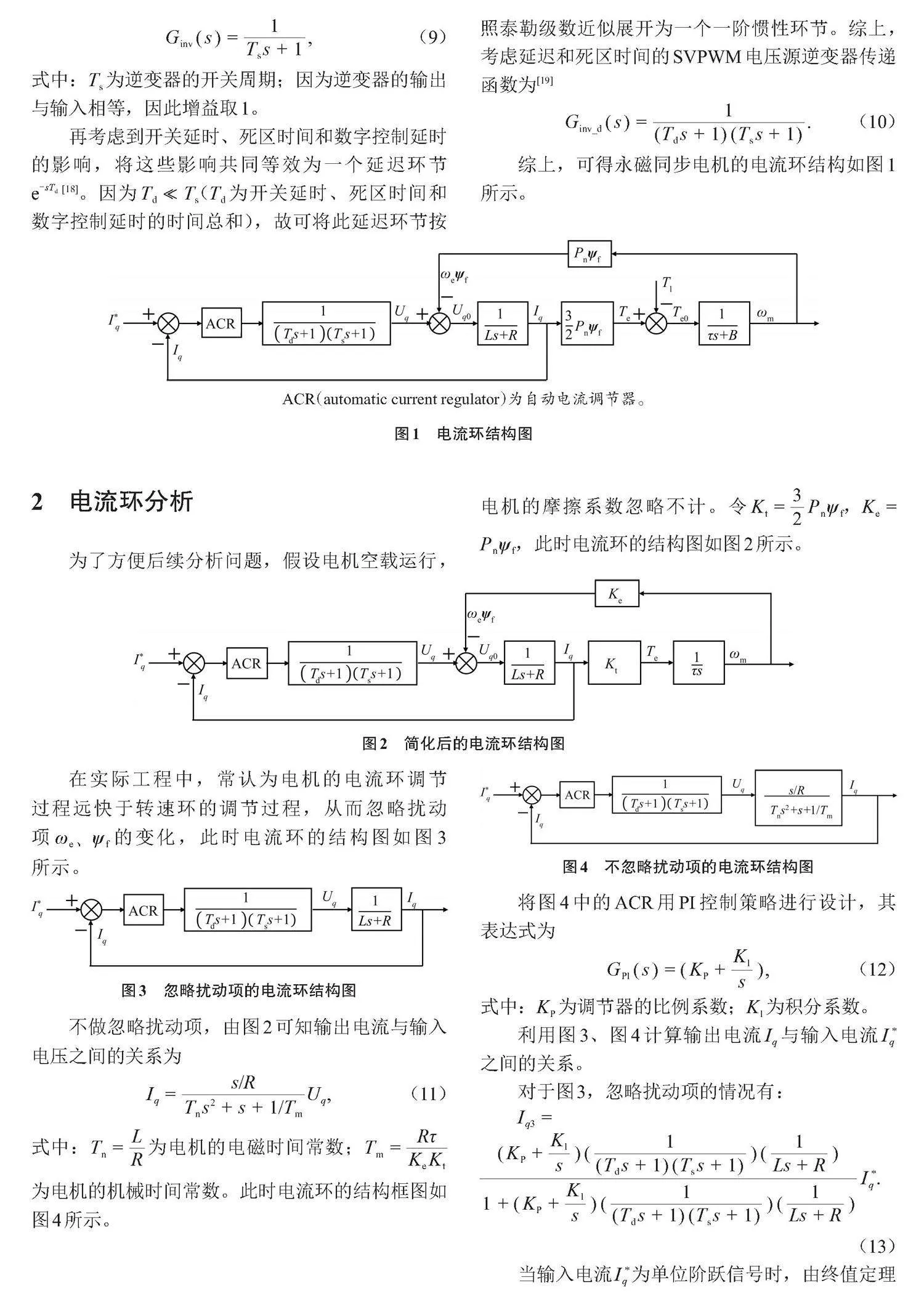
传统的内模控制系统结构图如图5所示。

其中[r（s）、d（s）]和[y（s）]分别为系统的输入、干扰和输出信号；[u（s）]为内模控制器的输出；[Q（s）]为内模控制器；[P（s）]为实际被控对象；[M（s）]为被控对象的理想数学模型。当图5中受控对象的模型建立精确，即[P（s）=M（s）]时，[Q（s）]调节的是[d（s）]引起的误差。当[P（s）]的参数发生摄动，[Q（s）]会对由干扰和参数变化引起的误差进行共同调节。所以内模控制可以抑制因系统的模型失配、参数摄动而带来的影响，能够提高系统的鲁棒性。

对图5的结构进行简化，得到图6。

图6中[C（s）]为

[C（s）=Q（s）1-Q（s）M（s）.] （21）

此时输出[y（s）]与输入[r（s）]之间的关系为

[y（s）=C（s）P（s）1+C（s）P（s）r（s）.] （22）

输出[y（s）]与扰动[d（s）]之间的关系为

[y（s）=11+C（s）P（s）d（s）.] （23）

联立式（21）、式（22）和式（23），可得

[y（s）=Q（s）P（s）1+Q（s）[P（s）-M（s）]r（s）+]

[1-Q（s）M（s）1+Q（s）[P（s）-M（s）]d（s）.] （24）

由式（24）可知，如果被控对象的实际数学模型和理想数学模型完全相同，即[P（s）=M（s）]，则式（24）具有如下形式：

[y（s）=Q（s）P（s）r（s）+[1-Q（s）M（s）]d（s）.] （25）

此时取[Q（s）=M（s）-1]，则

[y（s）=r（s）.] （26）

式（26）便是内模控制理想情况下的控制效果，此时输出[y（s）]始终等于输入[r（s）]。但实际情况下建立的数学模型并不能完全描述受控对象，为使式（26）可实现，通常会在内模控制器中加入低通滤波器[F（s）][ ][21]。

此时内模控制器具有如下形式：

[Q（s）=M（s）-1F（s）.] （27）

其中低通滤波器[F（s）]具有如下形式：

[F（s）=1（βs+1）m，] （28）

式中：[β]用于调节控制器的抗干扰性能；[m]为正整数，用于补偿抗干扰控制器[Q（s）]的相对阶，从而使系统可实现[22]。

联立式（25）、式（27）和式（28）可得

[y（s）=1（βs+1）mr（s）+[1-1（βs+1）m]d（s）.] （29）

由式（29）可知参数[β]与系统的目标值跟踪特性和干扰抑制特性、鲁棒性均有关系。整定参数时需要在这些重要的特性之间进行取舍，易顾此失彼，这正是传统内模控制只有一个自由度的不足之处。

3.2 二自由度内模控制器设计

图7为二自由度内模控制器的简化结构图。

图7由图6推演而来。结合图6，根据图7可得

[y（s）=Q1（s）Q2（s）P（s）1+Q2（s）[P（s）-M（s）]r（s）+]

[1-Q2（s）M（s）1+Q2（s）[P（s）-M（s）]d（s）.] （30）

当控制器中加入低通滤波器，认为[P（s）=M（s）]，此时有

[y（s）=Q1（s）Q2（s）P（s）r（s）+[1-Q2（s）M（s）]d（s）].

（31）

仍然将[Q2（s）]用上述方式进行设计：

[Q2（s）=M（s）-1F2（s），F2（s）=1（βs+1）m.] （32）

联立式（31）和式（32），有

[y（s）=Q1（s）F2（s）r（s）+[1-F2（s）]d（s）.] （33）

对[Q1（s）]进行如下设计，

[Q1（s）=F2（s）-1F1（s），F1（s）=1（αs+1）n，] （34）

式中：[α]为控制器的可调节参数；[n]为正整数，用于补偿控制器[Q1（s）]的相对阶，从而使系统可实现。

将式（34）代入式（33），可得

[y（s）=1（αs+1）nr（s）+[1-1（βs+1）m]d（s）.] （35）

由式（35）可知，二自由度内模控制器具有2个自由度，参数[α]、[β]分别可以对系统的目标值跟踪特性和抗干扰特性与鲁棒性进行独立调节，解决了传统内模控制需要在多个性能之间进行取舍的困扰。

根据第2章的内容可知，

[M（s）=1（Tds+1）（Tss+1）s/RTes2+s+1/Tm，Q2（s）=M（s）-1F2（s）， Q1（s）=F2（s）-1F1（s）.] （36）

其中[F1（s）、F2（s）]以式（32）和式（34）进行设计，为使系统可实现，两者的阶数m和n均取3。

4 仿真分析

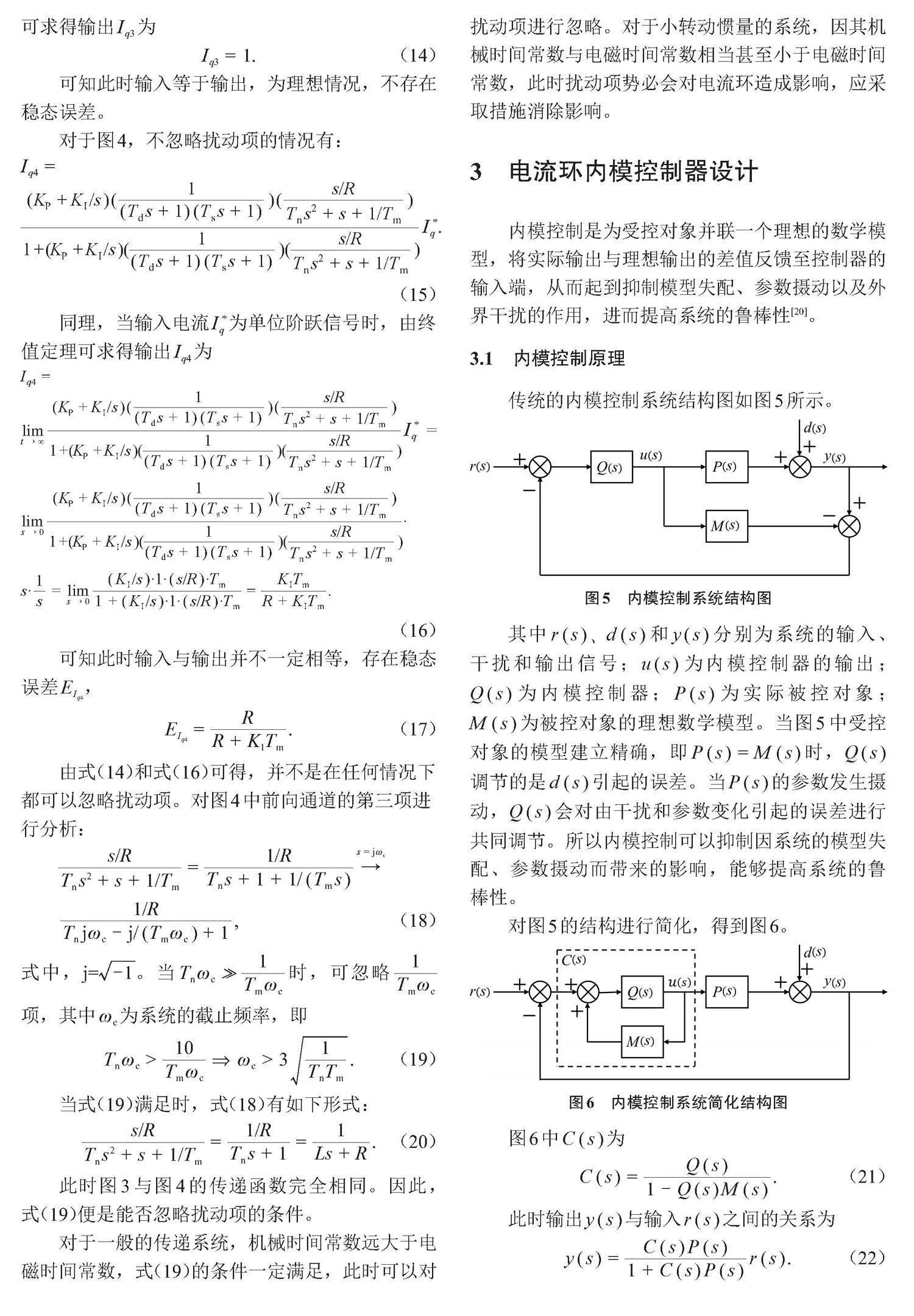
实验所采用的PMSM参数如表1所示。

由表1中的数据和上文中的公式可以计算出该电机的电磁时间常数和机械时间常数分别为：[Tn=6.34 ms]，[Tm=2.78 ms]。由于机械时间常数小于电磁时间常数，所以此时的电机系统如果不对电流环的扰动项做处理，电流将会出现不可忽略的误差。

根据表1中的数据在Matlab/Simulink中构建PMSM系统的双闭环调速模型，采用转子磁链定向的矢量控制并令[Id=0]。在此基础上做了PI控制器（其中KcP= 1 460.36，KcI= 9.26，KsP= 3.06，KsI= 77.08，依据文献（17）中的整定方法得出）与根据式（36）构建的二自由度内模控制器的对比试验，其结果如下。

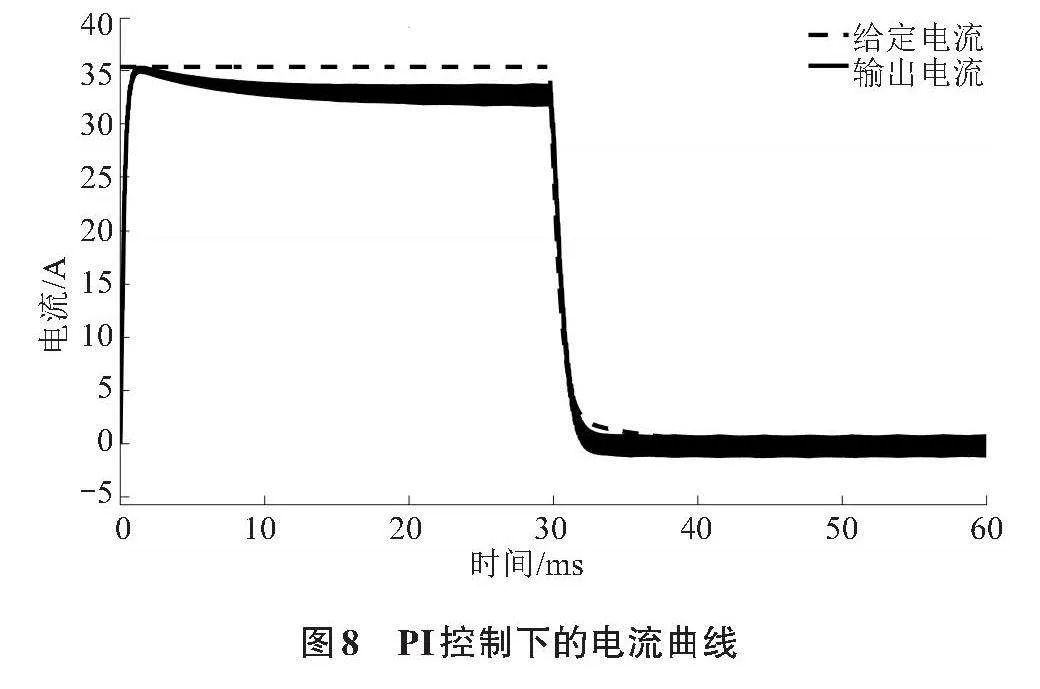
图8为给定800 r/min的转速时，采用PI控制得到的电流曲线。

由图8可以看出在电机加速阶段，输出电流始终小于给定的输入电流，两者之间存在稳态误差，这与式（17）所分析的结果一致，这种电流误差的存在使得电机在加速阶段始终不能以最大电流工作，进而使其在加速阶段花费更长的时间。

图9为相同条件下，根据式（36）构建的内模控制器得到的电流曲线，其中参数[α=0.005Te]，[β=0.003Te]。

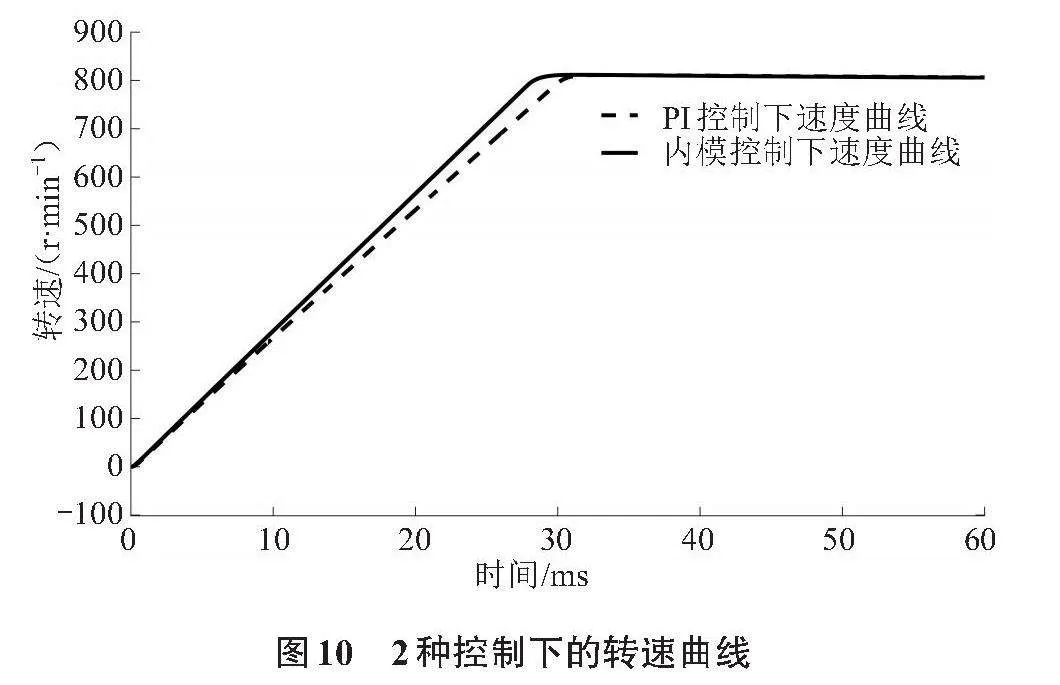
由图9可以看出，在加速阶段其输出电流时刻依附于系统的给定电流，解决了PI控制中的问题。对比图9和图8可以看出，内模控制下的电流开始下降的时间约在27.61 ms，而PI控制约在29.68 ms，这说明内模控制下电机提前到达了给定转速，其提速效果优于PI控制，具体情况如图10所示。

因为内模控制解决了输出电流与给定电流之间的误差问题，其加速阶段能够以理想电流进行，所以在图10中的加速段体现出了内模控制时刻大于PI控制的情况，且内模控制率先加速到给定转速。

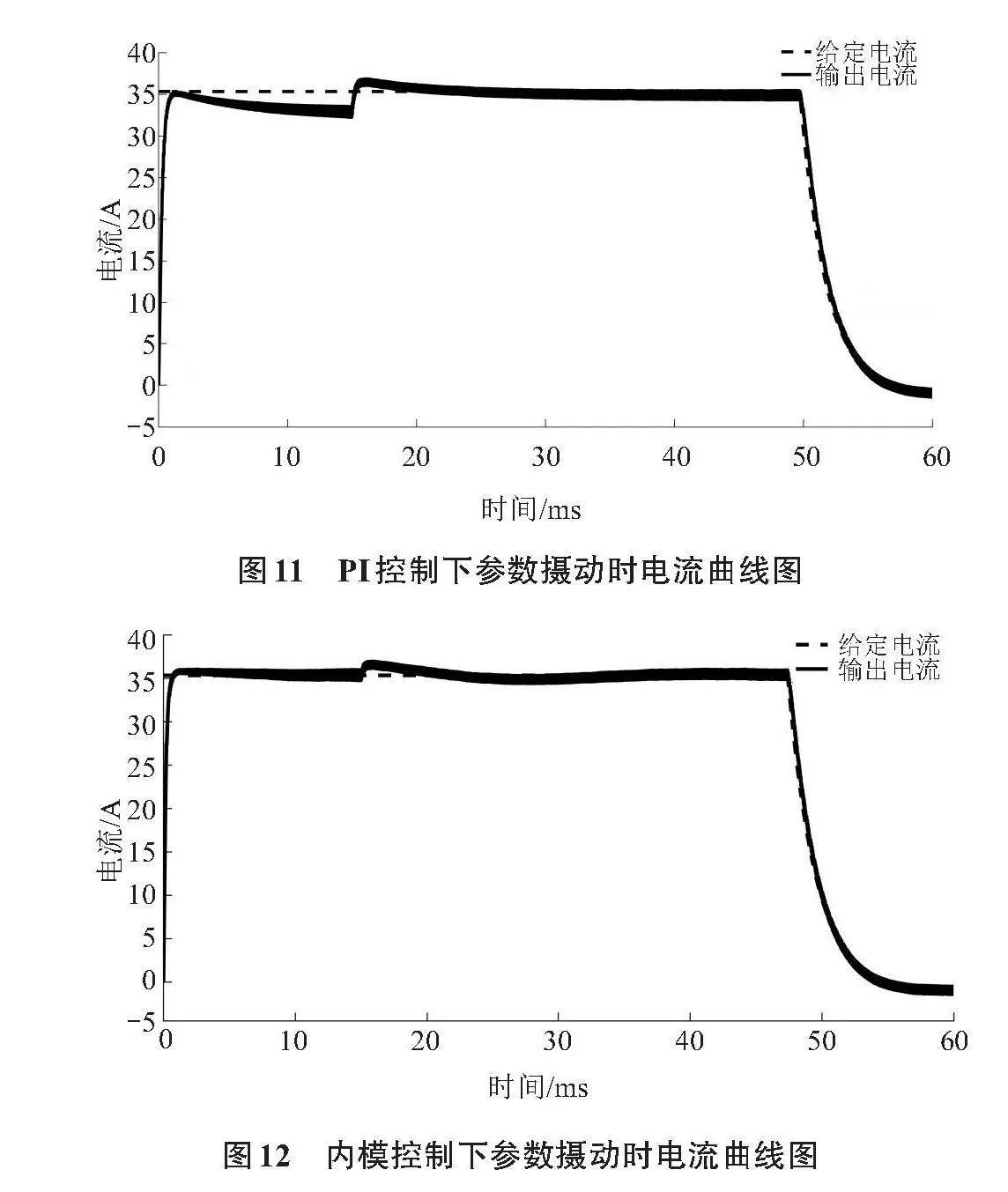
由于电机在运行的过程中有些参数会随着工作环境的变化而发生摄动，为了测试所设计控制器和PI控制器的鲁棒性，在与上文相同的实验条件下，当电机运行至15 ms时将其转子磁链衰减为原来的40%，得到结果见图11、图12。

将图11与图8对比、图12与图9对比，可知内模控制下的系统在参数发生摄动时，其电流波动和调节时间均小于PI控制，因此其鲁棒性更优。

5 结论

本文建立了PMSM调速系统的数学模型，并对电流环使用PI控制的情况进行了分析。由式（14）和式（17）可知，当PMSM的机械时间常数小于或者接近于电磁时间常数时，如对反电动势项忽略，则会使得电机的电流输入与输出之间存在一个明显的稳态误差，这将使得电机的动态性能变差。为解决此问题，本文设计了一种二自由度的内模控制器，由式（35）知其具有2个可独立调节的参数，能分别调节系统的跟踪特性和抗干扰特性，在理论上解决了PI控制的稳态误差问题。最后在Matlab/Simulink上进行了所设计控制器与PI控制器的对比仿真实验，由结果可知，所设计的控制器相比于PI控制器，其电流跟踪特性更好，使得电机具有了更好的加速性能，同时其鲁棒性也明显优于PI控制，有助于小转动惯量永磁同步电机在高性能场合下的应用。

参考文献

[1] 陈卓易，屈稳太.基于PID型代价函数的永磁同步电机模型预测电流_{uWvR57UlGeKqrY4eoSRUSy5lWbr0ZtgwZKwvAEkvER0=}控制[J].电工技术学报，2021，36（14）：2971-2978.

[2] 王丽，高远，袁海英.基于改进型SMO的PMSM无传感器鲁棒控制方法[J].广西科技大学学报，2022，33（2）：48-53.

[3] MA X J，BI C.A technology for online parameter identification of permanent magnet synchronous motor[J].CES Transactions on Electrical Machines and Systems，2020，4（3）：237-242.

[4] 姚绪梁，黄乘齐，王景芳，等.两相静止坐标系下的永磁同步电动机模型预测功率控制[J].电工技术学报，2021，36（1）：60-67.

[5] 陈荣，邓智泉，严仰光.永磁同步伺服系统电流环的设计[J].南京航空航天大学学报，2004，36（2）：220-225.

[6] 万山明，吴芳，黄声华.永磁同步电机的数字化电流控制环分析[J].华中科技大学学报（自然科学版），2007，35（5）：48-51.

[7] 洪帅，高远，张银，等.基于SRUKF的永磁同步电机无传感器控制研究[J].广西科技大学学报，2019，30（1）：46-51.

[8] 杨明，牛里，王宏佳，等.微小转动惯量永磁同步电机电流环动态特性的研究[J].电机与控制学报，2009，13（6）：844-849.

[9] 徐建英，刘贺平.永磁同步电动机参考模型逆线性二次型最优电流控制调速系统[J].中国电机工程学报，2007，27（15）：21-27.

[10] MORIMOTO S，SANADA M，TAKEDA Y.Wide-speed operation of interior permanent-magnet synchronous motors with high-performance current regulator[J].IEEE Transactions on Industry Applications，1994，30（4）：920-926.

[11] 赵曜.内模控制发展综述[J].信息与控制，2000，29（6）：526-531.

[12] LIU J，HUANG M Z，WANG Y.Research on vector-control system of PMSM based on internal model control of current loop[C]//2nd International Workshop on Computer Science and Engineering，Octorber 28-30，2009，Qingdao，China. IEEE，2009：297-301.

[13] HARNEFORS L，NEE H P.Model-based current control of AC machines using the internal model control method[J].IEEE Transactions on Industry Applications，1998，34（1）：133-141.

[14] 张井岗，李临生.一种二自由度内模控制方法[J].工业仪表与自动化装置，2002（4）：63-65.

[15] 解小刚，陈进.采用id=0的永磁同步电机矢量控制系统MATLAB/Simulink仿真[J].新型工业化，2016，6（5）：47-54.

[16] 袁雷，胡冰新，魏克银，等.现代永磁同步电机控制原理及MATLAB仿真[M].北京：北京航空航天大学出版社，2016.

[17] 王光，王旭东，马骏杰，等.一种快速SVPWM算法及其过调制策略研究[J].电力系统保护与控制，2019，47（3）：136-145.

[18] 贺明智，许建平，游小杰，等.环路延时对数字峰值电压控制开关变换器瞬态性能的影响[J].中国电机工程学报，2009，29（6）：1-7.

[19] 王莉娜，朱鸿悦，杨宗军.永磁同步电动机调速系统PI控制器参数整定方法[J].电工技术学报，2014，29（5）：104-117.

[20] 赵志诚，文新宇.内模控制及其应用[M].北京：电子工业出版社，2012.

[21] VANDEURSEN J M，PEPERSTRAETE J A.Internal model control with improved disturbance rejection[J].International Journal of Control，1995，62（4）：983-999.

[22] 杜文龙，陈俐，刘文通，等.考虑延迟的线控转向二自由度内模控制[J].中国机械工程，2021，32（16）：1904-1911.

Two degrees of freedom internal model control of current loop of

permanent magnet synchronous motor

HUANG Bo， PAN Shenghui*， LIU Xingyu

（School of Automation， Guangxi University of Science and Technology， Liuzhou 545616， China）

Abstract： At present， when controlling permanent magnet synchronous motors（PMSM）in industry， it is often believed that the adjustment process of the current loop is much faster than the adjustment process of the speed loop， thereby the changes in the back electromotive force disturbance term in the current loop are neglected. However， for motors that use PI control and have a mechanicaLL9dleppRv20NSjhUbSjUObzhoKr+4uGduxM9jaG+EQ=l time constant that is not significantly different from the electromagnetic time constant or smaller， if the back electromotive force disturbance term in the current loop is directly ignored， it will lead to a significant deterioration in the dynamic response performance of the motor. To solve the above problems， this paper first established a mathematical model of the permanent magnet synchronous motor speed control system. Then， based on this mathematical model， the reasons for the dynamic performance deterioration of the motor under PI control conditions and the conditions that whether the back electromotive force disturbance term can be ignored were derived. In response to the situation that cannot be ignored， this paper designed a two degree of freedom internal model controller on the basis of traditional internal model control. This controller had two independently adjustable parameters that respectively adjusted the tracking characteristics， robustness characteristics， and anti-interference characteristics of the current loop. Finally， a comparative simulation experiment was conducted using Matlab/Simulink to compare the designed two degree of freedom internal model controller with traditional PI controller. The results show that the designed two degree of freedom internal model controller enables the current loop to have better tracking and robustness compared to the PI controller， solving the problem of poor dynamic response performance of the motor under special circumstances.

Keywords： permanent magnet synchronous motor（PMSM）; current loop; dynamic characteristics; internal model control; robustness

（责任编辑：黎 娅）

收稿日期：2023-09-11；修回日期：2023-11-27

基金项目：广西自然科学基金项目（2018GXNSFAA138122）资助

第一作者：黄博，在读硕士研究生

*通信作者：潘盛辉，副教授，研究生导师，研究方向：汽车电子控制技术、自动测试技术等，E-mail：gxustpsh@163.com