丘陵山地小型履带式动力底盘设计与试验

摘 要：针对广西丘陵山地经济作物种植区非结构化的地形以及多种作物种类多的复杂生长环境，设计了一款具有高灵活性、可以适应丘陵山地地形的小型履带式动力底盘。以履带式底盘作为研究对象，建立履带式底盘机器人坡面行走模型，研究其在爬坡时的稳定性与通过性，并在此基础上提出履带式底盘设计方案与参数选取。基于ANSYS Workbench对机架进行受力分析，机架最大位移变形量为0.094 8 mm，最大等效应力为35.611 MPa，满足强度使用要求。利用RecurDyn动力学仿真软件对履带式底盘进行虚拟建模，分析其在爬坡、转向过程中的质心与扭矩变化情况，验证了方案的可行性。田间试验结果表明，履带式底盘机器人在水泥平地直线行驶速度为6.11 km/h，最小转弯半径为403.0 mm，草地最大爬坡角度为38°，最大越障高度为170 mm，作业期间，履带式底盘运行平稳。本文设计的履带式底盘的各项参数能够满足整机设计的要求，具有良好的爬坡越障性能，作业指标达到了相关标准要求，研究成果可为丘陵山地履带式底盘的设计与研发提供参考。

关键词：丘陵山地；履带式底盘；农业机械；RecurDyn

中图分类号：S220.32；TH122 DOI：10.16375/j.cnki.cn45-1395/t.2024.04.003

0 引言

从地形特征角度看，山地和丘陵是广西的主要地形，也是广西重要的经济作物种植区[1-2]。近年来，国家大力发展农业机械，重点开发适用于丘陵山地适度规模化种养殖的轻简型、智能化、复式农机农具。目前，丘陵山地农机动力底盘按照移动方式可分为履带式、轮式、足式和复合式[3]，其中，履带式具有结构紧凑、承载能力强等特点，更适用于丘陵山区农用机械。刘平义等[4]设计了一种采用Y型可调悬架作为调平机构的农用车辆预检测主动调平底盘。曾俊豪等[5]设计了一款除草底盘结构，对底盘的转向性能、稳定性能和越障性能进行了分析。刘九庆等[6]结合转向阻力矩、土壤下陷阻力和履带接地面压力分布情况等参数建立了履带式底盘转向性能模型。Chajkin等[7]建立铰接履带车辆底盘横向稳定性计算的数学模型，对铰接履带车辆横向稳定性进行了研究。Dudzinski等[8]针对履带式底盘能效优化，建立了履带底架内部阻力模型。可见，国内外对履带式底盘也有了不少的研究，但广西丘陵山地地形复杂多样，假如直接使用国内外现有的成熟产品，还存在很多制约因素。

针对广西丘陵山地经济作物种植园区非结构化的地形特点，本文采用模块化的设计方法，设计一种小型履带式动力底盘，并基于虚拟样机技术，借助ANSYS Workbench软件对机架进行分析，利用RecurDyn软件对履带式底盘爬坡与转向进行仿真，完成样机试制，验证设计方案的可行性，为丘陵山地等局部方位内作业空间小的机械化问题与装备提供参考。

1 整体方案设计

1.1 整机系统布置

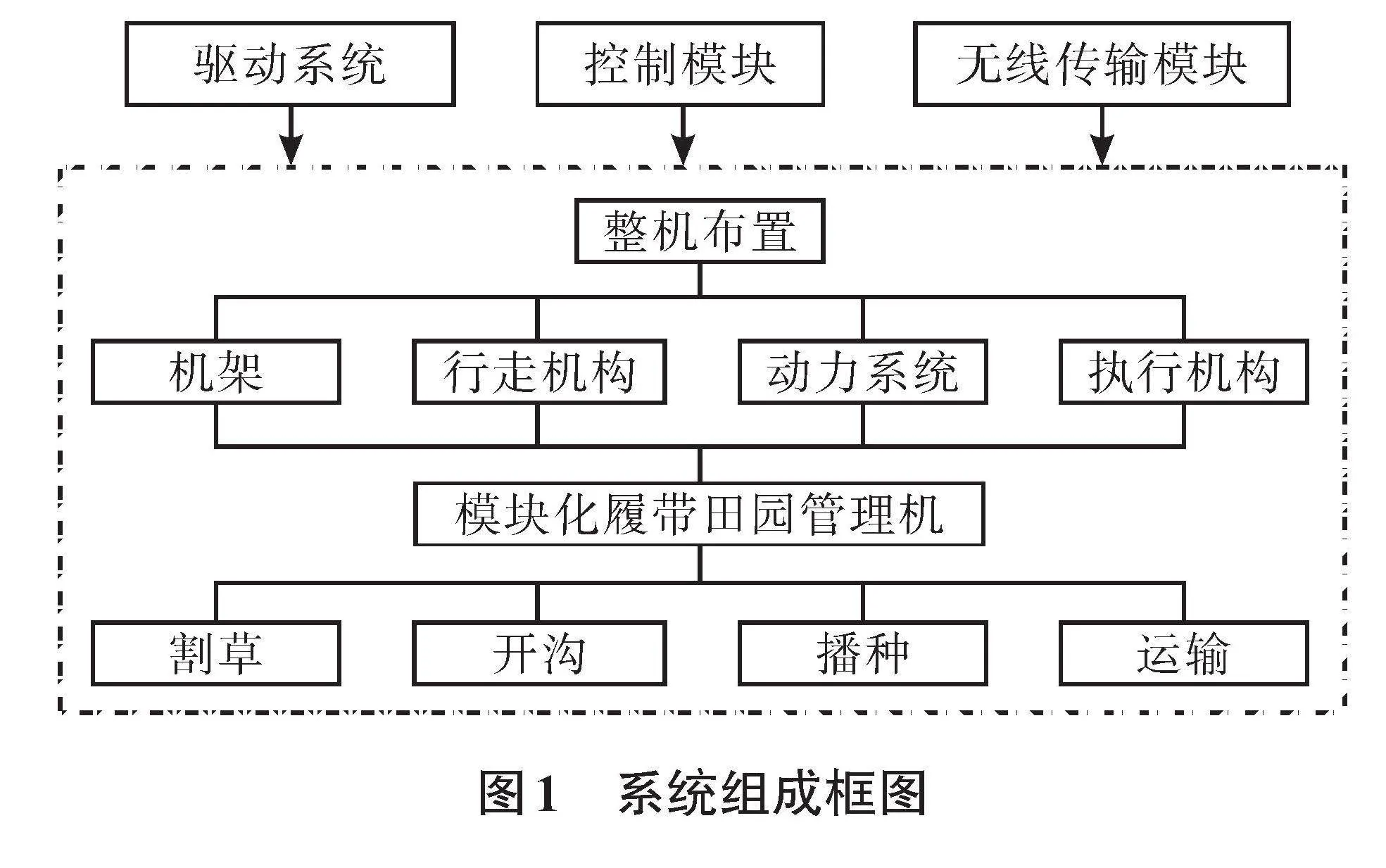
小型模块化履带式动力底盘主要由机架、行走系统、无线传输模块、控制模块以及相关配件组成。机架上安装模块化田园管理机具，如切割装置、施肥装置、货箱等，能够实现割草、开沟、播种、运输等功能。系统组成如图1所示。

小型履带式动力底盘结构组成三维图如图2所示，动力系统采用双电机驱动，通过调节两侧履带驱动电机的转速大小，实现机器不同运动状态的调整[9-10]；履带机构构型采用“一字型”布置，主要部件包括承重轮、驱动链轮、张紧轮与张紧装置等。整机前中部放置模块化田园管理机具，后部放置动力电池与电池管理系统。

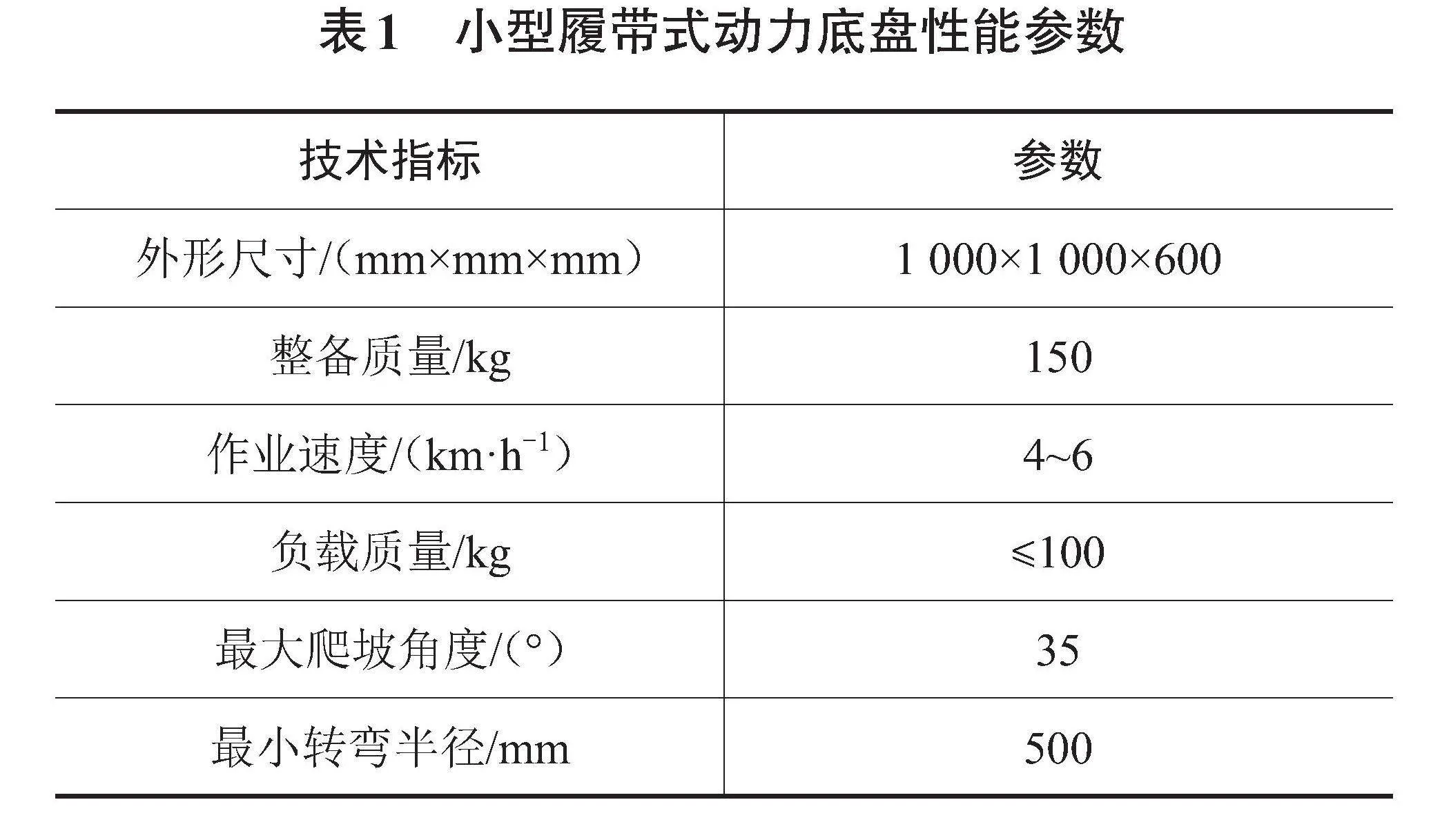
小型模块化履带式底盘总体技术参数如表1所示。

1.2 底盘通过性分析

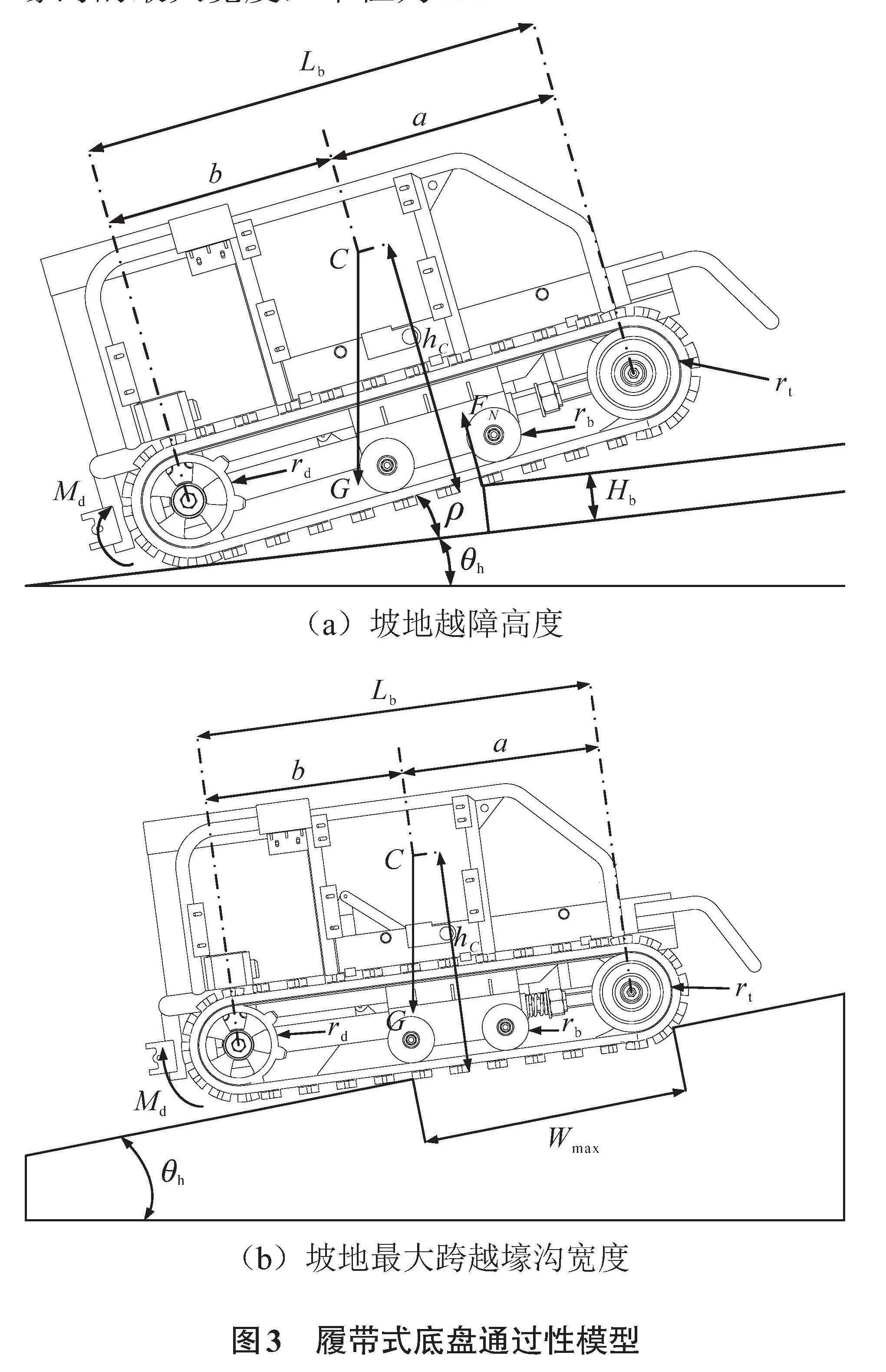
丘陵山地种植田园地形起伏较大，作业环境复杂，对履带式底盘的坡地通过性能提出了较高要求。其中，坡地越障高度与最大跨越壕沟宽度是评价履带式底盘通过性的重要指标[11]。为研究履带式底盘所能翻越障碍物的最c9889a1154d8d47b45a34c623d3defd8大高度与跨越壕沟的最大宽度，建立履带式底盘理想状态下的越障与跨越壕沟模型，如图3所示，其中，Lb为履带接地长度，单位为m；a、b分别为质心位置与前后承重轮的距离，单位为m；C为质心位置；hC为重心到地面的垂直高度，单位为m；Md为驱动链轮扭矩，单位为N·m；rd为驱动链轮半径，单位为m；FN为台阶顶角对履带的支撑力，单位为N；rb为承重轮半径，单位为m；rt为张紧轮半径，单位为m；G为竖直向下的重力，单位为N；ρ为履带式底盘受台阶顶起时的仰角，单位为（°）；Hb为跨越台阶垂直高度，单位为m；θh为坡面角度，单位为（°）；Wmax为跨越壕沟的最大宽度，单位为m。

1.2.1 坡地越障高度

纵向倾翻稳定角影响了履带在坡地跨越障碍物的最大高度。当履带式底盘处于临界平衡状态时，

[FNLb2-hCtan ρ+hC-rtGsin ρ-Lb2Gcos ρ]=0. （1）

当支撑力[FN=0]时，履带式底盘达到极限仰角：

[ρ=arctanLb2hC-rd]. （2）

此时台阶高度[Hb]与设计的整机结构参数之间存在以下关系：

[HbhC=Lb2+rdtan ρ2-hCtan ρ⋅sin ρ] .（3）

在理论上，履带式底盘的最大越障高度不会超过履带张紧轮的半径。综上，履带式底盘能够跨越的障碍物高度为：

[Hb，max=minHb，rt]. （4）

代入本机参数计算，去除覆带厚度后，得到最大越障高度为150 mm。

1.2.2 坡地最大跨越壕沟宽度

最大跨越壕沟宽度[Wmax]与设计的整机结构参数之间存在以下关系，

[Wmax=mina+hCtanθh，b-hCtanθh]. （5）

履带式底盘所能跨过的最大壕沟宽度受其整机的重心位置和所在坡地的坡度角影响，且不超过履带接地长度的一半。

代入本机参数计算，得到最大跨越壕沟宽度为350 mm。

2 小型底盘坡面稳定性分析

履带式底盘机器人行走时，能否保持稳定是履带式机器人作业的关键性能之一[12]。履带式底盘在坡地上不随意滑动或者翻倒，保持在一个稳定的状态的性能叫做稳定性，分为横向稳定性、纵向稳定性和滑移稳定性。本节建立履带式底盘的坡地稳定性模型，研究其坡面稳定性能。

2.1 坡面横向稳定性

履带式底盘机器人在山地坡面上横向行走时，受到的作用力有左右两侧履带的支撑力[FNL]、[FNR]，地面的附着力[FfL]、[FfR]，竖直向下的重力[G]，根据受力条件建立如图4所示的横坡行走理论模型，其中，B为左右两侧履带之间的轨距；e为重心横向偏移距离。如果此时坡面角度正好为履带式底盘的横向倾翻临界角度，右侧履带的地面支撑力则为[FNR=0]。

由力学平衡方程可求出，

[FN=Gcosθh0.5B+e-GhCsinθhB]， （6）

式中：[FN=FNL+FNR].

履带式底盘不发生横向倾翻的条件为[FNR]≥0，因此，其坡面横向倾翻临界角为：

[θhC=arctan0.5B+ehC]. （7）

要求所设计的坡面横向倾翻临界角≥35°，而重心横向偏移距离为影响其坡面横向稳定角的显著因素。同时，由于实际作业中整机的布置使重心的位置产生偏差，会对其坡面横向极限倾翻稳定角产生影响。

因此，当实际安装机具时，要适当降低重心高度，并使重心位置尽可能接近理论位置处。

2.2 坡面纵向稳定性

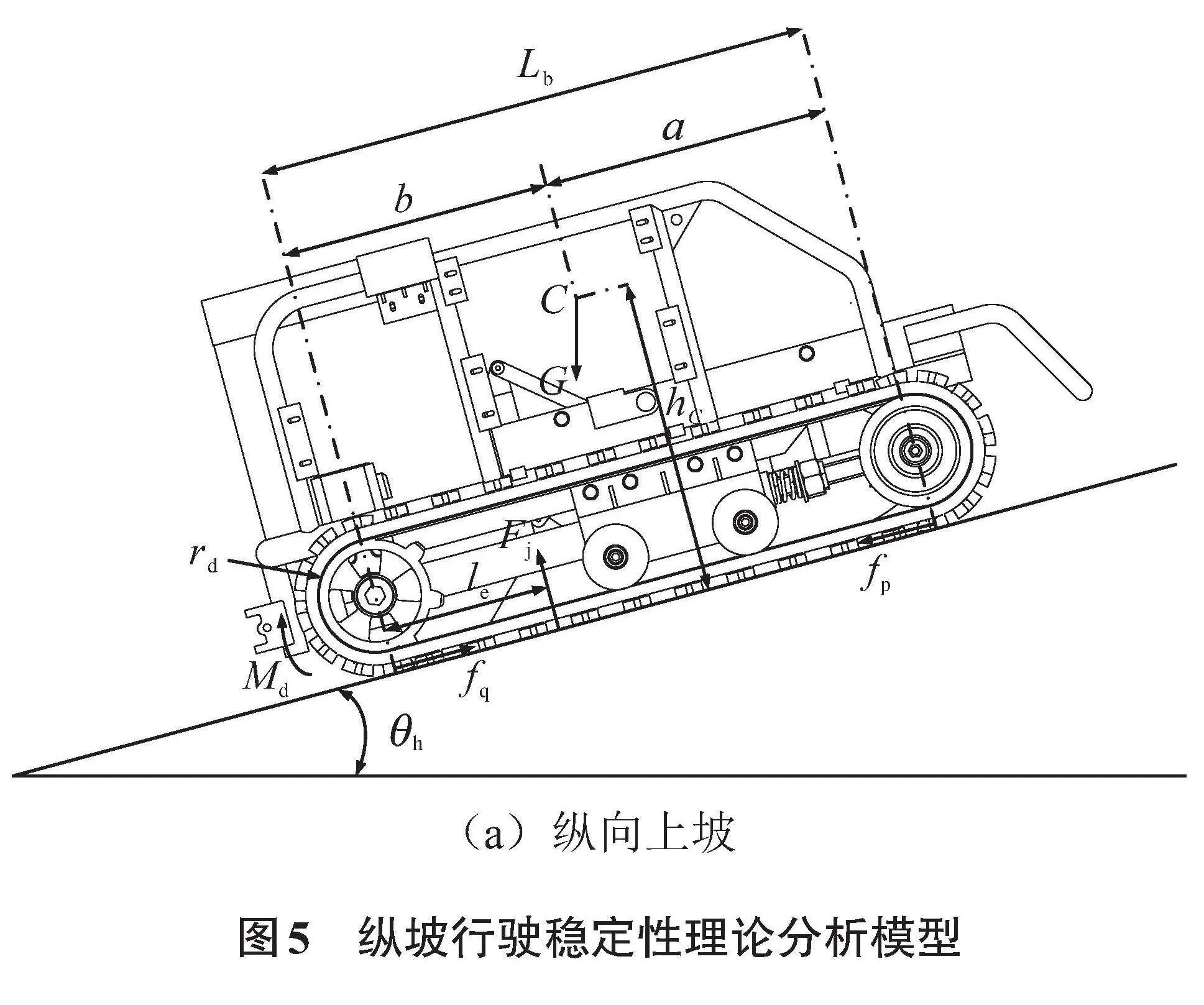
履带式底盘的坡面纵向稳定性能分为履带式底盘纵向上坡和纵向下坡2种情况[13]。根据履带式底盘机器人爬坡时受到的力（履带接触面受地面均布荷载的集中力[Fj]、牵引力[fq]，行走阻力fp）及地面支撑力与履带支撑面旋转边缘的距离（le），建立如图5所示的纵向爬坡理论模型。

研究纵向爬坡情况，如图5（a）所示，建立受力平衡方程：

[Gcosθh=Fj，Fjle-Gbcosθh+GhCsinθh=0.] （8）

在履带式机器人纵向爬坡的工况下，[le≥0]时整机不发生倾翻，此时履带式底盘爬坡时的倾翻稳定角为

[θhd=arctanbhC]. （9）

如图5（b）所示，履带式机器人在纵向下坡时：

[Gcosθh=Fj，Fjle+GhCsinθh-Gacosθh=0.] （10）

纵向下坡的极限倾翻稳定角：

[θhd=arctanahC]. （11）

在实际工况下，履带式底盘的重心并不在理论重心处，受到整机布置的影响，存在一定的偏移量，所以履带式底盘的纵向极限倾翻稳定角应为其2种工况下极限倾翻稳定角的最小值，即

[θhd=minθhd， θhd]. （12）

由理论计算可知，在实际作业中，整机重心离地面越低越不容易发生倾翻。因此，在实际安装机具时，要适当降低重心高度，并使重心位置尽可能接近理论位置处。

2.3 坡面滑移稳定性

坡面滑移稳定性是指履带式底盘机器人能平稳停靠在坡面上而不会下滑的能力，其在坡面静止而不产生滑移的条件为

[Ff=μsGcosθh≤Gsinθh，] （13）

式中：[Ff]为履带与地面的摩擦阻力；[μs]为履带与地面的附着系数。

履带式底盘机器人稳定地停在坡面上不产生滑移的最大坡度角为：

[θh≤arctanμs]. （14）

3 履带机构方案设计

3.1 电动机选取

所设计的履带式动力底盘机器人适用于丘陵山地，作业工况主要为平地和爬坡，其行驶阻力包括运行阻力、坡道阻力、转向阻力和内部阻力等。对履带式底盘在不同工况下所需的牵引力进行分析可知，坡地起步时其所需牵引力最大[14]，此工况下所需的牵引力为

[FT=λdcosθh+sinθh+0.03+amg，] （15）

式中：[FT]为履带式底盘所需牵引力，单位为N；[λd]为运行阻力系数，由试验确定；m为履带式底盘整备质量，单位为kg；g为重力加速度，取9.8 N/kg；[a∈0.01， 0.02]。

单侧驱动电机所需功率为

[P≥FTvm2ηx]， （16）

式中：[P]为驱动电机额定功率，单位为kW；[vm]为履带式底盘机器人行走速度，单位为m/s；[ηx]为行星减速器效率，取0.9。

驱动电机所需额定转速为

[n=vmi2πr×60]， （17）

式中：[n]为驱动电机额定转速，单位为r/min；[i]为行星减速器传动比，综合考虑，取[i]=24[15]；r为驱动链轮半径，单位为m。

驱动电机所需额定转矩为

[T=9 550Pn]， （18）

式中：[T]为驱动电机额定转矩，单位为N·m。

根据式（16）计算得出单个驱动电机所需功率约为395 W，所需额定转矩约为1.65 N·m。考虑功率储备，选用一款直流无刷伺服电机，额定功率为785 W，额定转速为3 000 r/min。

3.2 履带参数选取

设计的履带式底盘机器人作业环境较为复杂，对行走机构的附着能力和抗沉陷能力提出了一定的要求。履带式结构紧凑，相比轮式和腿式结构具有负重能力强、与地面接触面积大、下陷深度低、越野性能强等优点，所以底盘采用履带式结构。根据履带的设计参数，选用履带的节距[t0]为

[t0=bm4]， （19）

式中：[b∈15.0， 17.5]。

履带板工作条件所要求的平均接地比压决定了履带宽度[Kb]和履带支撑面长度[lb]，宽度越大，接地比压越小，接地比压为

[p=G2lbKb]， （20）

式中：[p]为接地比压，单位为Pa。

履带支撑面长度[lb]应满足转向要求，

[lbB≤1.85×ϕ-fμmax]， （21）

式中：[ϕ]为牵引附着系数；[f]为滚动阻力系数；[μmax]为最大回转阻力系数。

根据计算结果，最终选用轮孔式橡胶履带，驱动链轮的轮齿通过和履带上的齿孔进行啮合使得底盘获得行走动力。

3.3 驱动链轮参数设计与仿真

驱动链轮是驱动电机和履带之间的关键中间件，可将驱动电机的输出扭矩转化为履带式底盘运动的驱动力。履带驱动链轮的布置采用后置式布置，能够有效减少履带驱动段的长度，以及因为履带变形而产生的地面摩擦阻力，提高传动效率[16]。设计驱动链轮齿数[nq=7]，驱动链轮参数如下：

驱动链轮分度圆直径为

[D0=t0nqπ]. （22）

驱动链轮根圆直径为

[Dg=Ddrive-2LF]， （23）

式中：Ddrive为初步计算的齿轮齿根圆直径；[LF]为在履带内表面中内嵌线纤维中心的距离，[LF]=5 mm。

驱动链轮顶圆直径为

[Dd=D0+2δH-5，] （24）

式中：[δH]为履带厚度，查阅履带选型手册得[δH]=10 mm。

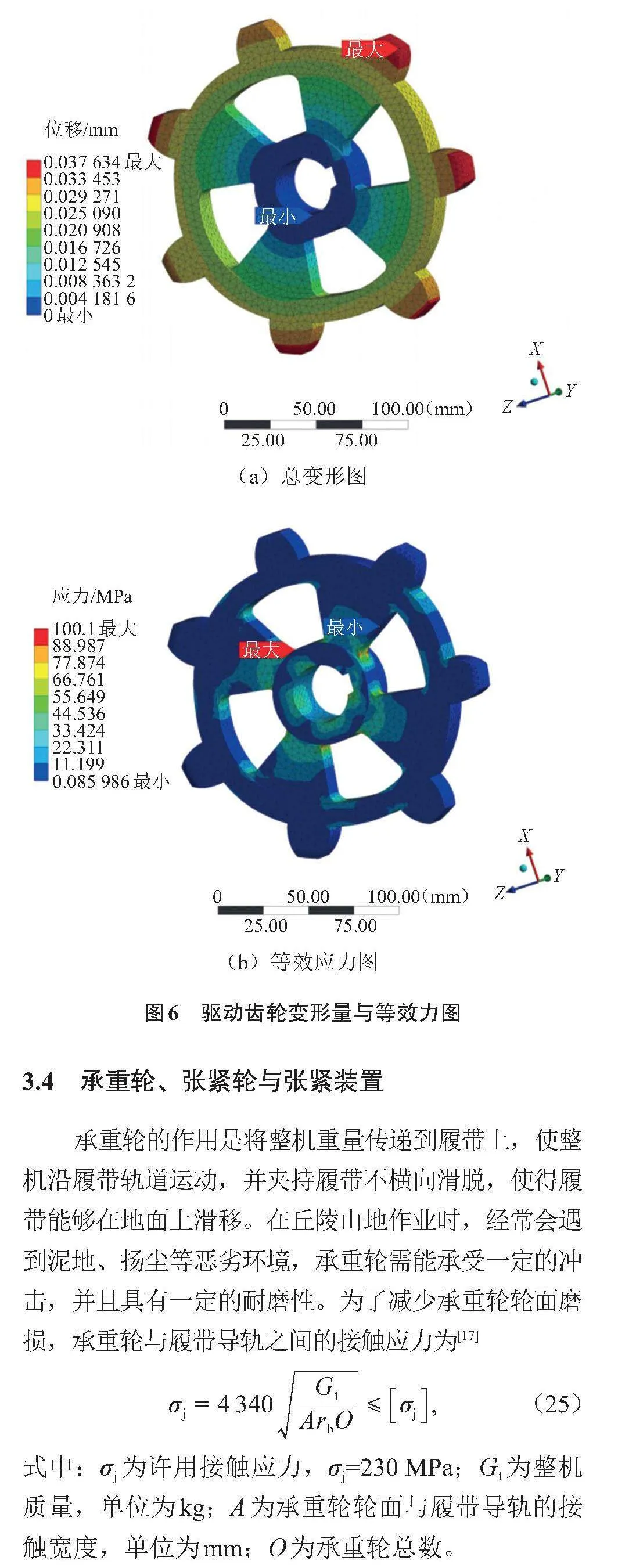
根据驱动链轮在坡地起步时受到的驱动扭矩，建立ANSYS有限元模型，分析驱动链轮在加载外载荷下的变形效果。最大变形量为0.037 6 mm，满足工况要求，最大等效应力为100.1 MPa，小于其材料的屈服强度，驱动齿轮变形量与等效力图如图6所示。

3.4 承重轮、张紧轮与张紧装置

承重轮的作用是将整机重量传递到履带上，使整机沿履带轨道运动，并夹持履带不横向滑脱，使得履带能够在地面上滑移。在丘陵山地作业时，经常会遇到泥地、扬尘等恶劣环境，承重轮需能承受一定的冲击，并且具有一定的耐磨性。为了减少承重轮轮面磨损，承重轮与履带导轨之间的接触应力为[17]

[σj=4 340GtArbO≤σj，] （25）

式中：[σj]为许用接触应力，[σj]=230 MPa；[Gt]为整机质量，单位为kg；A为承重轮轮面与履带导轨的接触宽度，单位为mm；[O]为承重轮总数。

履带在运动中会产生振跳现象，履带的振跳会引起冲击、振荡和额外的功率消耗，加速零件磨损。张紧轮和张紧装置能够使得履带保持一定的张紧度，在一定程度上减少这种现象。履带张紧后，也可以避免其在作业时脱落。张紧轮是张紧装置的组成成分，通过它引导履带正确卷绕。张紧装置的调整方式采用螺杆调整，通过调节螺杆和螺母来改变张紧轮的位置，达到张紧的目的，其结构简单，具有一定强度和刚度。在履带运行受到冲击时，螺杆的调整不具有缓冲作用，而在螺杆上加入弹簧之后，就能够有效地减少冲击，张紧力[Tz]为[18]

[Tz=GvLq24he]， （26）

式中：[Gv]为履带单位长度的重力，单位为N/mm；[Lq]为张紧轮与驱动轮之间的中心距，单位为mm；[he]为履带的最大悬垂度，单位为mm。

3.5 机架设计及仿真

机架需要能承受来自履带行走系统和其他作业结构受到振荡时的冲击，其结构设计方案以及布置方式显得尤为关键[19]。综合考虑本文设计的履带式底盘整机布置要求，采用履带主体框架放置在两边、机架安装在中间的方式，保证机架的中间位置能够布置作业机构。上车的支撑框架采用钢结构式框架，主体采用Φ25 mm×4 mm与Φ38 mm×5 mm的钢管焊接而成，在保证整体刚度的同时降低加工难度，且在整机倾翻后能有效保护其内部设备不受损坏。

利用有限元软件ANSYS Workbench对车架进行静力学分析，以确保机架能够具有足够的承载能力。定义材料为Q235碳素结构钢，密度为7.85×[10-6] [kg/mm3]，弹性模量为2.01×[105] [MPa]，泊松比为0.3，拉伸屈服强度为235 MPa，极限拉伸强度为420 MPa。

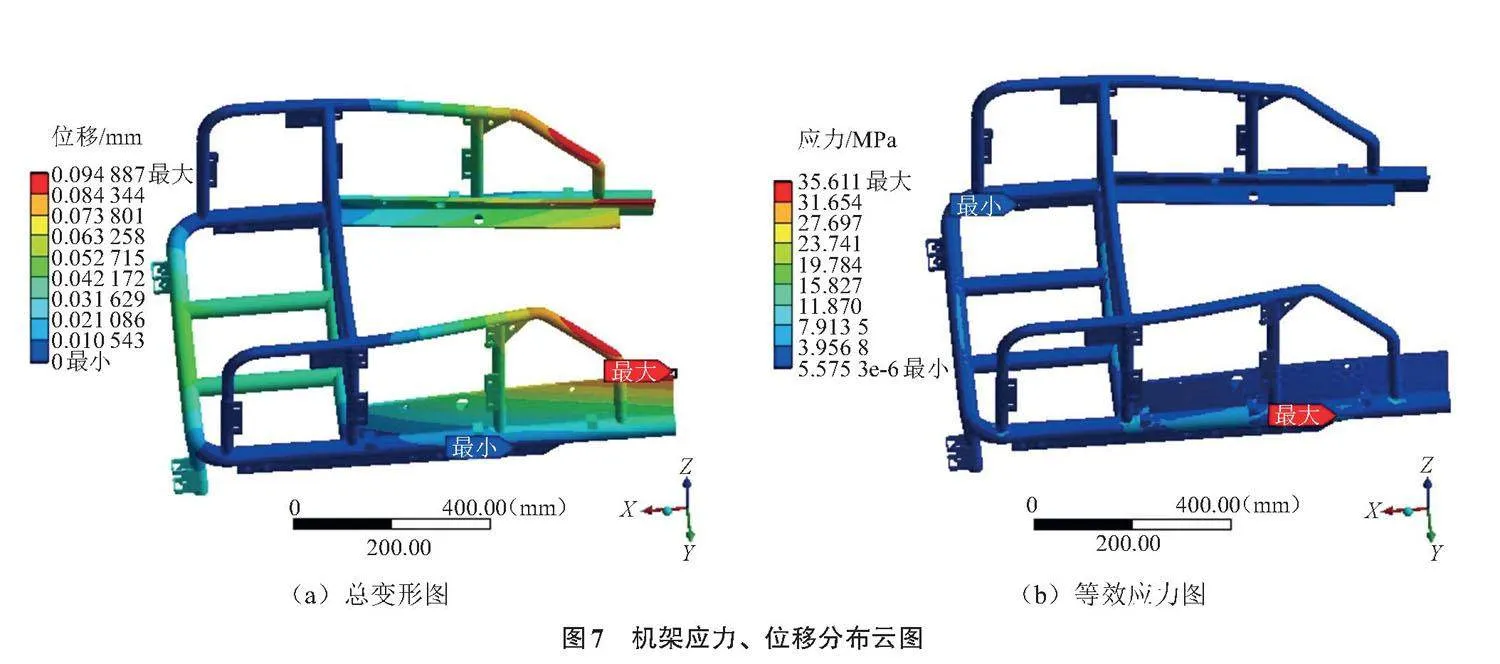
根据各部件的质量和位置分布，定义机架各部分所受到的载荷。机架两端安装履带，中间承受作业机构的重量，后方背负电池组，在相对位置分别施加作用力，分析得到的机架应力、位移分布云图如图7所示。最大应力为35.611 MPa，出现在机架与履带连接处，满足强度要求；最大形变量为0.094 8 mm，满足刚度要求。

4 履带式底盘动力学模型的建立与分析

4.1 几何模型的建立

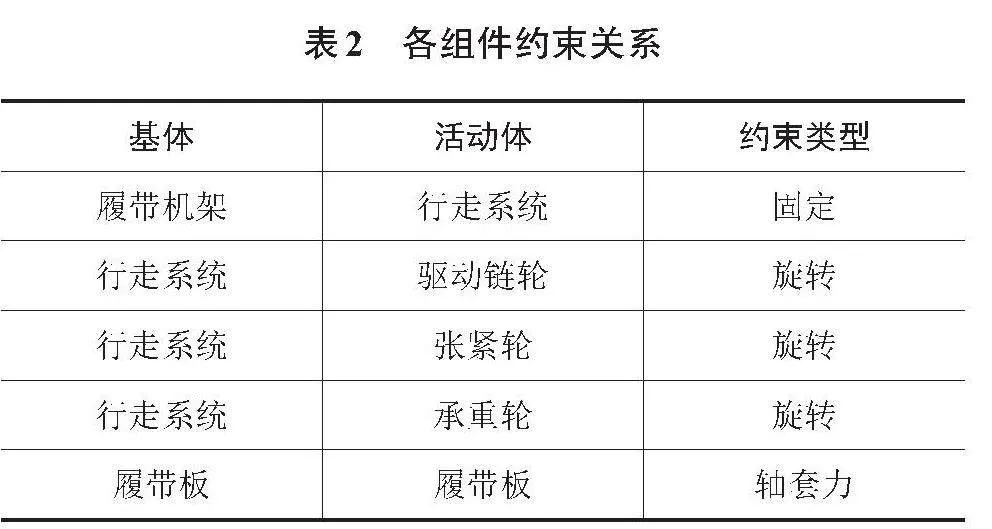
在建立几何模型时，通常对履带式底盘做简化处理，将电机、减速器、机架简化为一个刚体，这时履带式底盘可简化为主体和履带行走机构。运用UG软件对主体进行三维建模，以左张紧轮轴向外侧为坐标轴轴心，履带布置方向为x轴方向，张紧轮位置指向驱动链轮位置为x轴正轴，左张紧轮轴线为y轴方向，指向右张紧轮方向为y轴正轴，履带式底盘垂直指向机架位置为z轴正向，建立坐标系，为履带底盘每个零件分别赋予相应材料，测量其重心坐标为（232， 506， 152）；之后导入RecurDyn软件中，采用RecurDyn软件低速履带模块（Track-LM）建立履带行走机构，两侧履带行走机构分别包括1个驱动链轮、2个承重轮、1个张紧轮、1个履带机架和1条履带，对各组件之间添加约束，具体如表2所示。

4.2 路面模型的建立

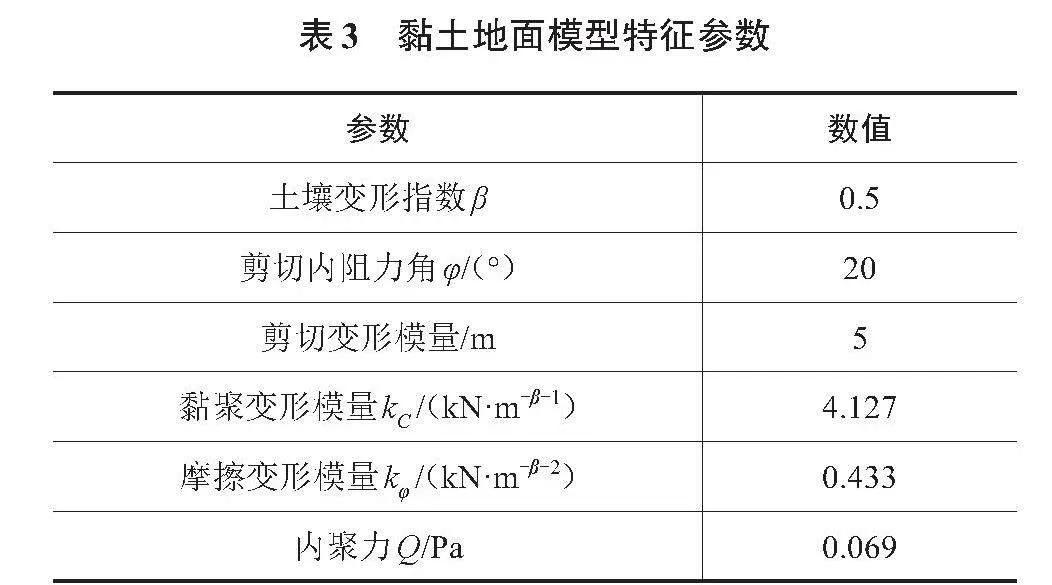
RecurDyn软件提供地面参数Ground模块，根据经典土壤力学理论，本文采用其中的黏土（clayey soil）地面模型，其路面特征参数如表3所示。

4.3 模型驱动设置

为了使丘陵山地模块化小型机器人行走系统能够工作，需要对履带行走机构添加驱动函数，选择STEP函数作为驱动函数添加在驱动链轮的旋转副上，

[STEP（t，t0，h0，t1，h1）]， （27）

式中：[t]为自变量；[t0]、[t1]分别为自变量的初始值与终止值，即仿真开始与结束的时间，根据仿真内容的不同更改[t0]、[t1]的数值；h0、h1为设计变量的初始值与终止值，选择角速度作为设计变量。

4.4 履带式底盘动力学模拟仿真

根据前文理论分析计算所得到的驱动电机最大转矩，探讨履带式底盘机器人的最大爬坡角度与最小转向半径。

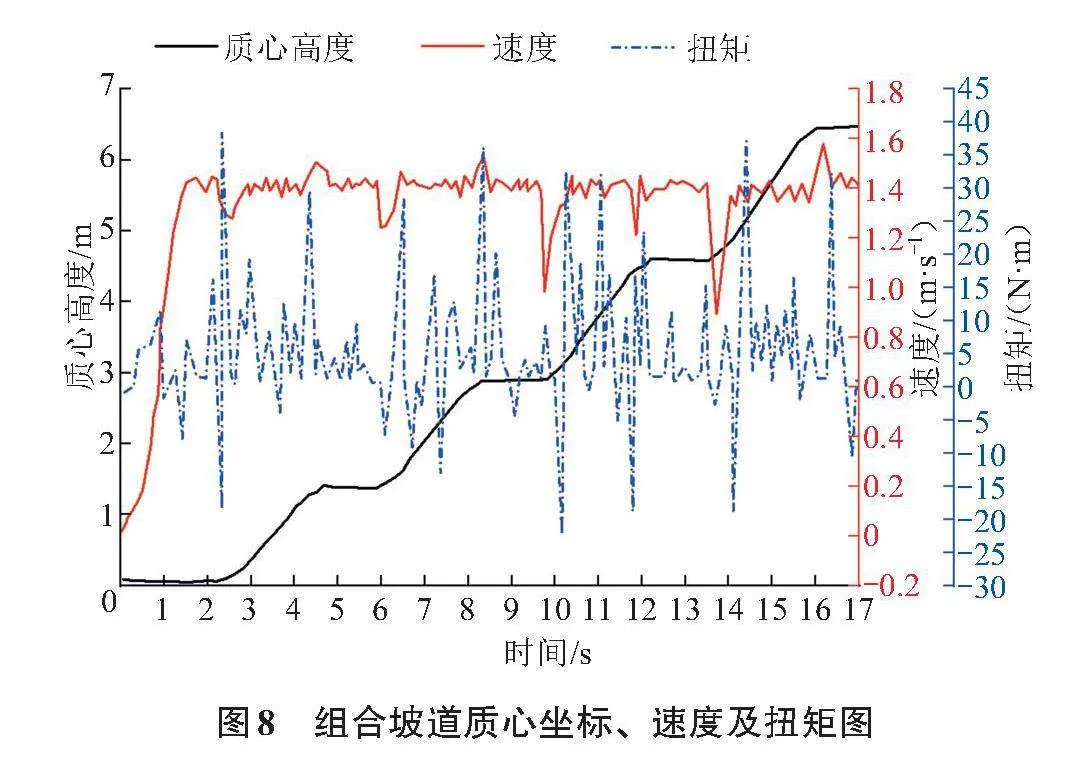
1）根据履带式底盘机器人爬坡路面的特点，软件中路面宽度设定为1 700 mm，通过Ground模块建立25°、28°、31°、34°组合坡道，在驱动链轮旋转副添加驱动角速度，具体如下：STEP（t， 0， 0， 1.5， 20.0）。

仿真所得到的履带式底盘组合坡道质心Z坐标位移、速度与扭矩如图8所示，红色实线为履带式底盘质心Z坐标变化曲线，黑色实线为履带式底盘速度变化曲线，点划线为履带扭矩随时间变化的曲线图。在0～1.5 s内，履带转速由0增加至20 rad/s，1.5 s后，履带以1.78 m/s匀速行驶，扭矩波动范围不大。2.0 s后开始爬坡，此时履带式底盘质心升高，速度出现短暂的波动后稳定下来，扭矩值增加，最大值为39.8 N·m，到4.5 s时爬坡完成，扭矩也基本稳定。当履带式底盘机器人开始爬坡动作时，速度会下降，在13.5 s时，速度达到最低1.06 m/s，扭矩在此之后增加，在第16.0 s时完成爬坡动作，34°爬坡成功。

2）平地转向路面长度和宽度均设定为4 000 mm，通过Ground模块建立地面，在驱动链轮旋转副添加驱动角速度，具体如下：STEP（t， 0， 0， 1.5， 20.0）、STEP（t， 0， 0， 1.5， -20.0）。

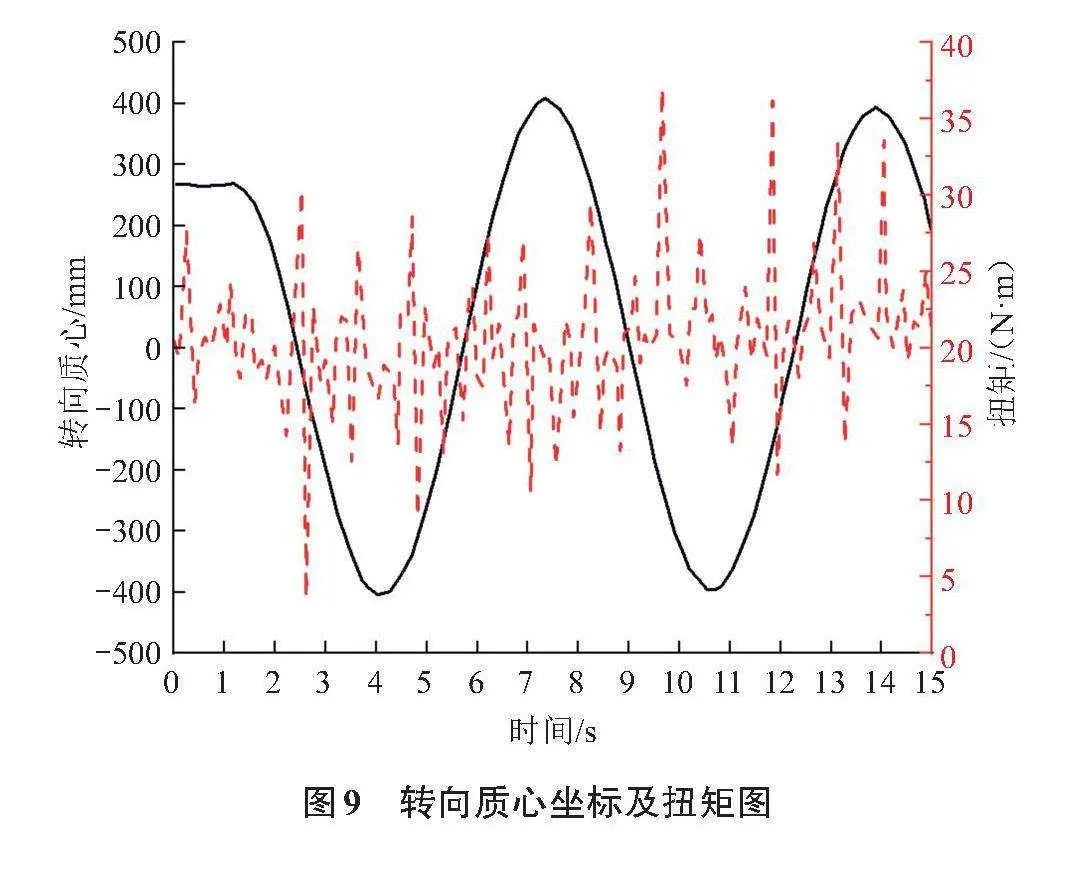
3）在标准路面转向时，底盘双侧履带差速制动，使得转弯半径达到最小值。其单侧履带驱动扭矩的最大值为38.7 N·m，扭矩均值为19.8 N·m，转弯半径在407.0 mm，如图9所示。

5 样机试验

根据上述计算与仿真结果，为验证履带式底盘机器人爬坡、转向与越障性能是否符合预期设计要求，根据《农业机械生产试验方法》（GB/T 5667—2008）[20]，研制样机并进行行驶速度、转弯半径、爬坡角度与越障高度试验，样机如图10所示。

5.1 试验方法与结果

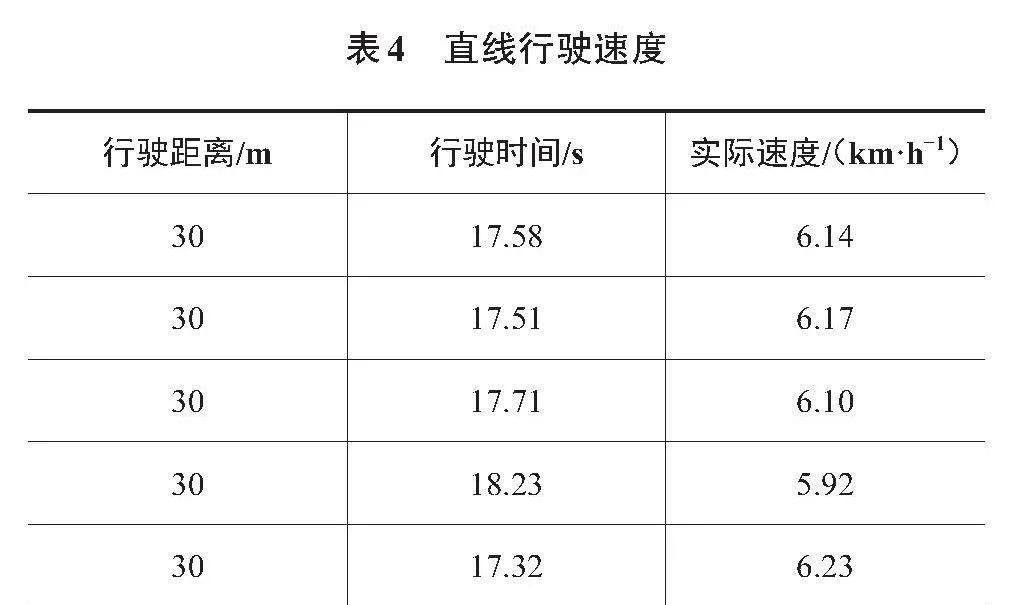
1）行驶速度：通过遥控手柄控制履带在长度为30 m的水泥平地直线行驶，测定样机通过测定区间所需时间，重复5次，计算最大行驶速度。直线行驶速度试验结果如表4所示，平均速度为6.11 km/h。

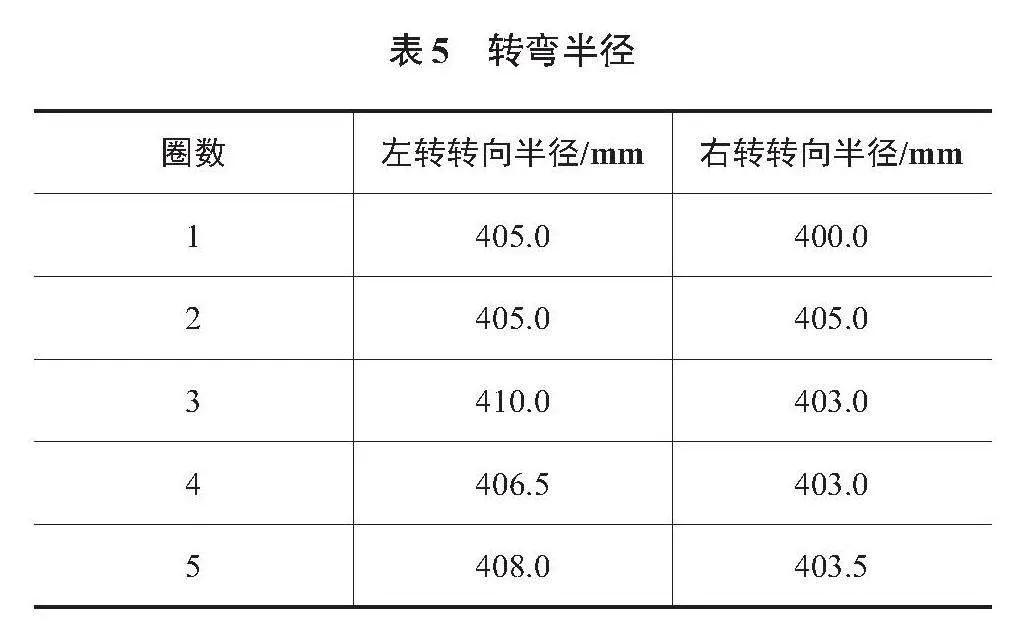
2）转弯半径：遥控样机，使其以5.00 km/h的作业速度在草地上执行转向指令，一侧驱动链轮制动，另一侧驱动链轮前进，重复差速转向半径试验5次，利用钢尺测量履带在地面留下的轨迹圆半径。试验结果如表5所示，最小转弯半径为403.0 mm。

3）爬坡角度：搭设简易坡台，模拟草地爬坡坡道，设置坡台初始角度为25°，之后每次试验增加3°，直至样机无法驶上坡道。测量得出最大爬坡角度，当爬坡角度为38°时开始出现滑移现象。

4）越障高度：在平地进行越障试验，根据所计算的坡地越障高度分析，搭建越障台阶。以匀速作业速度跨越障碍物台阶，直至无法跨越为止。根据越障试验可知履带式底盘机器人最大越障高度为170 mm。

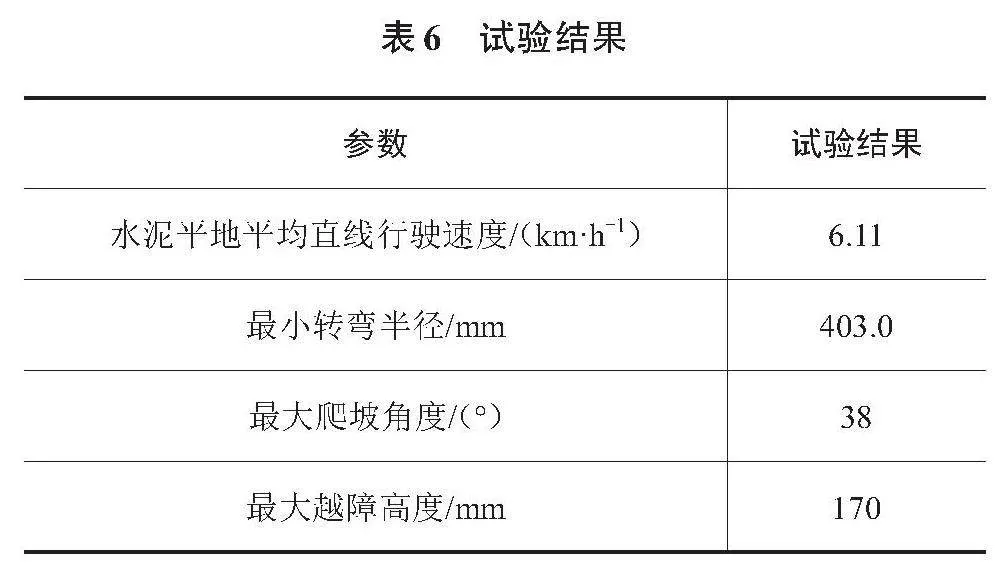
5.2 试验结果分析

试验结果如表6所示，结果表明，小型模块化履带式底盘在水泥平地上的平均直线行驶速度为6.11 km/h；最小转弯半径为403.0 mm；最大爬坡角度为38°，略大于所设计的爬坡角度，这与样机的重心布置产生的偏移有关。实际样机的重心较为接近理论值，且试验坡台与草地对履带表面之间的摩擦系数有所不同，实际工况下爬坡角度会有一定差异。最大越障高度为170 mm，理论最大越障高度略小于试验值，出现这一情况的原因在于橡胶履带表面结构增加了履带与障碍物之间的附着系数。

6 结论

针对我国丘陵山地经济作物种植园区非结构化的地形条件以及种植作物采收多样性问题，本文设计了一款小型履带式动力底盘。首先，结合我国相关的农机农艺要求，提出丘陵山地履带式动力底盘的设计要求，确定整机结构组成与系统布置，对履带式底盘的稳定性和通过性进行研究；其次，对驱动系统进行设计，选取履带与电动机参数并对驱动轮以及机架进行有限元分析；再次，通过建立虚拟样机模型，对履带式底盘爬坡工况进行仿真分析；最后，依据计算参数试制了实体样机，并设计和进行了整机的性能试验。结论如下：

1）根据丘陵山地作业对动力底盘的作业要求，完成了履带式底盘的结构设计和布置。

2）对履带式底盘的通过性和稳定性进行分析可知，重心对坡面横、纵向稳定性影响较大，在坡面行走时，履带式底盘会发生滑移而不发生倾翻。

3）建立动力学模型，对爬坡与转向工况进行仿真分析，得到履带在不同工况下驱动链轮所需的驱动转矩、速度与质心曲线，证明履带式底盘运行平稳，工作可靠。

4）对履带式底盘机器人进行试制与整机性能试验。通过经济性测试可知，履带式底盘机器人平均直线行驶速度为6.11 km/h，最小转弯半径为403.0 mm，最大爬坡角度为38°，最大越障高度为170 mm，满足使用要求。

参考文献

[1] 孙景彬，刘志杰，杨福增，等.丘陵山地农业装备与坡地作业关键技术研究综述[J].农业机械学报，2023，54（5）：1-18.

[2] 罗锡文.对发展丘陵山区农业机械化的思考[J].农机科技推广，2011（2）：17-20.

[3] 姬江涛，郑治华，杜蒙蒙，等.农业机器人的发展现状及趋势[J].农机化研究，2014，36（2）：1-4，9.

[4] 刘平义，柯呈鹏，柯婷，等.丘陵山区农用预检测主动调平底盘设计与试验[J].农业机械学报，2020，51（3）：371-378.

[5] 曾俊豪，高巧明，黄贵东，等.一种果园除草底盘设计与仿真[J].广西科技大学学报，2021，32（3）：53-59，66.

[6] 刘九庆，姚凯.履带式森林灭火炮转向性能分析与验证[J].森林工程，2021，37（3）：95-102.

[7] CHAJKIN A P，DOBRETSOV R Y，SOKOLOVA V A，et al.Mathematical model for assessing lateral stability of articulated tracked vehicles[J].Journal of Physics：Conference Series，2021，2094（4）：042005.

[8] DUDZINSKI P A，CHOLODOWSKI J.A method for predicting the internal motion resistance of rubber-tracked undercarriages，Pt.1：a review of the state-of-the-art methods for modeling the internal resistance of tracked vehicles[J].Journal of Terramechanics，2021，96：81-100.

[9] 扈凯，张文毅，李坤，等.高地隙三角履带底盘多体动力学建模与试验[J].农业机械学报，2021，52（7）：386-394.

[10] 谢京玮，谌炎辉，郑特.多特征复杂零件的模块化设计[J].广西科技大学学报，2020，31（4）：97-103.

[11] 韩振浩，朱立成，苑严伟，等.山地果园履带底盘坡地通过性能分析与优化设计[J].农业机械学报，2022，53（5）：413-421，448.

[12] 潘冠廷，杨福增，孙景彬，等.小型山地履带拖拉机爬坡越障性能分析与试验[J].农业机械学报，2020，51（9）：374-383.

[13] 何维山，唐俊，宋正辉.某山区公路碎石土滑坡成因及稳定性分析[J].广西科技大学学报，2021，32（4）：100-103.

[14] BROOKS C P.The automotive chassis：engineering principles[J].Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，2002，216（8）：707.

[15] 朱双霞，张红钢.机械设计基础[M].重庆：重庆大学出版社，2016.

[16] 唐经世.工程机械底盘学[M].成都：西南交通大学出版社，2002.

[17] 诸文农.底盘设计[M].北京：机械工业出版社，1981.

[18] 杨敬伟.履带底盘导向张紧装置型式研究与设计应用[J].机械传动，2013，37（5）：114-116.

[19] 叶燕帅，傅爱军，陈钊炎，等.基于HyperWorks的巴哈赛车车架仿真与优化研究[J].广西科技大学学报，2023，34（3）：14-19.

[20] 全国农业机械标准化技术委员会.农业机械 生产试验方法：GB/T 5667—2008[S].北京：中国标准出版社，2008.

Design and testing of a small tracked powered chassis for hilly

mountainous terrain

CAI Yuchen1， GAO Qiaoming*1， 2， LUO Yueyang1， MI Zerong1， LI Zongpeng1， LYU Pan1

（1. School of Mechanical and Automotive Engineering， Guangxi University of Science and Technology， Liuzhou 545616， China; 2. Huilaibao Machinery Manufacturing Co.， Ltd.， Hepu County， Beihai 536100， China）

Abstract： Aiming at the unstructured terrain of Guangxi hilly and mountainous planting areas for economic crops and the complex growing environment of various crops， a small tracked power chassis with high mobility and adaptable to the hilly and mountainous terrain is designed. This paper takes the crawler chassis as the research object， establishes the crawler chassis slope walking model， researches its stability and passability when climbing slopes， and puts forward the chassis design scheme and parameter selection. Based on ANSYS Workbench， the force analysis of the frame is carried out， with the maximum displacement deformation of the frame 0.094 8 mm， and the maximum equivalent force 35.611 MPa， which meets the requirements of strength use. The virtual modeling of the crawler chassis is carried out using RecurDyn dynamics simulation software to analyze the changes of the center of mass and torque of the chassis in the process of climbing and steering， which verifies the feasibility of the scheme. The results of the field test show that the crawler chassis has a straight line traveling speed of 6.11 km/h on the concrete flat ground， the minimum turning radius of 403.0 mm， the maximum climbing angle of 38° on the grass， the maximum height of 170 mm over the obstacle， and the chassis runs smoothly during the operation. The parameters of the crawler chassis designed can meet the requirements of the whole machine design， and the operation indexes meet the requirements of the relevant standards， and it has good performance of climbing and crossing obstacles， and the research results can provide a reference for the design and development of the crawler chassis in hilly and mountainous areas.

Keywords： hilly mountainous terrain; tracked undercarriage; agricultural machinery; RecurDyn

（责任编辑：于艳霞，黎 娅）

收稿日期：2023-09-08；修回日期：2023-10-11

基金项目：中央引导地方科技发展资金项目（桂科ZY22096023）；广西科技计划项目（桂科AB21220058）资助

第一作者：蔡羽晨，在读硕士研究生

*通信作者：高巧明，博士，高级工程师，硕士生导师，研究方向：农业机械化关键技术与装备、图像模式识别，E-mail：walkergao@163.com