高效混合预测策略的设计

摘 要：现有的分支预测模型无法完全准确预测处理器中各种指令的行为，导致处理效率受限。为此提出了两种混合预测解决方案，旨在结合多种分支预测模型，以提高预测的准确性和处理器的执行效率。将TAGE（tagged geometric history length）分支预测模型与BATAGE（Bayesian tagged geometric history length）分支预测模型的预测结果转交Hybrid模型。在预测阶段中，Hybrid模型会根据TAGE和BATAGE的历史表现去选择表现最佳分支预测模型的预测结果。而在更新阶段中，Hybrid模型会根据设计的混合预测策略对需要更新条目的饱和计数器进行更新。在CBP（championship branch prediction）软件仿真平台提供的440个测试程序上进行实验，实验结果表明：与多种最新主流分支预测模型相比，两种混合预测解决方案的预测错误率均低于它们。该研究为预测所有指令模式行为问题提供了有效解决方案。在实际CPU的分支指令预测，该研究提供了一些实用价值。

关键词：TAGE；BATAGE；分支预测；混合预测

中图分类号：TP332 文献标志码：A 文章编号：1001-3695（2024）09-028-2766-07

doi：10.19734/j.issn.1001-3695.2023.12.0641

Design of efficient hybrid predicting strategies

Fang Xinyu1，Zhou Rigui1，Gong Mingqing2

（1.College of Information Engineering，Shanghai Maritime University，Shanghai 201306，China;2.Hangzhou Today’s Headlines Technology Co.，Ltd.，Hangzhou 311100，China）

Abstract：The existing branch prediction models can’t predict the behaviors of various instructions in the processor accurately，which leads to the limitation of processing efficiency.Therefore，this paper proposd two hybrid prediction solutions，which aimed to combine multiple branch prediction models to improve prediction accuracy and processor execution efficiency.This paper transferred the prediction results of TAGE branch prediction model and BATAGE branch prediction model to the Hybrid model.In the prediction phase，the Hybrid model selected the prediction results of the best-performing branch prediction model based on the historical performance of TAGE and BATAGE.In the update phase，the Hybrid model updated the saturation counter of the entries that needed to be updated according to the designed hybrid prediction strategy.Experiments on 440 test programs provided by the CBP software simulation platform show that the prediction error rates of both hybrid prediction solutions are lower than those of many of the latest mainstream branch prediction models.This study provides an effective solution to the problem of predicting all command mode behaviors.In the branch instruction prediction of real CPU，this research provides some practical value.

Key words：TAGE;BATAGE;branch prediction;hybrid prediction

0 引言

分支预测是计算机体系结构领域中的一个重要研究主题，尤其是在高性能处理器设计方面。现代中央处理器［1］都广泛采用分支预测技术［2］，其主要目的是预测程序中的控制流路径，以减少由于分支指令引起的处理器流水线中的延迟和中断。在分支预测的研究中，最常见的挑战包括减少条件分支指令的错误预测来提高预测准确性。然而，目前的分支预测模型都无法精准预测所有类型的条件分支指令。针对这个问题，国内外研究人员在过去十几年作出诸多贡献：在处理器设计的早期阶段，简单的静态预测策略得到了广泛应用。随着计算需求加深，动态预测技术［3］逐渐成为主流，如二级自适应训练分支预测模型（Bimodal［4］，Gshare［5］）、高精度条件分支预测模型TAGE［6］及其优化模型［7～9］、以及结合多个分支预测模型的混合预测模型［10］。此外，还有尝试利用神经网络模型［11］来捕捉更复杂的分支行为。在实际应用上，学术界［12，13］在Sonic Boom开源IP核中应用了分支预测模型，工业界［14，15］在具体产品也中也应用了分支预测技术。

为了尽可能预测大多数条件分支指令，主要方案包括基于传统TAGE分支预测模型的优化；引入具有强大学习能力的网络模型［16，17］；组合不同预测模型的混合预测［18］，能够利用各个预测模型特点，提升预测精度并适应各种分支指令行为。本文旨在结合两种分支预测模型并且设计混合预测策略，以提高预测准确性，适应更多应用测试场景。最新提出的混合预测模型采用BATAGE与无偏差神经网络预测模型相结合［19］，虽然提高了预测准确度，但是需要较长时间训练模型才能达到理想效果。

本文将TAGE与BATAGE［20］分支预测模型相结合，并且设计混合预测策略来提高预测准确性。如何得到最终预测结果是需要考虑的问题。所以，本文设计适应性增减策略和权重策略两种混合预测策略方案。通过利用两种分支预测模型的预测结果和混合预测策略，得出最终预测结果。混合预测策略采用单独载体接受TAGE和BATAGE的预测结果，这里称为Hybrid预测模型，其本身为标记预测表。在混合预测策略中，适应性增减策略考虑全部历史信息模式行为对当前决策的影响；而权重策略更加注重考虑近期历史信息模式行为对当前决策的影响，削弱早期历史信息模式行为的影响。在预测方面上，两种混合预测策略都是选择历史表现最好预测模型的预测结果。在更新方面上，适应性增减策略是在需要更新的条目上自增或自减；权重策略是在需要更新的条目上采用指数平滑法。

1 预测模型及预测模型架构介绍

1.1 TAGE分支预测模型

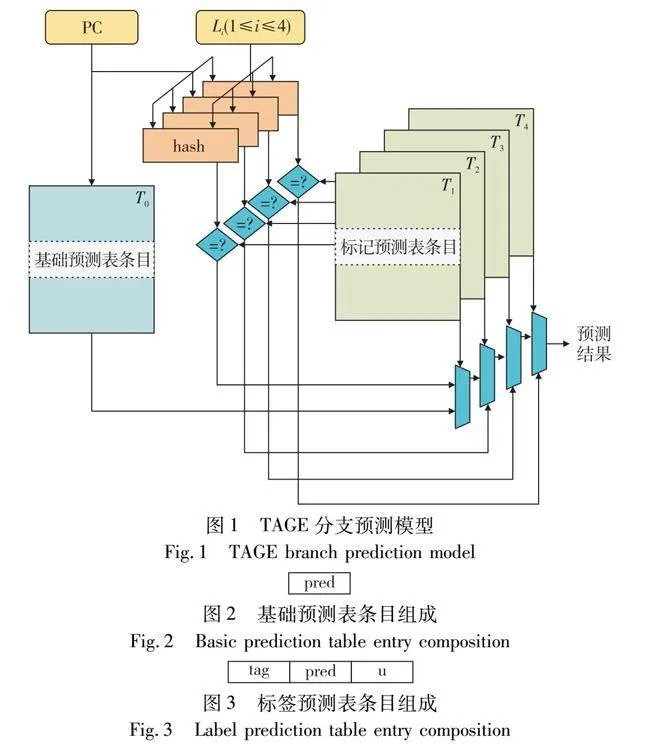
TAGE分支预测模型结构如图1所示，由一张基础预测表和四张标记预测表组成，分别用T0，T1，T2，T3，T4表示。基础预测表由多项条目组成，每项条目是用于预测的饱和计数器，标记预测表的每项条目由标签（tag）、预测位（pred）和评估置信度（u）三部分组成。基础预测表和标记预测表的条目组成如图2和3所示。

在TAGE分支预测模型中，每张标记预测表需要不同长度的分支历史信息来匹配条目的标签，其所需长度遵循

L（i）=（int）（αi-1×L（i）+0.5）（1）

其中：1≤i≤M，M表示标记预测表的数量。基础预测表用PC（program counter）来索引和匹配条目，匹配到条目所对应的饱和计数器负责提供预测结果。另外，标记预测表将PC与不同长度的历史信息进行哈希运算来完成标签匹配。若标签匹配成功，表明某张标记预测表命中，最终预测结果源自于成功匹配到所需最长历史信息的标记预测表。若所有标记预测表的标签都未能命中，则采用基础预测表的预测结果作为最终预测结果。

TAGE分支预测模型的更新策略主要针对更新条目的pred和u字段进行调整。这里引入provider和altpred的概念，分别表示匹配最长和次长历史信息预测表。u字段会根据是否准确预测进行调整：当provider和altpred不同时，它会递减，否则会递增。在文献［6］中，每256K分支指令都会定期重置u。对于provider，若TAGE分支预测模型预测准确，则更新provider的pred字段。相反，如果TAGE分支预测模型预测不正确并且provider不是所需最长历史信息的预测表，则不仅更新provider的pred字段，而且在比provider所需历史信息更长的预测表中分配新条目。新分配条目需要初始化：u字段初始化为0，pred字段初始化为weak correct。

1.2 BATAGE分支预测模型

BATAGE与TAGE分支预测模型结构相同，同样也是由基础预测表和标记预测表组成。BATAGE与TAGE分支预测模型结构不同主要在于引入贝叶斯置信度评估机制和条目分配受控分配机制替代原有TAGE的预测和更新机制，下面详细介绍BATAGE与TAGE分支预测模型结构的不同之处。

BATAGE条目组成：基础预测表T0条目组成如图2所示，由饱和计数器位所组成；标记预测表从T1到T4条目组成如图4所示，tag表示标签用于匹配，n1与n0记录条件分支指令的跳转和未跳转次数。BATAGE分支预测模型会通过n1与n0字段计算当前条目的错误预测率并且选择最终预测结果。

贝叶斯置信度评估机制应用在分支预测阶段，在BATAGE分支预测模型的预测阶段：

a）在基础预测表中，预测结果直接通过分支指令的PC值索引基础预测表中的条目获得。

b）在标记预测表中，通过条件分支指令的PC值与分支历史信息进行哈希运算，其结果去匹配标记预测表的标签，其中不同的标记预测表所需历史信息长度也是不同的。另外，BATAGE［20］分支预测模型所描述的贝叶斯置信度评估机制利用n0和n1字段来计算当前错误预测率qi。若错误预测率越低，则置信度越高。

c）若标记预测表都没有匹配成功，则采用基础预测表结果。反之，根据每张预测表得到的错误预测率qi，选取结果qi最小对应标记预测表的预测结果；若qi存在相等的情况，此时根据匹配成功的标记预测表所对应历史信息长度情况，选择历史信息长度最长对应标记预测表的预测结果。

条目分配受控分配机制应用在分支预测错误阶段，为每个错误预测的预测表都分配新条目不是最佳策略，过度分配会导致许多预测表的条目通过贝叶斯置信度评估机制，导致预测不够准确，进而导致分支预测模型缺乏足够多历史信息来提供准确预测。

其中心思想是比较NHC（中置信度/低置信度）的条目数量和MHC（适度高置信度）的条目数量，其中MHC介于特定范围内（文献［20］中为0.17～1/3）。监控MHC与NHC条目比例来调整分配概率，若其比例大于设定阈值，则增加分配概率，反之，减少分配概率。

1.3 分支预测模型缺陷

TAGE分支预测模型广泛应用于现代微处理器，以提高指令流水线处理效率。该模型采用非标记预测表加标记预测表的多表架构，每张标记预测表的哈希运算需要不同长度的历史信息，这能够捕获广泛的程序行为模式。通过在表中利用不同长度的历史信息，TAGE分支预测模型可以与分支指令行为最佳地保持一致。除基础预测表外，每个预测表条目都带有标签，这有助于区分所需不同长度的分支历史信息，以减少预测冲突和不准确。TAGE分支预测模型历史长度的几何级数确保了从短期到长期分支历史信息的覆盖，增强了预测的灵活性和准确性。

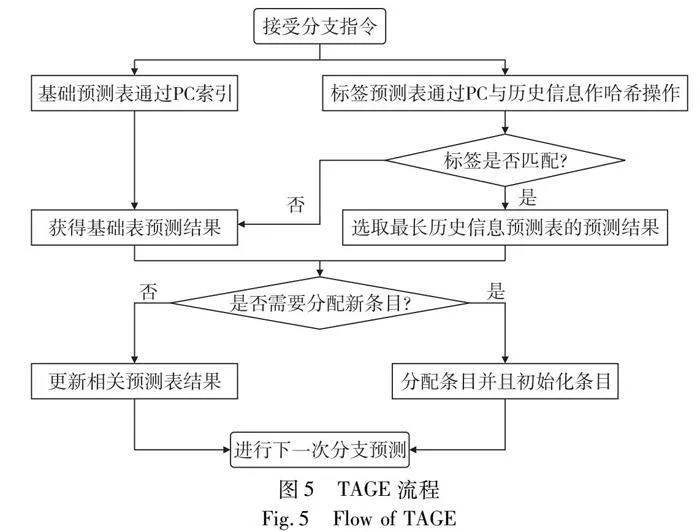
TAGE分支预测模型的流程如图5所示。尽管TAGE分支模型因高精度和适应性而受到青睐，但是存在一个称为冷计数器的问题：其中弱偏差分支指令需要大量训练，饱和计数器才能实现最佳预测能力。若跳转概率越大，那么计算错误概率趋于稳定的次数越多。

BATAGE分支预测模型以TAGE分支预测模型为基础，在不改变核心结构的情况下引入了多项关键修改。这些修改包括：a）标记预测表的条目新颖组合，用跳转发生次数（n1）和非跳跃发生次数（n0）的计数器替换原始预测（pred）和评估置信度（u）位；b）采用贝叶斯置信估计机制进行预测，而不是TAGE分支预测模型选择最长匹配历史信息对应预测表的预测结果；c）针对错误分配情况，创新受控条目分配机制，用于评估条目分配的必要性。基于以上三点，这些修改使BATAGE模型能够有效缓解冷计数器问题。

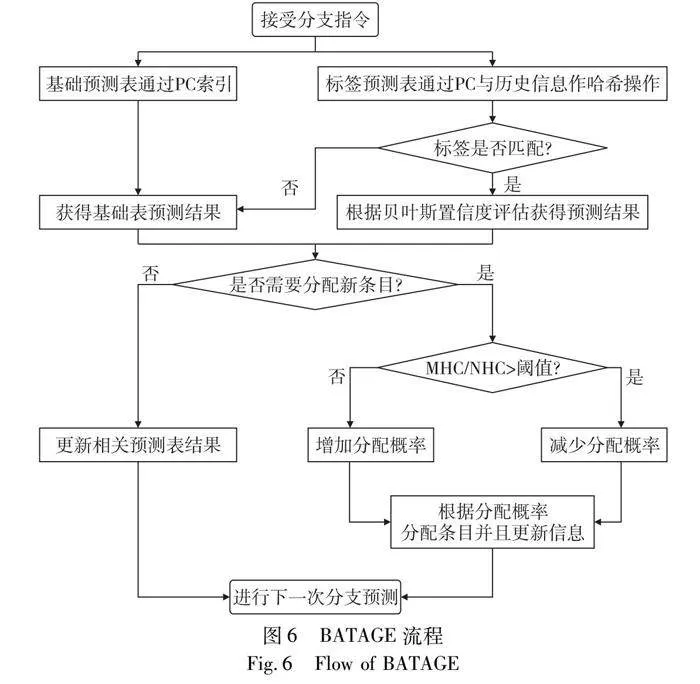
虽然引入贝叶斯置信度估计和受控条目分配机制缓解了冷计数器问题，但它还是存在某些限制：虽然这些机制赋予BATAGE分支预测模型对复杂分支指令行为的卓越预测能力，但比TAGE分支预测模型更加复杂。BATAGE分支预测模型具体流程如图6所示。从图6可知，预测阶段不再是选取成功匹配到最长历史信息标记预测表的预测结果，而是先选取错误预测率最小条目标记预测表的预测结果。若存在相等的情况，再从中选取成功匹配到最长历史信息标记预测表的预测结果；更新阶段不再是直接分配新条目，而需要判断是否再分配新条目的可能性。虽然增强了弱偏差指令的预测准确性，但是在某些应用测试场景其预测准确性可能并不总是优于TAGE，这一发现将在3.3节BATAGE与TAGE分支预测模型对比实验中得到进一步验证。

1.4 现有的预测模型结构

本文指令主要分成条件分支指令和其他类型指令。对于其他类型指令，它们只需要目标预测地址。然而对于条件分支指令，不仅需要提供预测目标地址，而且还需要提供条件分支指令的预测方向。如图7所示，BATAGE分支预测模型负责提供条件分支指令预测方向，BTB（branch target buffer）模块则提供所有指令的目标预测地址，RAS（return address stack）模块专门处理返回指令的目标预测地址。

从图7可知，如果指令是条件分支指令，此时BTB模块与BATAGE分支预测模型会负责提供目标预测地址和目标预测方向。BATAGE分支预测模型将不同长度的分支历史信息与获取的PC值进行哈希运算。然后，在BATAGE分支预测模型的预测机制下，确定条件分支指令的预测方向。另外，获取的PC需要扫描BTB模块的tag表以查找匹配项。若tag表存在匹配项，那么对应targ表的条目提供目标预测地址。如果指令是其他类型指令，那么目标预测地址由BTB和RAS模块提供。对其他类型指令进一步细分，当指令为无条件跳转指令，那么jmp表会提供目标预测地址；当指令为返回指令，那么ret表提供RAS模块的访问地址，RAS模块提供返回指令的目标预测地址。由于现代处理器为超标量处理器，所以获取的PC为一组连续指令，bidx表用于标识一系列连续指令中，哪一条指令负责引发控制流的预测。

BATAGE单一分支预测模型无法完全准确预测各种指令行为，为实现分支预测模型能够在更多的应用测试场景中展现良好的预测效果，一般流行的方案是采用混合预测技术：将两种或者多种分支预测模型结合进行预测，多项预测结果根据某种策略选择最终预测结果。具体解决方案主要分两种：将网络相关预测模型与传统分支预测模型集成［21］，其中网络模型的算法需要大量的训练才能实现最佳性能，这是采用网络模型的弱势之处；将传统主流的分支预测模型进行结合预测，目的在于减少训练时间。本文采用后者方案，鉴于TAGE分支预测模型的高效简单性特点，以及BATAGE分支预测模型能够缓解冷计数器问题的优势，本文提出了一种结合TAGE和BATAGE分支预测模型两者优势的混合预测方法，并且设计相应的混合预测策略来提升分支预测模型在不同应用场景的预测效果。

2 优化的预测模型结构及混合预测策略

2.1 改进的预测模型结构

为解决BATAGE分支预测模型在适应多样化应用测试场景的局限性，本文在现有预测模型结构基础上进行优化，具体如图8所示。与现有预测模型结构相比，不同之处在于增加了TAGE分支预测模型和名为Hybrid的预测模型，Hybrid预测模型本身为一张标记预测表，其条目组成如图9所示，其中tag负责索引匹配，count_tage和count_batage字段分别表示TAGE与BATAGE分支预测模型预测条件分支指令的效用评分。

在优化的预测模型结构中，对于条件分支指令，TAGE和BATAGE分支预测模型会将不同长度分支历史信息和PC进行哈希运算，所得结果在这两种分支预测模型同时进行索引匹配，它们的预测结果转交Hybrid预测模型，Hybrid预测模型会根据混合预测策略选择对应分支预测模型的预测结果。其余方面与原有预测模型结构做法一致。对于其他类型分支指令，与原有的预测模型结构采取相同措施。

在下面的程序段中，一个名为function的函数接收四个整型参数a、b、c、d。该函数主要执行一个条件循环，循环中的加法操作是否执行取决于变量d的状态，这直接影响到程序执行效率。这是因为加法操作的执行依赖于if语句前变量d的值，而循环的持续性则依赖于变量a逐步递减至零。如果这类具有指令依赖性的程序较为少见，可以采用简单的混合预测策略进行处理。相反，如果这类程序较为常见，则需要采取考虑指令依赖性影响的相应混合预测策略。针对指令依赖性问题，已有一些解决方法［22～24］。鉴于此，本文设计了适应性增减策略和权重策略两种混合预测策略，这两种策略将基于TAGE和BATAGE的历史表现来评估并选择最准确的预测结果。具体的指令依赖性示例程序如下：

int function（int a，int b，int c，int d）{

c=a;

a=0;

do{

d=d & 1;

if（d ！=0）{

a=a+c;

}

a=a/2;

c=c * 2;

}while（a ！=0）

}

2.2 适应性增减策略

适应性增减策略以其简单性和直观性为特点，有利于实施和理解，比较适合处理指令依赖性的程序较为少见的情况。在TAGE和BATAGE固有的分支预测模型中，保持简单而有效地选择机制来提高预测准确性，同时降低实施的复杂性。该策略整合了所有的历史信息来评估TAGE和BATAGE分支预测模型的预测能力。

在优化的预测模型结构中，Hybrid预测模型接收来自BATAGE和TAGE分支预测模型的预测结果。Hybrid预测模型需要当前指令PC去匹配预测表的标签。如果没有成功匹配，Hybrid预测模型默认选择TAGE分支预测模型的预测结果。如果匹配成功并且count_tage值比count_batage值大，则TAGE分支预测模型的预测结果具有更加可靠性；否则，采用BATAGE分支预测模型的预测结果。适应性增减策略预测算法的伪代码如算法1所示。

算法1 适应性增减策略预测算法

输入：程序计数器PC和分支历史信息history。

输出：最终预测结果Rfinal。

a）初始化 由PC和history获取TAGE预测结果RTAGE和BATAGE预测结果RBATAGE。

b）将PC和history进行哈希运算得出索引index

c）while t<NUMSIZE do //NUMSIZE为预测表最大条目数

由index找到Hybrid预测模型对应条目hybridEntry;

t←t+1;

end while

d）if hybridEntry.tag≠（PC & 0x3F）then /*若不能成功匹配，PC取低位与标签作匹配*/

Rfinal←RTAGE;

返回Rfinal;

end if

e）if hybridEntry.count_tage<hybridEntry.count_batage then

Rfinal←RBATAGE;

返回Rfinal;

else

Rfinal←RTAGE;

返回Rfinal;

end if

指令执行后需要更新预测模型的条目。TAGE和BATAGE分支预测模型根据各自的算法进行更新。Hybrid预测模型也会更新其预测表的条目：如果最终预测结果与实际执行结果相同，此时会根据预测阶段所选分支预测模型，条目中对应的饱和计数器（count_batage或者count_tage字段）自增。相反，则会发生类似的自减过程。适应性增减策略的更新算法如算法2所示。

算法2 适应性增减策略更新算法

输入：实际执行结果resolveDir，最终预测结果preDir和实际选择分支预测模型tageOrBatage。

输出：更新条目hybridEntry。

a）初始化 根据PC和分支历史信息history使用哈希运算得出索引index

b）while t<NUMSIZE do //NUMSIZE为预测表最大条目数

由index找到Hybrid预测模型对应条目hybridEntry;

t←t+1;

end while

c）if resolveDir=preDir then //若实际结果与预测结果相同

if tageOrBatage=0 then //若此时选择TAGE分支模型

hybridEntry.count_tage自增;

else //若此时选择BATAGE分支模型

hybridEntry.count_batage自增;

end if

else //若实际结果与预测结果不相同

if tageOrBatage=0 then //若此时选择TAGE分支模型

hybridEntry.count_tage自减;

else //若此时选择BATAGE分支模型

hybridEntry.count_batage自减;

end if

end if

返回hybridEntry;

在适应性增减策略中，主要分为预测算法和更新算法。假设Hybrid预测模型的标记预测表最大条目数为N。在预测算法中，步骤a）初始化的时间复杂度为O（1），步骤b）根据哈希运算得到的索引时间复杂度为O（1），步骤c）根据索引查找对应条目的时间复杂度为O（N），步骤d）和e）判断成功或者失败匹配情况的时间复杂度为O（1），经过分析可得到适应性增减策略预测算法的时间复杂度为O（N）；在更新算法中，步骤a）初始化计算的索引时间复杂度为O（1），步骤b）根据索引查找对应条目的时间复杂度为O（N），步骤c）更新条目的时间复杂度为O（1），经过分析可得适应性增减策略更新算法的时间复杂度为O（N）。

2.3 权重策略

权重策略选择最终预测结果基于的前提：最近预测结果比早期预测结果更有价值。对于指令依赖性程序，该策略有助于快速适应最近指令模式行为，并减少早期指令模式行为的影响。适应性增减策略整合了全部历史信息，而权重策略则强调即时性。这种方法特别是在指令模式行为突然转变的情况下，能够提供良好预测能力。

值得注意的是，权重策略采用一次指数平滑法更新Hybrid预测模型的条目。一次指数平滑法是时间序列分析和预测所使用的方法。其核心公式为

St=（1-α）×Yt+α×St-1（2）

其中：St为当前时间的预测值;St-1为上次时间的预测值;Yt是当前时间的实际观测值;α为平滑因子，取值为在0～1。这里采用一次指数平滑法的原因是其计算简单的特点，并且能够减少对硬件资源需求，更加适应中央处理器的高频操作，所以二次和三次指数平滑法不适合用于权重混合预测策略。

指数平滑在时间序列分析中的有效性使得它可以用于分支预测，作为指令模式行为的加权评价方法。在这种情况下，各个变量的含义与原来不同：St表示Hybrid预测模型中标记预测表的饱和计数器更新值；Yt表示Hybrid的预测结果和实际结果的一致性，若Hybrid的预测结果和实际结果一致，则Yt为1，反之为-1；St-1表示Hybrid预测模型中条目的饱和计数器最近一次更新值；α作为衰减因子，调节最近与早期历史信息的影响，衰减因子采用0.01、0.50和0.99，由式（2）可知系数越小越侧重最近指令模式行为。

权重策略预测算法与适应性增减策略是相同的，具体如算法1所示。在权重策略更新算法中，如算法3所示，Hybrid预测模型也会更新其预测表的条目：如果最终预测结果与实际执行结果相同，此时会根据预测阶段所选分支预测模型，条目中对应的饱和计数器（count_batage或者count_tage字段）会基于式（2）进行更新。相反，则会发生类似的更新过程。

算法3 权重策略更新算法

输入：实际执行结果resolveDir，最终预测结果preDir和实际选择分支预测模型tageOrBatage。

输出：更新条目hybridEntry。

a）初始化 根据PC和分支历史信息history使用哈希运算得出索引index

b）while t<NUMSIZE do //NUMSIZE为预测表最大条目数

由index找到Hybrid预测模型对应条目hybridEntry;

t←t+1;

end while

c）if resolveDir=preDir then //若实际结果与预测结果相同

if tageOrBatage=0 then //若此时选择TAGE分支模型

hybridEntry.Count_tage基于式（2）进行更新;

else //若此时选择BATAGE分支模型

hybridEntry.Count_batage基于式（2）进行更新;

end if

else //若实际结果与预测结果不相同

if tageOrBatage=0 then //若此时选择TAGE分支模型

hybridEntry.count_tage基于式（2）进行更新;

else //若此时选择BATAGE分支模型

hybridEntry.count_batage基于式（2）进行更新;

end if

end if

返回hybridEntry;

在权重策略中，主要分为预测算法和更新算法。假设Hybrid预测模型的标记预测表最大条目数为N。在预测算法中，它与适应性增减策略的预测算法相同，所以权重策略预测算法的时间复杂度为O（N）；在更新算法中，步骤a）初始化计算索引的时间复杂度为O（1），步骤b）根据索引查找对应条目的时间复杂度为O（N），步骤c）更新条目的时间复杂度为O（1），经过分析可得权重策略更新算法的时间复杂度为O（N）。

3 仿真实验及结果分析

3.1 分支预测模型参数设置

本文测试对象为TAGE、TAGE-SC-L、BATAGE、multi-perceptron［25］和混合预测模型。预测模型的预测准确性与其配置参数紧密相关。总大小8 Kb量限制并且上下浮动在0.5 Kb以内，确保各种预测模型能够在指定的大小范围进行预测，从而提供更均衡和稳定的预测表现。这种参数配置旨在保持测试的相对公平性。各种预测模型的大小如表1所示。

在TAGE分支预测模型中，基础预测表项数16，每项为2 bit饱和计数器，大小0.003 9 Kb；标记预测表为4张表（每张表项数4 096），其中每项由2 bit置信度、3 bit饱和计数器和11 bit标签组成，大小8 Kb。

在TAGE-SC-L分支预测模型中，TAGE基础预测表项数为128，每项为3 bit饱和计数器，大小为0.046 9 Kb。标记预测表为4张表（每张表项数1 024），每项由2 bit置信度、3 bit饱和计数器和10 bit标签组成，大小7.500 0 Kb。循环预测表（LOOP）项数为8，每项占38 bit，其中记录迭代次数占10 bit，评估置信度占4 bit，记录当前迭代次数占10 bit，标签占10 bit，当前条目的年龄占4 bit，总共大小为0.037 1 Kb。校正器（SC）由存储偏置值的偏置表，记录迭代次数的表，基于分支宽度预测表，基于全局历史表和基于局部历史表组成，每张表项数为128，其中每项为3 bit饱和计数器，大小为0.234 4 Kb。

在multi-perceptron分支预测模型中，其中特征权重大小为1.270 6 Kb，特征权重表以外表所占大小为6.698 7 Kb。

在BATAGE分支预测模型中，基础预测表项数8，每项为3 bit饱和计数器，总计0.002 9 KBit。标记预测表为4张表（每张表项数1 024），其中每项由2个3 bit饱和计数器和10位标签组成，大小8 KBit。

在混合预测模型中，TAGE基础预测表项数为1 024，每项为2 bit饱和计数器，大小0.25 Kb。标记预测表为4张表（每张表项数2 048），每项由2 bit置信度、3 bit饱和计数器和10 bit标签组成，大小3.75 Kb。BATAGE基础预测表项数128，每项为3 bit饱和计数器组成，大小0.046 8 Kb。标记预测表为4张表（每张表项数256），每项由6 bit饱和计数器和10 bit标签组成，大小2 Kb。Hybrid预测模型由1张标记预测表组成，项数1 024，每项由10 bit标签和2个3 bit饱和计数器组成，大小2 Kb。

3.2 仿真平台及数据集

本文采用CBP软件仿真平台进行实验，该平台是分支预测竞赛中使用的分支预测模型性能评估框架，可以测得理想情况下的错误预测率。设计的分支预测模型性能评估框架主要调用预测算法函数和更新算法函数两个不同的函数接口。为了测试分支预测模型的精准度，该过程将每个测试程序转换为指令并且调用预测算法函数进行预测。预测完成之后，调用性能评估框架的更新函数，利用实际执行结果与预测结果是否一致对分支预测模型预测表进行更新。此时一条分支指令已经预测完成，需要预测下一条分支指令，重复此过程。

本文采用的性能指标为MPKI，它表示平均每一千条指令中错误预测分支指令方向的条数。所以，该性能指标越低越好。混合模型在分支预测方面相对于其他主流分支预测模型的性能增强通过式（3）定量表达。

P=MPKI预测模型-MPKI混合模型MPKI预测模型（3）

本文使用CBP软件仿真平台所提供的440个测试程序进行实验，仿真实验数据结果为MPKI。应用场景主要分为LONG_SERVER、LONG_MOBILE、SHORT_SERVER、SHORT_MOBILE四个种类。其中LONG_SERVER测试应用场景有8个测试程序，LONG_MOBILE测试应用场景有32个测试程序，SHORT_SERVER测试应用场景有293个测试程序，SHORT_MOBILE测试应用场景有107个测试程序。在每种测试应用场景中，测试程序最大和最小条件分支指令数情况如表2所示。

本文进行两部分实验：

第一组实验为BATAGE与TAGE验证对比：按照上述440个测试程序划分测试应用场景进行测试，验证BATAGE的MPKI力是否都比TAGE的MPKI值要低。

第二组实验为混合预测模型与最新主流分支预测模型进行横向比较：TAGE、TAGE-SC-L、BATAGE、multi-perceptron与混合模型进行对比实验，将混合分支预测模型得到的总体MPKI和各种测试应用场景的总体MPKI与这些主流分支预测模型进行比较。

3.3 BATAGE与TAGE验证对比

在验证对比实验中，在总体MPKI方面上，BATAGE比TAGE性能优于7.833%，BATAGE与TAGE分支预测模型的总体MPKI如表3所示。

图10可知，在四类测试应用场景中：LONG_MOBILE与SHORT_MOBILE的测试结果反映为TAGE的总体MPKI比BATAGE低。其中在LONG_MOBILE测试集种类中，TAGE的总体MPKI为2.779，BATAGE的总体MPKI为3.549；在SHORT_MOBILE测试集种类中，TAGE的MPKI为3.614，BATAGE的MPKI为3.804。所以上述结果表明：在有些测试应用场景中，BATAGE的预测能力不如TAGE。此时需要采用混合预测方式来提升预测精度，对于总体MPKI与各种测试应用场景的总体MPKI，在3.4节将会进一步详细展示。

3.4 仿真结果分析

本节在BATAGE不能适应所有测试应用场景的基础上，进一步横向比较混合模型与最新主流分支预测模型。在仿真结果上，展示混合模型与各个分支预测模型的总体MPKI与各个应用测试应用场景下的MPKI值，以及测试最佳MPKI与最差MPKI，性能结果提升由式（3）得出。具体各种预测模型的MPKI值如表4所示。根据结果可知，混合模型（权重策略，α=0.01）的MPKI为5.961，其值低于各个最新主流分支预测模型的MPKI。与较优秀的TAGE-SC-L分支预测模型相比，混合模型（权重策略，α=0.01）预测准确性提升3.06%。

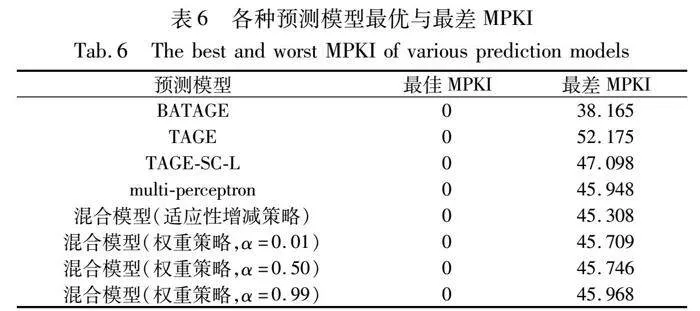
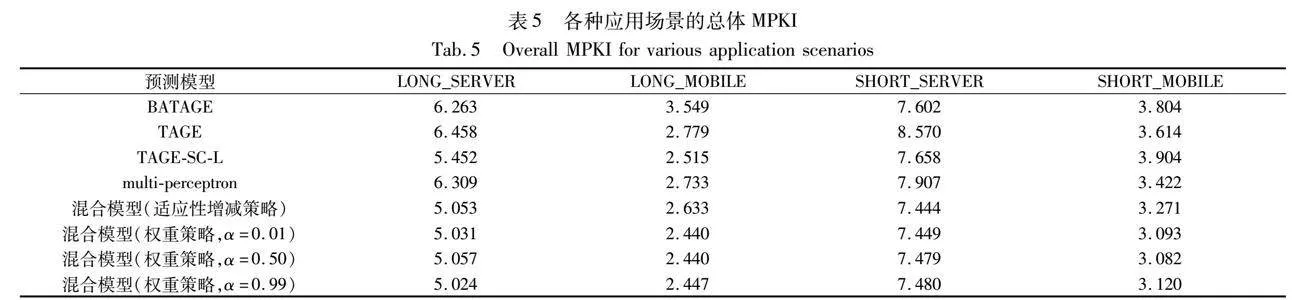
从表5、6可知：在LONG_SERVER测试应用场景中，混合模型（权重策略，α=0.99）表现最佳，其MPKI为5.024，相较于表现最佳的TAGE-SC-L分支预测模型提升了7.85%；在LONG_MOBILE测试应用场景中，混合模型（权重策略，α=0.50，0.01）表现最佳，相较于表现最佳的multi-perceptron分支预测模型提升仅为2.98%；在SHORT_SERVER测试应用场景中，混合模型（适应性增减策略）表现最佳，其MPKI为7.444，相较于表现最佳的BATAGE分支预测模型提升了2.08%；在SHORT_MOBILE测试应用场景中，混合模型（权重策略，α=0.50）表现最佳，其MPKI为3.082，相较于表现最佳的multi-perceptron分支预测模型提升了9.94%。在最佳MPKI与最差MPKI的情况中：各种预测模型的最佳MPKI都一样；各种预测模型的最差MPKI，表现最佳的BATAGE分支预测模型比混合预测模型具有更为稳健的预测能力。

从仿真实验结果可知：观察总体MPKI和各种测试应用场景的总体MPKI，混合预测模型的预测能力优于最新主流的分支预测模型。这一改进归因于混合预测模型能够融合两种分支预测模型的优势，有效利用它们在不同测试应用场景的优势，从考虑指令依赖性角度设计两种不同的混合预测策略来提高条件分支指令预测的准确性。

4 结束语

在分支预测中，往往存在分支预测模型不能准确预测某种应用场景的问题。针对该情况，本文提出两种不同的混合预测策略方案来缓解该问题。将BATAGE与TAGE分支预测模型的预测结果转交Hybrid预测模型，Hybrid通过混合预测策略得出最终预测结果。本文首先验证BATAGE的总体MPKI力是否都比TAGE的总体MPKI值要低，然后对混合模型与最新主流分支预测模型从总体MPKI、各种测试应用场景的总体MPKI、最佳与最差MPKI三个方面进行横向比较。本文实验结果表明：除了最佳MPKI和最差MPKI方面，混合预测模型表现比各种主流分支预测模型要好。未来将利用神经网络相关模型的优越学习能力，在尽量不增大训练时间的情况下，将BATAGE预测模型与神经网络模型相结合来提升预测准确度。

参考文献：

［1］Smith J E，Sohi G S.The microarchitecture of superscalar processors［J］.Proceedings of the IEEE，1995，83（12）：1609-1624.

［2］Healy I，Giordano P，Elmannai W.Branch prediction in CPU pipeli-ning［C］//Proc of the 14th Annual Ubiquitous Computing，Electronics & Mobile Communication Conference.Piscataway，NJ：IEEE Press，2023：364-368.

［3］Mittal S.A survey of techniques for dynamic branch prediction［J］.Concurrency and Computation：Practice and Experience，2019，31（1）：e4666.

［4］Smith J E.A study of branch prediction strategies［C］//Proc of the 8th Annual Symposium on Computer Architecture.1981：135-148.

［5］McFarling S.Combining branch predictors，Technical Report TN-36［R］.［S.l.］：Digital Western Research Laboratory，1993.

［6］Seznec A，Michaud P.A case for（partially）TAGGED GE-OMETRIC history length branch prediction［J］.The Journal of Instruction-Level Parallelism，2006，8：23.

［7］Seznec A.TAGE-SC-L branch predictors again［C］//Proc of the 5th JILP Workshop on Computer Architecture Competitions：Championship Branch Prediction.2016.

［8］Seznec A.A 256 kbits L-TAGE branch predictor［J］.Journal of Instruction-Level Parallelism Special Issue：The Second Championship Branch Prediction Competition，2007，9：1-6.

［9］Seznec A.A 64 Kbytes ISL-TAGE branch predictor［C］//Proc of the 2nd JILP Workshop on Computer Architecture Competitions：Championship Branch Prediction.2011.

［10］李正平，高杨.一种改进型TAGE分支预测器的实现［J］.辽宁工业大学学报：自然科学版，2020，40（1）：1-4.（Li Zhengping，Gao Yang.Implementation of improved TAGE branch predictor［J］.Journal of Liaoning University of Technology：Natural Science Edition，2020，40（1）：1-4.）

［11］Villon L A Q，Susskind Z，Bacellar A T L，et al.A conditional branch predictor based on weightless neural networks［J］.Neurocomputing，2023，555：126637.

［12］Zhao J，Korpan B，Gonzalez A，et al.SonicBoom：the 3rd generation Berkeley out-of-order machine［C］//Proc of the 4th Workshop on Computer Architecture Research with RISC-V.2020：1-7.

［13］Zhao J，Gonzalez A，Amid A，et al.CODRA：a framework for evaluating compositions of hardware branch predictors［C］//Proc of the 22nd IEEE International Symposium on Performance Analysis of Systems and Software.Piscataway，NJ：IEEE Press，2021：310-320.

［14］Suggs D，Subramony M，Bouvier D.The AMD “zen 2” processor［J］.IEEE Micro，2020，40（2）：45-52.

［15］Evers M，Barnes L，Clark M.The AMD next-generation“zen 3”core［J］.IEEE Micro，2022，42（3）：7-12.

［16］Jiménez D A，Lin C.Dynamic branch prediction with perceptrons［C］//Proc of the 7th HPCA International Symposium on High-Performance Computer Architecture.Piscataway，NJ：IEEE Press，2001：197-206.

［17］Zangeneh S，Pruett S，Lym S，et al.BranchNet：a convolutional neural network to predict hard-to-predict branches［C］//Proc of the 53rd Annual IEEE/ACM International Symposium on Microarchitecture.Piscataway，NJ：IEEE Press，2020：118-130.

［18］Al-Khalid A S，Omran S S.Hybrid branch prediction for pipelined MIPS processor［J］.Journal of Electrical and Computer Engine-ering，2020，10（4）：3476.

［19］Dang N M，Cao Haixuan，Tran L.BATAGE-BFNP：a high-performance hybrid branch predictor with data-dependent branches speculative pre-execution for RISC-V processors［J］.Arabian Journal for Science and Engineering，2023，48（8）：10299-10312.

［20］Michaud P.An alternative TAGE-like conditional branch predictor［J］.ACM Trans on Architecture and Code Optimization，2018，15（3）：1-23.

［21］陈智勇，廉海涛，吴星星.一种改进的神经网络分支预测技术［J］.微电子学与计算机，2014，31（11）：152-155.（Chen Zhiyong，Lian Haitao，Wu Xingxing.An improved branch prediction based on the neural network［J］.Microelectronics & Computer，2014，31（11）：152-155.）

［22］Pruett S，Patt Y.Branch runahead：an alternative to branch prediction for impossible to predict branches［C］//Proc of the 54th Annual IEEE/ACM International Symposium on Microarchitecture.2021：804-815.

［23］Khan T A，Ugur M，Nathella K，et al.Whisper：profile-guided branch misprediction elimination for data center applications［C］//Proc of the 55th IEEE/ACM International Symposium on Microarchitecture.Piscataway，NJ：IEEE Press，2022：19-34.

［24］Villon P S M.Maintaining high performance in the presence of impossible-to-predict branches［D］.Austin：The University of Texas at Austin，2022.

［25］Jiménez D A.Multiperspective perceptron predictor［C］//Proc of the 5th JILP Workshop on Computer Architecture Competitions：Championship Branch Prediction.2016.

收稿日期：2023-12-25

修回日期：2024-03-18

基金项目：国家重点研发计划资助项目（2021YFF0601200，2021YFF0601204）

作者简介：方昕宇（1996—），男，湖北黄冈人，硕士，CCF会员，主要研究方向为计算机体系结构；周日贵（1973—），男（通信作者），江西南昌人，教授，博导，博士，主要研究方向为智能信息处理、智能信息相关软硬件系统的开发（rgzhou@shmtu.edu.cn）；龚鸣清（1994—），男，湖北黄冈人，硕士，主要研究方向为高性能计算.