抗恶意敌手的线性门限隐私集合交集协议

摘 要：门限隐私集合交集（TPSI）是安全多方计算中的一种特例，其在机器学习、共享拼车、指纹识别等多个领域有广泛的应用。然而，目前存在的方案均基于计算复杂度较高的算法，并且仅在半诚实模型下实现，导致协议计算开销较大且无法抵抗恶意敌手的攻击。为了解决以上问题，首先提出了一个向量不经意匹配测试（VOMT）协议，并基于VOMT和布谷鸟哈希设计了一个高效的半诚实TPSI协议。此外，结合VOMT与对称密钥加密方案构造出向量不经意解密匹配测试（VODMT）协议，并基于VODMT与不经意伪随机函数设计了一个可以抵抗恶意敌手的TPSI协议。随后，分别在半诚实模型和恶意模型下证明了协议的安全性，并分析得出两个协议的计算复杂度和通信复杂度均为线性。在集合大小为4 096时，提出的两个协议的在线运行时间分别为0.81 s和1.81 s，而先前的工作则需要5 627 s，所以两个协议均是高效的。

关键词：隐私计算； 门限隐私集合交集； 不经意键值对存储； 不经意伪随机函数； 布谷鸟哈希

中图分类号：TP309 文献标志码：A

文章编号：1001-3695（2024）09-039-2846-08

doi：10.19734/j.issn.1001-3695.2023.12.0601

Linear threshold private set intersection against malicious adversaries

Jia Zhengkuna， Zhang Ena，b， Wang Mengtaoa

（a.School of Computer & Information Engineering， b.Key Laboratory of Artificial Intelligence & Personalized Learning in Education of Henan Province， Henan Normal University， Xinxiang Henan 453007， China）

Abstract：Threshold private set intersection（TPSI） is a special case of secure multi-party computation， which is widely used in many fields such as machine learning， ride-sharing， and fingerprint recognition. However， currently existing solutions are all based on algorithms with high computational complexity and are only implemented under a semi-honest model， resulting in high computational overhead and inability to resist attacks by malicious adversaries. In order to solve the above problems， this paper first proposed a vector oblivious match test（VOMT） protocol and designed an efficient semi-honest TPSI protocol based on VOMT and cuckoo hashing. In addition， it combined VOMT and symmetric key encryption schemes to construct the vector oblivious decryption matching test（VODMT） protocol and designed a TPSI protocol based on VODMT and oblivious pseudo-random functions that could resist malicious adversaries. Subsequently， it proved the security of the protocol under the semi-honest model and the malicious model respectively， and analyzed that the computational complexity and communication complexity of the two protocols were linear. When the set size is 4 096， the online running time of the two proposed protocols is 0.81 s and 1.81 s respectively， while the previous work required 5 627 s， so both protocols are efficient.

Key words：private compute; threshold private set intersection; oblivious key-value stores; oblivious pseudorandom function; cuckoo hash

0 引言

在隐私集合交集（private set intersection，PSI）协议中，两个互不信任的参与方P0和P1分别输入自己的集合X0和X1，最终在不泄露任何额外信息的情况下让参与方得到两个集合的交集X0∩X1。在过去十年中，PSI协议在两方恶意［1］、多方恶意［2］、云辅助模型［3］、小数据集模型［4］和抗量子领域［5］等方向的研究都取得了极大进展，并在文献［6］中进行了详细的总结。此外，PSI作为一种隐私保护技术在许多场景中得到了应用，如多源异构数据融合［7］、新冠接触者行程［8］、广告曝光度计算［9］和机器学习［10］等。

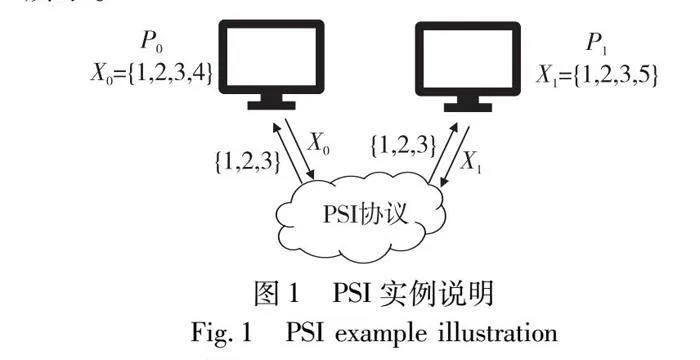
然而，在一些特殊场景下只有当交集足够大时，参与方才有得到交集的动机。例如在隐私保护共享乘车应用［11］中，只有当乘客大部分行程相同时才会选择拼车。所以门限隐私集合交集（threshold private set intersection，TPSI）协议是PSI问题的一个特例，即当且仅当两个参与者P0和P1的集合的交集基数|X0∩X1|达到门限值t时，参与方才能得到交集X0∩X1的信息，否则协议中止，参与方得不到关于交集的任何信息，如图1和2所示。

Freedman等人［12］首次提出了TPSI协议的概念，并在半诚实模型下设计了一个基于平衡哈希和同态加密的安全门限值测试协议，并基于此协议来实现了TPSI协议。Zhao等人［13］提出了一种基于秘密共享和半同态加密技术的门限秘密传输方案来实现两方TPSI协议，但是该协议会泄露交集基数。Ghosh等人［14］提出了一种评估随机线性函数的工具，并构建了一个基于弹性秘密共享 （robust secret sharing，RSS）和代数技术的两方TPSI协议。然而，代数技术需要大量的插值运算，导致协议的通信开销较大。此外，RSS 解码（即Reed-Solomon码）算法的计算复杂度为O（n3），使得该协议无法在大集合上运行。

Hallgren等人［11］在半诚实模型下设计了一种两方TPSI协议，并将其用于具有隐私保护的共享拼车应用中，这使乘客能够在不泄露旅行行程的情况下进行拼车。但是该协议具有O（n3）的计算复杂度和O（n2）的通信复杂度。Zhao等人［15］基于加法同态加密和不经意多项式计算在半诚实模型下构建了两种两方TPSI协议，分别在交集基数大于和小于门限值时输出交集。Ghosh等人［16］研究了TPSI协议的通信复杂度，指出通信的下界为O（t），其中t为集差。此外，他们设计了一个基于加法同态加密的TPSI协议，将协议的通信复杂度降低到O（t2）。但是，当集差t较大时，协议的通信复杂度较大，即O（t2）≈O（n2）。

Rindal等人［17］提出了一种基于向量不经意线性评估（vector oblivious linear evolution，Vole）的不经意伪随机函数（oblivious pseudo-random function，OPRF） ，并用它实现了电路PSI协议，但该协议不能抵抗恶意敌手。Ghosh等人［18］设计了一个基于加性同态加密、不经意传输和通用安全计算的拟线性复杂度的两方TPSI协议，但是该协议处于理论阶段并未具体实现。Raghuraman等人［19］提出了一种新的不经意键值对存储（obli-vious key-value stores，OKVS）的构造方式，提高了OKVS方案的编解码效率，并将其应用在文献［18］的电路PSI协议中，进一步减少了协议的计算开销，但不能抵抗恶意敌手。

张恩等人［20］提出了一个基于弹性秘密共享的多方TPSI协议。协议分为轻量级协议和增强协议，分别可以抵抗不同程度的敌手合谋。但是该协议在秘密共享重构阶段同样使用了RSS算法，在重构阶段的计算复杂度为O（n3），所以协议无法在大集合下运行。此外，魏立斐等人［21］提出了一种双云辅助的超阈值多方隐私集合交集（over-threshold multi-party private set intersection，OT-MP-PSI）协议，参与方共同计算至少属于t个参与方集合交集的元素。该协议将计算复杂度较高的秘密分发和秘密重构过程分别交给两个不可信的云服务器来完成，可以解决参与者计算能力较弱和计算能力不平衡的问题。但是该OT-MP-PSI协议在秘密重构过程需要由服务器重遍历整个有限域，所以协议的计算开销较大。Liu等人［22］首次提出了概率TPSI协议的概念，各参与方有与交集大小相关的概率获得交集，并将Goldwasser-Sipser证明系统扩展至多方设置，实现多方概率交集基数测试协议。该协议可以绕过计算交集基数的通信下界，极大地减少了协议的开销。

综上，现存的TPSI协议均在半诚实模型下实现，并且使用了同态加密、RSS和多项式插值等计算复杂度较高的算法。在用户数据较大的场景下，采用以上算法的协议需要较长的运行时间，交集信息无法及时反馈给用户。此外这些协议，无法抵抗恶意敌手的攻击。本文提出了两种TPSI协议，分别可以在半诚实模型和恶意模型下运行，并且两个协议避免了计算成本较高的算法，仅需要使用对称密钥算法和计算复杂度为O（n）的通用两方安全计算。本文的主要贡献如下：

a）在半诚实模型下设计了一个高效的两方TPSI协议，该协议基于哈希技术、OKVS和向量不经意匹配测试（vector oblivious match test，VOMT）算法。通过哈希技术和OKVS减少了协议在安全门限值测试阶段的计算复杂度。此外，使用VOMT算法提高了协议的计算效率，使协议在集合较大时仍可以高效运行。

b）由于哈希技术无法在恶意模型下使用［23］，本文提出了向量不经意解密匹配测试（vector oblivious decoding matching test，VODMT）算法，使用VODMT、OPRF和对称密钥加密方案减少了协议在安全门限值测试阶段的计算复杂度，从而构造出了第一个可以在恶意模型下运行的两方TPSI协议。

c）分析并得出本文提出的两个TPSI协议的计算复杂度和通信复杂度均为线性，并分别在恶意模型和半诚实模型下证明了协议的安全性。

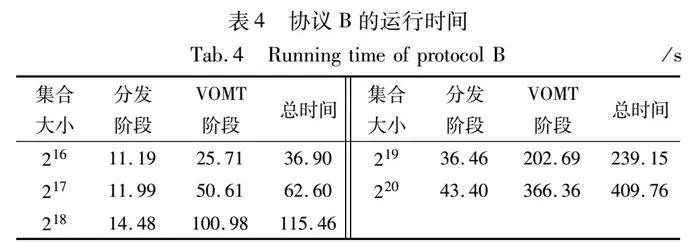
d）在不同大小集合下测试了协议的运行时间。当集合大小为220时，协议的在线运行时间分别为226.20 s和409.76 s，是第一个可以在大集合（220）下运行的TPSI协议，并通过实验对比得出本文的协议优于先前的工作。

1 基础知识

1.1 安全模型

安全模型包括半诚实安全模型和恶意安全模型。在半诚实安全模型下，敌手严格按照协议要求执行，但是会试图在交互过程中获取额外信息。而在恶意模型下，敌手可以任意偏离协议，通过修改或省略消息等手段来获取额外信息。本文中的协议均为两方协议，在安全证明中只考虑其中一方腐败的情形，且本文中对安全模型和腐败参与方的定义遵循文献［24，25］中的定义。

在半诚实模型中，设π是理想两方协议，用M表示任意参与方子集。在M中参与方在执行输入为（x，y）的协议π时，其视图表示为viewπM（x，y，e）=（，rM1，…，rMt，m），其中e为安全参数，表示M中各个参与方的输入，rM1，…，rMt表示在执行过程中产生的随机值，m表示在执行协议过程中收到的消息。

定义1 令f为一个确定性函数。如果存在一个概率多项式时间算法S，满足：

4 性能分析

在下文中分别使用协议A和B来表示本文2.1节和3.1节中所提出的协议。

4.1 计算复杂度分析

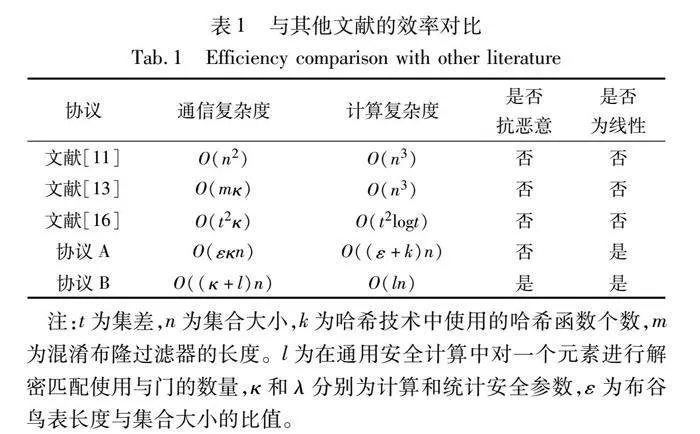
本节对协议的计算复杂度进行分析。对于协议A，在哈希技术阶段的计算复杂度与使用的哈希函数的数量有关，为O（kn）。在OKVS编码和解码算法阶段的计算复杂度分别为O（εn+λ）和O（εn），在VOMT阶段的计算复杂度为O（εn）。由此可见，协议A的计算复杂度为O（（ε+k）n）。对于协议B，在OPRF阶段和OKVS编解阶段协议的计算复杂度均为O（n），而在VODMT阶段协议的计算复杂度为O（ln），l为在通用安全计算中对一个元素进行解密匹配所使用与门的数量。因此，协议B的计算复杂度为O（ln）。

4.2 通信复杂度分析

本节对协议的通信复杂度进行分析。对于协议A，在发送数据结构D阶段的通信复杂度为O（εnλ），在进行VOMT阶段的通信复杂度为O（εnλ）。所以协议A的通信复杂度为O（εnλ）。对于协议B，在OPRF阶段和发送数据结构D阶段的通信复杂度均为O（n），在VODMT阶段的通信复杂度为O（（κ+l）n）。所以协议B的通信复杂度为O（（κ+l）n）。

4.3 复杂度对比

本节分别对比了本文协议与之前工作的计算复杂度与通信复杂度，如表1所示。

4.4 实验和对比

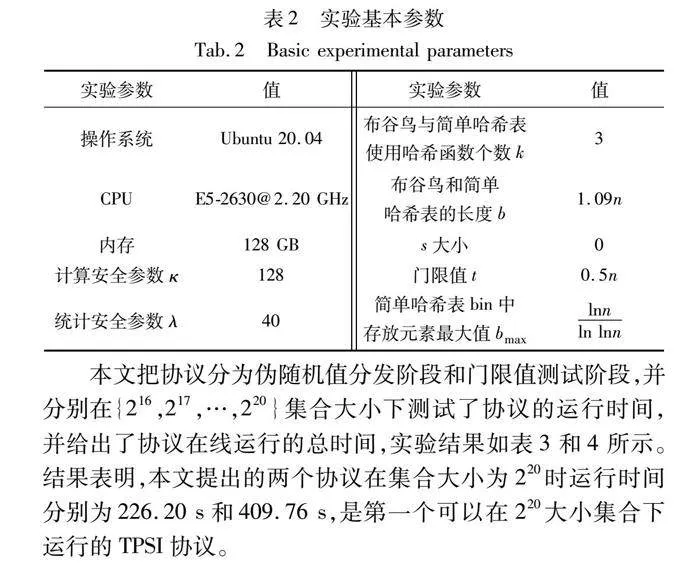
本文的协议使用Java和部分C++实现，VOMT功能使用ABY协议实现。VODMT功能使用SPDZ协议（https：//github.com/data61/MP-SPDZ）和mpc4j库（https：//github.com/ali-baba-edu/mpc4j）实现。本文使用的OKVS方案和OPRF方案通过文献［20］中的代码实现。实验中的其他参数及取值如表2所示，其中n表示集合大小。

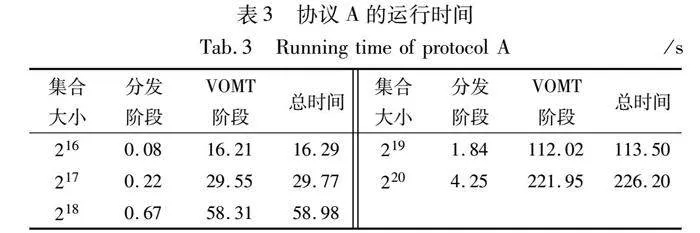
本文把协议分为伪随机值分发阶段和门限值测试阶段，并分别在{216，217，…，220}集合大小下测试了协议的运行时间，并给出了协议在线运行的总时间，实验结果如表3和4所示。结果表明，本文提出的两个协议在集合大小为220时运行时间分别为226.20 s和409.76 s，是第一个可以在220大小集合下运行的TPSI协议。

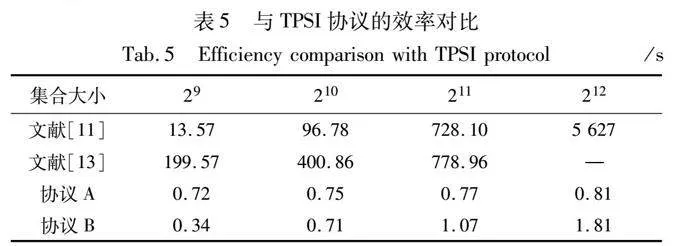
本文与现存的TPSI协议在不同集合大小下对比了协议的nzCbdxYKkLqWAN4V2tkNSA==运行时间，由于暂时无法找到可以抵抗恶意敌手的TPSI协议，所以本文与目前可实现的半诚实两方TPSI协议进行对比，对比结果如表5所示。

根据表5可以看出，协议A和B在211大小的集合下的运行时间分别为0.77 s和1.07 s，而文献［11，13］的协议则需要728.10 s和778.96 s，所以本文协议在运行效率上相较于以往工作有较大提升。

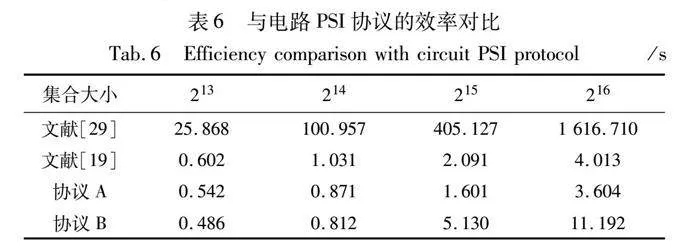
电路PSI协议理论上可以在交集上实现任何功能，但现存的电路PSI协议暂未实现门限值测试功能，所以本文在与电路PSI协议对比时减去了门限值测试阶段所消耗的时间（即标准两方PSI协议），对比结果如表6所示。

从表6中可以看出，协议A和B相较于文献［29］在运行时间上均有较大提升。协议A相较于文献［19］在运行时间上提升了约10%，而协议B在集合大小小于215时协议的运行时间优于文献［19］，并且文献［19，29］均无法抵抗恶意敌手，所以本文协议在不同的模型下都具有较好的实用性。

5 结束语

本文提出了可以抵抗半诚实敌手和恶意敌手的两方TPSI协议，根据实验数据表明本文的协议可以在大数据集下高效运行，具有较好的实用价值。此外，可以从实验中得出，虽然协议效率有一定提升，但是安全门限值测试阶段仍然占协议开销的较大部分，因此之后将研究设计一个更高效的安全门限值测试协议和实现多方恶意门限隐私集合交集协议。

参考文献：

［1］Pinkas B， Rosulek M， Trieu N， et al. PSI from PaXoS： fast， malicious private set intersection［C］//Proc of Annual International Conference on Theory and Applications of Cryptographic Techniques. Cham： Springer， 2020： 739-767.

［2］Zhang En， Liu Fenghao， Lai Qiqi， et al. Efficient multi-party private set intersection against malicious adversaries［C］//Proc of ACM SIGSAC Conference on Cloud Computing Security Workshop. New York：ACM Press， 2019： 93-104.

［3］张静， 田贺， 熊坤， 等. 基于云服务器的公平多方隐私集合交集协议［J］. 计算机应用， 2023，43（9）：2806-2811. （Zhang Jing， Tian He， Xiong Kun， et al. Fair multi-party private set intersection protocol based on cloud server［J］. Journal of Computer Applications， 2023，43（9）：2806-2811.）

［4］张蕾， 贺崇德， 魏立斐. 高效且恶意安全的三方小集合隐私交集计算协议［J］. 计算机研究与发展， 2022， 59（10）： 2286-2298. （Zhang Lei， He Chongde， Wei Lifei. Efficient and malicious secure three-party private intersection computation protocol for small set［J］. Computer Research and Development， 2022， 59（10）： 2286-2298.）

［5］赵宗渠， 王书静， 汤永利， 等. 基于理想格的两方隐私集合交集协议［J］. 计算机应用研究， 2023， 40（12）： 3795-3799. （Zhao Zongqu， Wang Shujing， Tang Yongli， et al. Two-party privacy set intersection protocol based on ideal lattice［J］. Application Research of Computers， 2023， 40（12）： 3795-3799.）

［6］魏立斐， 刘纪海， 张蕾. 面向隐私保护的集合交集计算综述［J］. 计算机研究与发展， 2022， 59（8）： 1782-1799. （Wei Lifei， Liu Jihai， Zhang Lei. Survey of privacy preserving oriented set intersection computation［J］. Computer Research and Development， 2022， 59（8）： 1782-1799.）

［7］丁江， 张国艳， 魏子重，等. 面向多源异构数据融合的隐私集合求交研究［J］. 信息网络安全， 2023， 23（8）： 86-98. （Ding Jiang， Zhang Guoyan， Wei Zichong， et al. Multi-source heteroge-neous data collaboration via private set intersection［J］. Netinfo Secu-rity， 2023， 23（08）： 86-98.）

［8］Duong T， Phan D H， Trieu N. Catalic： delegated PSI cardinality with applications to contact tracing［C］//Proc of the 26th Internatio-nal Conference on Theory and Application of Cryptology and Information Security. Cham：Springer， 2020： 870-899.

［9］Lyu Siyi， Ye Jinhui， Yin Sijie， et al. Unbalanced private set intersection cardinality protocol with low communication cost［J］. Future Generation Computer Systems， 2020， 102： 1054-1061.

［10］Mohassel P， Zhang Yupeng. SecureML： a system for scalable privacy-preserving machine learning［C］//Proc of IEEE Symposium on Secu-rity and Privacy. Piscataway，NJ：IEEE Press， 2017： 19-38.

［11］Hallgren P， Orlandi C， Sabelfeld A. PrivatePool： privacy-preserving ridesharing［C］//Proc of the 30th IEEE Computer Security Foundations Symposium. Piscataway，NJ：IEEE Press， 2017： 276-291.

［12］Freedman M J， Nissim K， Pinkas B. Efficient private matching and set intersection［C］//Proc of International Conference on Theory and Applications of Cryptographic Techniques. Berlin： Springer， 2004： 1-19.

［13］Zhao Yongjun， Chow S S M. Are you the one to share？Secret transfer with access structure［EB/OL］. （2015）. https：//eprint.iacr.org/2015/929.

［14］Ghosh S， Nilges T. An algebraic approach to maliciously secure private set intersection［C］//Proc of Annual International Conference on Theory and Applications of Cryptographic Techniques. Cham： Sprin-ger， 2019： 154-185.

［15］Zhao Yongjun， Chow S S M. Can you find the one for me？［C］//Proc of Workshop on Privacy in Electronic Society. New York： ACM Press，2018： 54-65.

［16］Ghosh S， Simkin M. The communication complexity of threshold private set intersection［C］//Proc of Annual International Cryptology Conference. Cham： Sprin-ger， 2019： 3-29.

［17］Rindal P， Schoppmann P. VOLE-PSI： fast OPRF and circuit-PSI from vector-OLE［C］//Proc of Annual International Conference on Theory and Applications of Cryptographic Techniques. Cham： Springer International Publishing， 2021： 901-930.

［18］Ghosh S， Simkin M. Threshold private set intersection with better communication complexity［C］//Proc of International Conference on Public-Key Cryptography. Cham： Springer， 2023： 251-272.

［19］Raghuraman S， Rindal P. Blazing fast PSI from improved OKVS and subfield VOLE［C］//Proc of ACM SIGSAC Conference on Computer and Communications Security. New York： ACM Press， 2022： 2505-2517.

［20］张恩， 秦磊勇， 杨刃林， 等. 基于弹性秘密共享的多方门限隐私集合交集协议［J］. 软件学报， 2023，34（11）：5424-5441. （Zhang En， Qin Leiyong， Yang Renlin， et al. Multi-party threshold private set intersection protocol based on robust secret sharing［J］. Journal of Software， 2023，34（11）：5424-5441.）

［21］魏立斐， 刘纪海， 张蕾， 等. 双云辅助的超阈值多方隐私集合交集计算协议［J］. 软件学报， 2023，34（11）：5442-5456. （Wei Lifei， Liu Jihai， Zhang Lei， et al. Two cloud-assisted over-threshold multi-party private set intersection calculation protocol［J］. Journal of Software， 2023，34（11）：5442-5456.）

［22］Liu Fenghao， Zhang En， Qin Leiyong. Efficient multiparty probabilistic threshold private set intersection［C］//Proc of ACM SIGSAC Conference on Computer and Communications Security. New York：ACM Press， 2023： 2188-2201.

［23］Rindal P， Rosulek M. Malicious-secure private set intersection via dual execution［C］//Proc of ACM SIGSAC Conference on Computer and Communications Security. New York：ACM Press， 2017： 1229-1242.

［24］Lindell Y. How to simulate it—a tutorial on the simulation proof technique［M］//Tutorials on the Foundations of Cryptography： Dedicated to Oded Goldreich. 2017： 277-346.

［25］Rindal P， Rosulek M. Improved private set intersection against malicious adversaries［C］//Proc of Annual International Conference on Theory and Applications of Cryptographic Techniques. Cham： Sprin-ger International Publishing， 2017： 235-259.

［26］Gonnet G H. Expected length of the longest probe sequence in hash code searching［J］. Journal of the ACM， 1981， 28（2）： 289-304.

［27］Pagh R， Rodler F F. Cuckoo hashing［J］. Journal of Algorithms， 2004， 51（2）： 122-144.

［28］Pinkas B， Schneider T， Zohner M. Scalable private set intersection based on OT extension［J］. ACM Trans on Privacy and Security， 2018， 21（2）： 1-35.

［29］Pinkas B， Schneider T， Tkachenko O， et al. Efficient circuit-based PSI with linear communication［C］//Proc of the 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques. Cham：Springer， 2019： 122-153.

收稿日期：2023-12-11；修回日期：2024-01-26 基金项目：国家自然科学基金资助项目（62072159，62002103，6207608）；河南省科技攻关项目（232102211057）

作者简介：贾正坤（1999—），男，河南新乡人，硕士研究生，主要研究方向为安全多方计算；张恩（1974—），男（通信作者），河南新乡人，教授，硕导，博士，主要研究方向为安全多方计算（zhangenzdrj@163.com）；王梦涛，男，河南周口人，硕士研究生，主要研究方向为安全多方计算．