一种基于共轭次梯度算法的非光滑布图规划方法

摘 要：针对只有硬模块的布图规划问题，通常将其构建成组合优化模型，但求解过程时间成本高。为提高求解效率，提出了一种基于非光滑解析数学规划的布图规划算法。基于布图中器件的坐标表示，构建了一个泛化的非光滑解析数学规划模型，将不同场景下的布图规划问题的不同优化阶段处理为该泛化模型的特例，并利用共轭次梯度算法（conjugate sub-gradient algorithm，CSA）对其进行求解。针对固定轮廓布图规划问题，通过统一框架下的全局布图规划、合法化、局部优化三个阶段，实现了在固定轮廓约束下的线长优化。针对无固定轮廓约束问题，提出了带黄金分割策略的共轭次梯度算法（conjugate sub-gradient algorithm with golden section strategy，CSA_GSS），利用黄金分割策略缩小固定轮廓的面积，达到面积和线长双优化的效果。实验在GSRC测试电路上与基于B*-树表示的布图规划算法进行比较，该算法对于大规模电路在线长和时间方面均占据优势。实验结果表明，该算法能以更低的时间复杂度获得更优的线长。

关键词：大规模集成电路；布图规划；非光滑优化；固定轮廓；共轭次梯度法

中图分类号：TP391 文献标志码：A 文章编号：1001-3695（2024）09-026-2751-07

doi：10.19734/j.issn.1001-3695.2023.12.0628

Non-smooth floorplanning method based on conjugate sub-gradient algorithm

Sun Jian1a，Xu Ning1b，Wu Jian1b，Zhu Zhanyang1b，Chen Yu1a，Hu Jianguo2

（1.a.School of Science，b.School of Information Engineering，Wuhan University of Technology，Wuhan 430070，China;2.Shenzhen Research Institute，Sun Yat-Sen University，Shenzhen Guangdong 528406，China）

Abstract：Aiming at the floorplanning problem with only hard modules，it is usually constructed as a combinatorial optimization model，but the time cost of solving process is high.In order to improve the solving efficiency，this paper proposed a floorplanning algorithm based on non-smooth analytic mathematical programming.Based on the coordinate representation of mo-dules，this paper established a non-smooth mathematical programming model，which was a generalization of the optimization models corresponding to various optimization stages of different cases that were solved by the conjugate sub-gradient algorithm（CSA）.Aiming at the fixed-outline floorplanning problem，this paper achieved wirelength optimization under fixed-outline constraint through the general framework consisted of three stages：global floorplanning，legalization and local optimization.To address the case without fixed-outline constraint，this paper proposed a conjugate sub-gradient algorithm with golden section stra-tegy（CSA_GSS）.The algorithm adopted golden section strategy to reduce the area of the fixed-outline and to achieve the dual effect of both area and wirelength optimization.Compared with floorplanning algorithm based on B*-tree on GSRC test circuit，the proposed algorithm had advantages in terms of wirelength and time for large-scale circuits.Experimental results show that the algorithm can obtain better wirelength with lower time complexity.

Key words：VLSI;floorplanning;non-smooth optimization;fixed-outline;conjugate sub-gradient algorithm

0 引言

布图规划是超大规模集成电路（very large-scale integration circuit，VLSI）物理设计中的重要步骤，布图结果对VLSI芯片的性能具有重要影响［1］。然而，VLSI布图规划需要在满足约束条件的情况下考虑线长、面积等多个优化目标来实现模块的最佳放置，是一个具有复杂约束的多目标优化问题［2］。随着集成电路技术的发展，VLSI布图规划场景越来越复杂，为高性能布图规划算法的设计带来巨大的挑战。

根据所建立的布图规划数学规划模型，可将布图规划算法分为基于组合优化模型的布图规划算法（floorplanning algorithm based on a combinatorial optimization model，FA-COM）和基于解析优化模型的布图规划算法（floorplanning algorithm based on an analytical optimization model，FA-AOM）两类。采用特定的布图编码刻画布图模块之间的相对位置关系，FA-COM利用启发式算法或元启发式算法来求解布图规划的大规模组合优化模型，进而得到优化的布图结果［3～6］；虽然对相对位置关系的解码结果能够自然地满足模块的互不重叠约束，但算法的收敛速度会随着问题规模的增大而急剧下降，难以满足大规模布图规划的收敛性能需求。为了提高FA-COM算法的优化效率，可以通过聚类或分区策略将问题预划分若干个小规模布图问题，采用分而治之的思想来实现对大规模的布图规划问题的快速求解［7，8］；然而，对小规模问题的局部优化难以对原问题的解空间进行高效的全局探索，无法保证布图规划算法的全局收敛性。

受到VLSI全局布局的解析式优化算法的启发，FA-AOM算法采用模块的绝对坐标表示布图规划，并利用解析数学优化算法求解布图规划的解析数学规划模型，具有比FA-COM算法更低的时间复杂度［9～11］。因此，FA-AOM通常分成两个阶段：首先，在全局布图阶段对布图规划的解析优化模型进行求解，得到违背部分约束（例如部分模块重叠或越界）但综合指标最优的阶段性布图结果；然后，利用合法化技术消除全局布图结果中的约束违背，得到合法的优化布图方案。对于包括软模块的大规模固定轮廓布图规划问题，文献［10］采用基于静电场建模的泊松方程来刻画布图规划问题，并采用解析优化方法对势函数进行优化以得到全局布图结果；然后，构建水平约束图和垂直约束图消除重叠，生成满足固定轮廓约束的自动布图结果。

为了实现基于导数信息的快速解析优化，已有的FA-AOM需要对模块重叠、半周长等非光滑函数进行光滑近似，从而得到光滑的优化目标函数和约束条件。然而，FA-AOM所采用的光滑近似函数非常复杂，对函数值和导数的计算复杂度比较高；同时，近似得到光滑目标函数与原目标函数的数学性质不尽相同，可能得到与原问题具有不同最优解的近似优化模型；另外，FA-AOM常采用基于水平/垂直约束图的合法化策略消除模块重叠和越界，进一步增加了算法的时间复杂度。鉴于此，本文构建了布图规划的非光滑解析数学规划模型，并利用共轭次梯度算法（conjugate sub-gradient algorithm，CSA）［12］来实现全局布图和合法化以得到优化的布图规划结果。具体地，提出了全局布图和合法化的解析数学规划模型并利用CSA进行求解，得到了固定轮廓约束下对线长进行优化的布图规划算法CSA_FC（conjugate sub-gradient algorithm with fixed-outline constraints）和无固定轮廓约束时对面积和线长进行优化的布图规划算法CSA_GSS（conjugate sub-gradient algorithm with golden section strategy）。

1 布图规划问题的非光滑解析数学规划模型

在VLSI布图规划问题中，需要在所有矩形模块互不重叠的前提下将矩形模块放置于平面布图区域内，并对影响VLSI性能的指标如线长、面积、模块工作温度等进行优化。记V={v1，v2，…，vn}为矩形模块的集合，E={e1，e2，…，em}为线网集合。模块vi的中心坐标用（xi，yi）表示，宽与高分别用wi和hi表示，所有模块的x-坐标和y-坐标向量记作x=（x1，…，xn），y=（y1，…，yn）。

本文重点研究两类经典的布图规划问题：第一类是给定布图区域对线长指标进行优化的固定轮廓布图规划问题，第二类是同时对线长和面积两个指标进行优化的无固定轮廓约束的布图规划问题。基于此，可以建立VLSI布图规划的通用约束优化模型

3 实验结果与分析

为了验证本文的算法的性能，在著名的测试基准GSRC上进行了实验。对于所有测试电路，I/O焊盘固定在给定坐标处，所有电路的模块都是硬模块。本文的所有实验采用基于Windows操作系统的C++语言程序，处理器为AMD Ryzen 7 5800H，主频3.2 GHz，内存为16 GB。

3.1 共轭次梯度算法的收敛性能分析

本文在全局布图规划阶段以及合法化阶段均采用CSA作为优化引擎，为了解CSA对布图规划数学模型的优化效率，以GSRC测试集中的n100电路为例，分别研究了全局布图规划阶段和合法化阶段CSA的优化性能，相应目标函数值随迭代次数变化的折线图如图2所示。

图2（a）为CSA在全局布图阶段的迭代过程，令u=（x，y），黑线、红线、蓝线、绿线分别代表目标函数f1（u）、半周长线长HPWL、重叠项D（u）以及出界项B（u）的收敛曲线。在全局布图的初始阶段，算法具有较好的收敛效率，目标函数f1（u）迅速降低;同时，由于重叠项系数λ较小，算法朝着线长优化的目标迭代，HPWL快速下降而D（u）迅速增加。在迭代过程中，每50步迭代增加λ的值，在保持线长优化的同时加大对重叠的优化，D（u）指标迅速下降，而f1（u）与HPWL缓慢上升，最终趋于稳定。由于目标函数f1（u）综合了HPWL、D（u）和B（u）三个指标，在全局布图阶段，D（u）和B（u）指标难以同时降为0，需要对结果进行合法化处理。

图2（b）为合法化阶段的迭代过程，青线代表目标函数（u）。函数值呈波动下降。迭代初期步长较大，函数值波动幅度大，步长随迭代过程下降，函数值波动幅度减小，最后趋近于0。

由于基于次梯度的CSA不是目标下降算法，其局部收敛性能要弱于梯度下降类算法，优化的目标函数f1（u）在全局布局的中后期呈现出略微振荡上升的趋势，而合法化阶段的目标函数（u）则呈现振荡下降的趋势。然而，CSA具有更好的全局收敛性能，依照2.1.2节所提出的步长选取策略，CSA能够很好地求解本文所提出的布图规划模型，得到合法的布图规划结果。

3.2 固定轮廓约束的线长优化

根据给定的纵横比R，固定轮廓的宽W*与高H*采用如下计算方法［16］：

γ=S（x，y）-AA×100%

本文选择的开源布图规划器Parquet-4.5［17］与CSA_FC进行比较。其中，Parquet-4.5采用基于B*树布图表示方法，通过模拟退火算法来对布图规划的组合优化模型进行求解，模型和算法参数均采用默认设置。实验考虑纵横比R为1，1.5，2，空白率γ为15%，所有电路的最大运行次数tmax均为20，样本数p均为5。对于不同的纵横比设置（R），每组实验独立运行十次的平均半周长（HPWL）、CPU时间（CPU）和成功率（SR）如表1所示。

实验结果表明，对于小规模测试问题（n10，n30），基于解析布局表达的CSA_FC算法的算法运行时间和布图成功率略差于基于B*树表示的开源布图器Parquet-4.5，而对于规模较大的布图规划问题（n50-n300），CSA_FC的CPU时间低于Parquet-4.5。由于B*-树模型将布图规划问题转换为一个组合优化问题，当模块数量较小时，模拟退火算法能够高效地求解该组合优化问题，从而具有更高的布图规划成功率和更短程序运行时间。随着问题规模的增大，Parquet-4.5所求解的组合优化模型的解呈指数级增长，导致模拟退火算法的求解效率迅速降低；而基于次梯度的迭代机制使得CSA_FC能够更有效地搜索布图区域，从而具有更好的布图优化效率。

在固定轮廓的布图实例中，优化模型式（3）采用了重叠面积的平方根作为重叠程度衡量指标，消除了重叠面积和线长的量纲差异；同时，CSA_FC算法的迭代过程采用了先全局布图再合法化的优化机制，从而能够更好地对线长（HPWL）进行优化，对所有的测试实例上均能够得到更好的线长优化结果。

3.3 无固定轮廓约束的线长和面积优化

对于无固定轮廓约束的布图规划问题，使用CSA_GSS对线长和面积进行优化，本文进行两组实验，首先将它与Parquet-4.5以及HSA（hybrid simulated annealing algorithm）［18］进行比较。在CSA_GSS中，ε=0.2%，所有电路的最大运行次数tmax均为20，样本数p均为5。HSA采用文献［18］中的参数设置。

表1中的实验结果表明，在纵横比R=1时布图结果均能够得到最好的线长优化结果，纵横比越大，HPWL的值越大。对多数例子而言，CPU时间也随R的增大而增大。因此在无固定轮廓约束的布图实例中，布图结果的纵横比取值为R=1。对于GSRC中的每个例子，算法运行十次的线长（HPWL）、面积（S）和运行时间（CPU）的平均值如表2所示。

结合特殊的种群初始化策略和个体生成机制，HAS能够得到比Parquet-4.5更好的线长优化效果，对于小规模电路（n10，n30，n50）也能得到更小的布图面积，但布图效率随着测试电路（n100，n200，n300）模块数的增大而迅速降低，算法运行时间急剧增加。对于无边框约束的布图规划场景，CSA_GSS同样能够得到最佳的线长优化结果，随着电路规模的增大，CSA_GSS在CPU运行时间的增长幅度最小，表明基于共轭次梯度法的CSA_GSS更适用于更大规模布图规划场景。同时，GSA_GSS算法布图面积的优化结果略差于基于B*树和模拟退火算法的Parquet-4.5以及HAS。

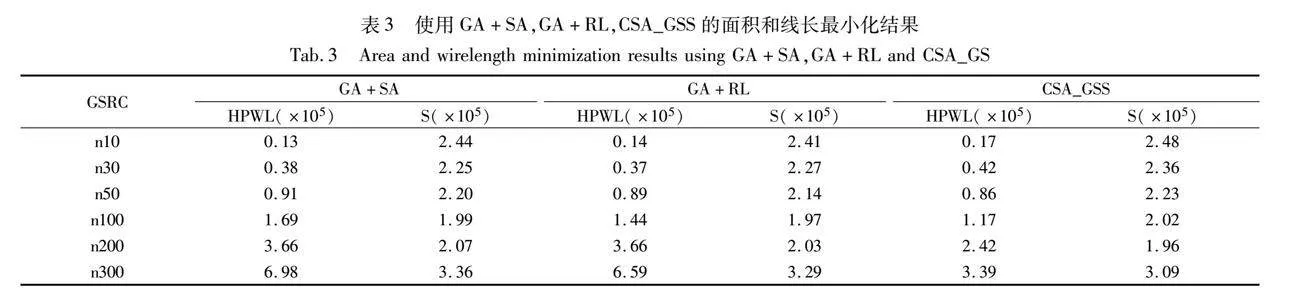
文献［19］将强化学习与遗传算法相结合，提出了GA+RL，该算法同样采用B*-树作为布图表示，利用遗传算法进行全局搜索，通过强化学习优化局部搜索策略，并与传统的GA+SA（hybrid genetic algorithm and simulated annealing）进行比较。对于线长计算，这里仅考虑模块之间的互连关系。实验数据来自文献，CSA_GSS的参数设置与上文一致。对于GSRC中的每个例子，算法运行十次的线长（HPWL）、面积（S）的平均值如表3所示。

对于n200和n300测试例子，CSA_GSS在面积和线长方面均要优于GA+SA和GA+RL。本文算法在大规模问题上具有优势，但对于小规模问题，两种比较算法均优于CSA_GSS。此外，结合强化学习策略的遗传算法相对于传统的GA+SA算法，整体上有着突出表现，具有研究潜力。图3给出了CSA_GSS对n100、n200、n300电路的一次实验布图结果。

4 结束语

针对只有硬模块的布图规划问题，本文建立了一种基于非光滑解析数学规划的布图规划模型，利用共轭次梯度法来求解带固定轮廓和无固定轮廓的布图规划问题，提出了一种基于非光滑优化的布图规划算法框架。该方法克服了基于组合优化模型的布图算法时间复杂度高的缺点，克服了基于解析数学规划模型的布图算法难以实现布图合法化的不足。实验结果表明，在只有硬模块的布图规划场景下，该布图规划算法框架能够通过统一的优化框架实现全局布图规划以及布图规划的合法化，能够更好地优化布图结果的线长。与B*树的开源软件Parquet-4.5和HAS算法相比，本文提出的基于非光滑解析优化的算法具有更低的时间复杂度，运行时间随着问题规模的增加速度远低于Parquet-4.5和HAS，有望更好地推广应用到超大规模的硬模块布图规划和布局问题中。

参考文献：

［1］Srinivasan B，Venkatesan R，Aljafari B，et al.A novel multicriteria optimization technique for VLSI floorplanning based on hybridized firefly and ant colony systems［J］.IEEE Access，2023，11：14677-14692.

［2］Weng Yifan，Chen Zhen，Chen Jianli，et al.A modified multi-objective simulated annealing algorithm for fixed-outline floorplanning［C］//Proc of IEEE International Conference on Automation，Electronics and Electrical Engineering.Piscataway，NJ：IEEE Press，2018：35-39.

［3］Chen Jianli，Zhu Wenxing.A hybrid genetic algorithm for VLSI floorplanning［C］//Proc of IEEE International Conference on Intelligent Computing and Intelligent Systems.Piscataway，NJ：IEEE Press，2010：128-132.

［4］杜世民，夏银水，储著飞，等.面向软模块的稳定固定边框布图规划算法［J］.电子与信息学报，2014，36（5）：1258-1265.（Du Shimin，Xia Yinshui，Chu Zhufei，et al.A stable fixed-outline floorplanning algorithm for soft module［J］.Journal of Electronics & Information Technology，2014，36（5）：1258-1265.）

［5］Zou Dexuan，Wang Gaige，Pan Gai，et al.A modified simulated annealing algorithm and an excessive area model for floorplanning using fixed-outline constraints［J］.Frontiers of Information Technology & Electronic Engineering，2016，17（11）：1228-1244.

［6］Ye Yin，Yin Xi，Chen Zhenyi，et al.A novel method on discrete particle swarm optimization for fixed-outline floorplanning［C］//Proc of IEEE International Conference on Artificial Intelligence and Information Systems.Piscataway，NJ：IEEE Press，2020：591-595.

［7］Yan J Z，Chu C.Defer：deferred decision making enabled fixed-outline floorplanning algorithm［J］.IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems，2010，29（3）：367-381.

［8］Ji Pengli，He Kun，Wang Zhengli，et al.A quasi-newton-based floorplanner for fixed-outline floorplanning［J］.Computers & Operations Research，2021，129：105225.

［9］Lin Jaiming，Hung Zhixiong.UFO：unified convex optimization algorithms for fixed-outline floorplanning considering pre-placed modules［J］.IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems，2011，30（7）：1034-1044.

［10］Li Ximeng，Peng Keyu，Huang Fuxing，et al.PeF：Poisson’s equation based large-scale fixed-outline floorplanning［J］.IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems，2023，42（6）：2002-2015.

［11］黄志鹏，李兴权，朱文兴.超大规模集成电路布局的优化模型与算法［J］.运筹学学报，2021，25（3）：15-36.（Huang Zhipeng，Li Xingquan，Zhu Wenxing.Optimization models and algorithms for placement of very large scale integrated circuits［J］.Operations Research Trans，2021，25（3）：15-36.）

［12］Zhu Wenxing，Chen Jianli，Peng Zheng，et al.Nonsmooth optimization method for VLSI global placement［J］.IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems，2015，34（4）：642-655.

［13］Chen Jianli，Zhu Wenxing.An analytical placer for VLSI standard cell placement［J］.IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems，2012，31（8）：1208-1221.

［14］刘浩洋，户将，李勇锋，等.最优化：建模、算法与理论［M］.北京：高等教育出版社，2020：60-66.（Liu Haoyang，Hu Jiang，Li Yongfeng，et al.Optimization：modeling，algorithm and theory［M］.Beijing：Higher Education Press，2020：60-66.）

［15］徐杰，鲁海燕，赵金金，等.拉丁超立方抽样的自适应高斯小孔成像蝴蝶优化算法［J］.计算机应用研究，2022，39（9）：2701-2708，2751.（Xu Jie，Lu Haiyan，Zhao Jinjin，et al.Self-adaptive Gaussian keyhole imaging butterfly optimization algorithm based on Latin hypercube sampling［J］.Application Research of Computers，2022，39（9）：2701-2708，2751.）

［16］Zou Dexuan，Hao Guosheng，Pan Gai，et al.An improved simulated annealing algorithm and area model for the fixed-outline floorplanning with hard modules［C］//Proc of the 3rd International Symposium on Computational and Business Intelligence.Piscataway，NJ：IEEE Press，2015：21-25.

［17］Roy J A，Adya S N，Papa D A，et al.Min-cut floorplacement［J］.IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems，2006，25（7）：1313-1326.

［18］Chen Jianli，Zhu Wenxing and Ali M.M，et al.A hybrid simulated annealing algorithm for nonslicing VLSI floorplanning［J］.IEEE Trans on Systems，Man，and Cybernetics，Part C（Applications and Reviews），2011，41（4）：544-553.

［19］Liu Ke，Gu Jian and Zhu Ziran.A hybrid reinforcement learning and genetic algorithm for VLSI floorplanning［C］//Proc of the 15th International Conference on Machine Learning and Computing.New York：ACM Press，2023：412-418.

收稿日期：2023-12-06

修回日期：2024-02-11

基金项目：深圳科技计划资助项目（JCYJ20220818102002005）；科技部科技创新2030—“新一代人工智能”重大项目（2021ZD0114600）

作者简介：孙健（1999—），男，硕士，CCF会员，主要研究方向为优化算法在电子设计自动化中的应用；徐宁（1968—），男，教授，博导，博士，主要研究方向为电子设计自动化、先进封装EDA、图像处理、人工智能；吴建（1999—），男，硕士研究生，主要研究方向为电子设计自动化；朱展洋（2001—），男，硕士研究生，主要研究方向为电子设计自动化；陈彧（1981—），男（通信作者），副教授，硕导，博士，主要研究方向为智能优化算法、电子设计自动化（ychen@whut.edu.cn）；胡建国（1977—），男，研究员，博导，博士，主要研究方向为高端集成电路设计、电子设计自动化、物联网、人工智能.