基于新颖二进制人工蜂群算法求解带权集合覆盖问题

摘 要：带权集合覆盖问题（WSCP）是一个著名的NP-hard问题。为了利用人工蜂群算法（ABC）高效求解带权集合覆盖问题，提出了一个新颖二进制ABC（记作nBABC）。在nBABC中，首先提出了随机学习和继承性相结合的全局进化算子，以提高算法的全局勘探能力。其次，基于动态调整策略提出了自适应随机取反算子，以维持勘探与开发的平衡。在借鉴近似算法的思想提出处理WSCP不可行解的修复算法WSCP-GRA和优化算法WSCP-GOA的基础上，利用nBABC给出了求解WSCP的一个新方法。为了验证nBABC求解WSCP的高效性，利用它求解OR-Library中45个WSCP实例，与多个算法的比较表明：nBABC能够求得所有实例的最优值，比已有求解WSCP的算法更具竞争力。

关键词：演化算法；带权集合覆盖问题；二进制人工蜂群算法；随机学习机制；修复与优化

中图分类号：TP301.6 文献标志码：A 文章编号：1001-3695（2024）09-022-2722-10

doi：10.19734/j.issn.1001-3695.2024.01.0015

Novel binary artificial bee colony algorithm for solving weighted set covering problem

Sun Feia，He Yichaoa，b，c，Zhang Hansonga，Li Minglianga，c，Wang Linaa，Gao Zexiana

（a.College of Information Technology，b.Hebei Key Laboratory of Optoelectronic Information & Geo-detection Technology，c.Intelligent Sensor Network Engineering Research Center of Hebei Province，Hebei GEO University，Shijiazhuang 050031，China）

Abstract：The weighted set covering problem（WSCP）is a famous NP-hard problem.In order to solve the WSCP efficiently by using artificial bee colony algorithm（ABC），this paper proposed a novel binary ABC（nBABC）.In nBABC，it proposed a global evolution operator which combined random learning and inheritance to improve the global exploration ability of the algorithm.Secondly，based on the dynamic adjustment strategy，it proposed an adaptive random inversion operator to maintain the balance between exploration and development.Based on the idea of approximate algorithm，it proposed the repair algorithm WSCP-GRA and optimization algorithm WSCP-GOA for dealing with the infeasible solution of WSCP，on the basis of which a new method for solving WSCP was given by using nBABC.In order to verify the efficiency of nBABC in solving WSCP，using it to solve 45 WSCP instances in OR-Library.The comparison with several algorithms shows that nBABC can obtain the optimal values of all instances，which is more competitive than the existing algorithms for solving WSCP.

Key words：evolutionary algorithms;weighted set covering problem;binary artificial bee colony algorithm;random learning mechanism;repair and optimization

0 引言

带权集合覆盖问题（weighted set cover problem，WSCP）［1］是一个经典的NP-hard问题，也是一个著名的组合优化问题，在无线传感器网络、测试集优化和故障诊断等［2］领域具有广泛的应用。目前，求解WSCP的算法分为精确算法和非精确算法两类。精确算法主要包括割平面法、分支限界法、拉格朗日法。由于不存在求解WSCP的多项式时间精确算法，随着实例规模的增加，精确算法的耗时极速增长，不适用于求解大规模WSCP实例。

求解WSCP的非精确算法主要包括近似算法［3～7］和演化算法［8～17］，它们都具有多项式时间复杂度。近似算法虽然不能保证求得最优解，但能够在较短的时间内获得一个相对满意的近似解。例如：Peleg等人［3］基于随机舍入技术提出了求解WSCP的一个近似算法；Chvatal［4］基于启发式贪心策略提出了近似比为ln（m）+1的近似算法（m是WSCP中的元素个数）；Ohlsson等人［5］基于平均场反馈过程人工神经网络提出了一种有效近似算法MF，该算法将近似比控制在几个百分点以内；Haddadi［6］基于拉格朗日启发式算法提出了一种求解WSCP的近似算法LHSCP；陈端兵等人［7］基于启发式贪心算法和随机跳坑策略，提出了一种求解WSCP的有效近似算法CGRA。虽然近似算法的求解速度很快，但是它们的求解结果欠佳，不足以满足实际应用的要求。

演化算法具有适应性好、鲁棒性强和易于实现等优势，利用演化算法求解WSCP已成为研究的热点。例如，Beasley等人［8］引入了修补算子和贪心策略处理WSCP的不可行解，基于遗传算法提出了求解WSCP的有效算法（记作BeGA）。BeGA不仅稳定性强，而且求解效果很好。陈亮等人［9］基于遗传算法提出了一个求解WSCP的可行方法，并利用4个WSCP实例验证了所给方法的可行性。吴志勇等人［10］建立了WSCP的一种数据约简方法，基于二阶段遗传算法提出了求解WSCP的一种有效算法TSGA。Lessing等人［11］基于不同策略提出了多个启发式信息更新方式，探讨了利用蚁群优化（ACO）求解WSCP的可行性。类似地，Ren等人［12］提出了利用ACO求解WSCP的一种可行方法。Crawford等人［13～15］分别探讨基于二进制教学优化算法、二进制萤火虫算法和二元入侵杂草优化求解WSCP的可行性。Lanza-Gutierrez等人［16］提出了二进制猫群优化BCSO，并利用它给出了一个求解WSCP的有效方法。最近，Crawford等人［17］基于二进制猴群搜索提出了求解WSCP的一个新算法IBMSAV，该算法的求解结果较好。

基于不同的灵感与思想，学者们相继提出了许多优秀的演化算法，例如粒子群优化（particle swarm optimization，PSO）［18］、差分演化（differential evolution，DE）［19］和人工蜂群算法（artificial bee colony，ABC）［20］等，并将它们成功应用于求解组合优化问题。因此，如何利用它们高效地求解WSCP是一个值得探讨的问题。其次，如何有效地处理不可行解，是利用演化算法求解WSCP的一个关键问题。然而，目前还缺少普遍且有效地处理WSCP不可行解的方法，这值得研究与探讨。为此，本文首先提出了一个新颖二进制ABC（记作nBABC），然后借鉴近似算法的思想，提出处理不可行解的一个修复算法与一个优化算法；在此基础上，利用nBABC给出了一个求解WSCP的新的高效方法。

1 背景知识

1.1 集合覆盖问题

WSCP描述为：给定一个含有m个元素的集合U={u1，u2，…，um}和U的子集族S={S1，S2，…，Sn}，∪S=U；每一个Si都具有一个非负权重ci，满足SiU且Si≠（i=1，2，…，n）。WSCP的目标是求一个S*S，使得∪S*=U且∑Sj∈S*cj最小。

4 仿真计算与比较

4.1 计算环境与测试用例

本文所有仿真计算使用的微型计算机为Dell G15笔记本，硬件配置为11th Gen IntelCoreTMi5-11260H CPU-2.61 GHz RAM 16 GB（15.7 GB可用），操作系统为Microsoft Windows 11。所有算法均采用C语言编程实现，编译环境为Visual Studio 2019。使用Python语言在Jupyter Notebook（Anaconda）环境下绘制小提琴图、折线图、柱状图、收敛曲线图和Friedman秩和检验图［37］。

仿真计算用例为OR-Library中的45个WSCP实例，它们依照矩阵规模和density（密度：矩阵中非零元素的百分比）分为7组，详细信息如表1所示。WSCP实例的命名规则为：SCPa.b，其中a表示实例集编号，b表示该实例在实例集中的序号。例如，实例SCP5.8表示实例集5中的第8个WSCP实例，它的规模为m×n=200×2000，density=2%。所有45个实例的具体数据可从http：//mscmga.ms.ic.ac.uk/info.html下载。

4.2 nBABC算法参数

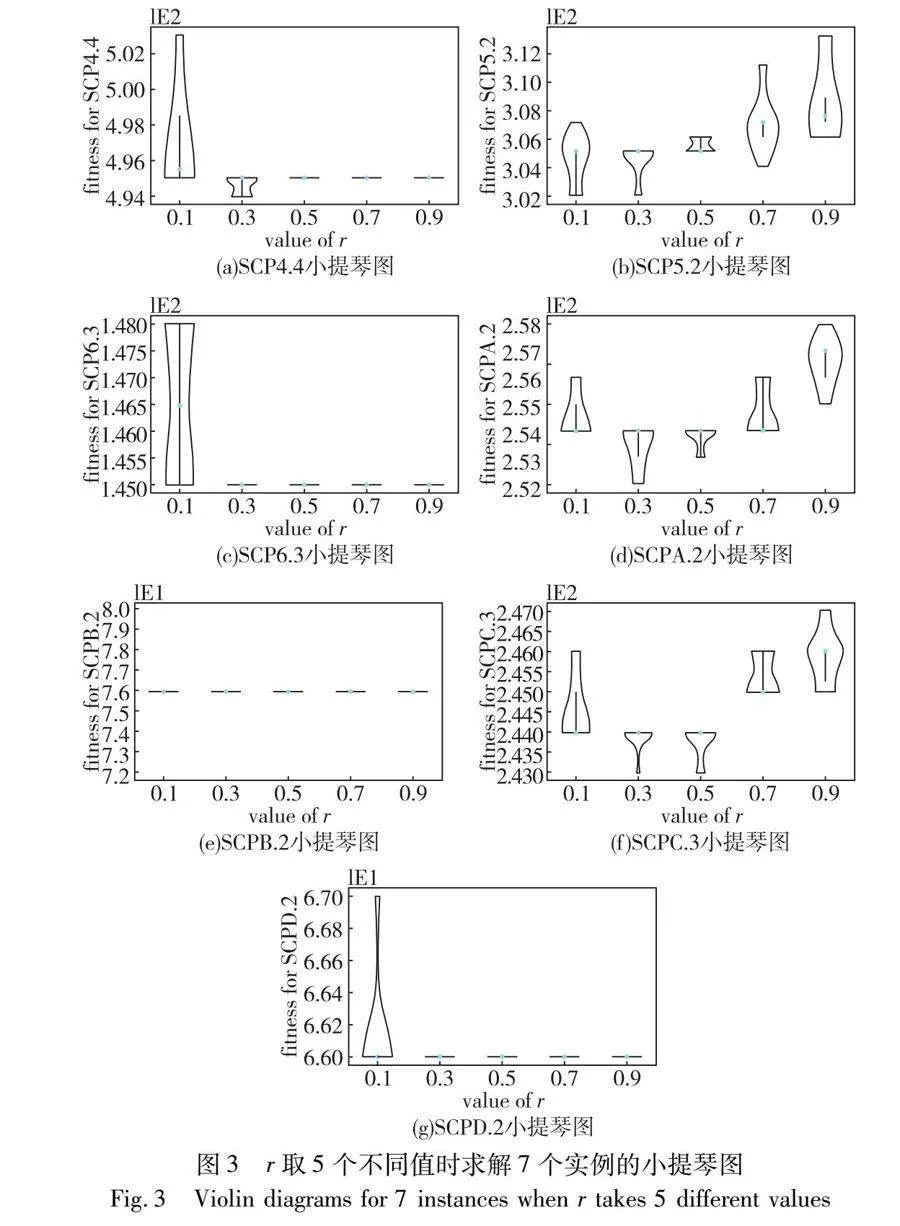
为了确定nBABC的全局进化算子中参数r的值，利用nBABC独立求解SCP4.4、SCP5.2、SCP6.3、SCPA.2、SCPB.2、SCPC.3和SCPD.2等实例各10次，根据计算结果确定r的合理取值。图3给出了r取5个代表性值0.1、0.3、0.5、0.7和0.9时，nBABC计算各实例10次所得最好结果的小提琴图，从中不难看出，当r取值0.3时，nBABC的求解性能最佳。

用类似上述的方法可以确定nBABC的全局进化算子中参数rf的最佳取值为0.7；基于动态调整策略的自适应随机取反算子中参数a1=0.1，b1=0.6，a2=0.01，b2=0.6时，nBABC的性能最佳。

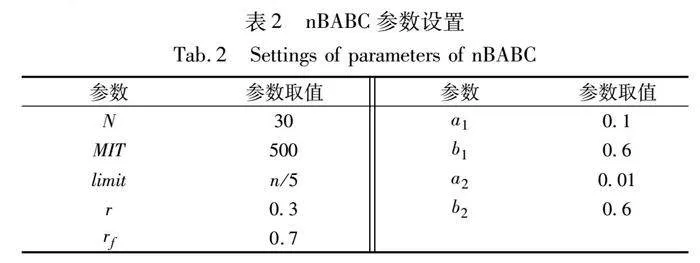
综上，在表2中给出了nBABC的参数取值，其中N为种群的规模，MIT为迭代次数，limit为蜜源转换为侦察蜂的阈值，r和rf为具有随机学习与继承的全局进化算子中的参数，a1、b1、a2、b2为基于动态调整策略的自适应随机取反算子中的参数。

4.3 比较指标

为了阐明nBABC求解WSCP的高效性，首先将它与5个优秀的二进制人工蜂群算法NBABC［30］、BitABC［32］、IbinABC［33］、KBABC［34］和HBABC［35］求解45个WSCP实例的结果进行比较。其他5个二进制人工蜂群算法与nBABC一样，均使用WSCP-GRA和WSCP-GOA处理WSCP的不可行解。其次，将nBABC与7个求解WSCP的先进算法MF［5］、LHSCP［6］、CGRA［7］、BeGA［8］、TSGA［10］、BCSO［16］、IBMSAV［17］的求解结果进行比较。

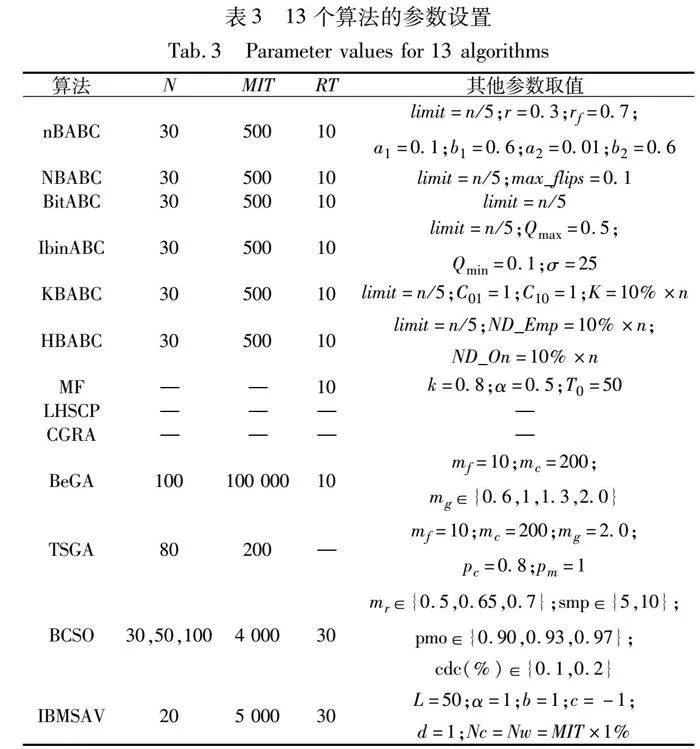
表3给出了所有13个算法的参数设置，其中N为种群规模，MIT为迭代次数，RT为每个算法独立计算各实例的次数。由于MF、LHSCP、CGRA是近似算法，不涉及参数N与MIT，这3个算法的N、MIT指标用“—”标出。各算法的参数含义请参见文献［5～8，10，16，17，30，32～35］，不再赘述。

4.4 与其他二进制人工蜂群算法的比较

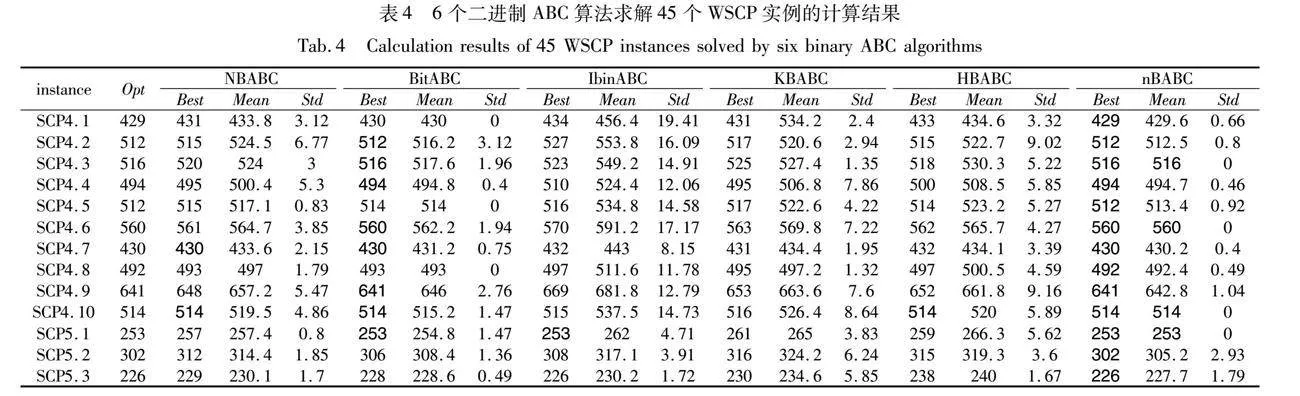
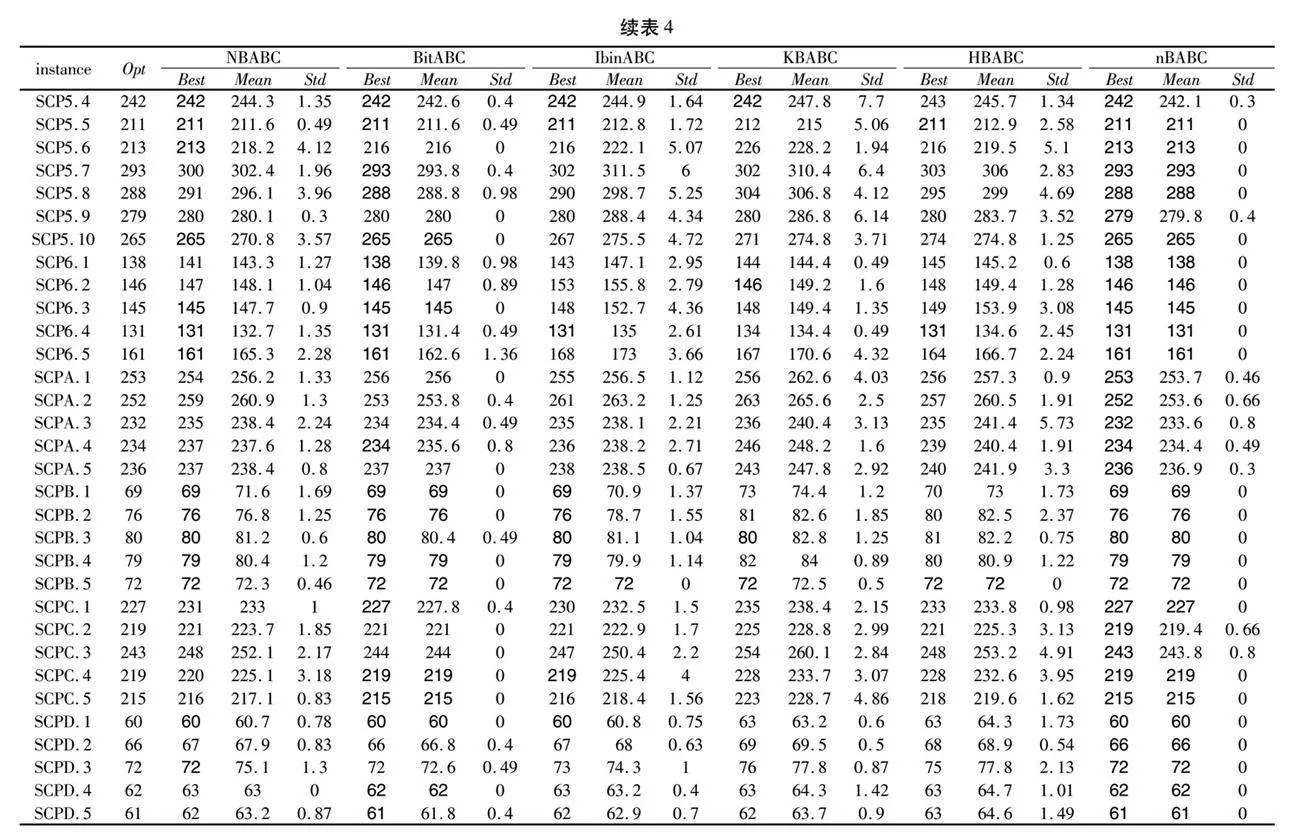
表4给出了nBABC与NBABC、BitABC、IbinABC、KBABC、HBABC求解45个WSCP实例的计算结果，其中Opt是实例的最优值，Best为各算法在10次计算中求得各实例的最好值，Mean是平均值，当Best或Mean等于Opt时加粗表示。

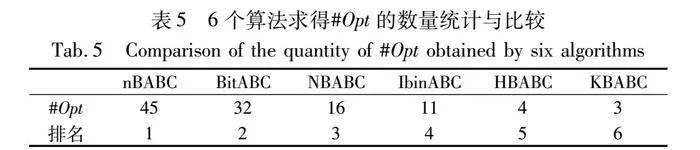
为了比较nBABC与NBABC、BitABC、IbinABC、KBABC、HBABC获得Best的优劣，令#Opt表示上述6种算法求解45个WSCP实例所能获得Opt的实例个数。从表5中可以看出：nBABC能求得所有WSCP实例的Opt，是BitABC的1.41倍，是NBABC的2.81倍，是IbinABC的4.10倍，是HBABC的11.25倍，是KBABC的15倍。以上比较结果说明，nBABC在求得Opt方面比其他的二进制ABC均优。

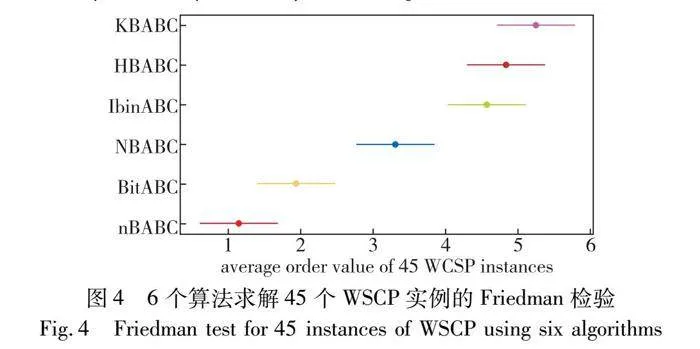
众所周知，平均性能是衡量演化算法的一个重要指标。因此根据nBABC与NBABC、BitABC、IbinABC、KBABC、HBABC求得45个WSCP实例的Mean值，在图4中利用Friedman秩和检验［37］进一步比较了四个算法的平均性能。从图4中可以看出，nBABC的平均性能最佳，其次是BitABC，并且明显优于NBABC、IbinABC、KBABC和HBABC。

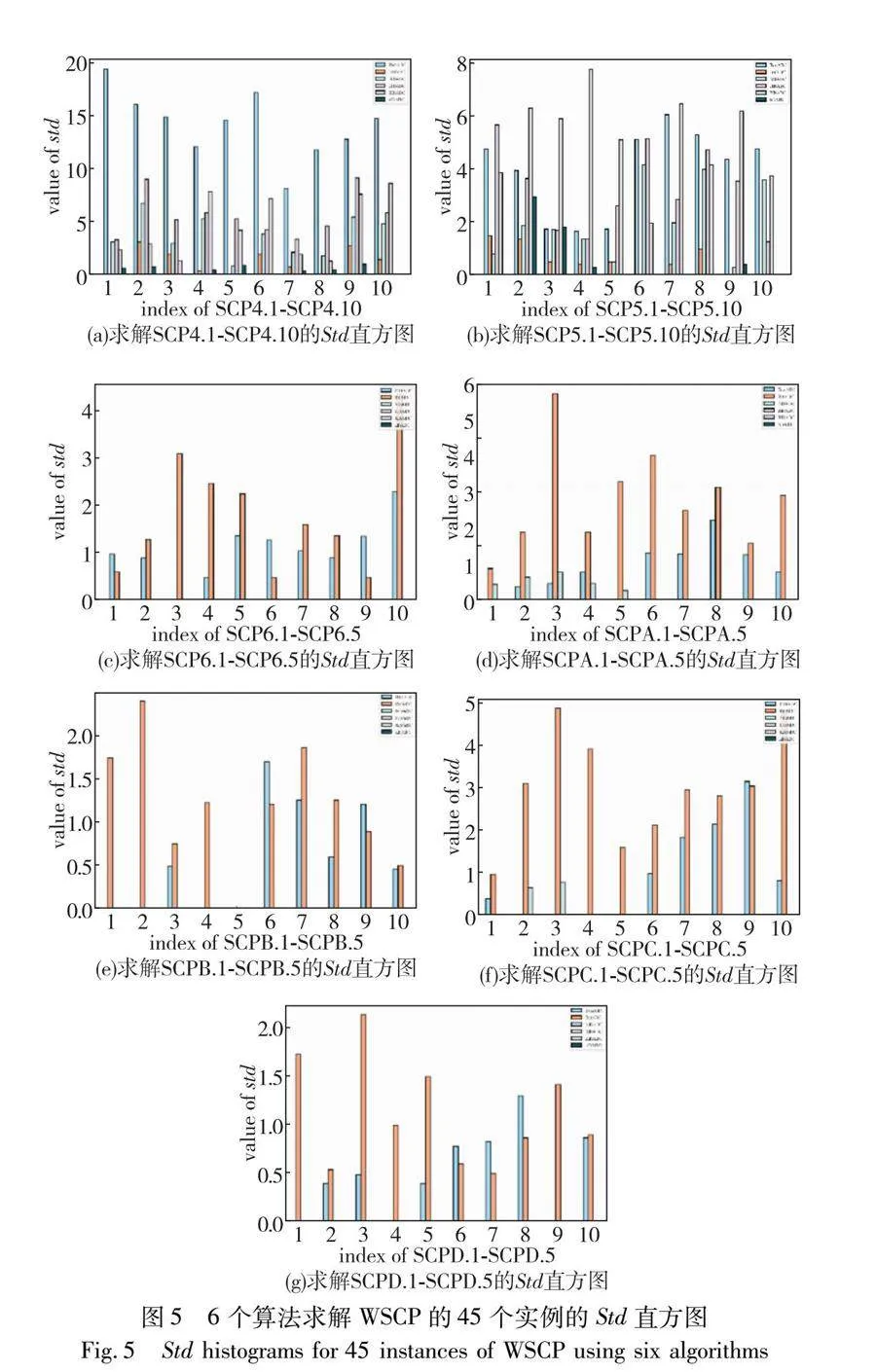
在图5中，给出了nBABC与NBABC、BitABC、IbinABC、KBABC、HBABC求解45个WSCP实例的Std的直方图。可以看出：nBABC的Std值远小于NBABC、IbinABC、KBABC和HBABC，略优于BitABC。由此说明，nBABC是这6个二进制ABC算法中稳定性最佳的。

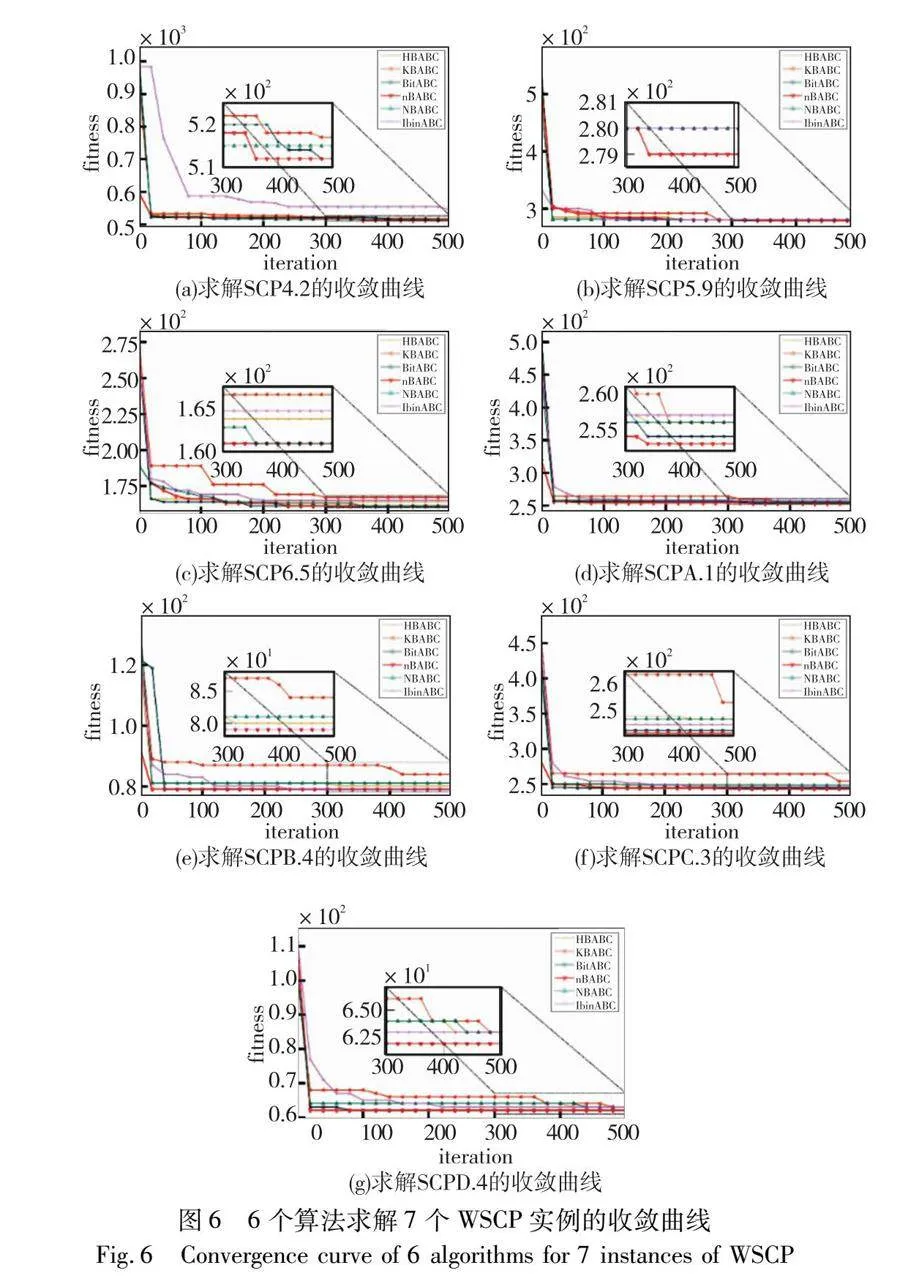
为了比较nBABC与NBABC、BitABC、IbinABC、KBABC、HBABC的收敛速度，在图6中给出了它们求解7个随机选取的WSCP实例SCP4.2、SCP5.9、SCP6.5、SCPA.1、SCPB.4、SCPC.3和SCPD.4的平均收敛曲线。可以看出：nBABC的收敛速度明显优于NBABC、BitABC、IbinABC、KBABC、HBABC，这说明nBABC不仅求解结果是最好的，而且收敛速度也是最快的。

根据上述比较可得结论：在求解WSCP时，nBABC的计算结果不仅远优于NBABC、BitABC、IbinABC、KBABC、HBABC，而且其稳定性、收敛速度也是最佳的。这表明在已有的二进制ABC算法中，nBABC是最适用于求解WSCP的。

4.5 与求解WSCP的先进演化算法的比较

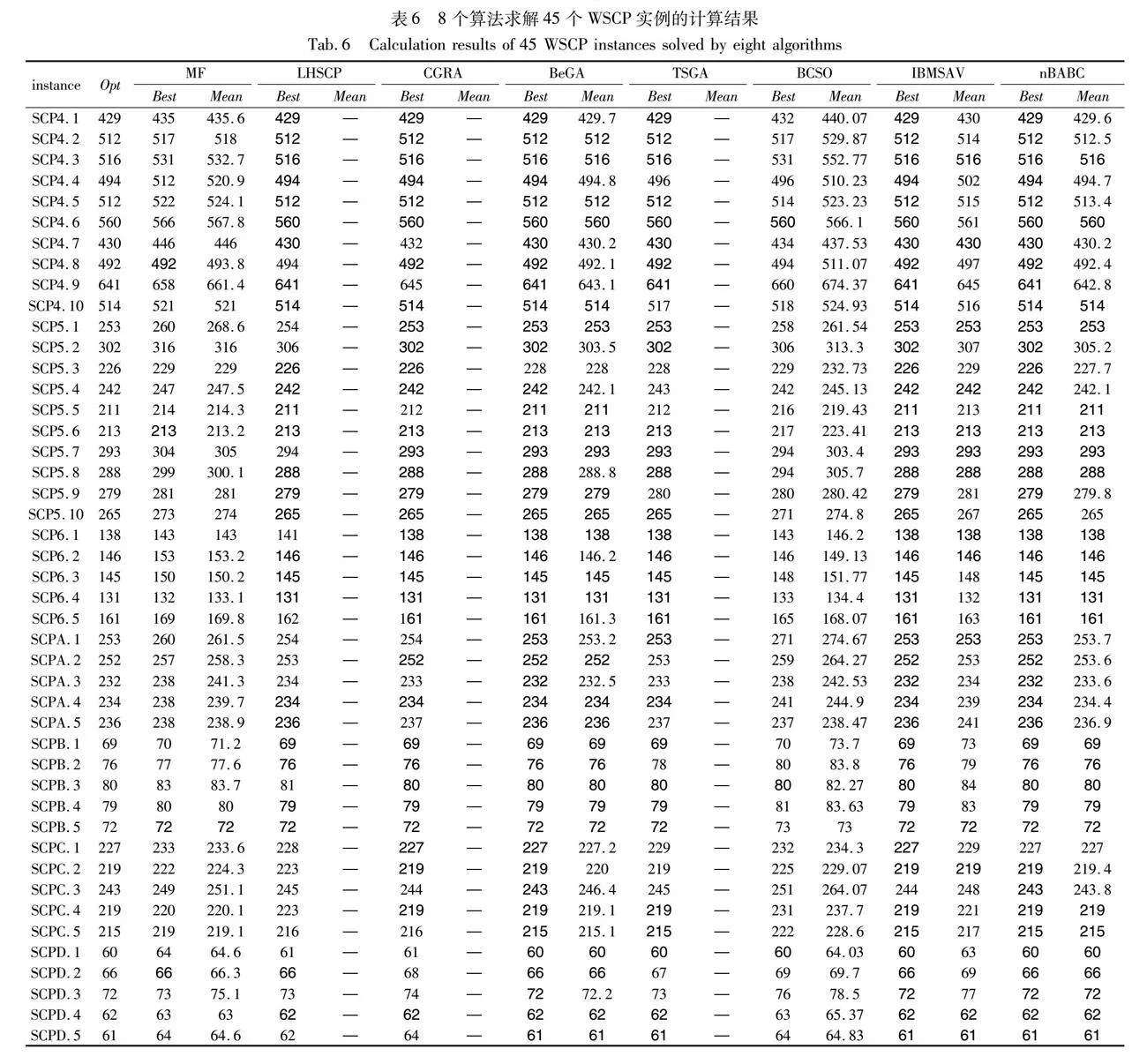
为了阐明nBABC求解WSCP的高效性能，利用nBABC求解45个WSCP实例，并与7个求解WSCP的先进算法MF、LHSCP、CGRA、BeGA、TSGA、BCSO、IBMSAV进行比较。计算结果如表6所示，由于LHSCP、CGRA和TSGA没有提供各实例的Mean，这3个算法的Mean指标用“—”标出。

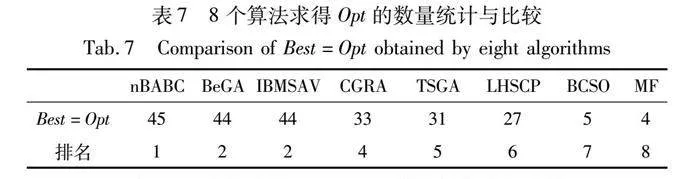
表7统计了上述8个算法求解45个WSCP实例所能获得Opt的实例个数。从中可以看出：nBABC能求得所有WSCP实例的Opt，比BeGA和IBMSAV多1个；同时，nBABC求得Opt的实例个数是CGRA的1.36倍，是TSGA的1.45倍，是LHSCP的1.67倍，是BCSO的9倍，甚至是MF的11.25倍。因此，在求得WSCP实例的最优值方面，nBABC是最优的。

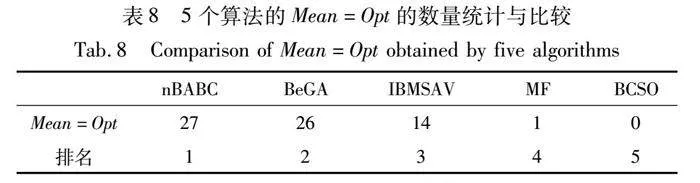
表8统计了nBABC、MF、BeGA、BCSO、IBMSAV求解45个WSCP实例中Mean等于Opt的个数。从中可以看出：nBABC求解27个WSCP实例的Mean等于Opt，比BeGA的多1个，是IBMSAV的1.9倍，是MF的27倍。BCSO不能求得任意实例的Opt。这说明nBABC的平均性能也是最佳的。

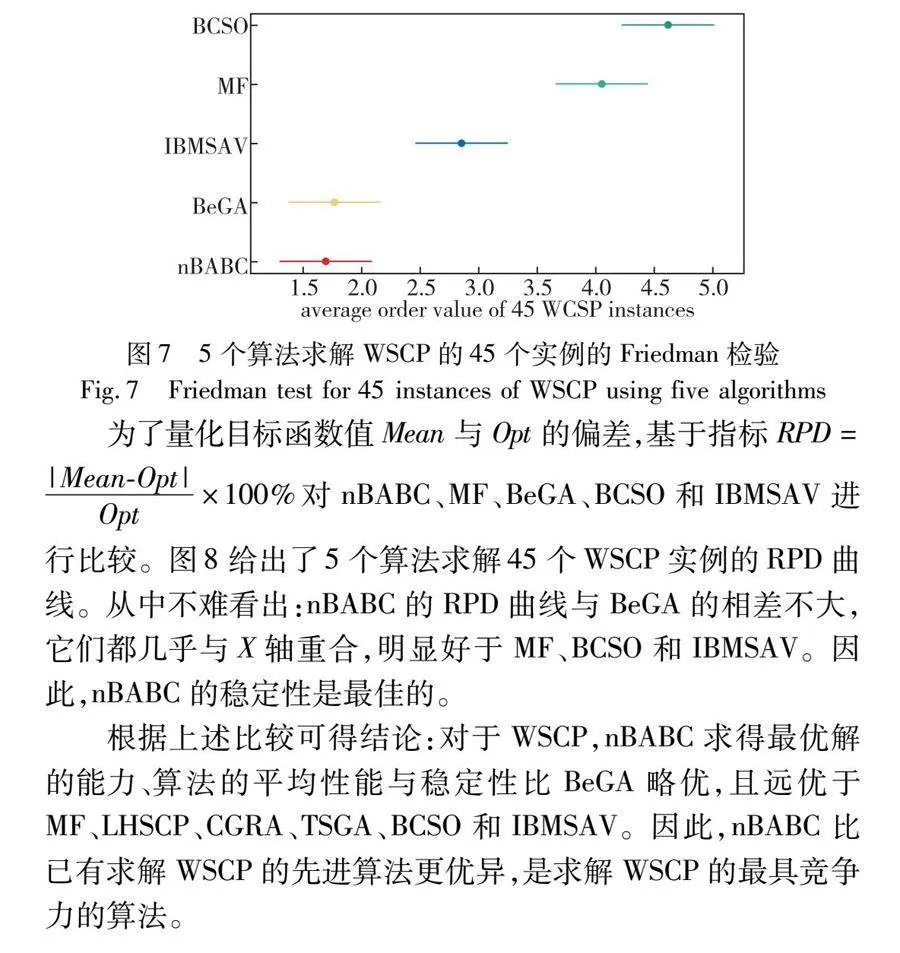
在图7中，利用Friedman秩和检验［37］对BCSO、MF、BeGA、IBMSAV和nBABC求解45个WSCP实例的平均性能的优劣进行了排序比较。从图7中不难看出：五个算法的平均性能由好到差的顺序依次是nBABC>BeGA>IBMSAV>MF>BCSO，这说明nBABC的平均性能是最佳的。

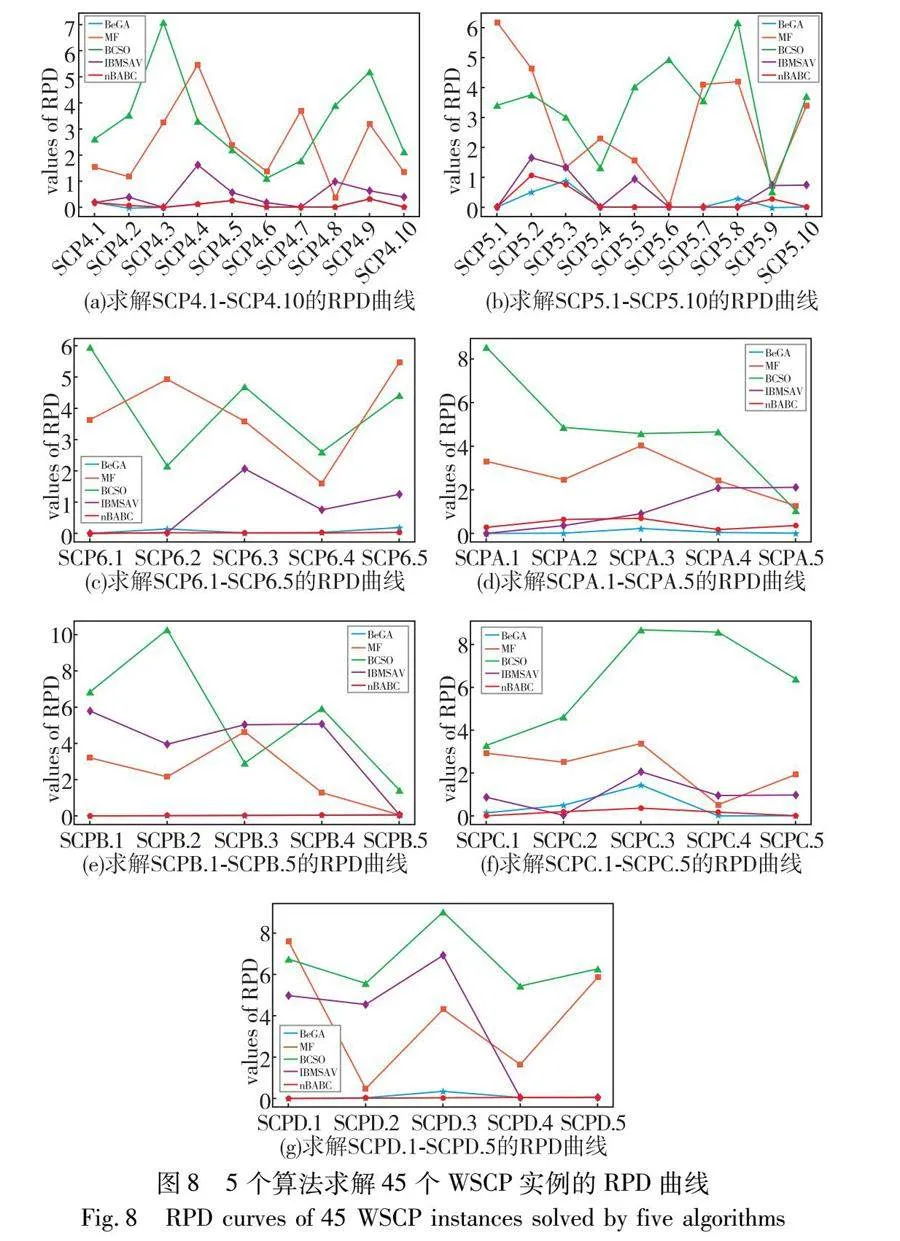
为了量化目标函数值Mean与Opt的偏差，基于指标RPD=|Mean-Opt|Opt×100%对nBABC、MF、BeGA、BCSO和IBMSAV进行比较。图8给出了5个算法求解45个WSCP实例的RPD曲线。从中不难看出：nBABC的RPD曲线与BeGA的相差不大，它们都几乎与X轴重合，明显好于MF、BCSO和IBMSAV。因此，nBABC的稳定性是最佳的。

根据上述比较可得结论：对于WSCP，nBABC求得最优解的能力、算法的平均性能与稳定性比BeGA略优，且远优于MF、LHSCP、CGRA、TSGA、BCSO和IBMSAV。因此，nBABC比已有求解WSCP的先进算法更优异，是求解WSCP的最具竞争力的算法。

5 结束语

本文首先提出了具有随机学习和继承性相结合的改进全局进化算子，其次给出了具有动态调整策略的自适应随机取反算子，由此提出了一个新的二进制人工蜂群算法nBABC。为了有效处理基于演化算法求解WSCP时所产生的不可行解，提出了修复算法WSCP-GRA和优化算法WSCP-GOA，在此基础上利用nBABC给出了一个求解WSCP的新方法。通过与5个优秀的二进制人工蜂群算法以及7个求解WSCP的先进算法的比较表明：nBABC不仅求得最优解的能力最佳，而且平均性能与稳定性也是最优的。

为了探究nBABC的实用性，今后将探讨利用它求解无线传感器网络覆盖、路径规划和测试集优化等工程问题，进一步研究nBABC的进化方程与局部优化策略，使其成为一个更高效的离散演化算法。

参考文献：

［1］Lemke C E，Salkin H M，Spielberg K.Set covering by single-branch enumeration with linear-programming subproblems［J］.Operations Research，1971，19（4）：998-1022.

［2］夏炳森，李翠，林文钦，等.基于相关矩阵和动态集合覆盖的配电网故障诊断方法［J］.重庆邮电大学学报：自然科学版，2022，34（3）：535-542.（Xia Bingsen，Li Cui，Lin Wenqin，et al.Dependency matrix and dynamic set-covering based fault diagnosis method for power distribution networks［J］.Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition，2022，34（3）：535-542.）

［3］Peleg D，Schechtman G，Wool A.Approximating bounded 0-1 integer linear programs［C］//Proc of the 2nd Israel Symposium on Theory and Computing Systems.Washington DC：IEEE Computer Society，1993：69-77.

［4］Chvatal V.A greedy heuristic for the set-covering problem［J］.Mathematics of Operations Research，1979，4（3）：233-235.

［5］Ohlsson M，Peterson C，Sderberg B.An efficient mean field approach to the set covering problem［J］.European Journal of Operational Research，2001，133（3）：583-595.

［6］Haddadi S.Simple Lagrangian heuristic for the set covering problem［J］.European Journal of Operational Research，1997，97（1）：200-204.

［7］陈端兵，黄文奇.一种求解集合覆盖问题的启发式算法［J］.计算机科学，2007，34（4）：133-136.（Chen Duanbing，Huang Wenqi.A heuristic algorithm for set covering problem［J］.Computer Science，2007，34（4）：133-136.）

［8］Beasley J E，Chu P C.A genetic algorithm for the set covering problem［J］.European Journal of Operational Research，1996，94（2）：392-404.

［9］陈亮，任世军.一种遗传算法在集合覆盖问题中的应用研究［J］.哈尔滨商业大学学报：自然科学版，2006，22（2）：67-70.（Chen Liang，Ren Shijun.Study on genetic algorithm application in set cove-ring problem［J］.Journal of Harbin University of Commerce：Na-tural Sciences Edition，2006，22（2）：67-70.）

［10］吴志勇，陈韬，王红川，等.一个解决集合覆盖问题的二阶段遗传算法［J］.小型微型计算机系统，2011，32（4）：732-737.（Wu Zhiyong，Chen Tao，Wang Hongchuan，et al.Two-stage genetic algorithm for set covering problem［J］.Journal of Chinese Computer Systems，2011，32（4）：732-737.）

［11］Lessing L，Dumitrescu I，Stutzle T.A comparison between ACO algorithms for the set covering problem［C］//Proc of International Workshop on Ant Colony Optimization and Swarm Intelligence.Berlin：Springer，2004：1-12.

［12］Ren Zhigang，Feng Zuren，Ke Liangjun，et al.New ideas for applying ant colony optimization to the set covering problem［J］.Computers & Industrial Engineering，2010，58（4）：774-784.

［13］Crawford B，Soto R，Aballay F，et al.A teaching-learning-based optimization algorithm for solving set covering problems［C］//Proc of the 15th International Conference on Computational Science and Its Applications.Cham：Springer，2015：421-430.

［14］Crawford B，Soto R，Suárez M O，et al.Binary firefly algorithm for the set covering problem［C］//Proc of the 9th Iberian Conference on Information Systems and Technologies.Piscataway，NJ：IEEE Press，2014：1-5.

［15］Crawford B，Soto R，Legüe I F，et al.A binary invasive weed optimization algorithm for the set covering problem［C］//Proc of the 5th Computer Science On-Line Conference on Artificial Intelligence Perspectives in Intelligent Systems.Cham：Springer，2016：459-468.

［16］Lanza-Gutierrez J M，Crawford B，Soto R，et al.Analyzing the effects of binarization techniques when solving the set covering problem through swarm optimization［J］.Expert Systems with Applications，2017，70：67-82.

［17］Crawford B，Soto R，Olivares R，et al.A binary monkey search algorithm variation for solving the set covering problem［J］.Natural Computing，2020，19（4）：825-841.

［18］Yazdani Delaram，Yazdani Danial，Yazdani Donya，et al.A species-based particle swarm optimization with adaptive population size and deactivation of species for dynamic optimization problems［J］.ACM Trans on Evolutionary Learning and Optimization，2023，3（4）：1-25.

［19］Li Yanchi，Gong Wenyin，Li Shuijia.Evolutionary competitive multitasking optimization via improved adaptive differential evolution［J］.Expert Systems with Applications，2023，217：119550.

［20］Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization：artificial bee colony（ABC）algorithm［J］.Journal of Global Optimization，2007，39：459-471.

［21］Xu Feiyi，Li Haolun，Pun Chiman，et al.A new global best guided artificial bee colony algorithm with application in robot path planning［J］.Applied Soft Computing，2020，88：106037.

［22］Wei Qu，Guo Zhaoxia，Lau H C，et al.An artificial bee colony-based hybrid approach for waste collection problem with midway disposal pattern［J］.Applied Soft Computing，2019，76：629-637.

［23］ztürk，Ahmad R，Akhtar N.Variants of artificial bee colony algorithm and its applications in medical image processing［J］.Applied Soft Computing，2020，97：106799.

［24］可晓东，陶翼飞，罗俊斌，等.反向人工蜂群算法求解混合流水车间调度问题［J］.计算机应用研究，2023，40（4）：1075-1079，1087.（Ke Xiaodong，Tao Yifei，Luo Junbin，et al.Opposite artificial bee colony algorithm for hybrid flow shop scheduling problem［J］.Application Research of Computers，2023，40（4）：1075-1079，1087.）

［25］李瑞，徐华，杨金峰，等.改进近邻人工蜂群算法求解柔性作业车间调度问题［J］.计算机应用研究，2024，41（2）：438-443.（Li Rui，Xu Hua，Yang Jinfeng，et al.Improved algorithm of near-neighbor artificial bee colony for flexible Job-Shop scheduling［J］.Application Research of Computers，2024，41（2）：438-443.）

［26］Pampará G，Engelbrecht A P.Binary artificial bee colony optimization［C］//Proc of IEEE Symposium on Swarm Intelligence.Piscataway，NJ：IEEE Press，2011：1-8.

［27］Kiran M S.The continuous artificial bee colony algorithm for binary optimization［J］.Applied Soft Computing，2015，33：15-23.

［28］Hancer E，Xue Bing，Karaboga D，et al.A binary ABC algorithm based on advanced similarity scheme for feature selection［J］.Applied Soft Computing，2015，36：334-348.

［29］Ozturk C，Hancer E，Karaboga D.Dynamic clustering with improved binary artificial bee colony algorithm［J］.Applied Soft Computing，2015，28：69-80.

［30］Jr Santana C J，Macedo M，Siqueira H，et al.A novel binary artificial bee colony algorithm［J］.Future Generation Computer Systems，2019，98：180-196.

［31］Kiran M S，Gündüz M.XOR-based artificial bee colony algorithm for binary optimization［J］.Turkish Journal of Electrical Engineering and Computer Sciences，2013，21（8）：2307-2328.

［32］Jia Dongli，Duan Xintao，Khan M K.Binary artificial bee colony optimization using bitwise operation［J］.Computers & Industrial Engineering，2014，76：360-365.

［33］Durgut R.Improved binary artificial bee colony algorithm［J］.Frontiers of Information Technology & Electronic Engineering，2021，22（8）：1080-1091.

［34］Kiran M S.A binary artificial bee colony algorithm and its performance assessment［J］.Expert Systems with Applications，2021，175：114817.

［35］Hakli H.The optimization of wind turbine placement using a binary artificial bee colony algorithm with multi-dimensional updates［J］.Electric Power Systems Research，2023，216：109094.

［36］柴岩，孙笑笑，任生.融合多向学习的混沌麻雀搜索算法［J］.计算机工程与应用，2023，59（6）：81-91.（Chai Yan，Sun Xiaoxiao，Ren Sheng.Chaotic sparrow search algorithm based on multi-directional learning［J］.Computer Engineering and Applications，2023，59（6）：81-91.）

［37］Derrac J，García S，Molina D，et al.A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms［J］.Swarm and Evolutionary Computation，2011，1（1）：3-18.

收稿日期：2024-01-08

修回日期：2024-03-04

基金项目：河北省自然科学基金资助项目（F2020403013）；河北省高等学校科学技术研究项目（ZD2021016）；河北省重点研发计划资助项目（22375415D）；河北省研究生创新能力培养资助项目（CXZZSS2014109）

作者简介：孙菲（1998—），女，河北邢台人，硕士研究生，主要研究方向为演化算法及其应用；贺毅朝（1969—），男（通信作者），河北晋州人，教授，硕导，主要研究方向为演化算法、组合优化（heyichao@hgu.edu.cn）；张寒崧（1999—），男，河北邯郸人，硕士研究生，主要研究方向为演化算法与组合优化；李明亮（1976—），男，河北井陉人，教授，硕导，博士，主要研究方向为演化算法、物联网技术；王丽娜（1999—），女，河北唐山人，硕士研究生，主要研究方向为演化算法及其应用；高泽贤（1997—），女，河北石家庄人，硕士研究生，主要研究方向为演化算法及其应用.