结合精英初始化和K近邻的蛇优化算法

摘 要：蛇优化算法（SO）是一种受自然界中蛇生存行为启发产生的元启发式优化算法。原始蛇优化算法存在收敛速度慢、易陷入局部最优的问题，因此提出了一种结合精英初始化和K近邻的改进蛇优化算法（elite initia-lization and K-nearest neighbors improved snake optimizer，EKISO）。首先，为了提高初始种群质量，在种群初始化阶段提出精英初始化的方法，根据种群精英个体产生优质初始种群个体；其次，通过振荡因子优化螺旋觅食策略扩大全局勘探阶段的搜索范围、提高算法的局部逃逸能力；最后，在局部开发阶段提出K近邻思想的位置更新方法，增强种群个体之间的信息交互能力，从而加快收敛速度、提高收敛精度。利用14个经典测试函数和4个CEC2017测试函数将该方法与其他7种优化算法进行对比，证明EKISO收敛速度更快、精度更高且不易陷入局部最优。为了进一步验证EKISO的实用性与可行性，将EKISO应用于压力容器设计问题中，通过实验对比分析可知，EKISO在处理实际优化问题上具有一定的优越性。

关键词：蛇优化算法；精英初始化；K近邻；振荡因子；工程优化

中图分类号：TP301.6 文献标志码：A 文章编号：1001-3695（2024）09-021-2712-10

doi：10.19734/j.issn.1001-3695.2024.01.0019

Snake optimization algorithm combining elite initialisation and K-nearest neighbors

Wang Lijuan1，Liu Shuhan1，Wang Jian2，Tian Yaqi1

（1.School of Electrical Engineering，North China University of Water Resources & Electric Power，Zhengzhou 450045，China;2.School of Artificial Intelligence & Automation，Huazhong University of Science & Technology，Wuhan 430074，China）

Abstract：The survival behavior of snakes in nature generates the snake optimization（SO），a meta-heuristic optimization algorithm.But the original snake optimization algorithm suffers from slow convergence and easy to fall into the local optimum，so this paper proposed an improved snake optimization algorithm that combined elite initialization and K-nearest neighbors improved snake optimizer（EKISO）.Firstly，in order to improve the quality of the initial population，it proposed elite initialization during the population initialization stage，which generated high-quality initial population individuals based on elite individuals of the population.Secondly，optimizing the spiral foraging strategy with a shock factor expanded the search range during the global exploration stage and enhanced the algorithm’s local escape capability.Finally，in the local exploitation stage，it proposd a position update method based on the K-nearest neighbor concept，enhancing the information interaction capability among population individuals，thus accelerating convergence speed and improving convergence accuracy.This method compard with seven other optimization algorithms using 14 classical test functions and 4 CEC2017 test functions，which proves that EKISO converges faster，has higher accuracy and is not easy to fall into local optimum.To further validate the practicality and feasibility of EKISO，this paer applied it to pressure vessel design problems.Experimental comparative analysis reveals that EKISO possesses certain advantages in dealing with real optimization problems.

Key words：snake optimizer algorithm（SO）;elite initialisation;K-nearest neighbors;oscillation factor;engineering optimisation

0 引言

在工程设计［1］、调度优化［2］、电力系统［3］等领域中都会出现优化问题。目前，优化问题的复杂性不断增加，这类问题具有非线性、多目标、离散、高维、不确定性和非凸区域等特点［4，5］，因此，传统的优化方法很难处理这类问题。随着人工智能和机器学习的进步，元启发式优化算法不断被提出并能很好地解决上述具有多目标、高维、非凸区域等特点的问题［6～9］。

元启发式算法是基于计算智能机制求解优化问题的方法，能够在特定问题特征的引导下提炼相应的特征模型，从而设计出各种优化算法。元启发式算法主要分为以下四类：a）基于进化法则的算法，常见的有遗传算法（genetic algorithm，GA）［10］、差分进化算法（differential evolution algorithm，DE）［11］等，这类算法模拟了大自然中生物优胜劣汰的进化操作，但并不适用于所有类型的优化问题，某些问题的特性与进化算法的基本假设不符，可能导致算法性能不佳；b）基于群体智能的算法，常见的有粒子群算法（particle swarm optimization，PSO）［12］、侏儒猫鼬优化算法（dwarf mongoose optimization，DMO）［13］等，这类算法基于种群中个体的协同行为对目标问题进行寻优，通常需要调整一些参数，如学习因子、衰减因子等，参数的选择对算法的性能影响较大，但确定参数值可能需要大量实验佐证；c）基于人类的算法，常见的算法有教学优化算法（teaching-learning-based optimization algorithm，TLBO）［14］、帝国主义竞争算法（imperia-list competitive algorithm，ICA）［15］等，这类算法主要受到人类的教学、社交、学习、情感等行为启发而被提出，由于算法规则基于人类行为，一些问题的特性可能与这些规则不符，导致算法性能不佳；d）基于物理和化学的算法，常见的算法有水循环算法（water cycle algorithm，WCA）［16］、黑洞算法（black hole algorithm，BHA）［17］等，这类算法受宇宙中的物理规则和化学反应启发而被提出，许多算法需要调整温度、步长等参数，确定参数过程增加了算法的寻优难度。

元启发算法虽然可以解决优化问题，但是也存在收敛时间较长、容易陷入局部最优等问题。为了解决这些问题，许多学者对算法进行了改进。Zhang等人［18］提出了一种具有混合迁移算子和反馈差分进化机制的生物地理学优化算法新变体（HFBBO），能够有效解决高维优化问题。混合迁移算子使得算法能够在局部搜索和全局搜索之间自由切换，反馈差分进化机制替代随机变异算子能够帮助算法选择变异模式，避免陷入局部最优。Xia等人［19］提出了一种自适应差分进化算法，将整个种群划分为不同的子种群并根据需要选择不同的育种策略，使算法能够在不同的演化阶段合理分配计算资源，满足各种环境需求，提高了差分进化算法的性能。Liu等人［20］提出了一种启发式机制的蚁群算法新变体（IHMACO），包含适应性信息素浓度设置、改进的伪随机转移策略、具有方向判断的启发式机制以及信息素蒸发速率的动态调整四种改进机制。相比于原始蚁群算法，IHMACO具有更高的搜索效率和更强的全局搜索能力，能避免陷入局部最优。Ma等人［21］在传统的教学优化算法中引入一种新的种群机制，在教学阶段根据班级的平均成绩将所有学生分为两组并提出不同的更新策略，在学习阶段将所有学生中表现较好的一半分为一组、其余的学生分为另一组，再次采用不同的更新策略，实验结果证明改进的教学优化算法具有更高质量的解决方案和更快的收敛速度。

蛇优化算法（snake optimizer，SO）［22，23］是一种元启发式算法，SO通过模拟自然界中蛇的觅食和交配等行为来解决优化问题。SO能够平衡探索阶段和开发阶段，其求解精度较高。但是它仍存在一些问题，例如在迭代的前半部分过于专注于探索，导致SO的收敛速度变慢，在开发阶段容易陷入局部最优。针对这些问题，占宏祥等人［24］提出一种融合反向学习机制与差分进化策略的蛇优化算法（ISO），提高了算法的收敛速度和局部逃逸能力。Yao等人［25］通过引入参数动态更新策略、正余弦复合扰动因子、Tent混沌和柯西突变，提出了一种增强的蛇形优化器（ESO），实验证明ESO显著提高了算法性能和解决实际问题的能力。

本文提出一种结合精英初始化和K近邻的改进蛇优化算法（EKISO）。针对SO种群初始化存在重复性、遍历性不强的问题，在种群初始化阶段提出精英初始化方法，在初始种群中选取适应度值最小的前n个个体作为精英个体，再根据种群精英个体产生更加优质初始种群个体，以提高初始种群质量。为了防止算法陷入局部最优，在全局勘探阶段采用包含振荡因子的螺旋觅食策略进行位置更新，设计的振荡因子的波动范围不随迭代次数增加而减小，有效扩大了搜索范围，提高了算法的局部逃逸能力。为了能够充分利用个体有效信息并加快算法收敛速度，在局部开发阶段提出K近邻思想的位置更新方法，将个体与周围距离最小的K个个体视为邻居，找到比该个体适应度值小的邻居，增强种群个体与其周围邻居之间的信息交互能力，采用新的位置更新方法加快收敛速度，提高收敛精度。

本文的主要贡献如下：a）提出一种精英初始化的方法，将种群适应度最小的前n个优质个体称为精英个体，根据精英个体位置再次产生新个体，提高算法初始种群的质量、加速算法收敛；b）在螺旋觅食策略中引入振荡因子，扩大算法的全局搜索范围、提高算法的局部逃逸能力，通过K近邻方法增加个体之间的信息交互，提高个体有效信息的利用率，使算法在局部开发阶段具有更快的收敛速度和更高的收敛精度。

1 原始蛇优化算法

原始蛇优化算法首先根据式（1）随机生成蛇初始种群N。

K近邻方法使每条蛇个体能与其附近的邻居进行有效的信息交互，加强雄蛇和雌蛇之间跨性别的信息传递，有效缩短了算法的寻优时间，有利于帮助算法更快寻找到最优解。每个个体包含的有效信息都能被其他个体获取，因此能够避免算法陷入局部最优，从而达到更高的收敛精度。

2.4 改进蛇优化算法流程步骤

改进蛇优化算法的流程步骤如下：首先根据精英初始化方法产生初始种群N；接着利用加入振荡因子的螺旋觅食策略进行全局勘探；最后在局部开发阶段，利用K近邻信息共享使得算法快速收敛。

算法 改进蛇优化算法

输入：种群个体数量N；搜索范围上、下限Xmax、Xmin；最大迭代次数T；个体维度dim；近邻参数K。

输出：最优位置Xfood；最优适应度值f（Xfood）。

a）根据式（1）（14）（15）得到改进蛇优化算法的初始种群C；

b）将适应度值小的前N/2个个体划分为雌性种群Nf，剩余个体为雄性种群Nm；

c）while（t≤T）do

d） 根据雄性和雌性个体的适应度函数值，分别找到最佳雄性和雌性个体位置fbest，m、fbest，f，以及当前食物位置ffood；

e） 定义温度Temp、食物量Q；

f） if（Q<0.25）then

g） 根据式（6）对雄性和雌性蛇的位置进行更新，并计算位置更新后个体的适应度值；

h） 再根据式（20）对雄性和雌性蛇的位置进行更新，并计算位置更新后个体的适应度值；

i） 比较步骤g）h）得到的位置更新后个体的适应度值大小，保留适应度函数值较小所对应的个体位置；

j） else if（Temp>0.6）then

k） 比较个体与周围个体适应度值大小，找到每个雄性和雌性的K近邻居，保留适用度值小于该个体的邻居；

l） 根据式（23）得到个体的平均位置，再次根据式（8）对雄性和雌性的个体位置和平均位置进行更新，并计算位置更新后个体的适应度值；

m） 比较个体位置更新和平均位置更新后的适应度值大小，保留适应度函数值较小所对应的个体位置；

n） else

o） if（rand>0.6）then

p） 根据式（9）进行战斗模式下的雄性和雌性蛇个体位置更新；

q） else

r） 根据式（11）进行交配模式下的雄性和雌性蛇个体位置更新；

s） 产生子代并根据式（13）替代雄性和雌性种群中适应度值最差的个体；

t） end if

u） end if

v）end while

w）得到雄性和雌性种群中最佳位置以及对应的适应度值。

2.5 改进蛇优化算法时间复杂度分析

SO初始化种群的时间复杂度为O（N×d），其中N表示种群大小、d表示问题的维度。计算每个个体适应度值的时间复杂度是O（N），选择适应度函数值最小的个体的时间复杂度是O（N），个体位置更新的时间复杂度是O（N×d）。因此，SO总体时间复杂度为O（N×d×T），其中T表示最大迭代次数。

与SO相比，EKISO增加了以下几个部分：在精英初始化部分，计算初始化种群的适应度值的时间复杂度是O（N），生成精英个体的时间复杂度是O（N）；全局勘探阶段，使用包含振荡因子的螺旋觅食策略的时间复杂度是O（N×d）；局部开发阶段，使用K近邻信息共享策略的时间复杂度是O（N log N）；在全局和局部阶段与原始SO的输出结果进行比较，所需的时间复杂度是O（N×d）。因此，最终EKISO时间复杂度为O（N×d×T），与SO的时间复杂度相等。虽然EKISO增加了几种改进策略，但未增加算法的时间复杂度。

3 实验结果与分析

3.1 实验设计

在14个经典测试函数和4个CEC2017测试函数上，将改进蛇优化算法（EKISO）与原始蛇优化算法（SO）、遗传算法（GA）、粒子群算法（PSO）、樽海鞘群算法（salp swarm algorithm，SSA）［27］、蜻蜓优化算法（dragonfly algorithm，DA）［28］、正余弦优化算法（sine cosine algorithm，SCA）［29］、阿里巴巴与四十大盗优化算法（Ali Daba And The Forty Thieves，AFT）［30］7种优化算法进行寻优性能的比较。

为保证实验的公平性，每种算法种群数量N均设为30，7种对比算法中的参数均为默认值。每种算法在每个测试函数上的最大迭代次数T均设为500，并独立运行30次。EKISO中精英初始化方法的n=5、a取0.3，经过实验发现，参数K在［5，15］时算法的寻优效果最好，本文取K=10。EKISO相关参数如表1所示。所有算法均在同一实验平台上运行，实验的硬件环境为AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz，软件使用的是Windows 11操作系统的MATLAB R2020a。

3.2 经典测试函数结果分析

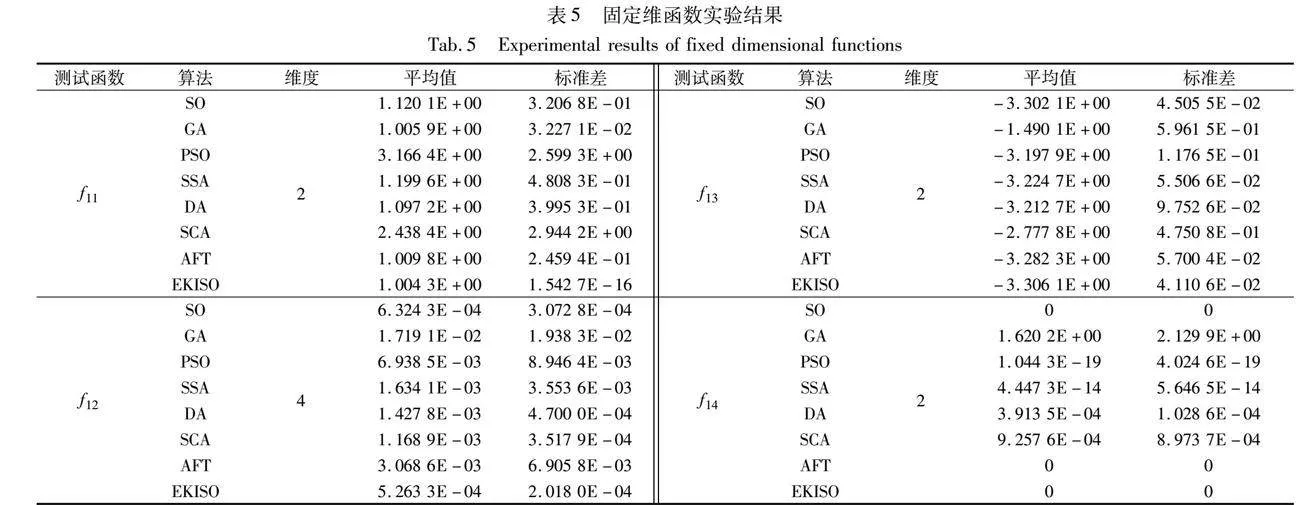
14个经典测试函数详情见表2。f1～f6为单峰函数，f7～f10为多峰函数，f11～f14为固定维函数。实验结果包含平均值（average，Avg）和标准差（standard deviation，Std），平均值验证算法的寻优能力，标准差验证算法优化过程的稳定性。

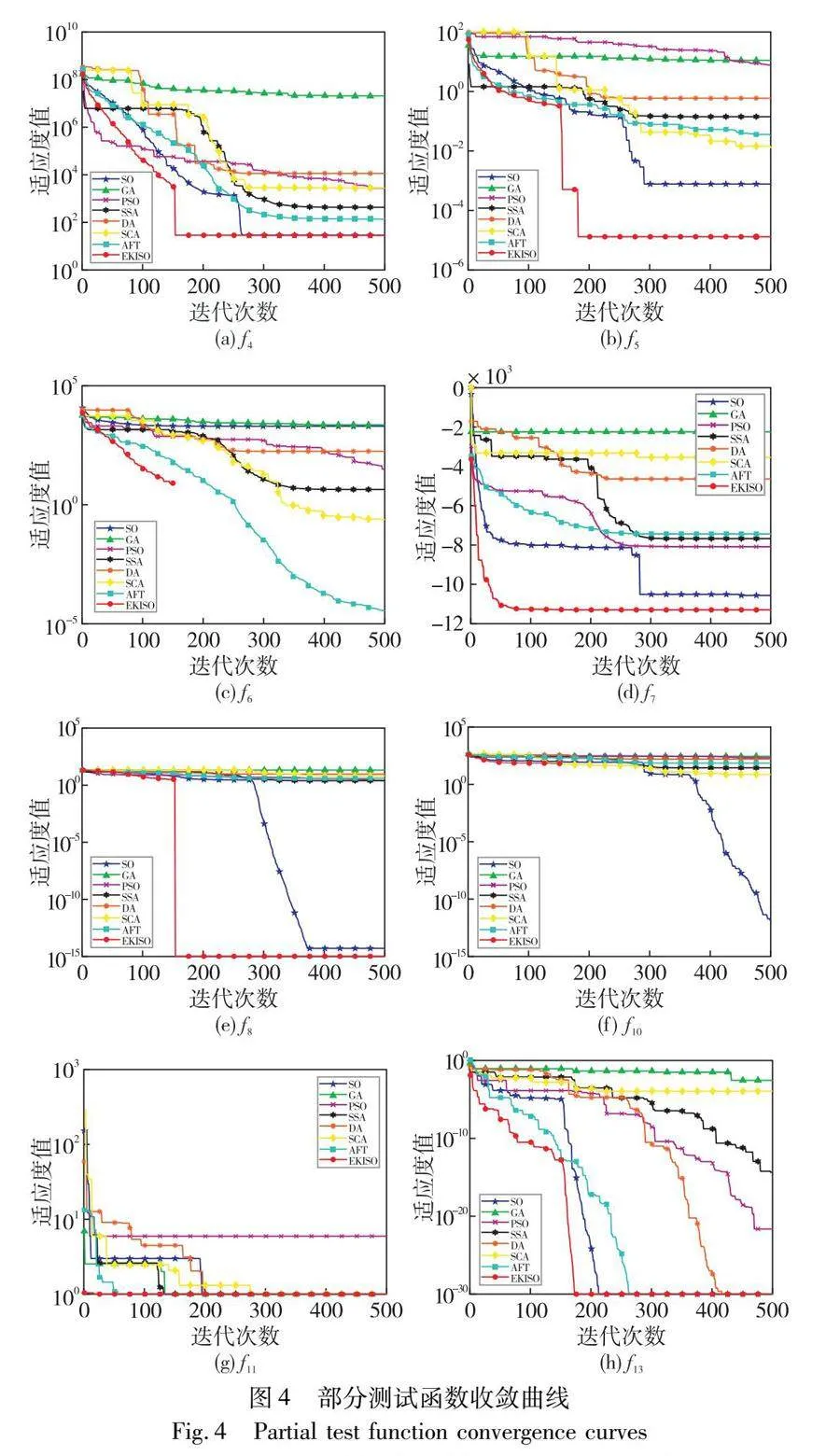
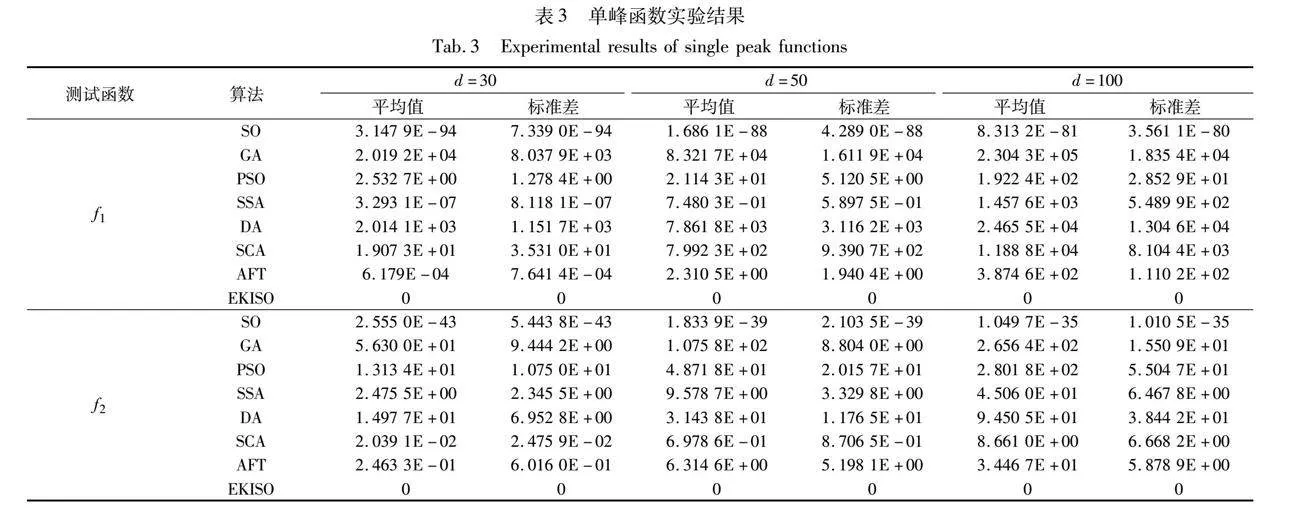
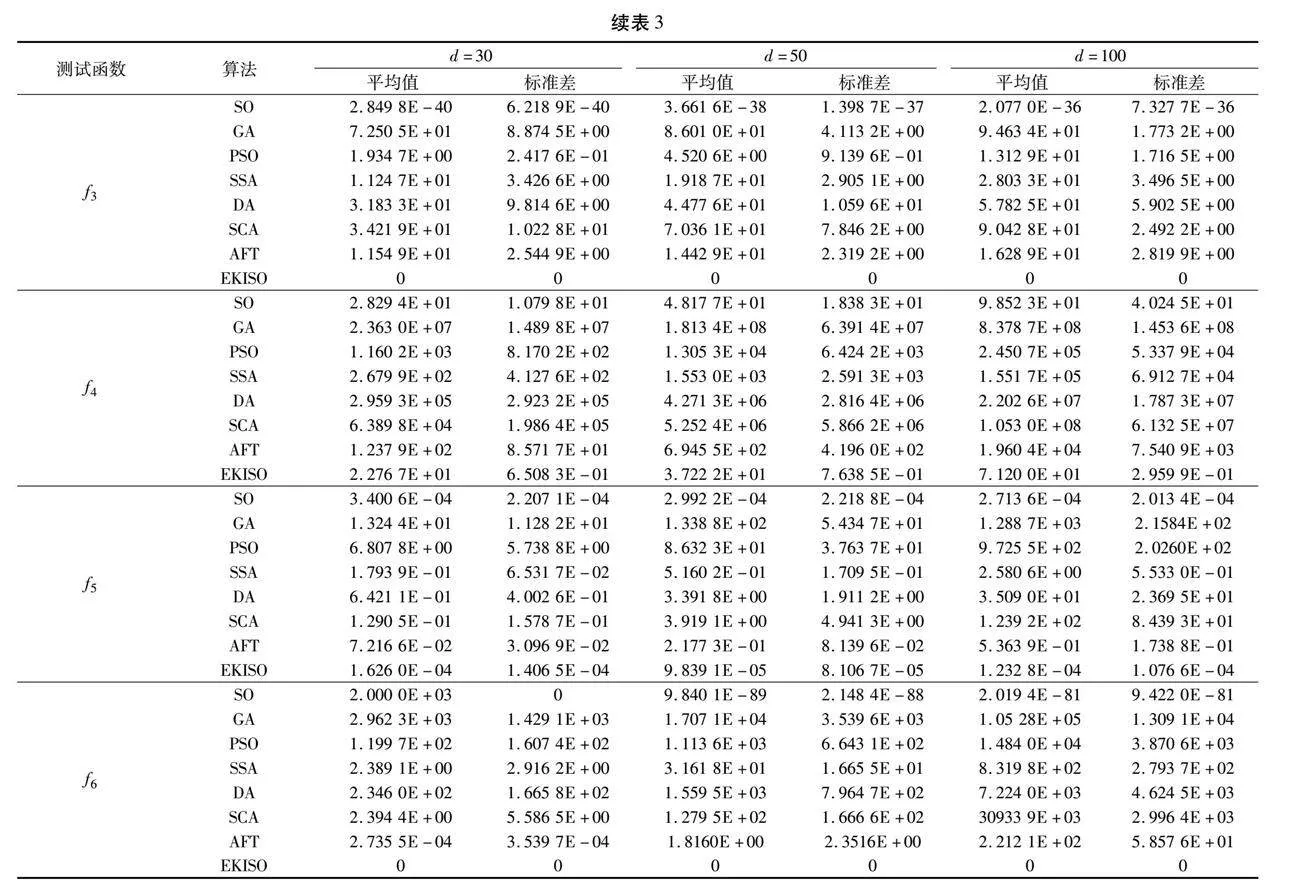
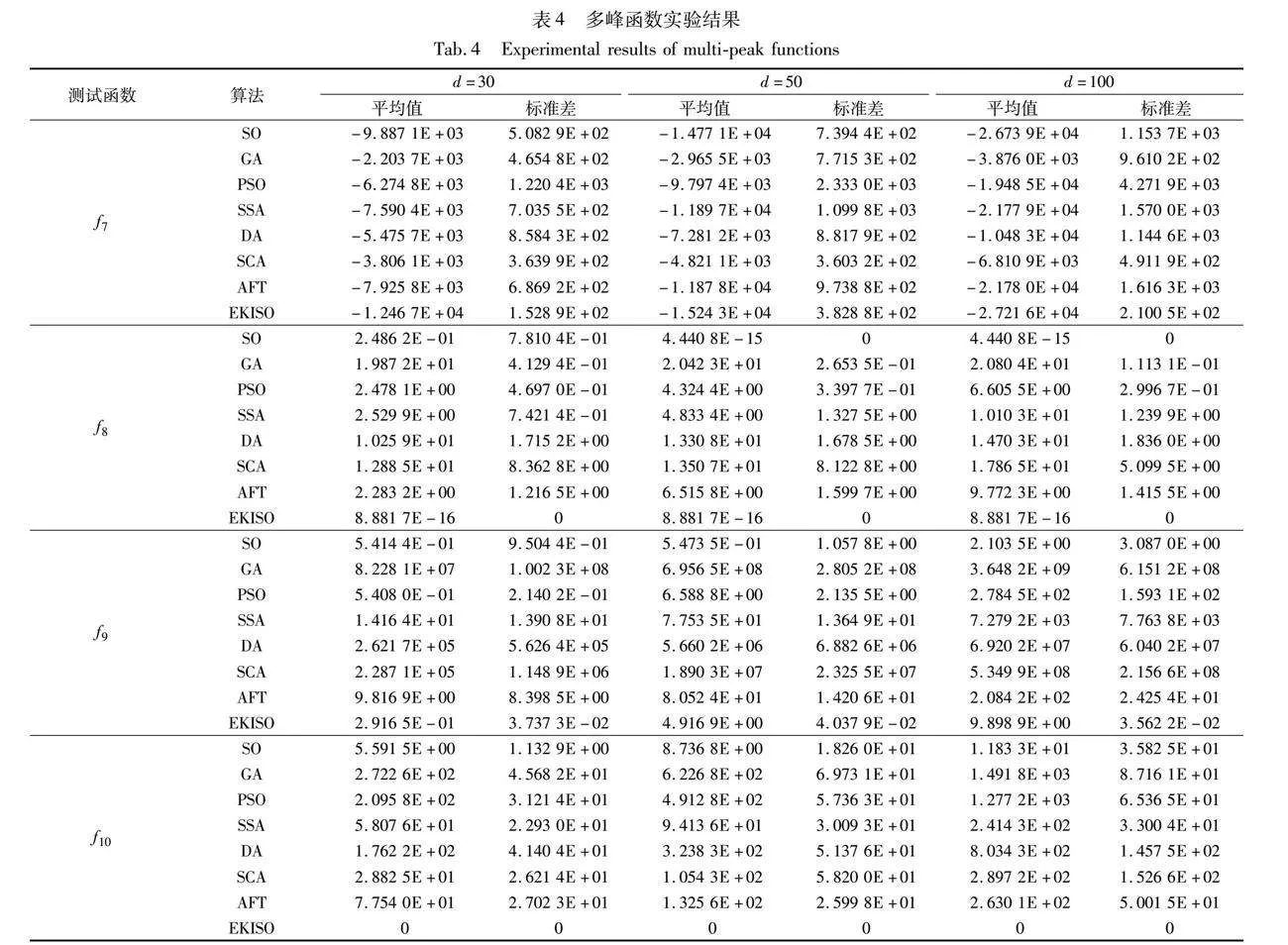
表3～5展示了8种算法在f1～f14上的实验结果。由表3可知，EKISO在6个单峰函数中，平均值和标准差在三种维度上的实验结果均为最优值，表现优于其他算法。由表4可知，EKISO在2个多峰函数中，平均值和标准差在三种维度上的实验结果均优于其他算法。d=30时，EKISO在f7和f9中平均值和标准差均排名第一；d=50时，EKISO在f7中平均值排名第一、标准差排名第二，在f9中平均值排名第二、标准差排名第一；d=100时，EKISO在f7中平均值和标准差均排名第一，在f9中平均值排名第二、标准差排名第一。由表5可知，EKISO在4个固定维函数上，平均值和标准差的实验结果均为所有算法中最优的。

图4展示了部分单峰、多峰和固定维测试函数的收敛曲线图。由图4可以看出，EKISO比其他算法具有更快的收敛速度和更高的收敛精度，相较于SO寻优效果有较大提升，证明了本文改进方法的有效性。

总之，EKISO相比于其他优化算法有更好的寻优能力，在收敛速度和收敛精度方面均有较好的表现。相比于SO，精英初始化提高了初始种群质量、加速了迭代初期的收敛速度，包含振荡因子的螺旋觅食策略使得算法的全局搜索能力更强，K近邻信息共享提高了算法的局部逃逸能力，从而使算法更加靠近最优解。

3.3 CEC2017测试函数结果分析

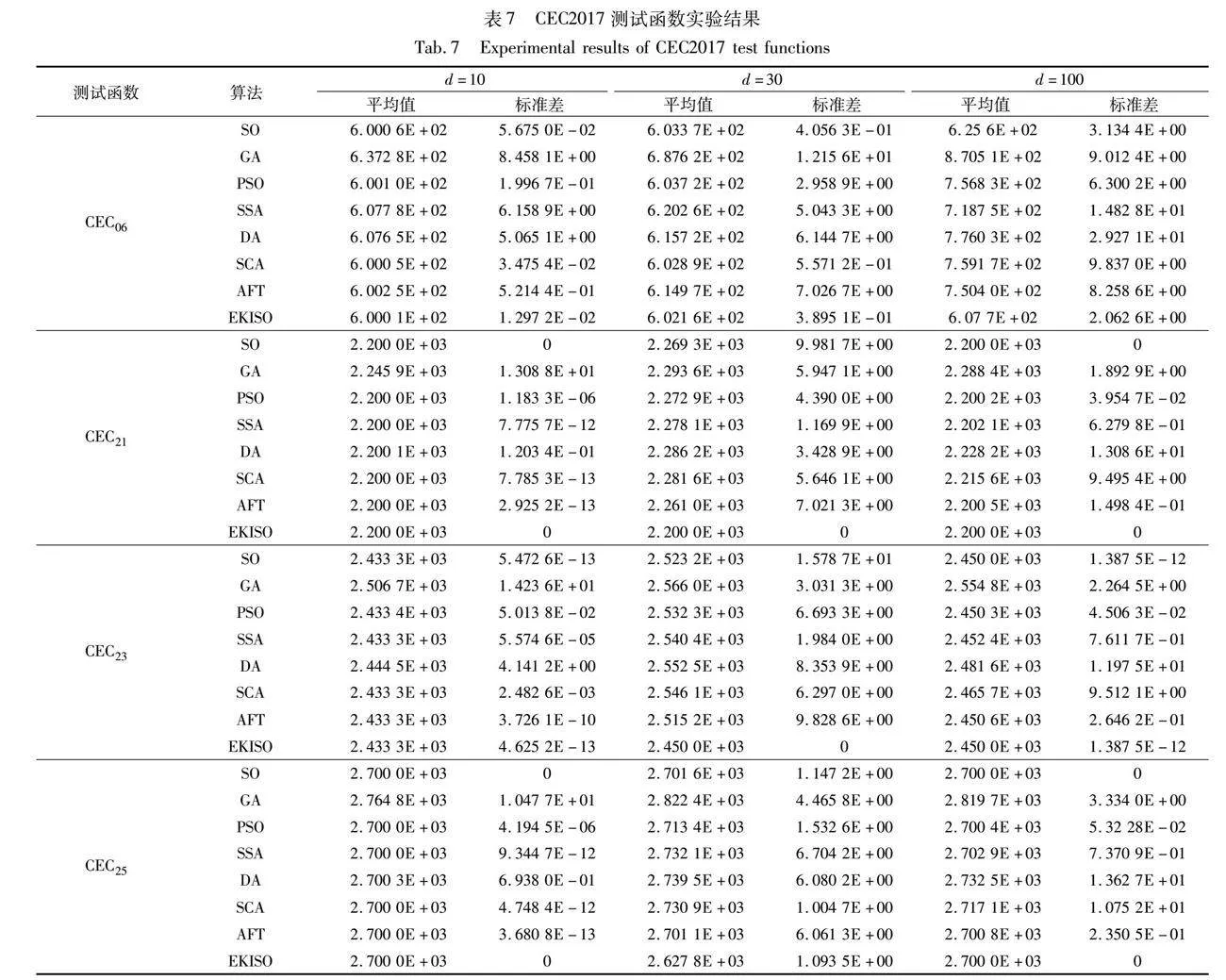
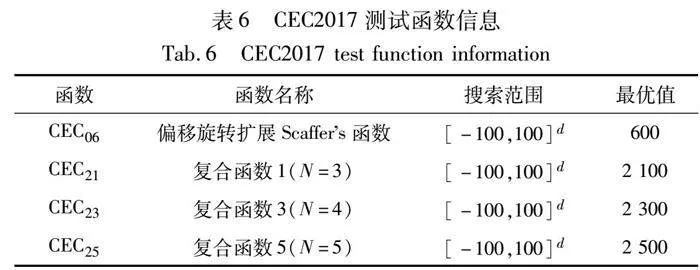
CEC2017测试函数比经典测试函数更加复杂，随着维度增加求解更具有挑战性。本文选取4个CEC2017测试函数进一步评估EKISO的寻优性能。4个CEC2017测试函数详情见表6。

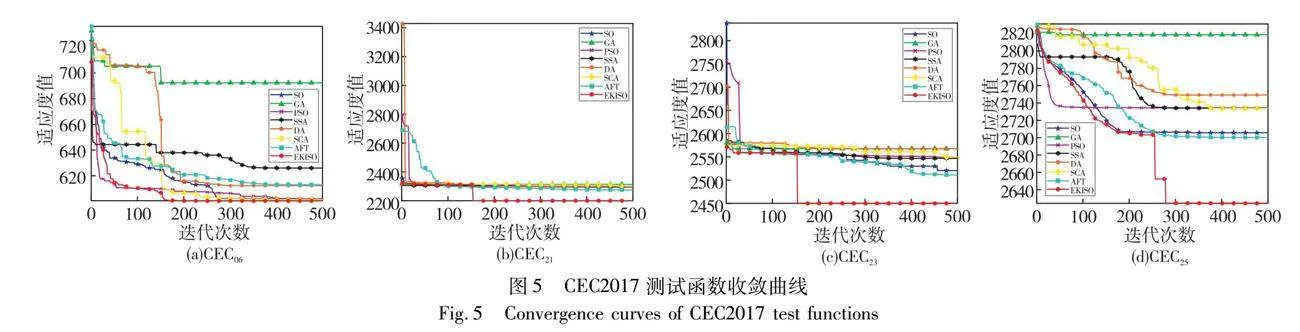
表7展示了8种算法在4个CEC2017测试函数上d=10、30和100时的实验结果。由表7可知，EKISO在每个函数中，平均值和标准差在三种维度上的实验结果均优于其他算法。图5展示了CEC2017测试函数的收敛曲线。由图5可知，EKISO的收敛速度明显优于其他七种算法，且收敛精度最高。

在CEC2017测试函数上的实验结果，体现了EKISO具有良好的寻优性能，证明了改进方法的有效性和实用性。

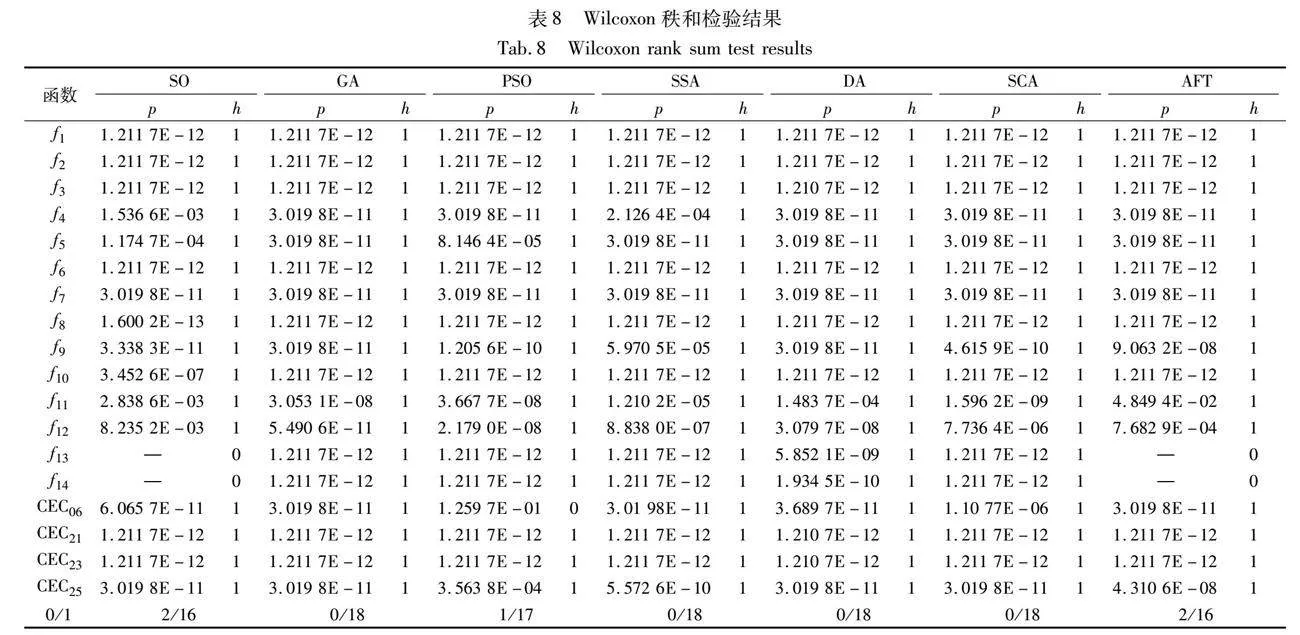
3.4 Wilcoxon秩和检验

为了评估本文算法的性能，表8展示了采用Wilcoxon秩和检验［31］结果，进一步验证EKISO是否与其他算法有显著性差异。当p＜0.05时，说明EKISO与比较算法的差异更显著，“—”表示两种算法效果相差不大，“h=1，h=0”分别表示EKISO优于或差于其他算法。

由表8可知，大部分秩和检验的p值均小于0.05，h值为1，证明EKISO与其他七种对比算法的寻优结果存在显著性差异。

3.5 与其他改进蛇算法的对比分析

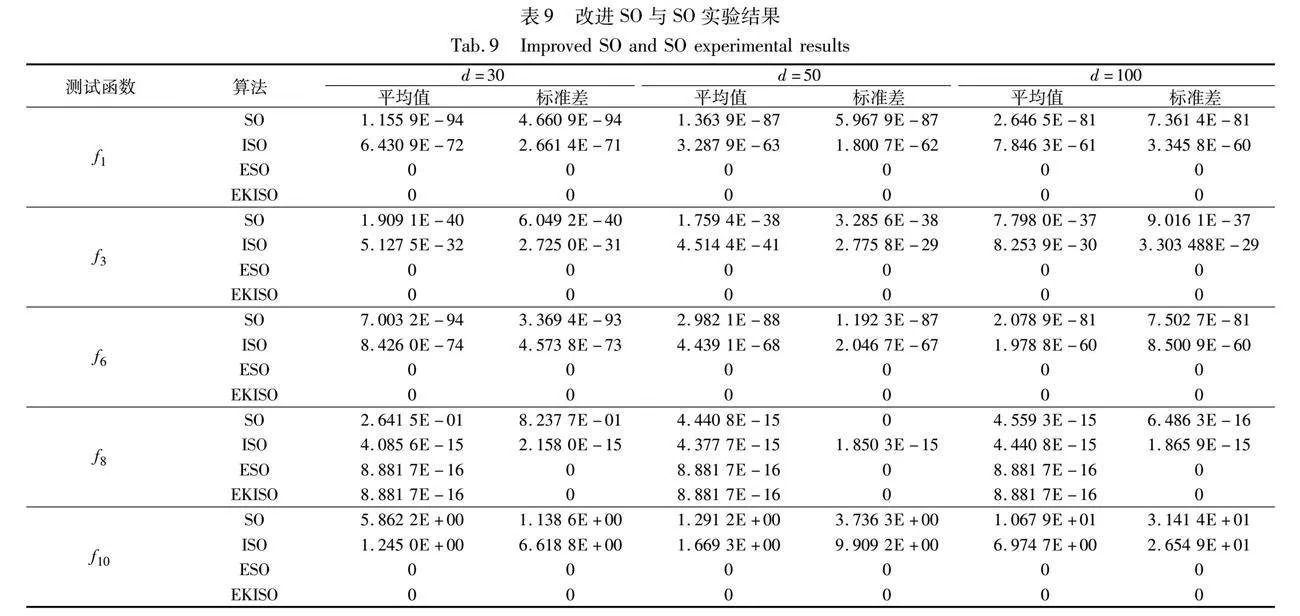
对本文EKISO和ISO［24］、ESO［25］、原始SO［22］的寻优能力进行对比分析，利用表2中的3个单峰测试函数和2个多峰测试函数对SO、ISO、ESO和EKISO算法分别在d=30、50和100时进行测试。为了实验公平性，所有算法相同的参数均保持一致，每个算法在每个测试函数上均独立运行30次，实验结果见表9。

由表9可知，EKISO与ESO寻优性能相当，在每个函数的不同维度上均能寻得理论最优值。而ISO和SO在寻优性能方面表现较为一般，在寻优精度方面还需进一步提高。实验结果证明，本文对于SO的改进使算法的性能显著提升，与同类型改进方法寻优能力不相上下，甚至优于部分改进算法。

3.6 种群初始化精英个体对寻优性能的影响分析

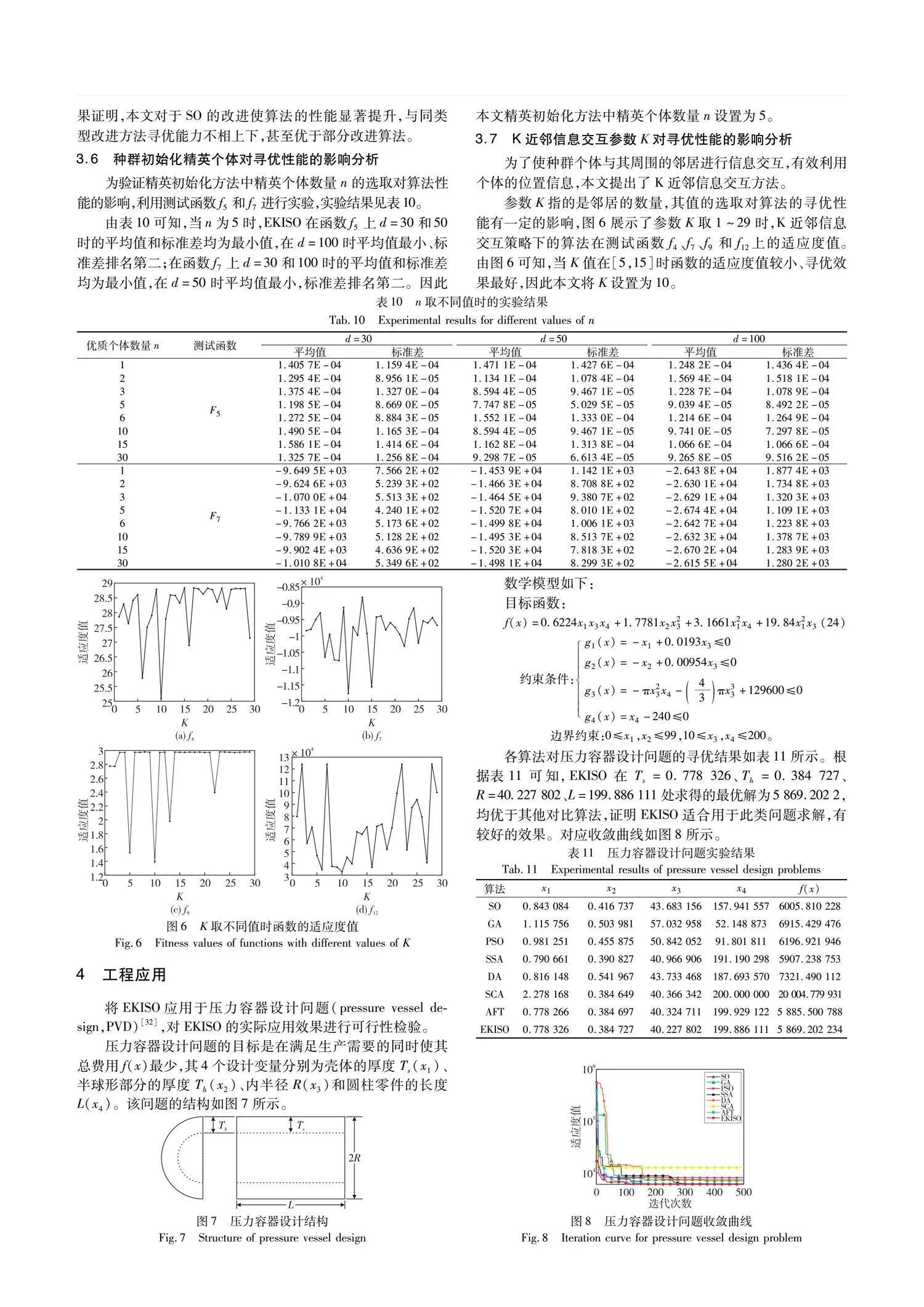
为验证精英初始化方法中精英个体数量n的选取对算法性能的影响，利用测试函数f5和f7进行实验，实验结果见表10。

由表10可知，当n为5时，EKISO在函数f5上d=30和50时的平均值和标准差均为最小值，在d=100时平均值最小、标准差排名第二；在函数f7上d=30和100时的平均值和标准差均为最小值，在d=50时平均值最小，标准差排名第二。因此本文精英初始化方法中精英个体数量n设置为5。

3.7 K近邻信息交互参数K对寻优性能的影响分析

为了使种群个体与其周围的邻居进行信息交互，有效利用个体的位置信息，本文提出了K近邻信息交互方法。

参数K指的是邻居的数量，其值的选取对算法的寻优性能有一定的影响，图6展示了参数K取1～29时，K近邻信息交互策略下的算法在测试函数f4、f7、f9和f12上的适应度值。由图6可知，当K值在［5，15］时函数的适应度值较小、寻优效果最好，因此本文将K设置为10。

4 工程应用

将EKISO应用于压力容器设计问题（pressure vessel design，PVD）［32］，对EKISO的实际应用效果进行可行性检验。

压力容器设计问题的目标是在满足生产需要的同时使其总费用f（x）最少，其4个设计变量分别为壳体的厚度Ts（x1）、半球形部分的厚度Th（x2）、内半径R（x3）和圆柱零件的长度L（x4）。该问题的结构如图7所示。

数学模型如下：

目标函数：

f（x）=0.6224x1x3x4+1.7781x2x23+3.1661x21x4+19.84x21x3（24）

约束条件：g1（x）=-x1+0.0193x3≤0g2（x）=-x2+0.00954x3≤0g3（x）=-πx23x4-43πx33+129600≤0g4（x）=x4-240≤0

边界约束：0≤x1，x2≤99，10≤x3，x4≤200。

各算法对压力容器设计问题的寻优结果如表11所示。根据表11可知，EKISO在Ts=0.778 326、Th=0.384 727、R=40.227 802、L=199.886 111处求得的最优解为5 869.202 2，均优于其他对比算法，证明EKISO适合用于此类问题求解，有较好的效果。对应收敛曲线如图8所示。

5 结束语

针对SO收敛速度较慢、易陷入局部最优的问题，本文结合精英初始化和K近邻提出改进蛇优化算法（EKISO）。通过精英初始化方法，提高了初始种群质量、加速算法收敛；利用包含振荡因子的螺旋觅食策略进行全局勘探阶段的位置更新，有利于蛇优化算法扩大搜索范围并提高局部逃逸能力；结合K近邻思想提出一种新的位置更新机制，增强了种群个体与其周围邻居之间的信息交互能力，加快了收敛速度，提高了收敛精度。在14个经典测试函数和4个CEC2017测试函数上的性能测试，验证了EKISO具有更好的寻优能力、更快的收敛速度和更高的收敛精度。此外，在压力容器设计问题上的应用，证明了EKISO具有实际工程应用价值。虽然EKISO具有一定的优越性，但K近邻信息交互方法中K的取值较为单一，在今后的工作中将研究如何根据目标函数的特点对K值进行自适应取值，以进一步提高EKISO的性能。

参考文献：

［1］Tian Aiqing，Liu Feifei，Lyu Hongxia.Snow geese algorithm：a novel migration-inspired meta-heuristic algorithm for constrained engineering optimization problems［J］.Applied Mathematical Modelling，2024，126：327-347.

［2］Toaza B，Esztergár-Kiss D.A review of metaheuristic algorithms for solving TSP-based scheduling optimization problems［J］.Applied Soft Computing，2023，148：110908.

［3］Dey B，Raj S，Mahapatra S，et al.A variegated GWO algorithm implementation in emerging power systems optimization problems［J］.Engineering Applications of Artificial Intelligence，2023，129：107574.

［4］Gharaei A，Hoseini S A，Karimi M.Modelling and optimal lot-sizing of the replenishments in constrained，multi-product and bi-objective EPQ models with defective products：generalised cross decomposition［J］.International Journal of Systems Science：Operations & Logistics，2020，7（3）：262-274.

［5］Beheshti Z.UTF：upgrade transfer function for binary meta-heuristic algorithms［J］.Applied Soft Computing，2021，106：107346.

［6］Renkavieski C，Parpinelli R S.Meta-heuristic algorithms to truss optimization：literature mapping and application［J］.Expert Systems with Applications，2021，182：115197.

［7］Faramarzi-Oghani S，Dolati N P，Talbi E G，et al.Meta-heuristics for sustainable supply chain management：a review［J］.International Journal of Production Research，2023，61（6）：1979-2009.

［8］Tema E Y，Sahmoud S，Kiraz B.Radar placement optimization based on adaptive multi-objective meta-heuristics［J］.Expert Systems with Applications，2024，239：122568.

［9］Valdez F，Castillo O，Cortes-antonio P，et al.Applications of intelligent optimization algorithms and fuzzy logic systems in aerospace：a review［J］.Applied and Computational Mathematics，2022，21（3）：233-245.

［10］Mishra R，Bajpai M K.A novel multi-agent genetic algorithm for limited- view computed tomography［J］.Expert Systems with Applications，2024，238：122195.

［11］Xiao Zhong，Lu Xinzhu，Ning Jun，et al.COLREGs-compliant unmanned surface vehicles collision avoidance based on improved diffe-rential evolution algorithm［J］.Expert Systems with Applications，2024，237：121499.

［12］Esfandyari M，Delouei A A，Jalai A.Optimization of ultrasonic-excited double-pipe heat exchanger with machine learning and PSO［J］.International Communications in Heat and Mass Transfer，2023，147：106985.

［13］贾鹤鸣，陈丽珍，力尚龙，等.透镜成像反向学习的精英池侏儒猫鼬优化算法［J］.计算机工程与应用，2023，59（24）：131-139.（Jia Heming，Chen Lizhen，Li Shanglong，et al.Optimization algorithm of elite pool dwarf mongoose based on lens imaging reverse learning［J］.Computer Engineering and Applications，2023，59（24）：131-139.）

［14］Lakshmi A V，Mohanaiah P.WOA-TLBO：whale optimization algorithm with teaching-learning-based optimization for global optimization and facial emotion recognition［J］.Applied Soft Computing，2021，110：107623.

［15］Li Yibing，Yang Zipeng，Wang Lei，et al.A hybrid imperialist competitive algorithm for energy-efficient flexible job shop scheduling problem with variable-size sublots［J］.Computers & Industrial Engineering，2022，172：108641.

［16］Muisyo I N，Muriithi C M，Kamau S I.Enhancing low voltage ride through capability of grid connected DFIG based WECS using WCA-PSO tuned STATCOM controller［J］.Heliyon，2022，8（8）：e09999.

［17］Kacha L，Zitouni A，Djoudi M.KAB：a new k-anonymity approach based on black hole algorithm［J］.Journal of King Saud University-Computer and Information Sciences，2022，34（7）：4075-4088.

［18］Zhang Ziyu，Gao Yuelin，Liu Yingchun，et al.A hybrid biogeography-based optimization algorithm to solve high-dimensional optimization problems and real-world engineering problems［J］.Applied Soft Computing，2023，144：110514.

［19］Xia Xuewen，Gui Ling，Zhang Yinglong，et al.A fitness-based adaptive differential evolution algorithm［J］.Information Sciences，2021，549：116-141.

［20］Liu Chao，Wu Lei，Xiao Wensheng，et al.An improved heuristic mecha-nism ant colony optimization algorithm for solving path planning［J］.Knowledge-Based Systems，2023，271：110540.

［21］Ma Yunpeng，Zhang Xinxin，Song Jiancai，et al.A modified teaching-learning-based optimization algorithm for solving optimization problem［J］.Knowledge-Based Systems，2021，212：106599.

［22］Hashim F A，Hussien A G.Snake optimizer：a novel meta-heuristic optimization algorithm［J］.Knowledge-Based Systems，2022，242：108320.

［23］王永贵，赵炀，邹赫宇，等.多策略融合的蛇优化算法及其应用［J］.计算机应用研究，2024，41（1）：134-141.（Wang Yonggui，Zhao Yang，Zou Haoyu，et al.Multi-strategy fusion snake optimizer and its application［J］.Application Research of Computers，2024，41（1）：134-141.）

［24］占宏祥，汪廷华，张昕.一种融合反向学习机制与差分进化策略的蛇优化算法［J/OL］.郑州大学学报：理学版.（2024-01-11）.https：//doi.org/10.13705/j.issn.1671-6841.2023113.（Zhan Hongxiang，Wang Tinghua，Zhang Xin.Snake optimizer algorithm based on opposition-based learning mechanism and differential evolution strategy［J/OL］.Journal of Zhengzhou University：Natural Science Edition.（2024-01-11）.https：//doi.org/10.13705/j.issn.1671-6841.2023113.）

［25］Yao Liguo，Yuan Panliang，Tsai C Y，et al.ESO：an enhanced snake optimizer for real-world engineering problems［J］.Expert Systems with Applications，2023，230：120594.

［26］Zhao Weiguo，Zhang Zhenxing，Wang Liying.Manta ray foraging optimization：an effective bio-inspired optimizer for engineering applications［J］.Engineering Applications of Artificial Intelligence，2020，87：103300.

［4ab0a171c4e84eecdfa31750ba34b7cc27］Tawhid M A，Ibrahim A M.Improved salp swarm algorithm combined with chaos［J］.Mathematics and Computers in Simulation，2022，202：113-148.

［28］Parmaksiz H，Yuzgec U，Dokur E，et al.Mutation based improved dragonfly optimization algorithm for a neuro-fuzzy system in short term wind speed forecasting［J］.Knowledge-Based Systems，2023，268：110472.

［29］Fan Fang，Liu Gaoyuan，Geng Jiarong，et al.Optimization of remote sensing image segmentation by a customized parallel sine cosine algorithm based on the taguchi method［J］.Remote Sensing，2022，14（19）：4875.

［30］Braik M.Enhanced Ali Baba and the forty thieves algorithm for feature selection［J］.Neural Computing and Applications，2023，35（8）：6153-6184.

［31］Dao P B.On Wilcoxon rank sum test for condition monitoring and fault detection of wind turbines［J］.Applied Energy，2022，318：119209.

［32］Houssein E H，Saeed M K，Al-Sayed M M.EWSO：boosting white shark optimizer for solving engineering design and combinatorial problems［J/OL］.Mathematics and Computers in Simulation.（2023-11-20）.https：//doi.org/10.1016/j.matcom.2023.11.019.

收稿日期：2024-01-24

修回日期：2024-03-18

基金项目：国家自然科学基金面上项目（72071084）；河南省教育厅高等学校重点科研项目（22A120008）

作者简介：王丽娟（1966—），女（通信作者），河南周口人，教授，硕导，博士，CCF会员，主要研究方向为大数据、人工智能（wlj@ncwu.edu.cn）；刘姝含（1998—），女，河南郑州人，硕士研究生，主要研究方向为人工智能、机器学习；王剑（1976—），男，湖北武汉人，副教授，硕导，博士，主要研究方向为人工智能、系统工程理论与方法；田亚旗（1997—），男，河南开封人，硕士研究生，主要研究方向为人工智能、机器学习.