非连通空间对象方向关系表达与推理

摘 要：

为了弥补现有的二维空间对象方向关系表达模型大都利用点、最小外包矩形等近似地代替空间对象，距离真实空间对象间方向关系的描述与推理仍存在差距的不足，提出了一种基于Voronoi图的非连通空间对象方向关系表达模型。该模型借助Gestalt心理学理论，通过提取非连通空间对象的特征点、特征链，构建空间对象间的可视区域，生成方向关系Voronoi图，实现了非连通、含洞的参考对象与目标对象间方向关系的表达，该模型较好地顾及了空间对象形状、大小等因素带来的影响，表达精度更高、适用范围更广。为了提高复杂空间对象方向关系复合推理的精度，基于该模型提出了一个非连通对象间主方向关系复合推理算法，该算法借助Tile-union运算和Pr运算，实现了该模型下基本主方向关系的复合推理，降低推理结果的不确定性。分析和验证的结果表明，提出的非连通空间对象方向关系模型及复合推理算法，提高了表达与推理的精度，完善和提高了对复杂空间对象方位关系的分析与处理能力。

关键词：Voronoi图；Gestalt心理学理论；非连通空间对象；主方向关系；复合推理

中图分类号：TP311 文献标志码：A 文章编号：1001-3695（2024）09-013-2655-09

doi：10.19734/j.issn.1001-3695.2024.01.0005

Description and reasoning with direction relation of disconnected spatial objects

Wang Miao1， Dong Xingxing2， Gao Jixun1， 2， Fang Zhenxi3， Tang Hao3， Li Song4

（1.Dept. of Computer Science， Henan University of Engineering， Zhengzhou 451191， China; 2.Dept. of Computer Science， Henan Polytechnic University， Jiaozuo Henan 454000， China; 3.Dept. of Computer Science， Zhongyuan University of Technology， Zhengzhou 451191， China; 4.Dept. of Computer Science， Harbin University of Science & Technology， Harbin 150080， China）

Abstract：

In view of the fact that there is still a certain gap in representing and reasoning with the orientation relation between real objects due that the existing models for representing and reasoning with direction relations use a point and minimum bounding rectangle to approximate the spatial object itself， this paper proposed a new model for dealing with the disconnected spatial objects based on Voronoi diagram. With the help of the theory of Gestalt psychological， the proposed model constructed visual regions between spatial objects by extracting the feature points and feature chains of the disconnected spatial objects to generate the direction Voronoi diagram， which realized the representation of directions between the space objects which were disconnected and contain holes. This model fully considered the influence of the shape， size and other factors of the spatial objects， and had higher expression accuracy and wider applicability. In order to improve the precision of reasoning with cardinal directional relations between complex spatial objects， it proposed an algorithm for composing cardinal direction relations defined by the proposed model， which reduced the uncertainty of the results of composition by means of Tile-union operation and Pr operation. The results of analysis and verification show that the proposed model and algorithm reduce the uncertainty of the reasoning results， improve the accuracy of representation and reasoning， and then enhance the ability to analyze and process the direction relations with complex spatial objects.

Key words：Voronoi diagram; theory of Gestalt psychological; disconnected spatial objects; cardinal directional relations; composition

0 引言

空间方向关系是空间关系的重要组成部分，反映了空间物体间的序关系，例如前侧、后侧、左侧、右侧等，广泛应用于空间智能分析处理、城市管网配置、机器人导航、防灾减灾等诸多领域，日益成为数据建模、制图综合、多媒体设计、图像检索等领域研究的热点和难点问题［1，2］。

空间方向关系的表达与推理是空间方向关系研究领域的核心内容，对于空间数据库领域中的空间检索、空间定位、空间存储等都是非常重要的［3，4］。空间方向关系形式化描述作为空间方向关系领域中的一个基础性内容，为空间方向关系的具体应用奠定了基础［5］。目前空间方向关系的研究大多集中在空间方向关系表达与推理模型和基于模型的推理工作［6，7］，例如空间方向关系的复合推理、反关系推理、一致性检验等。

目前，已有一些二维空间区域对象方向关系表达与推理模型被提出，其中代表性的模型包括锥形模型［8］、基于MBR的方向关系模型［9］、方向关系矩阵模型［10］、基于Voronoi图的方向关系模型［11］等。其中，锥形模型将空间对象抽象为点，描述精度不高；基于MBR的方向关系模型利用空间对象最小外包矩形间的方向关系确定空间对象间的方向关系，在一定程度上考虑了空间对象自身大小与形状带来的影响，但未考虑空间对象相交的情况；方向关系矩阵模型通过延伸参考对象的MBR将整个空间区域划分成九个部分，该模型仅仅描述了参照对象外接矩形外部的方向关系，忽略了空间对象的内部细节；基于Voronoi图的方向关系模型利用空间对象的特征点代替空间对象，考虑了空间对象的自身特性，但上述经典模型均未实现含洞的、非连通的空间对象间方向关系的描述，距离真实物体间的位置关系描述仍存在差距［12，13］。近年来，人们相继提出了一系列改进模型，李朋朋等人［14］在2018年改进了Goyal［10］提出的方向关系相似性计算模型，使方向关系矩阵的应用范围更广，相似性计算的结果更准确，但该模型无法描述空间目标相互缠绕的情形；陈超等人［15］在2021年提出了利用方向Voronoi图模型描述面状群组目标间的方向关系，较好地顾及了群组目标自身形状、大小等因素带来的影响，但无法较好地同时考虑诸多因素带来的影响；王玉竹等人［16］在2022年在模糊数学思路的基础上，给出了考虑各参考目标形状和相对大小的空间方向关系表达模型，更符合人们的方位认知习惯，但并未考虑非连通、含洞的空间对象间的空间方向关系［17］。综上，单目标空间对象方向关系模型大多以规则的、连通的空间对象为研究目标，针对含洞、非连通空间对象的深入研究相对较少，在一定程度上降低了空间方向关系模型的适用性，与真实对象有一定的差距，当前缺乏统一的空间关系模型描述非连通空间对象间的空间方向关系。

目前，已有学者基于点对象、线对象、面对象等对空间方向关系推理问题展开了深入研究，提出了一些推理方法［18～22］。Skiadopoulos等人［23］在2004年采用自然语言描述方向关系矩阵模型，给出了部分定义、定理的形式化描述，并指出现实生活中往往存在非连通的空间对象，但并未给出具体的描述与推理方法。时玉等人［24］在2008年提出了基于真实物体的方向关系模型，但该模型将空间对象抽象为最小外包矩形，仅适用于目标对象是连通的情形，无法体现参考对象的非连通性，并在该模型的基础上，给出了基本主方向关系的复合推理方法，该方法仍依赖手工推理。为处理复杂三维空间对象间的方向关系，刘永山等人［25］在2011年基于单纯形数据模型利用投影方法及区间运算简单的特性，提出三维空间物体方向关系的坐标映射模型，给出了一个该模型下主方向关系网络一致性检验算法。为了避免复杂的手工推理，Wang等人［26］在2022年提出了方向关矩阵模型下基本主方向关系的反关系推理算法，该算法充分发挥了矩阵运算的优势，实现了二维基本主方向关系反关系的自动计算与推理。综上，已有的空间方向关系表达与推理方法大多针对连通区域间的基本主方向关系展开研究，然而现实生活中空间对象往往以非连通的形式存在，现有的空间方向关系研究工作大多针对规则的空间对象，对非连通空间对象间方向关系的表达与推理的研究甚少。

为此，本文建立了基于Voronoi图的非连通空间对象方向关系模型。称之为VG-irregular模型，该模型借助Gestalt心理学理论，将距离相近、特征相似的空间对象的各部分代替整个空间对象，提取特征信息、形成可视区域，构建基于Voronoi图的非连通空间对象方向关系模型，该模型较好地反映了真实空间对象间的方向关系，适用于描述非连通、含洞的空间对象间的方位关系，与已有模型相比，该模型描述精度更高，研究对象更加贴合实际。为了进一步提高空间方向关系的推理精度，基于该模型给出了一个复合推理算法，该算法实现了非连通对象主方向关系的复合推理。推理结果给出了主方向关系中各原子主方向关系所占比例，降低了复合结果的不确定性，理论分析与对比验证的结果表明，该复合推理方法是正确的、完备的。

1 基础知识

Goyal［10］提出的方向关系矩阵模型是描述二维区域空间对象间的方向关系，适用于规则的、连通的以及有连通边界的的封闭单位圆与区域对象。该模型利用参考区域对象的最小外包矩形将空间划分成九个方向区域，如图1所示，通过判断主对象与各方向区域的交叠情况构造一个方向关系矩阵来定义与描述空间对象间的方向关系。方向关系矩阵分为粗略和精确方向关系矩阵，粗略方向关系矩阵的元素值是0或1，记录源目标与参考目标的各方向区域是否相交，如式（1）所示；精确方向关系矩阵的元素值是源目标与各方向区域的交叠面积百分比，如式（2）所示。

真实物体包括同胚的、连通的空间对象和含洞的、不连通的空间对象，这些区域对象的集合记为REG*，例如，图2中源目标对象或参考对象是非连通的空间对象，非连通空间对象具有灵活性、多变性、复杂性等特点，若利用方向关系矩阵模型描述其方向关系，可得图2（a）中目标对象b与参考对象a的方向关系是b E：B a，图2（b）中目标对象b与参考对象a的方向关系是b E a，而实际所感知的图2（a）的方向关系是b E：SE：N：NE a，实际所感知的图2（b）的方向关系是b E：NE a，可见方向关系矩阵模型的描述结果将与真实情况存在较大偏差、精度较低，无法准确描述非连通空间对象间的方向关系。

2 基于Voronoi图的非连通空间对象方向关系表达模型

现有的方向关系模型大多利用点、最小外包矩形等近似地代替空间对象，未考虑非连通空间对象的自身特征，本文提出了一种基于Voronoi图的非连通空间对象方向关系表达模型，用于解决含洞的、非连通的空间对象的建模问题。非连通空间对象间的方向关系是一个整体相对于另一个整体的方向关系，该模型利用非连通空间对象特征链间的方向关系来描述整体空间对象间的方向关系。其主要思想是借助Gestalt心理学理论，将距离相近、特征相似的空间对象的各部分代替整个空间对象，提取空间对象具有代表性的特征点、形成特征链、构建空间对象间的可视区域、生成方向关系Voronoi图、计算Voronoi图各线段的方位角，得到非连通空间对象方向关系模型，其中，特征链在空间方向关系判断的过程中代表着其对应的整个空间对象。

定义12 空间对象特征点是指能够表示空间对象基本结构的点。点目标对象的特征点是点；线目标对象的特征点是起点、中点、终点；面目标对象的特征点是其多边形可视区域的顶点。若空间对象有m、n个特征点，次序可记为p1，p2，p3，…，pm、q1，q2，q3，…，qn。

定义13 空间对象特征链是由两个空间对象间相邻近的一侧的特征点自然而然连接成的曲线，特征链代替空间对象本身，空间对象a的特征链记为Ca。

定义14 可视区域是两个空间对象的特征链邻近的两端连接形成的区域，可视区域可看作是三角形的集合，即每个三角形必须包含两个目标对象的特征点。大多数情况下，可视区域整体是多边形，特殊情况下是一条线段，空间对象a、b可视区域记为Fab。

构造基于Voronoi图的非连通空间对象方向关系表达模型需要经历以下四个阶段：

a）提取特征点，针对空间对象间相邻的一侧，利用格雷厄姆算法求解特征链，夹角序列算法计算特征链直径，借助偏角衡量空间对象综合的幅度。若空间对象特征链边界上的特征点的偏角小于45°，则舍弃该特征点，保留其余特征点，利用提取的全部特征点代替空间对象本身，并且应保证提取空间对象特征点前后的空间关系保持不变。

b）连接特征点形成特征链，构造空间对象间的可视区域，根据Gestalt心理学将空间对象间相邻近的一侧的特征点自然而然连接成曲线，即代替空间对象本身的特征链。然后将两条特征链首首连接、尾尾连接形成由多个三角形构成的多边形可视区域，其中每个三角形的三个顶点中必须既有非连通参考对象的特征点，又有非连通源目标对象的特征点。

c）生成Voronoi图，在空间对象间的多边形可视区域的基础上，依据各个三角形底角的度数范围不同，将三角形分为三种，即底角都是锐角、一个底角是直角、一个底角是钝角。方向关系Voronoi图的连接点由第一、二种三角形腰的中点、第三种三角形一腰中点的垂线和另一腰的中位线、两相邻目标公共边界的起讫点和共点相邻时的公共点组成，将连接点依次连接得到方向关系Voronoi图。

d）计算Voronoi图各线段所对应射线的方位角，将方位角信息转换为空间对象间的方向关系。计算射线方位角之前需要计算源目标对象与参考对象的方向关系Voronoi图的方位角。若源目标对象在参考对象的上、右、右上、左上，则求解Voronoi图各线段的方位角时，以线段的左端点、上端点、左上端点、左下端点为基点，计算各线段对应的方位角。若源目标对象在参考对象的下、左、左下、右下，则求解Voronoi图各线段的方位角时，以线段的右端点、下端点、右下端点、右上端点为基点，计算各线段对应的方位角。

射线方位角是指垂直于Voronoi图各线段、由参考对象指向源目标对象的射线的方位角，得到Voronoi图各线段所对应的射线方位角信息后，将射线方位角信息与空间方向关系对应起来。计算射线方位角方法如下，假设方向关系Voronoi图的线段是EF，E点记为（x1，y1），F点记为（x2，y2），E、F两点的方位角记为βEF，其对应射线方位角β的计算分为两种情况。若x1≠x2，则当β≥0时β=βEF-90°、当β＜0时，β=βEF-90°+360°；若x1=x2，源目标在参考目标的右侧，则β=90°，反之，β=270°。

每个空间方向关系对应一个射线方位角的划分区间，利用八方向描述方法将射线的方位角与空间方向关系对应起来，北 （337.5°，22.5°］、东北（22.5°，67.5°］、东 （67.5°，112.5°］、东南 （112.5°，157.5°］、南 （157.5°，202.5°］、西南（202.5°，247.5°］、西 （247.5°，292.5°］、西北 （292.5°，337.5°］，由此可得空间对象间的方向关系，该模型同样适用于参考对象和源目标对象均为非连通空间对象的情况。

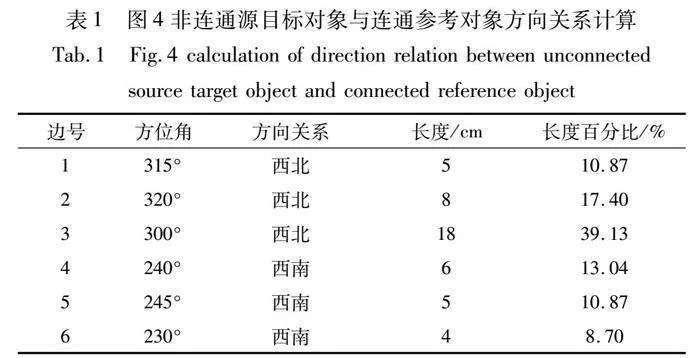
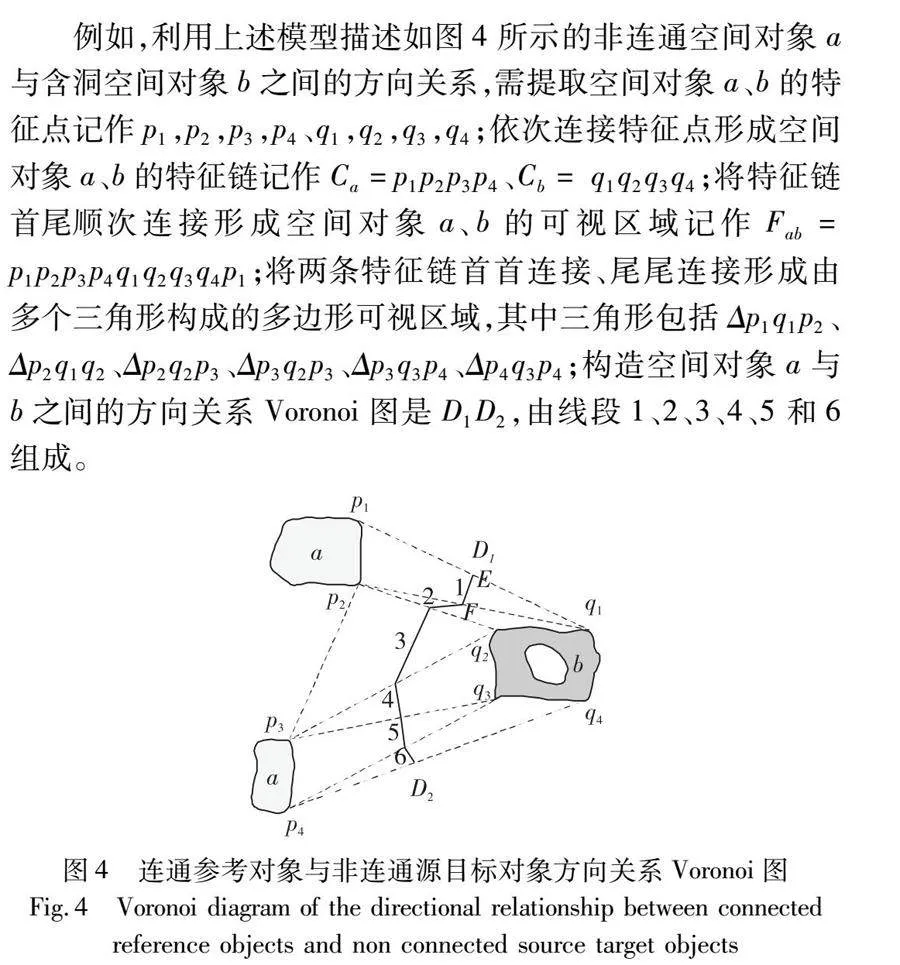
例如，利用上述模型描述如图4所示的非连通空间对象a与含洞空间对象b之间的方向关系，需提取空间对象a、b的特征点记作p1，p2，p3，p4，q1，q2，q3，q4；依次连接特征点形成空间对象a、b的特征链记作Ca=p1p2p3p4、Cb= q1q2q3q4；将特征链首尾顺次连接形成空间对象a、b的可视区域记作Fab= p1p2p3p4q1q2q3q4p1；将两条特征链首首连接、尾尾连接形成由多个三角形构成的多边形可视区域，其中三角形包括Δp1q1p2、Δp2q1q2、Δp2q2p3、Δp3q2p3、Δp3q3p4、Δp4q3p4；构造空间对象a与空间对象b之间的方向关系Voronoi图是D1D2，由线段1、2、3、4、5和6组成。

按照上述计算Voronoi图各线段所对应射线方位角的方法，分别计算出各线段所对应的方位角、方向关系、线段长度以及长度百分比，如表1所示，经计算可得非连通源目标对象a的67.4%在参考对象b的西北方向，32.6%在参考对象b的西南方向。

综上所述，利用本文提出的VG-irregular模型描述非连通空间对象间的方向关系时大致经历四个过程，即：a）提取非连通空间对象特征点；b）借助Gestalt心理学理论，将距离相近、特征相似的空间对象特征点连接形成特征链，通过特征链构造可视区域；c）在上述过程的基础上生成方向关系Voronoi图；d）计算Voronoi图中各线段的方位角，并利用射线方位角信息与空间方向关系的对应关系得到非连通空间对象间的方向关系。

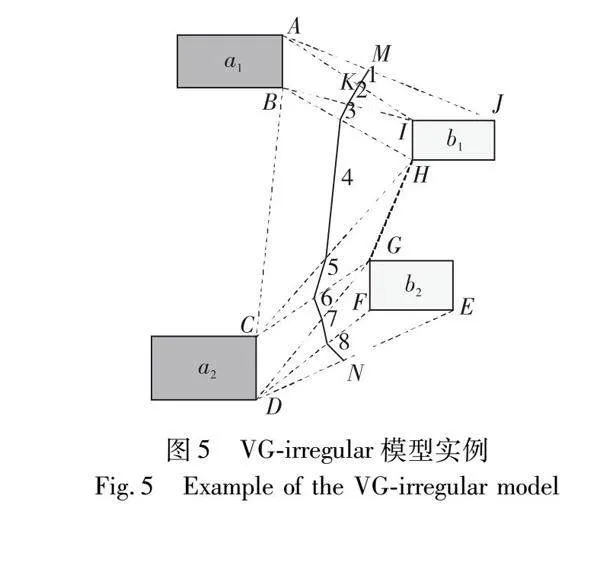
下面将通过一个具体的实例说明VG-irregular模型的表示方法及过程，如图5所示。

a）利用非连通目标对象a1、a2和非连通参考对象b1、b2特征链边界上的特征点的偏角信息，提取非连通空间对象a、b的特征点，即特征点A、B、C、D、E、F、G、H、I、J。

b）连接空间对象a1、a2、b1、b2特征点，构建空间对象a、b的特征链，即特征链ABCD、EFGHIJ。然后将特征链ABCD和特征链EFGHIJ首首连接、尾尾连接形成由多个三角形构成的多边形可视区域，即可视区域ABCDEFGHIJA。其中三角形包括△AIJ、△ABI、△BHI、△BCH、△CHG、△CDG、△DEF。

c）判断各三角形的类型（锐角三角形、直角三角形、钝角三角形），连接各三角形的中点或者垂点。△AIJ是钝角三角形，则取AI的中点作垂线得到线段MK，同理可得，线段1、2、3、4、5、6、7、8。将空间对象a、b的起讫点M、N和8条线段依次连接得到空间对象a、b的方向关系Voronoi图，即折线MN。

d）计算8条线段的方位角，根据方位角与空间方向关系对应得到每条线段对应的方向关系，例如线段1：45°—90°＋360°＝315°，对应西北方向，其余同理，并计算出各线段所线段长度和长度百分比，具体如表2所示。

经计算可得图5中的非连通源目标对象a的81.25%在参考对象b的西北方向，6.25%在参考对象b的西方向，12.5%在参考对象b的西南方向。可见VG-irregular模型较好地反映了真实空间对象间的方向关系，适用于描述非连通、含洞的空间对象间的方位关系，该模型描述精度更高，研究对象更加贴合实际。

3 非连通空间对象间主方向关系的复合推理

为了复合推理的精度，降低复合推理结果的不确定性，在VG-irregular方向关系模型的基础上，对空间方向关系的推理进行研究，提出了一个非连通对象间主方向关系复合推理算法。根据本文模型所得空间对象间含比例大小的方向关系，将其转换为方位角形式，用θ表示；具体的划分方法是北：θ1=（337.5°，22.5°］、东北：θ2=（22.5°，67.5°］、东：θ3=（67.5°，112.5°］、东南：θ4=（112.5°，157.5°］、南：θ5=（157.5°，202.5°］、西南：θ6=（202.5°，247.5°］、西：θ7=（247.5°，292.5°］、西北：θ8=（292.5°，337.5°］。基于Skiadopoulos和Koubarakis提出的原子主方向关系合成表进行改进，得到如表3所示的以“方位角”形式展示的原子主方向关系复合表。

若存在空间对象a，b，c∈REG*，满足a θ1 b、b θ2 c，则θ1θ2∈2D*。将利用如式（8）所示的矩阵描述，元素值是0或1，仅仅记录源目标对象与参考对象的方向关系，若源目标对象a在参考对象b的西北方向和西南方向，所对应的矩阵如式（9）所示。

Dir（a，b）=

NW（292.5°，337.5°］N（337.5°，22.5°］NE（22.5°，67.5°］

W（247.5°，292.5°］θ0E（67.5°，112.5°］

SW（202.5°，247.5°］S（157.5，202.5°］SE（112.5°，157.5°］（8）

Dir（a，b）=100000100（9）

定义15 若θ1，…，θk是原子主方向关系，Pr（θ1：…：θk）表示各原子主方向关系θ1、…、θk百分制下所占比例的计算，计算结果满足θ1比例＋：…：＋θk比例=1。

例如：θ4（70%）：θ5（40%），则Pr（θ4（70%）：θ5（40%））=θ4（70%/（70%+40%））：θ5（40%/（70%+40%））=θ4（63.64%）：θ5（36.36%）。

引理1［18］ 若θ1是原子主方向关系，θ2是主方向关系，则满足θ1θ2=θ1Most（θ1，Br（θ2））。

定理1 若θ1、θ2是主方向关系，θ1=θ11：…：θ1k，θ2=θ21：…：θ2m，θ11，…，θ1k是原子主方向关系，则满足θ1kθ2=Pr（θ1kMost（θ1k，Br（θ2）））。

证明 已知k=1，即θ1=θ11，θ1是原子主方向关系，θ2、θ3是主方向关系，若a θ1（100%） b，b θ21（x%）：θ22（1-x%）c，根据引理1可知，存在θ3∈{θ1θ21：θ22}，根据定义15可知，对于任意复合结果θ31（m%）：θ32（n%），存在θ31（m%）：θ32（n%）=θ31（m%/（m%+n%））：θ32（n%/（m%+n%），故命题成立。证毕。

引理2［18］ 若θ1、θ2是基本主方向关系，θ1=θ11：…：θ1k，θ2=θ21：…：θ2m，则满足θ1θ2 ={ Q∈D： （s1，…， sk）（Q=Tile-union（s1，…， sk）∧s1∈θ11θ2∧…∧sk∈θ1kθ2）}。

定理2 若θ1、θ2是主方向关系，θ1=θ11：…：θ1k，θ2=θ21：…：θ2m，则满足θ1θ2 =Pr（Tile-union（s1，…，sk︱s1∈θ11θ2，…， sk∈θ1kθ2））。

证明 假设k=1，则θ1=θ11，θ1是原子主方向关系， 其结论显然成立；假设k>1，令Q∈θ1θ2，则根据定义6，存在物体a、b、c∈REG*，满足a θ1 b∧b θ2 c∧a Q c。已知a θ1 b成立，则存在物体 a1，…，ak∈REG*，a=a1∪…∪ak，使a1θ11b∧…∧ak θ1k b成立，故（a1θ11b∧…∧ak θ1k b）∧b θ2 c∧a Q c。既然a=a1∪…∪ak与a Q c成立，则存在主方向关系Q1，…，Qk，使得Q=Tile-union（Q1，…，Qk），a1 Q1 c∧…∧ak Qk c成立，故（a1θ11b∧…∧ak θ1k b）∧b θ2 c∧（a1 Q1 c∧…∧ak Qk c）。类似地，（a1 θ11 b∧b θ2 c∧a1 Q1 c）∧…∧ （akθ1k b∧b θ2 c∧ak Qk c）成立，因此Q1∈θ11θ2，…， Qk∈θ1kθ2，即Q=Tile-union （Q1，…， Qk） 成立，根据定理1可知，θ1θ2 =Pr（Tile-union （Q1，…， Qk））成立，故命题成立。证毕。

对于任意两个主方向关系的复合，首先根据引理1和定理1计算出一个主方向关系中各原子主方向关系与另一个主方向关系的复合，利用引理2和定理2对上述复合结果进行Tile-union运算和Pr运算，该复合结果给出了主方向关系中各原子主方向关系所占比例。基于上述方法，给出了一个非连通对象间主方向关系复合推理算法COM_PR（），该复合算法如下。

算法 COM_PR（θ）

输入：两个基本主方向关系θ1∈D*、θ2∈D*，其中θ1=θ11：…：θ1k，θ2=θ21：…：θ2k，θ11，…，θ2k是原子主方向关系。

输出：θ1与θ2的合成结果θ3。

begin //计算Sij

ElemType S，S1i; //定义S、S1i变量

for int i：=1 to k do

for int j：=1 to k do //依次计算θ1i与θ2的复合关系

S=θ1iθ2; //依据定理1即可实现

S1i：=S1i∪S; //依次合并得到初步的复合结果

//对S1i中的元素进行Tile-union运算

ElemType S0; //定义S0变量

if （S！=NULL） then //对S进行判空操作

S0=S11; /*将临时变量的值，赋给S0，以便S0与下一个集合运算*/

for int i：=1 to k-1 do

S0=Tile-union（S0，S1i+1）∪S0; //依据定理2即可实现

//对θ3k中的方向关系进行比例运算

if（S！=NULL） then //对S进行判空操作

for int i：=1 to S0.length do

θ3=θ3∪{Pr（S0i）}; //依次对θ3中的方向关系进行Pr运算

return θ3;

end

定理3 主方向关系复合算法COM_PR（）是正确的、完备的。

证明 若θ1∈D*、θ2∈D*，则存在θ3∈D*。定理1给出了θ1i与θ2的复合关系Sij∈θ1iθ2j（1≤i≤k，1≤j≤k，1≤i≤length（Si），1≤j≤length（Sj）），其正确性在相应的定理中给出了证明。定理2实现了Tile-union运算和Pr运算，即S1和S2中的元素依次进行Tile-union运算，其结果放入S0中，运算结束后将S0值赋给S2，然后对S2和S3进行Tile-union运算，依此类推，直到完成对Sk-1和Sk中各元素的Tile-union运算，最后对θ31，…，θ3k进行比例运算，运算结束后赋值给θ3将得到θ1和θ2的复合关系θ3，其正确性和完备性在上述定理中均已证明。故算法COM_PR（）是正确的、完备的。证毕。

综上所述，本文提出的非连通对象间主方向关系复合推理算法COM_PR（）大致经历三个过程，即：a）利用引理1、定理1实现原子主方向关系与主方向关系的复合；b）利用引理2、定理2对上述初步复合结果依次进行Tile-union运算；c）完成Pr运算，实现任意两个主方向关系的复合，并且复合结果给出了主方向关系中各原子主方向关系所占比例。

下面将通过一个具体的实例说明非连通对象间主方向关系复合推理算法的表示方法及过程。已知a NW（30%）：SW（70%） b、b W（40%）：S（60%） c，计算a与c间的方向关系。

a）计算各原子主方向关系与非连通主方向关系的复合。将NW（30%）：SW（70%）W（40%）：S（60%）转换为方位角形式的空间方向关系，即（292.5°， 337.5°］（30%）：（202.5°， 247.5°］（70%）（247.5°， 292.5°］（40%）：（157.5°， 202.5°］（60%），然后计算（292.5°， 337.5°］（247.5°， 292.5°］：（157.5°，202.5°］、（202.5°， 247.5°］（247.5°， 292.5°］：（157.5°， 202.5°］的合成结果，得到S1={（292.5°， 337.5°］，（247.5°， 292.5°］，（292.5°， 337.5°］：（247.5°，292.5°］}、S2={（202.5°，247.5°］}。

b）完成Tile-union运算。针对S1={（292.5°，337.5°］，（247.5°，292.5°］，（292.5°，337.5°］：（247.5°，292.5°］}、S2={（202.5°，247.5°］} 依次进行Tile-union运算。Tile-union（S1，S2）={ （202.5°， 247.5°］：（292.5°， 337.5°］，（202.5°，247.5°］：（247.5°， 292.5°］，（202.5°， 247.5°］：（292.5°， 337.5°］： （247.5°， 292.5°］}。

c）完成Pr运算。针对{（202.5°，247.5°］：（292.5°，337.5°］，（202.5°，247.5°］：（247.5°，292.5°］，（202.5°，247.5°］：（292.5°，337.5°］： （247.5°，292.5°］}进行Pr运算。根据原子主方向关系的比例关系进行基本主方向关系的比例运算，已知空间方向关系（202.5°，247.5°］占比70%、（292.5°，337.5°］占比30%、（247.5°，292.5°］占比40%、（157.5°，202.5°］占比60%， （202.5°，247.5°］：（292.5°，337.5°］的比例关系是（202.5°，247.5°］（70%）：（292.5°，337.5°］（30%），其余同理。可得（202.5°，247.5°］ （70%）：（292.5°，337.5°］ （30%）（202.5°，247.5°］ （63.64%）：（247.5°，292.5°］ （36.36%）、（202.5°，247.5°］ （50%）：（292.5°，337.5°］ （21.43%）：（247.5°，292.5°］ （28.57%）。

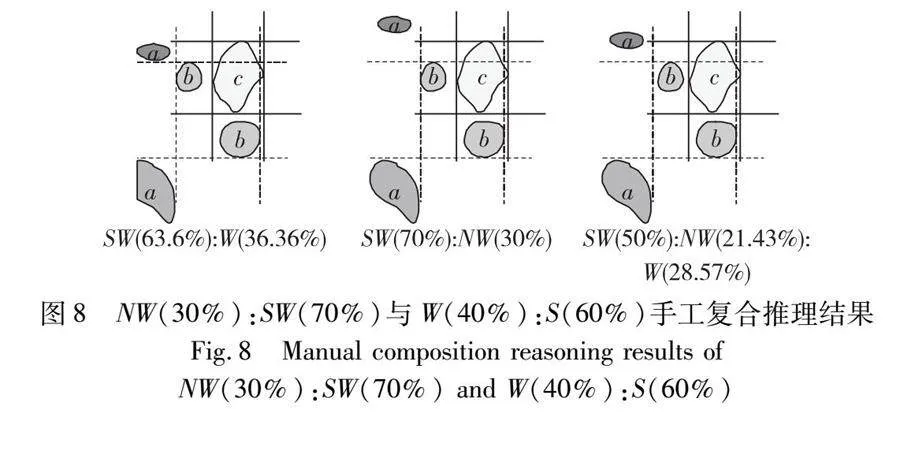
将角度形式的空间方向关系转换为SW（70%）：NW（30%）、SW（63.64%）：W（36.36%）、SW（50%）：NW（21.43%）：W（28.57%）。因此，NW（30%）：SW（70%）与W（40%）：S（60%）复合的结果包括SW（70%）：NW（30%）、SW（63.64%）：W（36.36%）、SW（50%）：NW（21.43%）：W（28.57%） 三种情况，其中SW（70%）：NW（30%）表示空间对象a的70%的部分位于空间对象c的西南方向、空间对象a的30%的部分位于空间对象c的西北方向，另外两种结果的含义同样如此。

4 分析验证

4.1 VG-irregular模型的实例分析与对比

4.1.1 表达精度分析验证

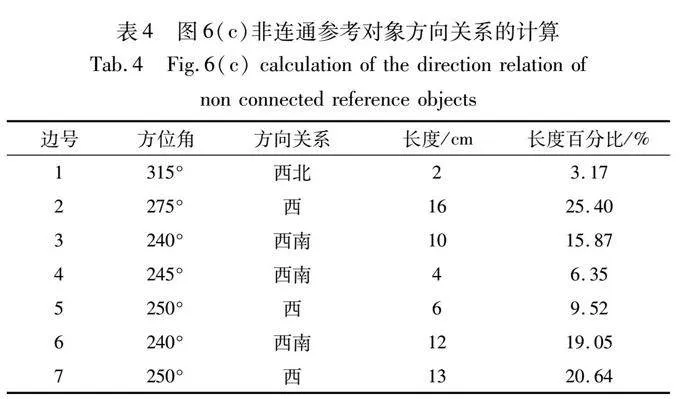
描述如图6（a）所示的非连通空间对象间的方向关系时，利用方向关系矩阵模型得到的空间方向关系是非连通源目标对象a在非连通参考对象b的西、西北方向，如图6（b）所示。若利用VG-irregular方向关系模型描述非连通空间对象间的方向关系，通过提取空间对象特征点、形成特征链、构造可视区域、生成Voronoi图等过程，得到非连通源目标对象a与非连通参考对象b之间的方向关系，如图6（c）所示，即非连通源目标对象a的3.17%在非连通参考对象b的西北方向，a的55.56%在b的正西方向，a的41.27%在b的西南方向，具体计算过程如表4所示。由此可见，VG-irregular模型精度更高，给出了具体的百分比，更加符合现实生活中人们对于方向关系的认识习惯。

4.1.2 空间对象自身特性影响程度分析

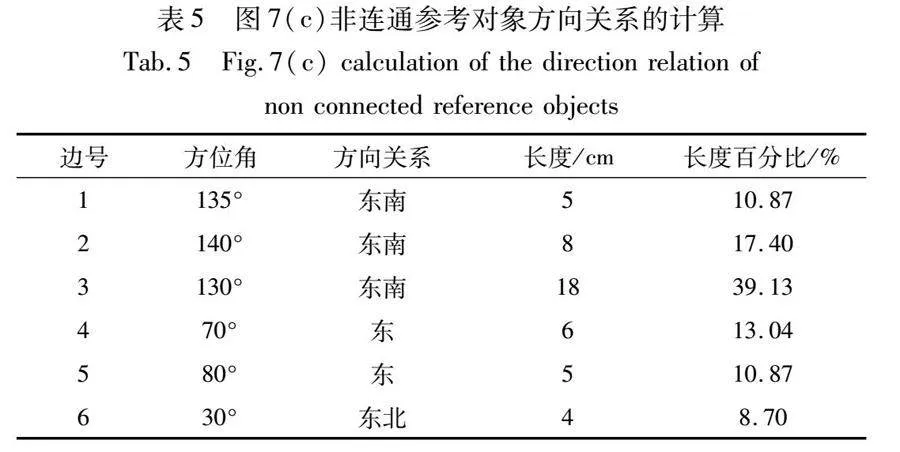
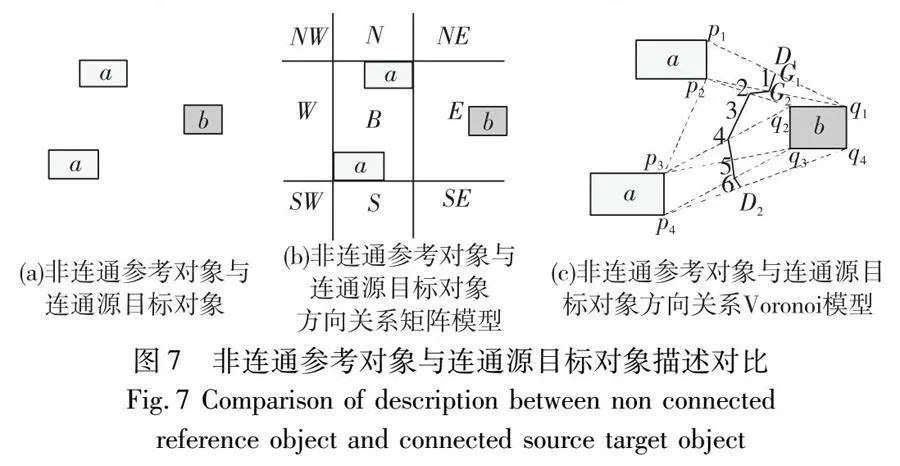
描述如图7（a）所示的非连通参考对象与连通源目标对象间的方向关系时，方向关系矩阵模型将非连通参考对象看作一个整体，可得连通源目标对象b在非连通参考对象a的正西方向，如图7（b）所示，未体现参考对象的非连通特性。若利用本文VG-irregular方向关系模型描述非连通参考对象与连通源目标对象间方向关系，如图7（c）所示，以点G1为基点，可得源目标对象b的64.7%在非连通参考对象a的东南方向，b的23.91%在a的东面，b的11.39%在a的东北方向，具体计算过程如表5所示。从现实角度分析，仅说明空间对象b在空间对象a的正西方向是不正确的，方向关系矩阵模型的描述结果误差较大，而本文VG-irregular方向关系模型的描述结果考虑了空间对象a的非连通性，受空间对象自身特性影响较小。

4.1.3 外在因素影响程度分析

除了上述空间对象自身特性包括形状、大小等因素会影响空间对象间的方向关系，空间对象间的空间距离、简单拓扑关系、分布密度、分布范围等因素也将影响空间方向关系的描述。方向关系矩阵模型利用参考对象的最小外包矩形代替空间对象本身，将空间划分成九个方向区域，忽略了空间距离、简单拓扑关系、分布密度、分布范围等外在因素带来的影响。本文提出的VG-irregular方向关系模型利用方向关系Voronoi图从定性与定量两个角度对非连通空间对象间的空间方向关系进行描述与计算，既顾及了空间对象的大小、形状和距离等因素的影响，又可以获得较为精确的计算结果，适用于多种情况下空间方向关系的描述，在广泛性、正确性、唯一性、普遍性方面均有优势。

综上，无论是描述准确性、受空间对象自身特性影响程度，还是外在因素影响程度，VG-irregular方向关系模型具有明显优势，描述精度更高，适用范围更广，考虑了空间对象形状、大小等因素带来的影响，受空间对象自身特性影响程度较小，所得空间方向关系描述结果更符合现实生活中人们的认知习惯，较好地反映了真实空间对象的形状与空间对象间的方向关系。

4.2 复合算法的实例分析与对比

利用C语言编程实现了算法COM_PR（），在Visual Studio 2019平台上运行，程序实现的基本思路利用引理1、定理1实现原子主方向关系与主方向关系的复合，利用引理2、定理2对上述初步复合结果依次进行Tile-union运算和Pr运算，实现任意两个主方向关系的复合，复合结果给出了主方向关系中各原子主方向关系所占比例。在本节中，将利用两个实例对算法COM_PR（）进行分析验证。通过第一个实例分析验证算法对于非连通主方向关系复合的计算与推理能力，并且与手工推理的结果进行对比；通过第二个实例分析验证算法复合结果的精度，并将其复合结果与具有代表性的Skiadopoulos等人［23］提出的经典推理方法和当前较新的欧阳继红等人［18］提出的主方向关系复合推理方法进行对比分析验证。

下面通过第3章中的实例验证算法COM_PR（）的正确性，即 NW（30%）：SW（70%）W（40%）：S（60%），将空间方向关系转换为方位角形式的空间方向关系，即（292.5°， 337.5°］（30%）：（202.5°，247.5°］（70%）（247.5°，292.5°］（40%）：（157.5°， 202.5°］（60%），利用算法中的前两个for循环计算（292.5°， 337.5°］（247.5°，292.5°］：（157.5°，202.5°］、（202.5°，247.5°］（247.5°， 292.5°］：（157.5°， 202.5°］，得到S1={（292.5°， 337.5°］，（247.5°， 292.5°］，（292.5°， 337.5°］： （247.5°，292.5°］}、S2={（202.5°，247.5°］}。该过程的实现对应复合算法COM_PR（）第一部分的for循环，其中引理1与定理1的正确性已证明完毕。

利用第三个for循环可得Tile-union（S1，S2）={ （202.5°，247.5°］：（292.5°，337.5°］，（202.5°，247.5°］：（247.5°，292.5°］，（202.5°，247.5°］：（292.5°，337.5°］： （247.5°，292.5°］}。该过程的实现对应复合算法COM_PR（）第二部分的for循环，其中引理2的正确性已证明完毕。

利用第四个for循环可得复合结果（202.5°，247.5°］：（292.5°，337.5°］的比例关系是（202.5°，247.5°］（70%）：（292.5°，337.5°］（30%），其余同理。该过程的实现对应复合算法COM_PR（）第三部分的for循环，且定理2的正确性已证明完毕。最后将角度形式的空间方向关系转换为SW（70%）：NW（30%）、SW（63.64%）：W（36.36%）、SW（50%）：NW（21.43%）：W（28.57%）。因此，NW（30%）：SW（70%）与W（40%）：S（60%）复合的结果包括SW（70%）：NW（30%）、SW（63.64%）：W（36.36%）、SW（50%）：NW（21.43%）：W（28.57%）三种情况。为验证该推理结果的正确性，进行手工推理，其手工推理的所有可能的空间布局如图8所示，可得算法COM_PR（）的推理结果与实际情形一致。

为了进一步验证COM_PR（）算法的正确性和完备性，通过第二个实例将COM_PR（）算法的推理结果与文献［18，23］的方法的推理结果进行对比分析。例如，源目标对象a与参考对象b、c的空间方向关系是a W（100%） b、b W（40%）：SW（60%） c。

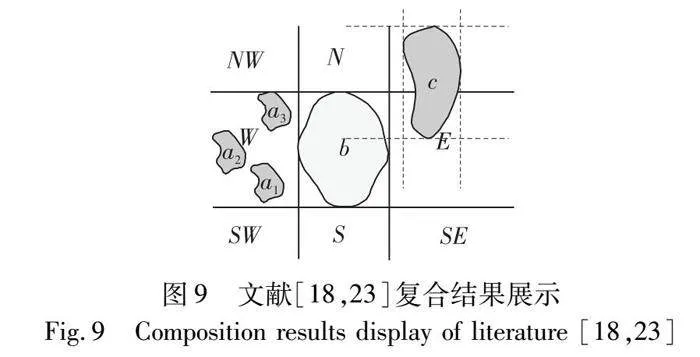
在文献［23］中提出的复合推理方法采用自然语言描述方向关系矩阵模型，仅对部分定义、定理进行形式化描述，给出了复合思想框架，计算218种基本主方向关系，针对W（100%）W（40%）：SW（60%），通过预处理Br运算和Most运算，得到复合结果是{SW，W，SW：W}，如图9所示。

在文献［18］中提出了一种改进的二维基本主方向关系复合推理方法，形式化描述文献［23］的复合思想，并对其进行细化，简化了Most运算，降低了复合的复杂性，针对W（100%）W（40%）：SW（60%），依次转换为方向关系矩阵复合，得到复合结果仍是{SW，W，SW：W}，如图9所示。

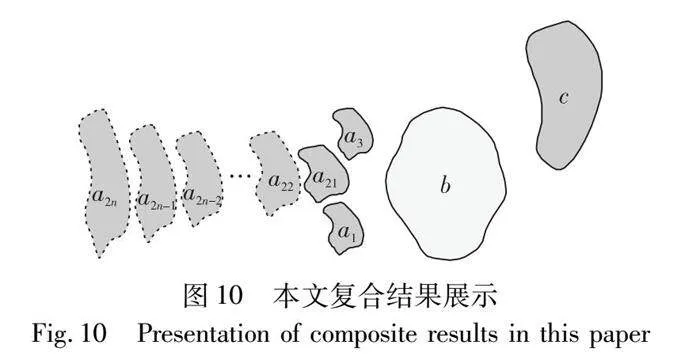
COM_PR（）算法利用方位角描述空间方向关系，在传统复合推理算法的基础上增加了Tile-union运算和Pr运算，得到复合结果是a SW（100%） c、a W（100%） c、a W（40%）：SW（60%） c。a SW（100%） c表示源目标对象a在参考对象c的西南面，如图9所示的空间对象a1、b、c的方向关系；a W（40%）：SW（60%） c表示最大范围内源目标对象a的40%在参考对象c的西面、60%在参考对象c的西南面，如图9所示的a21、a22、a23、…、a2n与参考对象c的方向关系；a W（100%） c表示源目标对象a在参考对象c的西面，如图10所示的空间对象a2、b、c的方向关系。综上，经上述三个复合推理方法的对比分析，可得本文的推理结果精度更高，推理结果给出了主方向关系中各原子主方向关系所占比例。

通过上述两个实例验证了COM_PR（）算法的正确性和完备性，COM_PR（）算法在传统复合推理算法的基础上增加Tile-union运算和Pr运算，使得推理结果具有明显优势，实现了非连通主方向关系的复合，提高了推理的精度，降低了复合结果的不确定性，该算法可以广泛应用于空间数据中的空间查询领域。

5 结束语

本文提出了一种基于Voronoi图的非连通空间对象方向关系表达模型，即VG-irregular方向关系模型，该模型较好地表达了区域空间对象间的方向关系，借助Gestalt心理学理论，经提取非连通空间对象的特征点、特征链，构建空间对象间的可视区域，生成方向关系Voronoi图，从而实现了非连通、含洞的空间对象间方向关系的精准描述，更加贴近真实的空间对象，并给出了该模型下非连通对象间主方向关系复合推理算法，该复合方法实现了非连通主方向关系间的复合，推理结果给出了主方向关系中各原子主方向关系所占比例，提高了复合推理的精度。

未来将围绕以下问题开展研究：

a）在本文提出的VG-irregular方向关系模型、二维主方向关系复合推理算法的基础上，结合现有的反关系推理、一致性检验等工作，将本文提出的Pr运算运用在二维主方向关系的反关系推理和一致性检验中，提高推理精度，实现二维主方向关系的反关系推理、一致性检验等问题的自动计算、推理和分析。

b）在本文研究的基础上，确立有效融合方向关系、距离关系和拓扑关系的方法。现有的结合方向关系、距离关系和拓扑关系的空间方位关系模型还无法真正实现三者的统一描述，实际上仍然使用各自相互独立的描述方法，缺乏统一的表达模型是影响表达和推理精度的主要障碍。

参考文献：

［1］郝忠孝. 时空数据库查询与推理 ［M］. 北京： 科学出版社，2010： 326-362. （Hao Zhongxiao. Query and reasoning of spatiotemporal database ［M］. Beijing： Science Press，2010： 326-362.）

［2］王淼，王晓桐，李松，等. 二维基本矩形主方向关系的原关系推理 ［J］. 西安交通大学学报，2020，54（4）： 133-143. （Wang Miao，Wang Xiaotong，Li Song，et al. The original relation reasoning of the principal direction relation of a two-dimensional basic rectangle ［J］. Journal of Xi’an Jiaotong University，2020，54（4）： 133-143.）

［3］董星星，高继勋，王晓桐，等. 空间方向关系表达与推理模型研究综述 ［J］. 计算机工程，2023，49（9）： 1-15. （Dong Xingxing，Gao Jixun，Wang Xiaotong，et al. A review of research on spatial directional relationship expression and inference models ［J］. Computer Engineering，2023，49（9）： 1-15.）

［4］王淼，方振西，王晓桐，等. 空间方向关系定性推理技术研究进展 ［J］. 计算机应用研究，2023，40（9）： 2561-2572. （Wang Miao，Fang Zhenxi，Wang Xiaotong，et al. Research progress on qualitative reasoning techniques for spatial direction relations ［J］. Computer Application Research，2023，40（9）： 2561-2572.）

［5］Gao Jixun，Li Mengmeng，Wang Miao，et al. A comprehensive model incorporating multiple spatial relations in 3D space ［J］. Recent Advances in Computer Science and Communications，2023，16（8）： 65-77.

［6］Wang Miao，Li Mengmeng，Fang Zhenxi，et al. Block algebra-based consistency checking with cardinal direction relations in 3D space ［J］. IEEE Access，2023，11： 130010-130021.

［7］Lark R M，Chagumaira C，Milne A E. Decisions，uncertainty and spatial information ［J］. Spatial Statistics，2022，50（18）：100619.

［8］Haar R. Computational models of spatialrelationa ［R］. College Park，MD： University of Maryland，1976.

［9］Papadias D，Sellis T. Qualitative representation of spatial knowledge in two dimensional space［J］. VLDB Journal，1994，3（4）： 479-516.

［10］Goyal R. Similarity assessment for cardinal directions between exten-ded spatial objects ［D］. Maine： The University of Maine，2000.

［11］闫浩文，郭仁忠. 基于Voronoi 图的空间方向关系形式化描述 ［J］. 武汉大学学报：信息科学版，2003，28（4）： 468-471. （Yan Haowen，Guo Renzhong. Formal description of spatialorientation relationship based on Voronoi diagram ［J］. Journal of Wuhan University：Information Science Edition，2003，28（4）： 468-471.）

［12］王淼，郝忠孝. 采用定性坐标的位置表达及主方向关系推理 ［J］. 西安交通大学学报，2010，44（8）： 36-41. （Wang Miao，Hao Zhongxiao. Position expression and principal direction relational reasoning using qualitative coordinates ［J］. Journal of Xi’an Jiaotong University，2010，44（8）： 36-41.）

［13］郝晓红，李松，郝忠孝. 复杂3D空间中的3DR46模型的表示与推理 ［J］. 计算机科学与探索，2020，14（12）： 2004-2013. （Hao Xiaohong，Li Song，Hao Zhongxiao. Representation and re-asoning of 3DR46 model in complex 3D space ［J］. Computer Science and Exploration，2020，14（12）： 2004-2013.）

［14］李朋朋，刘纪平，闫浩文，等. 基于方向关系矩阵的空间方向相似性计算改进模型 ［J］. 测绘科学技术学报，2018，35（2）： 215-220. （Li Pengpeng，Liu Jiping，Yan Haowen，et al. An improved model for calculating spatial orientation similarity based onorientation relation matrix ［J］. Journal of Surveying and Mapping Science and Technology，2018，35（2）： 215-220.）

［15］陈超，王中辉，马品. 面状群 （组） 目标空间方向关系的形式化描述与计算 ［J］. 测绘与空间地理信息，2021，44（9）： 17-21. （Chen Chao，Wang Zhonghui，Ma Pin. Formal description andcalculation of the spatial orientation relationship of surface group （group） targets ［J］. Surveying and Mapping and Spatial Geographic Information，2021，44（9）： 17-21.）

［16］王玉竹，闫浩文. 一种改进的群组目标空间方向关系计算模型 ［J］. 测绘科学，2022，47（4）： 169-174. （Wang Yuzhu，Yan Haowen. An improved model for calculating the spatial direction relationship of group targets ［J］. Surveying and Mapping Science，2022，47（4）： 169-174.）

［17］江坤，王中辉. 锥形模型的面群方向关系相似性度量方法 ［J］. 测绘科学，2022，47（6）： 174-180. （Jiang Kun，Wang Zhonghui. Similarity measurement method for surface group direction relationship of conical models ［J］. Surveying and Mapping Science，2022，47（6）： 174-180.）

［18］欧阳继红，孙伟，刘大有，等. 方向关系矩阵的复合 ［J］. 吉林大学学报：工学版，2010，40（4）： 1048-1053. （Ouyang Jihong，Sun Wei，Liu Dayou，et al. Composition of direction relationship matrix ［J］. Journal of Jilin University：Engineering Edition，2010，40（4）： 1048-1053.）

［19］顾卫杰，刘永山. 双投影矩阵模型的方向关系组合推理研究 ［J］. 测绘科学技术学报，2014，31（5）： 538-542. （Gu Weijie，Liu Yongshan. Research on direction relationship combination reasoning of double projection matrix model ［J］. Journal of Surveying and Mapping Science and Technology，2014，31（5）： 538-542.）

［20］Wang Miao，Liu Xiaodong，Li Songyang，et al. Composing 3D cardinal direction relations ［J］. Journal of Computational and Theoretical Nanoscience，2016，13（1）： 623-627.

［21］Li Song，Song Shuang，Hao Xiaohong，et al. Directional nearest neighbor query method for specified geographical direction space based on Voronoi diagram ［J］. High Technology Letters，2022，28（2）： 122-133.

［22］王淼，何莉，李松. 基本主方向关系的反关系推理 ［J］. 计算机应用研究，2013，30（1）： 138-141. （Wang Miao，He Li，Li Song. Inverse relationship reasoning of basic principal direction relationships ［J］. Application Research of Computers，2013，30（1）： 138-141.）

［23］Skiadopoulos S，Koubarakis M. Composing cardinal direction relations ［J］. Artificial Intelligence，2004，152（2）： 143-171.

［24］时玉，刘永山，王宝宗，等. 一种基于真实物体的主方向关系的合成算法 ［J］. 计算机工程与应用，2008，44（5）： 75-78. （Shi Yu，Liu Yongshan，Wang Baozong，et al. A synthesis algorithm based on principal direction relationships of realobjects ［J］. Computer Engineering and Applications，2008，44（5）： 75-78.）

［25］刘永山，成雪琴. 基于坐标映射模型的方向关系一致性检验 ［J］. 计算机工程，2011，37（16）：68-71. （Liu Yongshan，Cheng Xueqie. Consistency testing of directional relationships based on coordinate mapping models ［J］. Computer Engineering，2011，37（16）： 68-71.）

［26］Wang Miao，Fang Zhenxi，Liu Weiguang，et al. Computing the inverse of cardinal direction relations between regions ［J］. Journal of Intelligent Systems，2022，31 （1）： 1160-1177.

［27］Bukenberger D R，Buchin K，Botsch M. Constructing L∞ Voronoi diagrams in 2D and 3D ［J］. Computer Graphics Forum，2022，41（5）： 135-147

［28］王中辉，闫浩文. 基于方向Voronoi图模型的群组目标空间方向关系计算 ［J］. 武汉大学学报：信息科学版，2013，38（5）： 584-588. （Wang Zhonghui，Yan Haowen. Calculation of group targetspace orientation relationship based on Voronoi pattern model ［J］. Journal of Wuhan University：Information Science Edition，2013，38（5）： 584-588.）

［29］张云赫，苏立晨，董云帆，等. 基于Voronoi图最近邻协商的多机协同追捕方法 ［J］. 哈尔滨工程大学学报，2023，44（2）： 284-291. （Zhang Yunhe，Su Lichen，Dong Yunshan，et al. Multi machine collaborative pursuit method based on Voronoi graph nearest neighbor negotiation ［J］. Journal of Harbin Engineering University，2023，4W7mBpgdDTAUUuzVEGgDBtQ==4（2）： 284-291.）

［30］Izmirlioglu Y，Erdem E. Reasoning about cardinal directions between 3-D imensional extended objects using answer set programming ［J］. Theory and Practice of Logic Programming，2020，20（6）： 942-957.

［31］Zong Chen，Wang Pengfei，Yan Dongming，et al. Parallel post-processing of restricted Voronoi diagram on thin sheet models ［J］. Computer-Aided Design，2023，159： 103511.

收稿日期：2024-01-07；修回日期：2024-03-06 基金项目：国家自然科学基金资助项目（61802115，62173126）；河南省科技攻关项目（232102210068，232102210156，232102210085）；河南省高等学校重点科研项目（23A510018）

作者简介：王淼（1981—），男，河南光山人，副教授，博士，CC会员，主要研究方向为数据库理论与应用、空间关系、空间数据查询与推理等（wmscan@tom.com）；董星星（1998—），女，河南濮阳人，硕士研究生，主要研究方向为数据库理论与应用、空间关系等；高继勋（1980—），男，河南郑州人，教授，硕导，主要研究方向为图像处理、数据库理论与应用等；方振西（1996—），男，河南商丘人，硕士研究生，主要研究方向为数据库理论与应用、空间推理、空间关系等；唐昊（2000—），男，河南郑州人，硕士研究生，主要研究方向为空间推理、空间数据库理论与应用等；李松（1977—），男，江苏徐州人，教授，博士，主要研究方向为数据库理论与应用、数据挖掘、数据查询和推理.