乘法分配律的循证教学设计

【摘 要】乘法分配律是小学四年级数学课程的重要内容，是小学数学的教学难点。基于证据进行教学设计，可以有效提高教学的科学性。故按照循证教学设计模式，收集与整理乘法分配律教学设计的理论和实践证据，对乘法分配律进行基于证据的教学过程设计。

【关键词】乘法分配律；循证教学；教学设计

乘法分配律既是小学数学中多位数乘法、简便运算等内容的算理依据，也是中学数学中合并同类项、提取公因式等内容的知识基础，还是高等数学中推导矩阵性质等内容的指导性原理。乘法分配律是小学数学中的教学难点。有调查表明，将近95%的学生认为乘法分配律是运算律中最难学的。［1］127同时，部分教师也认为，乘法分配律比较难教。［2］91基于证据进行教学决策和实施教学行为，可使教学更有科学性。这里的“证据”是指经教育教学研究证实的，能够有效促进教学或规避教学问题的凭据。采用循证教学设计，对乘法分配律的教学进行深入探索，有助于师生双方共同突破这一教学难点。

一、乘法分配律循证教学设计的理论和实践证据

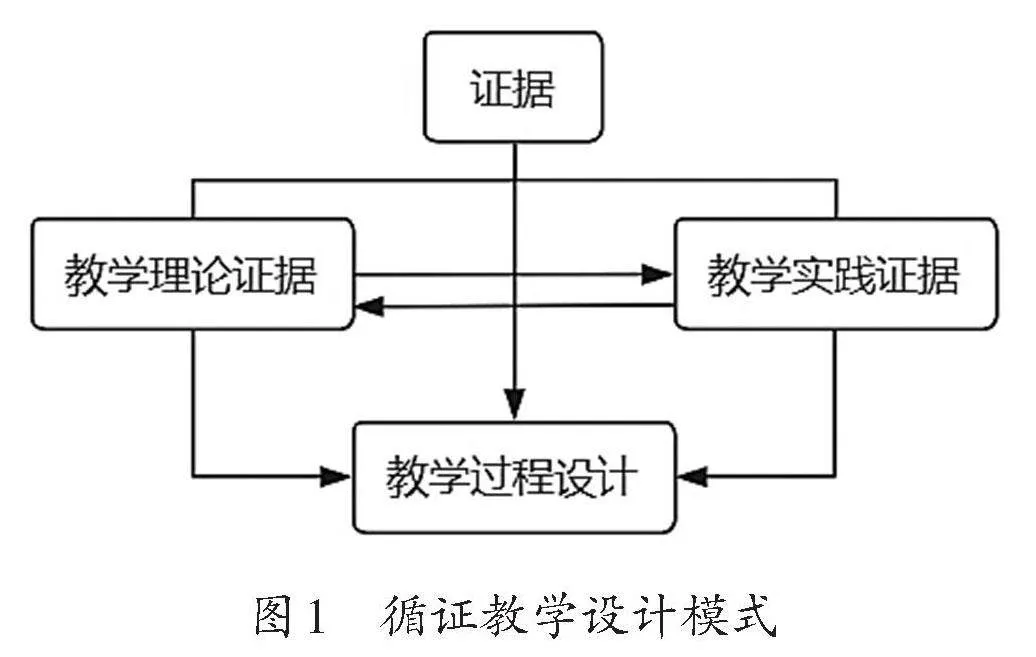
为了基于证据进行教学设计，需要深入探究教学理论证据和教学实践证据。教学理论证据为教学实践证据的搜集与整理提供了明确的方向，而教学实践证据中所揭示的特定教学实践困境，反过来又能指引教学理论证据的再找寻。如此，形成了以证据为导向，教学理论证据和教学实践证据相互作用，共同指向教学过程的循证教学设计模式（如图1）。下面结合循证教学设计模式，对乘法分配律循证教学设计的理论和实践证据予以说明。

（一）乘法分配律教学设计的理论证据

加涅根据信息加工理论构建了学习过程的基本模式，并强调教学需要通过合理安排可靠的外部条件来支持、激活和促进学习的内部机制。［3］教学设计属于学习的外部条件。依据加涅提出的教学事件与内部学习过程的对应关系，笔者设置了指引乘法分配律教学设计理论证据搜集的问题链：①如何设计教学情境以更好地吸引学生的注意力？②如何确立学习目标以激发学生的学习热情？③学生需要从长时记忆中提取哪些与乘法分配律相关的知识经验？④学生应从情境中提取哪些关键信息？⑤在理解乘法分配律时，学生可能会遇到哪些认知障碍？⑥在运用乘法分配律时，学生可能会遭遇哪些困难？⑦如何帮助学生更好地巩固乘法分配律？⑧如何引导学生迁移应用乘法分配律解决实际问题？

（二）乘法分配律教学设计的实践证据

以“乘法分配律”为主题和关键词，对公开发表的教学设计（实录）和教材比较等文献进行筛选，以此作为乘法分配律教学设计实践证据的重要来源。这一证据库汇聚了来自全国各地的丰富教学资源和教材分析，为乘法分配律的教学设计提供了全面的视角。结合理论证据提出的问题链，笔者对这些实践证据进行了系统整理，总结出促进有效学习的经验和可能干扰学习的教学问题。同时，也为进一步完善乘法分配律教学设计的理论支撑提供重要的参考。具体的乘法分配律教学设计理论和实践证据，详见下文的循证教学过程设计。

二、乘法分配律的循证教学过程设计

本研究以人教版教材四年级下册“乘法分配律”为教学内容，通过深入剖析乘法分配律与核心素养（推理意识、模型意识、符号意识、创新意识等）之间的内在联系，制定明确的教学目标。在此基础上，围绕“情境引入—探究新知—课堂练习—课堂小结—拓展思考”的流程设计教学，并在每个环节，结合具体的教学内容阐明这样设计的理论和实践证据。

（一）情境引入

实践证据表明，由于缺乏相关的生活经验，尤其是对挖坑、种树、抬水、浇树等植树的分工缺乏了解，学生普遍对教材中关于植树的情境感到陌生，因而无法产生探究的欲望。［4］45同时，学生容易误解情境信息（如把“4人负责挖坑、种树”理解为“4个人挖坑，4个人种树”），导致列出错误的算式。［5］15因此，教师需要对教材中的情境进行适当的调整。

问题1：请用综合算式，呈现以下三道题目的计算过程（如图2）。

通过学生的尝试和教师的引导，可得出以下三个综合算式（等式）：

14×（2+10）=14×2+14×10

（6+3）×3=6×3+3×3

175×4+125×4=（175+125）×4

【设计意图】在学生学习乘法分配律之前，教材已多次通过实际例子展示了乘法分配律的应用，帮助学生初步建立了分配意识。这些例子分别为二年级上册的乘加、乘减，三年级上册的多位数乘一位数，三年级下册的两位数乘两位数、长正方形组合求面积，以及四年级上册的三位数乘两位数、行程中的相遇问题，等等。为了帮助学生更好地理解和应用乘法分配律，笔者对这些已学过的数学知识进行归类，设计了上述三种学生熟悉的旧知情境引入教学，引导学生感知学习乘法分配律能帮助他们更加系统地理解这些“先行应用”的知识，从而使学生形成学习期待。而要求学生列出综合算式，则是为了防止学生过分依赖分步计算，从而使其更易于发现和理解乘法分配律的规律。

（二）探究新知

1.发现乘法分配律的规律

实践证据表明，直接告知学生乘法分配律的教学方式，其效果普遍不佳。通过单一等式来揭示一个共性规律，对学生来说不容易理解。［4］45基于发现学习理论，教师应设计相应的学习活动，让学生亲自经历知识的发现过程。［6］113因此，教师应提供相应的学习材料，让学生通过观察发现乘法分配律的规律。

问题2：仔细观察三个等式，你有什么发现？

14×（2+10）=14×2+14×10

（6+3）×3=6×3+3×3

175×4+125×4=（175+125）×4

教师应引导学生关注“两个数的和”与“一个数”之间的乘积关系，从而发现其背后的规律，即两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。

【设计意图】三个等式分别囊括乘法分配律的左右分配律及其逆运算。通过对这三个综合算式的比较，学生可以发现三个综合算式的数学结构，即“两个数的和”与“一个数”之间的乘积关系。

2.理解乘法分配律及其成因

实践证据表明，学生无法较好地理解乘法分配律的意义。［2］92根据探究学习理论，知识不应被当作绝对真理教给学生，而应作为有证据的结论。［6］135因此，教师可鼓励学生自主举例子进行论证，以深化对乘法分配律及其成因（即是什么和为什么）的理解。

问题3：你能再举几个类似的例子吗？并说明为什么等式两边相等。

教师可以引导学生通过计算验证、“几个几”的算理验证、点子图的数数验证和几何图形的面积验证等多种方式说明等式左右两边相等。

【设计意图】论证说明所举等式两边相等的过程，不仅有助于学生建构数学模型，还能培养他们因果推断的意识。

3.乘法分配律的表示方法

乘法分配律的文字定义：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加，这叫作乘法分配律。基于此，教材用字母a、b、c表示乘法分配律，引导学生感悟乘法分配律模型的普适性，从而培养学生的模型意识，使他们认识到符号表达运算规律具有一般性，渗透符号意识。然而，实践证据表明，由于字母a、b、c较为抽象，学生在使用公式进行计算时，容易混淆乘法分配律与乘法结合律［1］127，这与使用相似的字母a、b、c，导致二者区分度较低有一定的关系。为此，教师需要引导学生对教材的表示方法进行调整。

问题4：用字母怎么表示乘法分配律？

教师应引导学生将教材中的字母a、b、c更换为字母m、a、b，并用字母m表示“一个数”，用字母a+b表示“两个数的和”，从而区分乘法分配律与乘法结合律以及“一个数”与“两个数的和”。

据此，乘法分配律可以表示为：m×（a+b）=m×a+m×b或（a+b）×m=a×m+b×m。

【设计意图】通过字母a、b的紧密性，确保“两个数的和”作为一个整体思想得以延续。同时，m在公式中的不变性使分配过程具象化，即m穿透括号分别与a、b作用。［7］这种方法降低了学生的认知负荷，突破了将文字语言转化为符号语言表述乘法分配律的实践难题。

（三）课堂练习

涉及乘法分配律的变式应用具有高度的灵活性，往往会给学生带来运用上的困难。因此，笔者结合实践证据，设计了一系列需要对比辨析的练习题，帮助学生突破易错点和易混淆点。

问题5：（1）下面哪些算式是正确的？正确的画“√”，错误的画“×”，并说明理由。

56×（19+28）=56×19+28 （ ）

32×（7×3）=32×7+32×3 （ ）

（2）计算题。

计算99×101。

计算99×57+99。

【设计意图】设计上述练习题旨在解决乘法分配律应用中以下几类易错点和易混淆点：①正向应用乘法分配律公式的易错点，即a×（b+c）=a×b+c［8］；②与乘法结合律混淆的易错点；③需灵活拆分数的乘法分配律简便运算难点［2］92；④需识别省略或补上乘数1的乘法分配律逆运算难点［1］127。

（四）课堂小结

实践证据表明，学生课后遗忘乘法分配律的速度较快。［4］45本研究采取结构化整合的教学策略，引导学生沿着“数学思维—数学结论—数学价值观念”的结构化整合路径，对乘法分配律的学习进行回顾与反思，旨在帮助学生构建紧密关联且可持续发展的乘法分配律图式。

问题6：本节课经历了怎样的探究过程？得到了什么数学结论？运用了哪些数学思想方法？体会到了哪些数学价值观念？

【设计意图】通过一系列问题，在帮助学生巩固乘法分配律相关知识的同时，让学生反思乘法分配律的发现过程及其中蕴含的思想方法，从而感悟数学的思维训练价值、发现创新价值和学科育人价值。

（五）拓展思考

学生在掌握乘法分配律后，会产生“有除法分配律吗？有三个数的和与一个数相乘的规律吗？”［5］15等疑问。为了满足学生对未知的探索需求，并借此机会提供强化练习，特设计以下拓展思考内容。

问题7：（1）在（ ）里填上适当的数。

167×2+167×3+167×5=167×（ ）

28×225−2×225−6×225=（ ）×225

39×8+6×39−39×4=（ ）×（ ）

*（2）如果m、a、b代表任何数字，符号□和■代表+、−、×、÷中的任何一个，等式m□（a■b）=m□a■m□b什么时候成立？

总是（ ） 从不（ ） 有时当（ ）。

原因： 。

【设计意图】选择教材中的※号题，适度拓展乘法分配律的应用范围，编制一些更具推广意义的一般性思考题。鼓励学生勇于探索一些开放性、非常规的数学问题，这有助于培养学生的创新意识和数学素养。

虽然基于证据的教学设计从理论层面确保了教学决策的科学性，但是其实际教学效果仍需经过实践的检验。期望广大一线教师能够积极践行循证教学理念，并通过教学反思与再实践，不断充实和完善教学证据库。

参考文献：

［1］王婵丹.深度理解“原型”是掌握多样变式的根本策略：以“乘法分配律”练习课的教学为例［J］.小学教学设计（数学），2023（1/2）：126-130.

［2］吴晓雄.数形结合 突破难点：“乘法分配律”教学新探索［J］.小学教学研究，2022（18）：91-94.

［3］加涅.学习的条件和教学论［M］.皮连生，王映学，郑葳，等译.上海：华东师范大学出版社，1999.

［4］安安.不断反思 不断改进：《乘法分配律》的试教及改进［J］.教育理论与实践，2007（14）：45-47.

［5］朱乐平.如何研究一节课的数学教材？：以“乘法分配律”的教材研究为例［J］.教学月刊·小学版（数学），2021（7/8）：12-16.

［6］陈琦，刘儒德.当代教育心理学（第3版）［M］.北京：北京师范大学出版社，2019.

［7］徐小琴.关于乘法分配律的几点慎思与求索［J］.教学与管理，2020（11）：32-34.

［8］陈金飞.“乘法分配律”数学模型的建构［J］.教学与管理，2015（5）：43-44.

（1.上海师范大学教育学院

2.内江师范学院教学科学研究院）

*本文系2020年四川省教育科研资助金项目重点课题“差错诊断与差错控制——数学教与学解困新路探究”（课题编号：SCJG20A049）的研究成果。赵思林为本文的通讯作者。