顺应认知规律 形成概念结构

【摘 要】平行与相交既是表述两条直线位置关系的两个基本概念，又是描述图形特征的关键要素。教学中，可引导学生通过观察平行四边形，从中分离出“平行”这一概念，进一步经历找平行、画平行、判断平行，以及旋转、平移与捆绑等数学活动，完善对平行的认识，并在此基础上，在生活中、平面图形和立体图形中分别寻找平行，体会平行多元的存在形态。

【关键词】认知规律；概念结构；平行与相交；位置关系

平行与相交既是表述两条直线位置关系的两个基本概念，又是描述图形特征的关键要素。在先前的学习中，通过识别长方形、正方形、三角形、平行四边形等图形，学生对线段间的位置关系有了初步的认识。因此，学习平行与相交的概念，既是对已有学习经验的总结，也为后续进一步学习图形的特征打下了基础。基于这样的认识，在具体教学中，如何选择合适的学习材料，让学生利用已有的活动经验进行观察、比较和分析，以辨认平行与相交？如何有层次地结合具体例子，给“平行”“平行线”和“互相平行”下定义？应该设计哪些操作活动，让学生根据“平行线”的特征，运用多种方法画平行线？带着这样的思考，笔者进行了如下教学实践。

一、基于概念名称，直观感知平行

平行既是一个数学概念，也常用于日常交流。从平行中的“平”字来看，它包含“平平的”的含义。在学生熟悉的平行四边形这一概念中，便蕴含了“平行”的元素。那么，学生是如何通过平行四边形这一概念来理解平行的呢？笔者将以此为起点，引导学生直观地感知平行。

（一）通过名称，感知平行现象

教师出示图1，请学生观察后回答：“你认识这个图形吗？”在实际教学中，有学生指出这是一个四边形，教师进一步追问：“为什么这么说？”学生解释因为它由四条边组成。有学生指出它是平行四边形，教师特别强调“平行”这一部分，并追问：“为什么又叫‘平行——四边形’？”学生解释因为它是“平平的”，即上下两条边是平行的。

通常，平行通过生活中的原型来引出，并用“……不相交”这样的句式来概括。即先认识“不相交”的现象，再将这种现象定义为“平行”。因此，笔者尝试从学生已有的概念名称——平行四边形中的“平行”的解释入手，引导学生感知平行的表象。

（二）借助工具，画不同平行线

显然，此时学生对平行的理解是基于“平行”的字面含义形成的直观认识。为了深入理解平行的本质特征，教师需要借助工具，画出不同的平行线。

教师出示一块长方形模型（如图2），引导学生观察其上下两条边是否平行。学生确认平行后，教师再将两条边用粉笔描到黑板上。接着，教师将长方形模型斜放，再次提问：“这两条边还平行吗？”学生观察后指出，即便倾斜，这两条边仍然平行。教师再次在黑板上用长方形模型画出斜的一组平行线（如图3）。

（三）结合反例，概括平行特征

结合图2、图3中的两组平行线的例子，教师引导学生进一步观察图1中的平行四边形。除了“平平的”一组平行线外，学生还指出存在一组“斜斜的”平行线。教师顺势让学生用手势分别演示“平平的”和“斜斜的”的平行线。

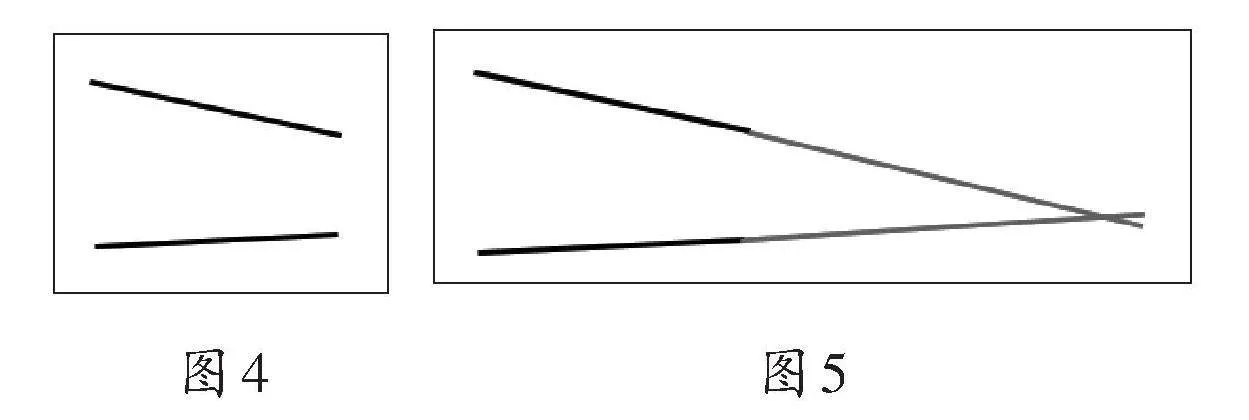
接着，教师在两组平行线的旁边画出一组直线（如图4），并请学生判断它们是否平行。学生经过比较，认为它们不平行，并解释如果将两条直线延长，它们最终会相交。教师根据学生的回答进行验证，得到图5。

教师引导学生回顾，在平行四边形中发现了两组平行线，在黑板上也画出了两组平行线，并且还发现了像图4中这样的两条直线最终会相交。启发学生思考：我们这里说的平行在研究什么？怎样叫作“平行”呢？

最后，组织学生进行交流讨论，形成图6所示的板书，并总结：在研究两条直线的位置关系时，存在两种情况，一种是相交，另一种是平行，平行即两条直线不相交。在归纳出平行的特点后，再用字母分别表示平行中的两条直线。

通过对平行四边形中“平行”概念的多轮解释，学生逐步概括出平行线的特点，认识到平行是指两条直线的位置关系。然而，目前得到的平行线概念尚不完善，需要通过更多有针对性的例子来进一步完善。

二、结合操作活动，完善平行概念

“不相交的两条直线”就是平行线。显然，这一定义需要补充一个前提条件——这两条直线必须在同一平面内。判断两条直线是否互相平行，除了延长直线的方法，还可以采用平移的方法进行验证。为了利用平移验证平行线，教师引导学生使用捆绑铅笔的方法来画平行线。

（一）利用教具，明晰概念范畴

在从长方形模型中描出不同位置的平行线，并从中概括出平行的特点后，教师继续操作教具，将表示其中一条直接的木条绕中间的连接点旋转一定角度，形成图7中右侧的样子。然后引导学生判断：此时两条直线是否仍然平行？学生观察后指出：“不平行。”教师追问：“那么它们会相交吗？”学生回答：“不会相交。”

教师根据学生的回答提出问题：“为什么这两条直线既不相交，也不平行呢？”学生观察后指出，因为这两条直线的方向不同。也有学生进一步指出，它们不在同一个平面内。教师根据学生的回答，在图6中补充了“在同一个平面内”这一前提条件。

（二）验证平行，完善认识结构

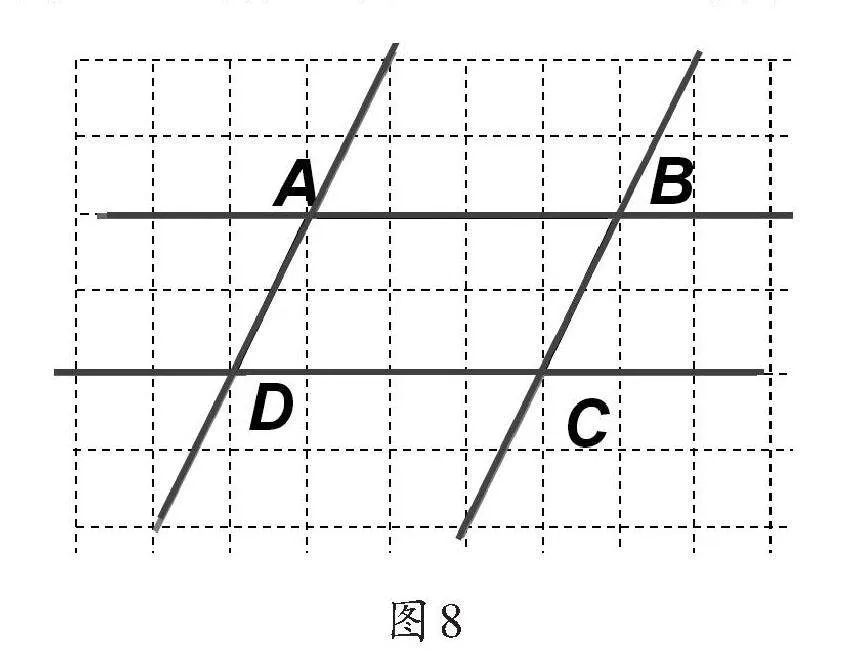
教师请学生观察图1中的两组平行线，并讨论可以使用哪些方法来验证这两组线段是平行线。学生指出可以通过延长线段来观察是否相交，如果不相交就是平行。教师依据学生的回答，分别延长两组线段，发现没有相交（如图8）。教师追问：“请仔细观察，是否还有其他方法可以验证它们平行呢？”

在实际教学中，有学生观察后发现，可以将其中的一条直线平移，看是否可以与另一条直线重合。教师根据学生回答，将直线AB向下平移，与直线CD重合，并总结：直线AB平行于直线DC；然后将直线CD向上平移，与直线AB重合，并同样总结：直线CD平行于直线AB。进而综合两句话得出：直线AB与直线CD互相平行使学生直观地认识“互相”的含义。

（三）依据特征，创造工具画平行

小学阶段并未涉及使用平移三角板的方法画平行线，但教师可以利用平行的特征，引导学生通过捆绑两支铅笔的方式画平行线，这也是教材练习十第5题所倡导学生学会画平行线的方法。在本教学环节，教师鼓励学生自己创造出这种画平行线的工具。

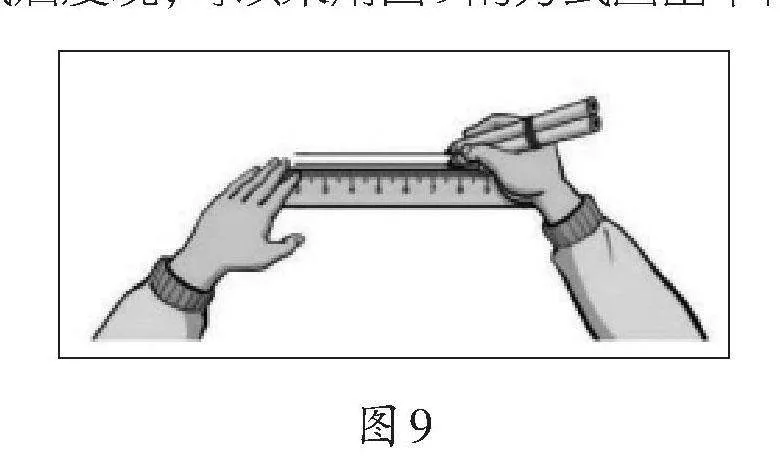
教师首先请学生回顾黑板上的两组平行线是怎样画成的。学生指出，这些平行线是通过描出长方形模型的两条对边而形成的。随后，教师提出了一个新挑战：如果没有这样的长方形模型，仅使用两支铅笔和三角板，你能够画出一组平行线吗？教师让学生先独立尝试，之后再进行交流和反馈。学生尝试后发现，可以采用图9的方式画出平行线。

在成功画图后，教师引导学生反思：为什么用这一种方法可以画平行线？学生通过观察发现，由于两个笔尖之间的距离保持不变，因此画出的两条直线之间的距离处处相等，从而确保了它们不会相交。

通过旋转、平移与捆绑等操作活动，学生对平行的理解得到加深，特别是认识到“互相平行”的概念可以通过动态的平移现象来解释。

三、探索多元平行，拓展存在形态

“平行”这一概念在日常生活及各类图形中以多种形态存在。在教学中，学生需依据定义进行抽象思考，以感受平行在日常生活中的多样存在形态。

（一）结合图式，寻找生活中的平行

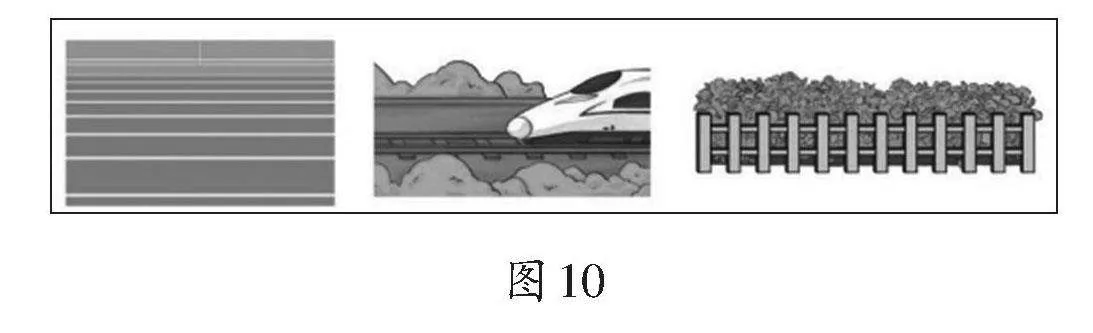
教师出示图10，请学生说一说图中画的是什么，并描出其中的平行线。学生独立完成后进行反馈。在此基础上，教师鼓励学生列举生活中有关平行的例子，尤其是教室内的实例。

（二）观察图形，寻找平面中的平行

教师出示图11的两个图形，要求学生识别并写出图形中的平行线，并说一说有什么发现。学生先独立完成，再进_{301d6e98f150363fe172a7c9b55599c90591207667f9960d55d0c5bd5ba5df30}行交流反馈。在确认学生理解后，教师引导学生观察a∥b、b∥c、c∥d的情况（图略），并说一说自己的发现。学生讨论后，教师概括：如果a∥b、b∥c，那么 c∥d，这三条直线两两平行。从而让学生体会到平行线的传递性。

（三）发挥想象，发现立体中的平行

在立体图形中寻找平行线，需要学生发挥想象，构建新的平面图形。教师出示图12所示的立体图形，要求学生找一找与边AB平行的其他边。学生独立完成后进行交流评析。

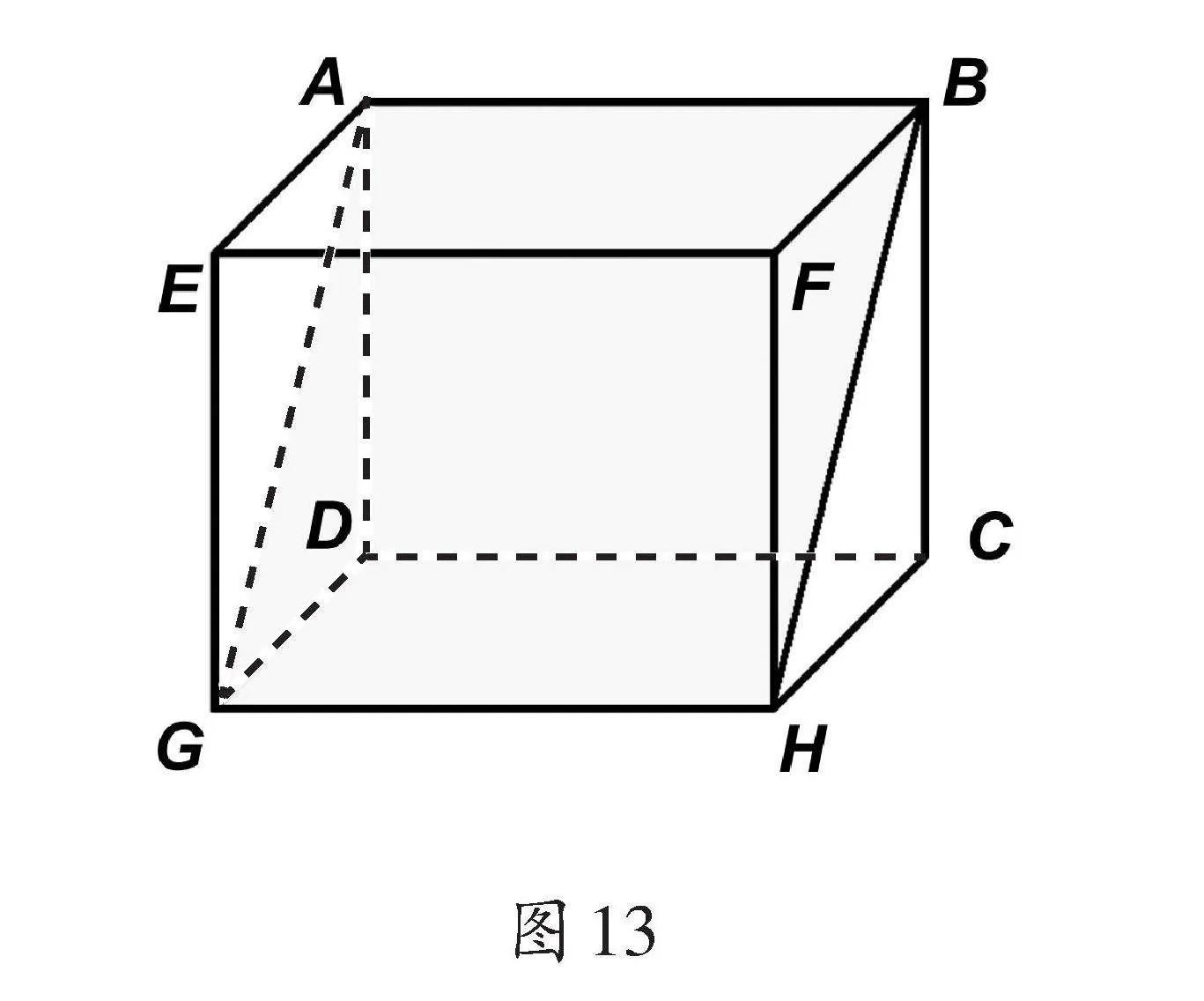
学生发现：AB∥EF、AB∥DC、AB∥GH。教师引导学生质疑：AB和GH不在同一个平面内，怎么它们也互相平行呢？学生提出可以通过连接A、G和B、H来构建平面ABHG。教师根据学生的回答，用课件动态演示（如图13）。接着，教师请学生观察，在AB、EF、DC、GH这四条边中，还有哪两条边也是互相平行的。学生回答后，教师概括：AB、EF、DC、GH互相平行。基于这一发现，教师要求学生找一找，在立体图形中还有哪些边也是互相平行的。学生独立完成后校对答案。

在进一步的探讨中，教师引导学生思考：在立体图形中，除了直线之间的平行关系，是否还存在“面”与“面”之间的平行呢？学生经过观察指出，上面与下面、前面与后面、左面与右面这些相对的面都是平行的。教师进一步指导学生通过延长两两平行的线段来验证这一结论，图14是验证上面与下面两个面平行的示意图。

本节课的教学实践为教师提供了重要启示。图形的认识经历从整体感知到特征概括的过程。对于“平行”“相交”等概念的学习，需要从图形整体认识出发，对图形要素进行特征分析，从而为深入理解图形特征打下坚实的认知基础。因此，对于这些概念的学习，可以从图形的整体认识中分离出来，通过观察、比较、操作等数学活动，逐步完善对概念的理解。

（1.浙江省湘湖师范学校附属小学

2.浙江省杭州市余杭区百丈镇中心小学）