以游戏为介 探推理之妙

【摘 要】数学游戏的外在形式表现为感性，其数学内涵体现为理性。以数学游戏“寻找聪明的猴王”的教学为例，在游戏设计过程中借助主题式的情境，对游戏元素和数学规律进行结构化整合。该游戏属于探究型游戏，其组织方式遵循“理解规则，大胆猜想—举例验证，概括结论—迁移应用，逆向思考”的原则。教学中，教师引导学生运用画图呈现、列表归纳、符号表征规律等方法，促进学生思维能力的进阶。

【关键词】探究型游戏；探索规律；推理意识

数学游戏的外在表现形式虽然充满感性色彩，但其数学内涵却基于严谨的理性思维。“寻找聪明的猴王”这一游戏属于探究型数学游戏，这类游戏通过情境中的问题驱动，让学生运用逻辑推理来分析和解决问题，其目的在于培养学生的批判性思维和解决问题的能力。

一、游戏解读与定位

（一）游戏概述

数学游戏“寻找聪明的猴王”的主题源自约瑟夫问题（也称“约瑟夫环原理”），要求游戏者借助二进制原理来解决问题。在设计过程中，教师将数学内容嵌入到引人入胜的问题情境中，采用叙述故事的方式，激发学生主动参与游戏，引导他们探索问题。

【故事情境】在猴山中，年迈的老猴王即将退位，需要从群猴中选出一只聪明的猴子担任新猴王。考核的项目是确定位置，在一场报数淘汰的游戏中，能够留到最后的猴子将成为新猴王。

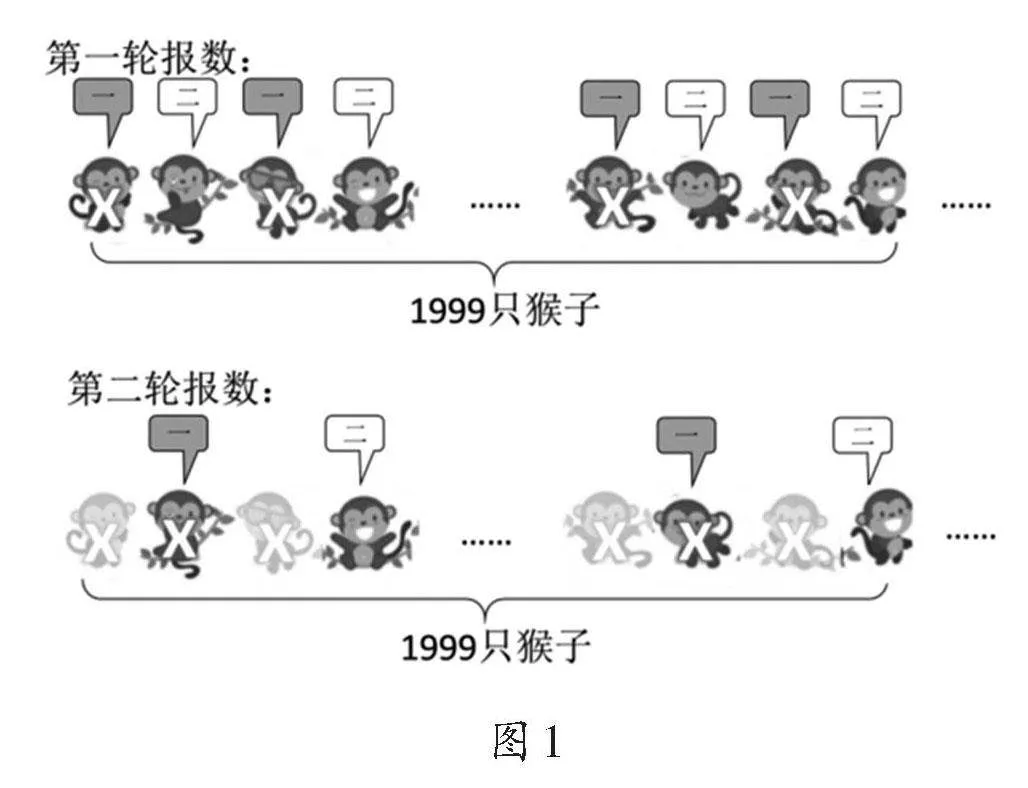
【游戏规则】猴山上的1999只猴子按顺序排列并编号，“一二一二”地进行报数。每次报到“一”的猴子即被淘汰，剩余的猴子在下一轮重新报数，重复此过程，直至最终仅剩一只猴子，即为猴王，如图1所示。

该游戏属于探究型游戏，其组织方式遵循“理解规则，大胆猜想—举例验证，概括结论—迁移应用，逆向思考”的原则。

由于学生直接猜测1999只猴子的结果过于复杂，教师可引导学生采取“化繁为简”的数学方法，从较小的数开始尝试。在数量较少的情况下，谁会是最后的胜者？任何猜想都需经过验证，因此，学生须通过画图枚举、表格列举归纳等方法进行验证。首先，从简单到复杂，逐步发现猜想的不足之处，并进一步探寻“找猴王”背后的规律。其次，使用符号表示一般规律，构建解决问题的路径。最后，在迁移应用环节，从猴子数量到猴王编号的正向映射，以及从猴子编号逆向推理出猴子数量的范围，学生将初步感知分段函数的特征以及指数函数的变化趋势。

（二）目标定位

数学游戏“寻找聪明的猴王”被整合进五年级数学课程的教学计划中，旨在让学生在探究过程中经历问题解决的全过程。

1.理解规则，培养规则意识

游戏的开展基于对游戏规则的理解。教师通过角色扮演、想象验证、画图表达等方式帮助学生掌握游戏规则，并在此过程中培养学生的规则意识。

2.自主探究，培养推理意识

通过自主探究和归纳推理，进一步感知数学的一般规律，建立简单的数据模型，并探索解决问题的策略。学生通过辨析比较和举例验证，推理出猴子数量与猴王编号之间的联系。

3.优化方法，锻炼逆向思维

在开展数学游戏的过程中，教师鼓励学生寻找更为简洁的解决方式，进行逆向思考，从简单的数学规律出发，建立相应的对应关系，以此锻炼学生的逆向思维能力。

二、游戏实施过程

（一）理解规则，大胆猜想

教师通过创设生动有趣的游戏情境，激发学生的探究欲望。对游戏规则的理解，学生需经历“理解—提炼—简化”三个阶段。

【教学环节1】

1. 大胆猜想，初步理解规则

师：请大家大胆地猜一猜1999只猴子循环报数，站在几号的猴子会留到最后呢？

生：我选1999号，因为是最后一个编号，可能会留到最后。

生：按照“一二一二”报数的规则，编号是奇数的猴子会报“一”，1999号第一轮就会被淘汰，我猜猴王是1998号。

生：我猜可能是1000号，因为每次都会淘汰一半左右，猴王的编号可能会接近中间数。

师：究竟最终的猴王是几号呢，你们打算怎么研究？

生：我们可以用小棒表示猴子，通过摆一摆来模拟选猴王的过程。

生：这里可能蕴含着一个规律，但1999只猴子数量较多，我们可以减少一些数量来看看有什么规律。

师：当数量比较多或问题比较复杂时，我们可以采用“化繁为简”的数学方法，不妨先从8只猴子开始尝试。

2. 借助演示法，熟悉规则

（教师请8个学生上台来模拟游戏，学生排好队后，并逐一编号）

师：大家猜一猜，谁会留到最后？我们先来试试，开始报数。请报到“一”的同学出列。大家发现了什么？

生：报“一”的猴子的编号都是奇数，所有编号是奇数的猴子在第一轮就会被淘汰。

师：思考第二轮会淘汰哪些编号为偶数的猴子？为什么？大家可以用画一画、写一写或表格罗列的方法寻找谁留到最后，并想一想这个结果背后的数学规律。

生：在第一轮淘汰后，所有编号为偶数的猴子全部留了下来，它们的编号是②④⑥⑧。它们重新报数，报“一”的第1位和第3位被淘汰，报“二”的第2位和第4位留了下来（如图2）。

生：每次重新报数的过程，相当于给猴子们重新编号。每轮报数都是把奇数位置上的猴子淘汰掉，把偶数位置上的猴子留下来。

“寻找聪明的猴王”这个数学游戏的规则简单明了，但还是存在难懂之处：当留下的猴子编号全是偶数时，哪些猴子会被淘汰？教师借助演示法，让学生参与到主题式情境中理解规则。在演示的过程中，教师鼓励学生基于操作进行思考，用画一画、写一写或列表格的方法呈现思考过程，并进一步理解游戏规则。

（二）举例验证，概括结论

数学游戏的探索过程是发展思维能力的过程。对于从形象思维向抽象思维过渡的小学生而言，探究需要经历一个过程。游戏经历了一个“从20以内数的列举—超过20的数的推理—表格归纳”的过程，鼓励学生使用符号化语言表达思考过程，逐步揭示其中的规律和联系。

【教学环节2】

1.初次尝试，假设推理

师：先前假设了8只猴子，留到最后的是8号位置。如果是10只猴子、20只猴子呢？请在20以内的数中任选一个，先预测最后留下的位置编号，再把思考过程记录下来。

生：我选的是10只猴子。我猜想是10号留下来，但验证后发现不对，10号在第二轮报数时就出局了。

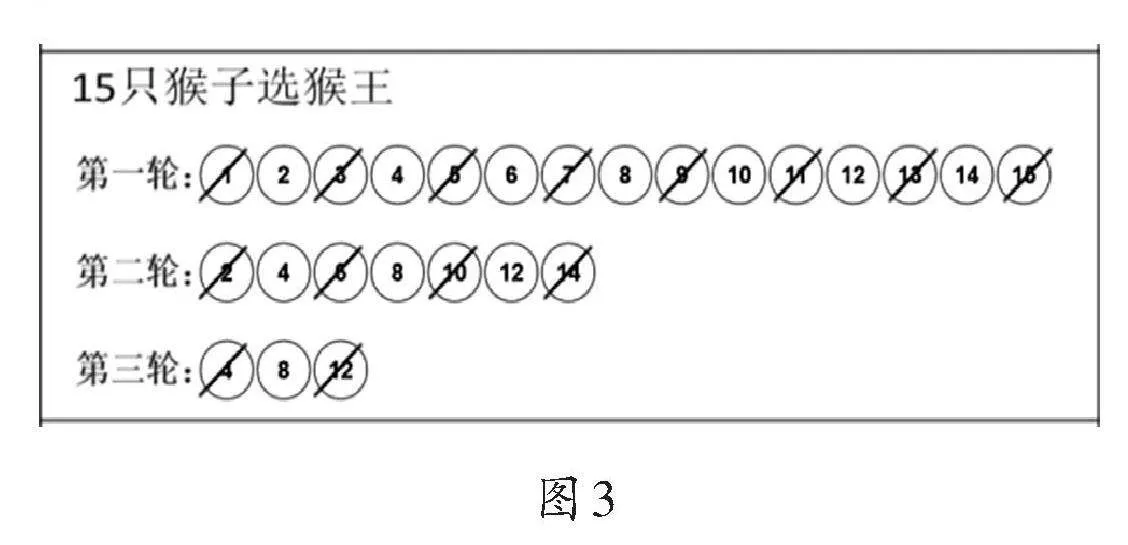
生：我选择了15只猴子。预测是10号留下，最后是8号留下来，原因是8号在每一轮报数中，都位于偶数位置上（如图3）。

生：当有20只猴子时，经过四轮淘汰后，留下的是16号。

师：10只猴子、15只猴子，数量不同，为什么最后留下的都是8号，而20只猴子留下的却是16号呢？

教师通过假设20以内数，引导学生思考“猴子数量不同但猴王位置相同”和“猴子编号是8号和16号不同”的原因。学生通过两次辨析讨论，借助互动式学习，在辨析“变”与“不变”中，充分感悟每一轮淘汰筛选的过程，积累活动经验。

2.拓展假设，归纳推理

师：当猴子的数量大于20只时，你能否找到猴王的编号？请你自由拟定猴王的数量，预测猴王的编号，再通过画图或列表验证你的猜想。

（先让学生自主尝试，再组织学生反馈作品，如图4所示）

生：我想验证猴子数量为23只时，猴王编号是否也是16号。我画了一张图，每次淘汰时，我都重新对猴子进行编号，奇数位的猴子都被淘汰，剩下的是16号，我的猜想是正确的。

生：我预测猴子数量为84只时，留下的猴子编号为64号。84÷2=42，第一轮报数后留下了42只猴子，这些猴子的编号都是2的倍数；第二轮报数后留下的猴子编号都是4的倍数；第三轮报数后留下的猴子编号都是8的倍数……当第六轮报数后留下的猴子编号是64的倍数。

教师鼓励学生将数学活动经验进行迁移，推理“超过20只猴子”时的情况。学生可以借助图式验证推理结果，也可以通过观察图式中的信息，提取出算式进行推理。

3.表格汇总，抽象推理

师：刚才我们都是自由假设一个具体数量进行探究，现在将大家探究的情况汇聚在一张表格中，你们能否继续找出猴王的位置编号，并想一想其中的奥秘？

（教师出示表1）

（呈现表格，让学生自主探究，并进行交流讨论）

生：我发现猴王编号为2号、4号、8号、16号、32号，编号依次乘2，之后应该是32×2=64号了。

生：猴子数量与猴王编号之间存在联系。我推测当猴子数量为32～63只时，猴王编号均为32号。

学生“补全表格”的过程是培养推理能力的过程。他们在表格中感受数据的变化，寻找数据之间的联系，得出结论并对其原因进行解释。学生掌握了合情推理的方法，能够找到“猴子数量与猴王编号”之间的对应关系。

（三）迁移应用，逆向思考

在解决1999只猴子的问题时，尽管前述方法能够解决问题，但过程颇为复杂。当正向思考“已知猴子数量，求猴王编号”受阻时，教师可以引导学生逆向思考，将问题转化为“已知猴王编号，求猴子数量的范围”。逆向思考可以显著提高解决问题的效率。

【教学环节3】

师：通过推理活动，大家已经掌握了确定猴王编号的方法。在确定猴王编号时，可以借助画图、列式、列表等方法。设想一下，使用这些方法研究1999只猴子的过程，你们有什么感觉？

生：虽然这些方法可以解决问题，但这张图太长了，算式太多了，表格太大了。

师：猴王编号有规律吗？与猴子数量有什么联系？

（先让学生独立思考，再进行小组讨论并汇报）

生：猴王编号为2号、4号、8号、16号、32号，后续编号我们已经推理并验证了是64号，即这些编号依次乘2。

生：当猴王编号是2号时，对应的猴子数量为2～3只；猴王编号是4号时，对应的猴子数量为4～7只……猴王编号是几号，对应的猴子数量就从几开始。

（根据学生的回答，逐步抽象出数学规律，如图5所示）

师：通过初步尝试，自主假设，表格汇总，我们发现了猴王编号和猴子数量之间的联系。那么，它们之间究竟存在怎样的联系呢？聪明的猴王应该站在哪个位置才能确保留到最后？

生：对于1999只猴子，其数量处在1024～2047这个范围中，位于<I：＼教学月刊社暑期工作（祖后宁）＼小学版＼小学数学＼小学数学2024-10＼教学月刊-小学数学2024第10期内芯＼Image＼image6_4.png>和<I：＼教学月刊社暑期工作（祖后宁）＼小学版＼小学数学＼小学数学2024-10＼教学月刊-小学数学2024第10期内芯＼Image＼image7_3.png>之间，因此猴王应站在1024号位置，这样才能确保留到最后。

生：猴王编号为 <I：＼教学月刊社暑期工作（祖后宁）＼小学版＼小学数学＼小学数学2024-10＼教学月刊-小学数学2024第10期内芯＼Image＼image8_3.png> ，猴王编号对应的猴子数量范围从这个数开始。

从策略的探究、提炼到应用，从规律迁移到规律应用，体现了逻辑推理的价值。教师将数学知识融入“寻找聪明的猴王”这一特定的游戏情境中，以问题为驱动激发学生的学习动力。教学中，教师鼓励学生表达思考过程、描述推理过程、提炼关键信息，构建简单的数据模型，并引导学生运用画图呈现、列表归纳、符号表征规律等方法，从而促进了学生思维能力的进阶。

（1.浙江省台州市椒江区洪家中心小学

2.浙江省台州市椒江区中山小学）