基于高阶半解析移动脉动源法的船舶波浪增阻数值计算研究

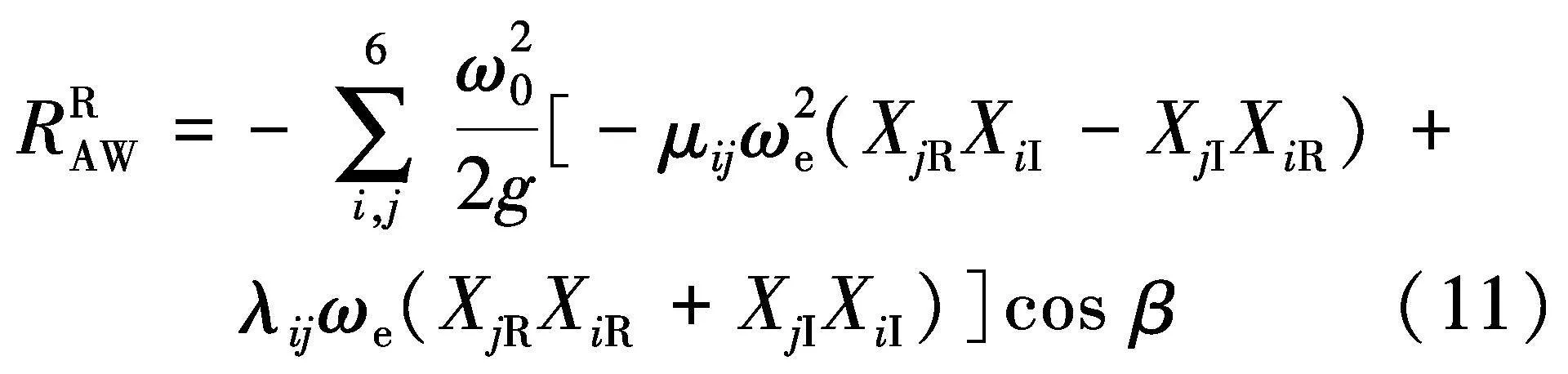
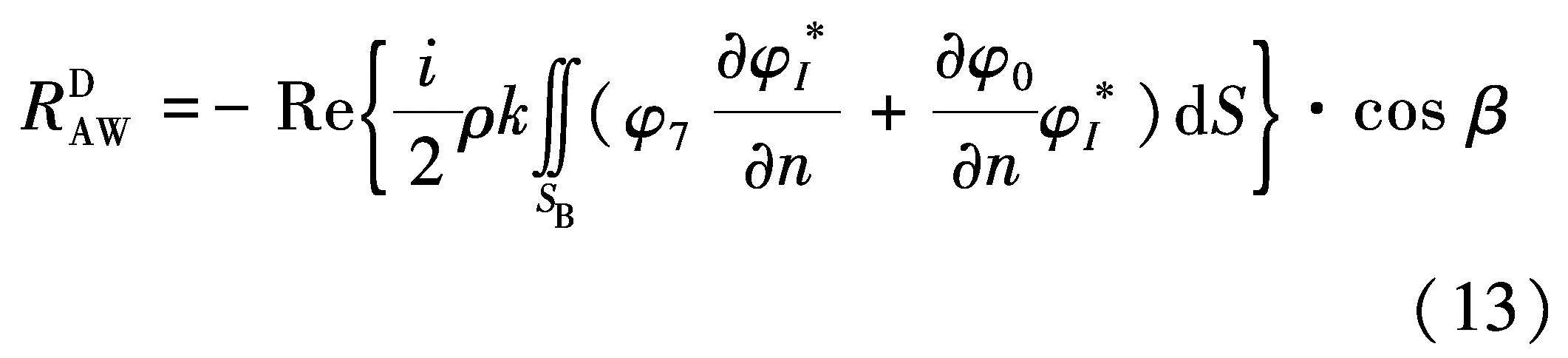
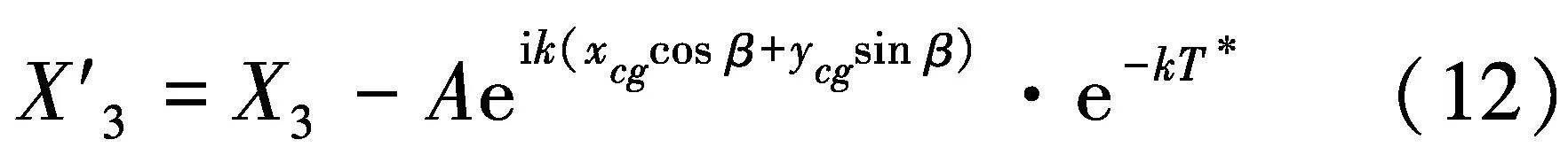
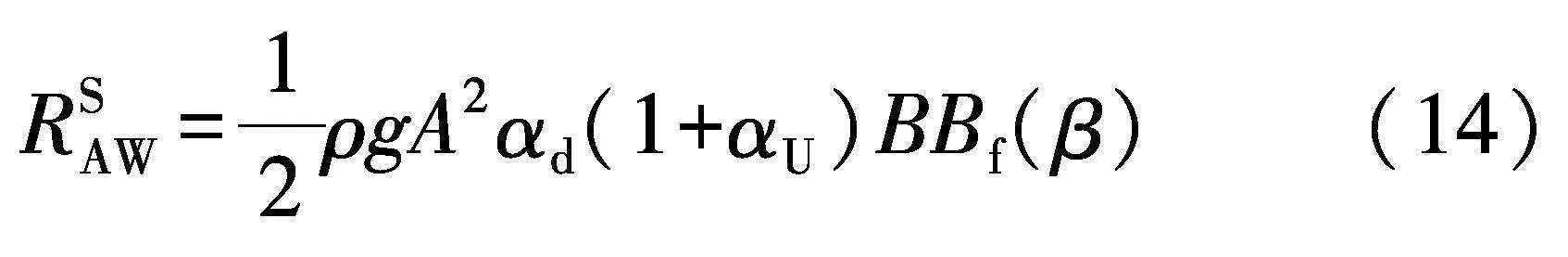
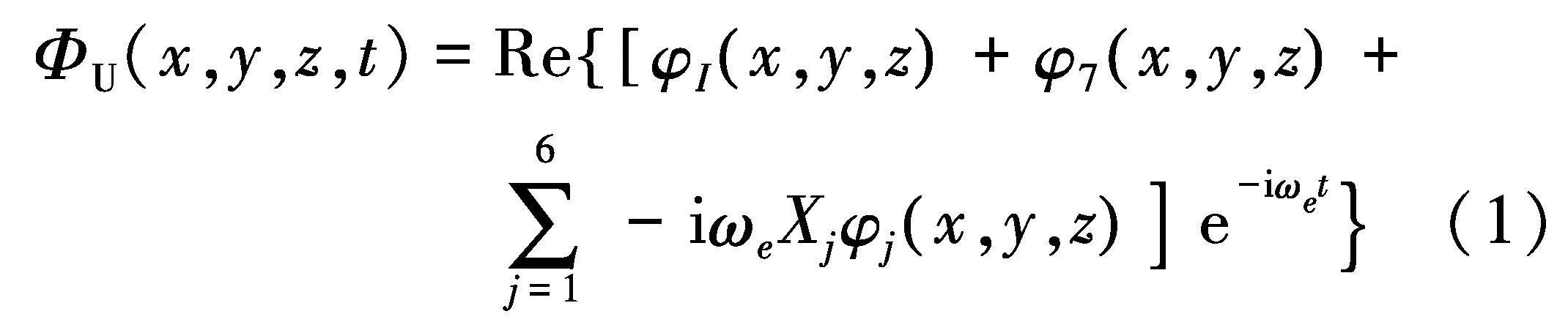
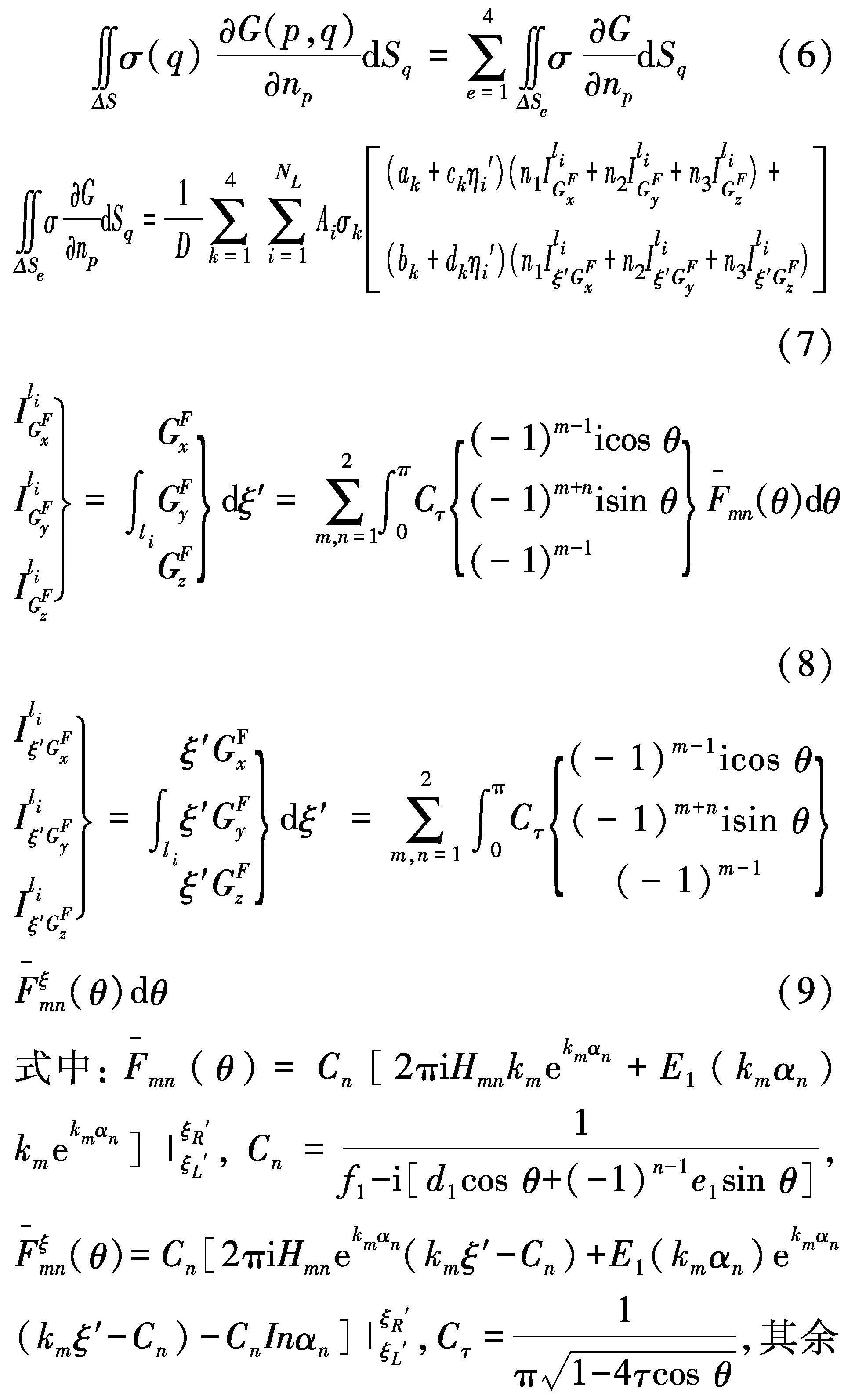
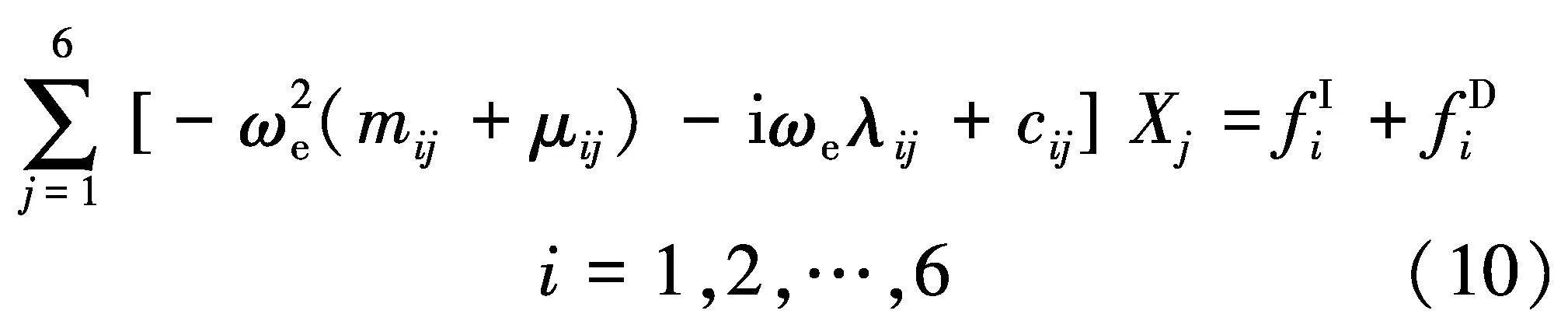
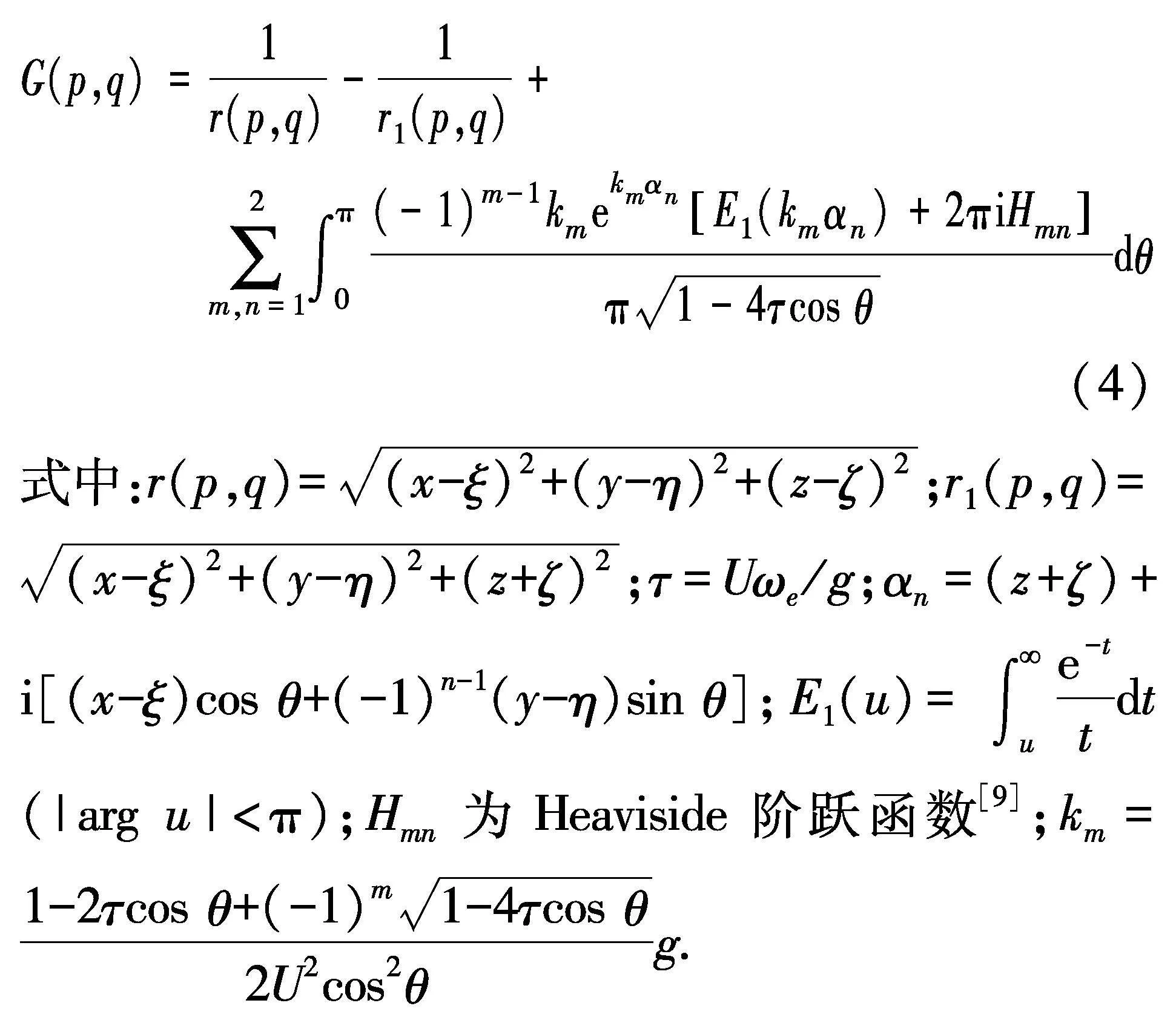
摘 要： 在三维势流理论框架下，以移动脉动源格林函数为核函数构建边界积分方程，采用九节点高阶曲面单元进行离散求解速度势，建立了波浪中航行船舶运动响应和波浪增阻的计算模型.为了避免数值计算的不稳定，积分方程中的影响系数采用了半解析公式进行计算.求解波浪增阻时，采用将辐射能量法、Salvensen法和短波半经验公式相结合的混合法，以便能够在全频率范围内得到令人满意的结果.在此基础上，自主开发数值程序对不同船型在不同频率、航速下的运动响应和波浪增阻进行预报.通过将预报值与试验及其它数值方法的结果进行对比发现，文中方法的数值结果与试验值吻合良好，对于不同船型和工况均有着良好的适用性；相比传统基于数值求积公式的移动脉动源法，高阶半解析移动脉动源法计算更为稳定（尤其对于存在外飘的船型），且由于采用了高阶格式，在共振频率附近的预报精度比常值元法更高.

关键词： 波浪增阻；移动脉动源；高阶；半解析；混合法

中图分类号：U661.32"" 文献标志码：A"""" 文章编号：1673-4807（2024）02-015-08

Numerical study on added resistance of ships advancing in waves byhigher-order semi-analytical translating-pulsating source method

Abstract：Within the framework of three-dimensional potential flow theory， a computational model based on translating-pulsating source Green′s function and 9-node higher-order discretization is established for the motion responses and added resistance of ships advancing in waves. In order to avoid the numerical instability， semi-analytical quadrature formula is derived and employed to evaluate the influence coefficients of the boundary integral equation. And the added resistance is calculated by a combined formula of radiation energy method， Salvensen′s method and semi-empirical method in short waves. Based on the above method， a computer code is developed to investigate the motions and added resistance of various ships at different frequencies and forward speeds. By comparing the predicted results with those of experiment and other numerical methods， it is found that the higher-order semi-analytical translating-pulsating source method can work well for different ship types and working conditions. Besides， the present method appears to be more stable than the translating-pulsating source method based on traditional numerical quadrature formula （especially for the non-wall-sided ship） and more accurate than the constant panel method.

Key words：added resistance， translating-pulsating source， higher order， semi-analytical quadrature， combined method

船舶在海上航行时，不可避免地会遭遇波浪.在波浪的作用下，船舶除了会产生各种摇荡运动之外，受到的阻力相比于静水也会有所增加，这无疑会大大增加船舶的燃料消耗、影响其保持航速的能力等.因此，寻求合理而实用的数值方法对航行船舶的波浪增阻进行预报研究，对船舶的设计、使用等具有重要意义.势流方法因其高效并能保有足够的精度，在波浪增阻问题中应用广泛.最简单的势流方法是切片法，早期大多数波浪增阻计算方法都是基于此来表达的[1-2].但是该方法在计算中采用的高频、低速、船体细长等假定，限制了其进一步的发展与应用.近年来出现了大量关于三维势流方法的研究工作，这些方法根据构建积分方程时采用的核函数的不同，通常可以分为Rankine源法和自由面格林函数法两类.Rankine源法的优点在于可以适用于不同形式的边界条件，考虑非线性、浅水效应等，但在有航速水动力分析中，它存在着离散量大、难以处理Brard数较小时的辐射条件等缺陷限.

相对而言，自由面格林函数法由于选择的格林函数自动满足自由面和辐射条件，只需在物面布源，离散量较小.利用该方法研究船-波相互作用问题最为关键的一点在于格林函数的计算.针对无航速自由面格林函数（又称脉动源格林函数），文献[3]做了大量的研究工作，提出了快速高效的数值算法，基于此开发了比较实用的无航速波浪与结构物相互作用问题的求解软件；在此基础上，文献[4-5]基于脉动源格林函数，通过航速修正考虑航速效应，分别采用不同的远场公式对船舶的波浪增阻和横向二阶力进行了计算.然而，这类方法只适用于航速较低的工况，对中高航速并不能得到令人满意的数值结果.为了充分考虑航速效应，应该采用有航速自由面格林函数（又称移动脉动源格林函数）.近年来，在有航速自由面格林函数及其面积分数值计算方法方面的研究工作[6-10]，在一定程度上促进了移动脉动源法的发展.但从实际工程意义角度来说，该方法距离真正应用于有航速船舶水动力分析仍然任重而道远.尤其是对存在外飘的中高速船，格林函数在近自由面附近的剧烈振荡特性[11]，使得移动脉动源法很难获得稳定的数值结果.鉴于此，目前很少有学者基于该方法对船舶波浪增阻问题进行研究.文献[12]曾尝试基于移动脉动源法的水动力结果，分别采用辐射能量法和Salvesen法[13]对由船舶摇荡运动以及绕射作用引起的波浪增阻进行了计算.但受限于格林函数积分在自由面附近的不稳定性，数值格式采用的是基于常值单元离散的低阶格式，这是少有的基于移动脉动源法对波浪增阻的研究.

文中针对波浪中航行的船舶，基于移动脉动源格林函数，建立了一种计算波浪增阻的高阶半解析方法.该方法利用九节点高阶曲面单元离散以移动脉动源格林函数为核函数的边界积分方程，分别采用解析公式和Gauss-Legendre求积公式计算影响系数沿水平和垂直方向的积分，以避免格林函数沿水平方向的剧烈振荡所引起的数值计算不稳定.求解波浪增阻时，为了在全频率范围内得到令人满意的结果，采用了将辐射能量法（用于计算辐射增阻）、Salvensen法（用于计算绕射增阻）和短波半经验公式相结合的混合法.在此基础上，采用Fortran自主开发数值程序，对不同船型（包括数学船型modified Wigley和集装箱船S175）在规则波中以不同航速航行时的运动和波浪增阻进行数值计算，并将结果与试验和其它数值方法的结果进行对比分析.

1 求解速度势的高阶半解析移动脉动源法

1.1 速度势与边界积分方程

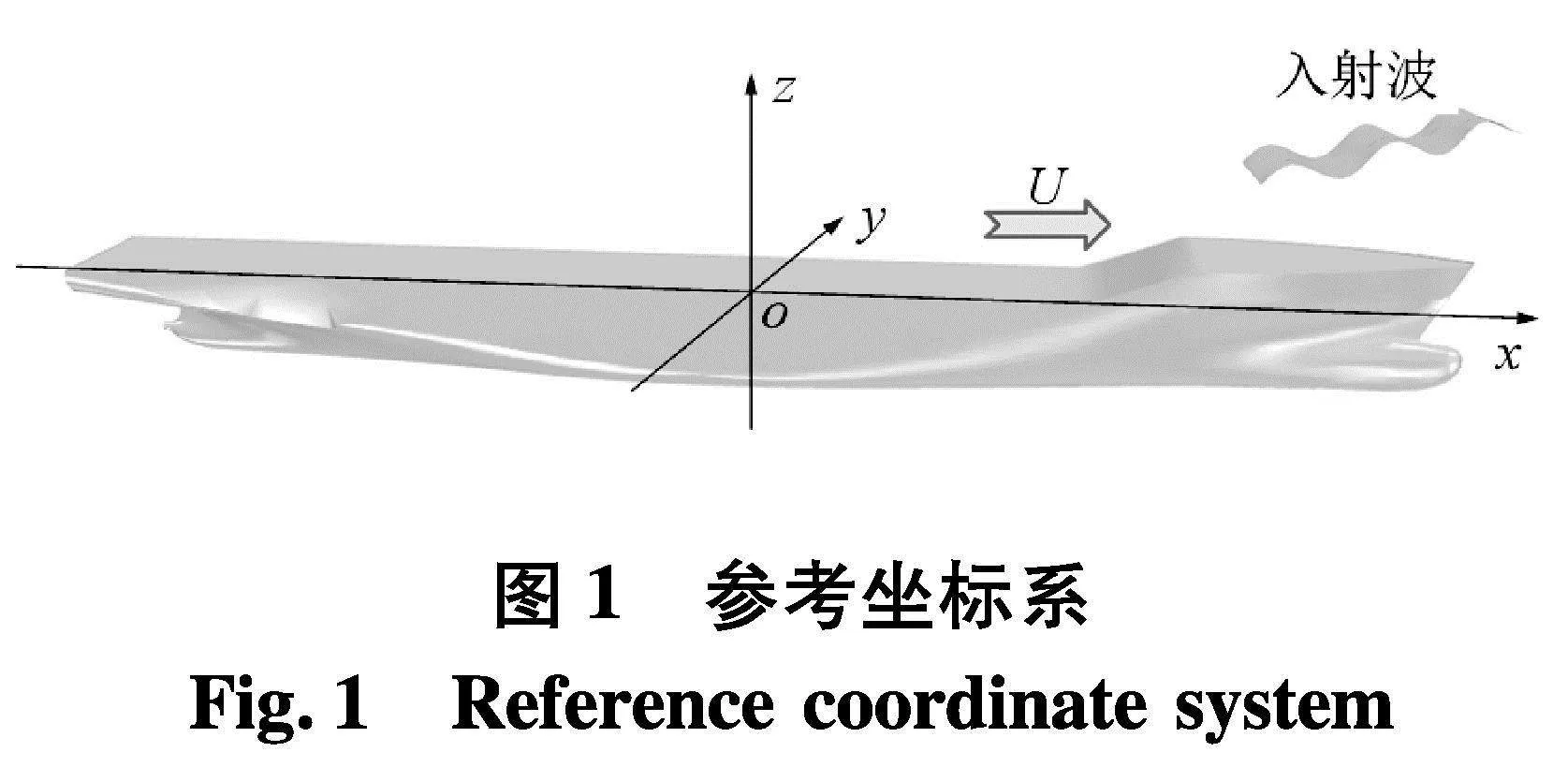
在势流理论框架下，波浪中航行船舶的水动力力问题可以通过引入速度势函数来研究.为了便于求解速度势，建立以船舶平均速度U运动的参考坐标系o-xyz（图1）.

该坐标系的原点o位于船舶重心正上方的平均静水面，x轴与船舶前进方向相同，z轴竖直向上.当入射波是微幅波，船舶摇荡运动幅值不大时，流场的非定常扰动势可以分解为：

式中：px，y，z代表场点；qξ，η，ζ代表源点；σp和σq分别为p和q点处的源强；SB和CW分别船体的平均湿表面和水线；n1为单位外法线矢量n沿x轴的分量；G（p，q）为满足自由面条件和辐射条件的移动脉动源格林函数，Havelock型单积分为[15]：

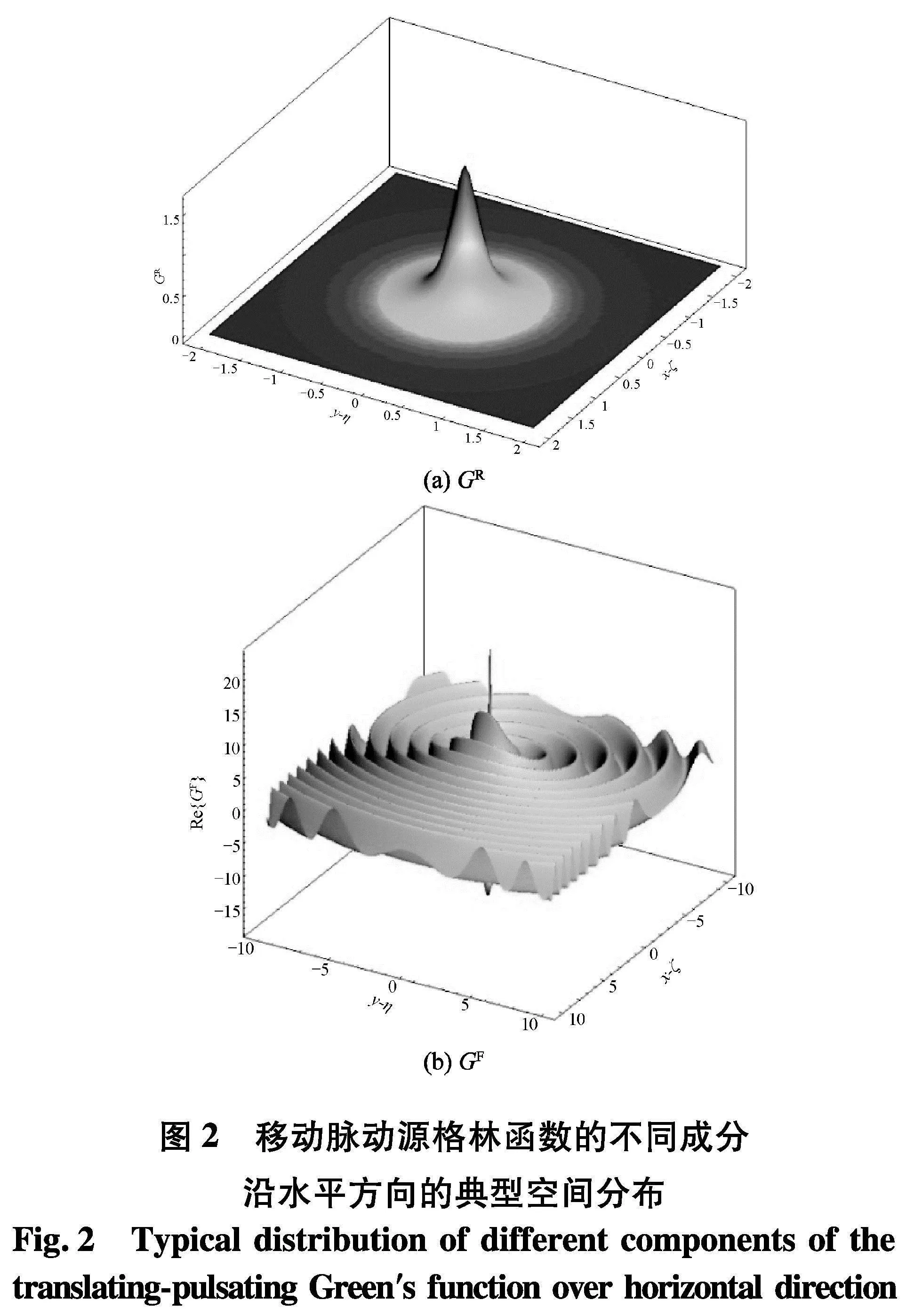
文中将移动脉动源格林函数Havelock型表达式中的前两项记为GR（p，q），最后一项记为GF（p，q）.从表达式可以看出，GR只取决于场、源点的相对位置，而GF则还与航速等物理量相关.图2为GR和GF沿水平方向的典型空间分布.可以看出，GR是一个平滑变化的函数，而航速相关部分GF沿水平方向则呈现出剧烈的振荡特性.

1.2 高阶面元离散及影响系数计算

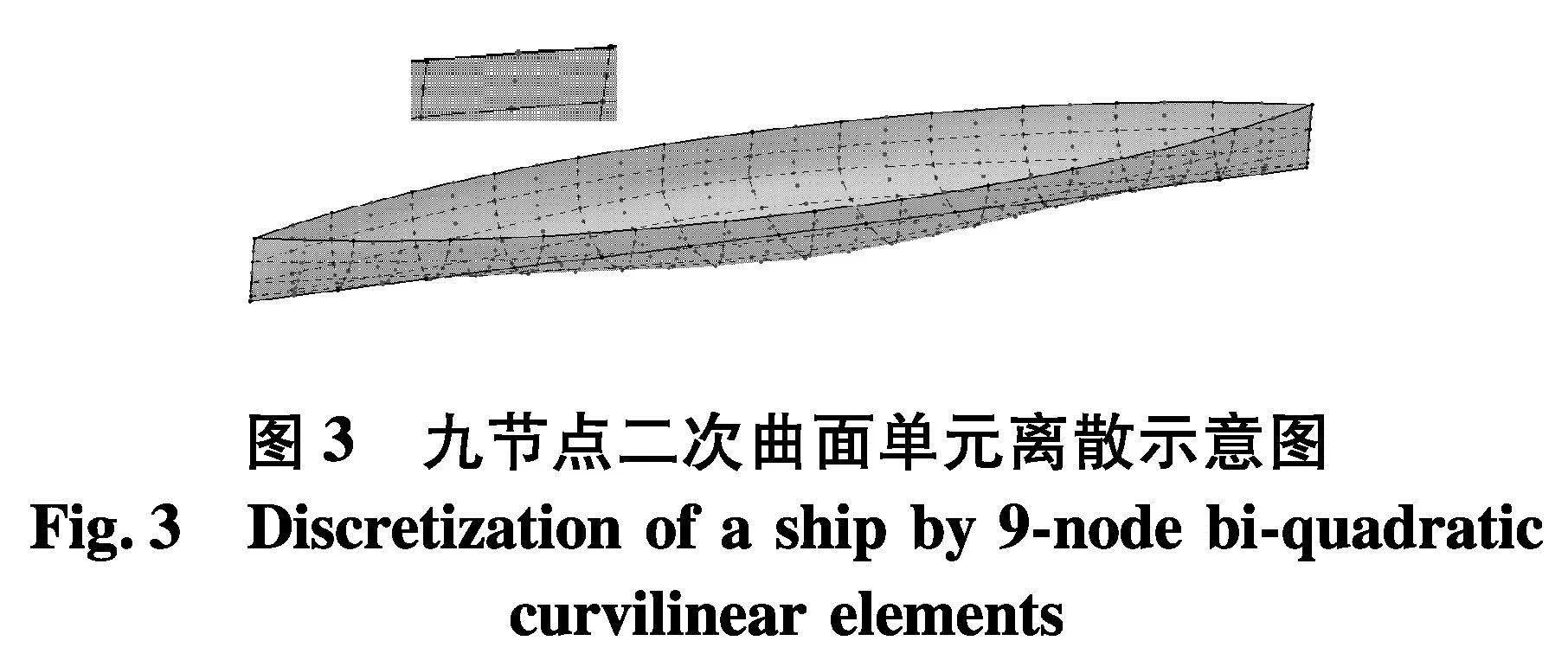
边界积分方程式（3）需要采用面元对边界进行离散转化为代数方程组后，才可以进行数值求解.最常用的离散面元是三角形或者四边形常值单元.在常值元中，各未知物理量被假定为常值，因而比较简单易于实现.但是它存在离散量大、单元间变量不连续等固有缺陷.为了克服这些问题，文中采用九节点二次曲面单元对船体表面进行离散（图3中的点代表控制点）.该单元中任意一点处的变量值可以利用控制点处的值插值获得[16].

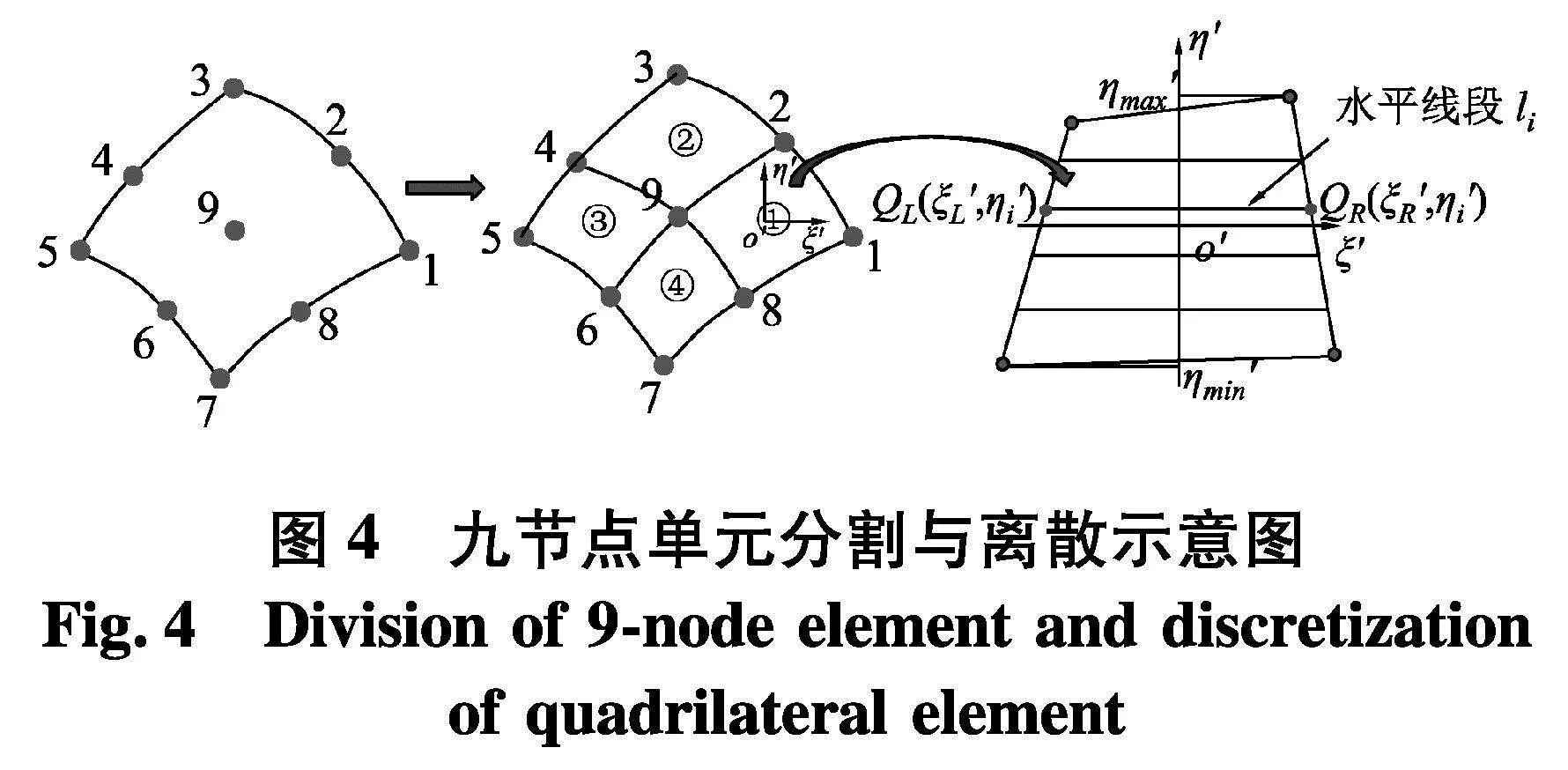
理论上，标准正方形单元上的积分可以直接采用Gauss-Legendre求积公式进行计算.然而，格林函数航速相关部分GF沿水平方向的剧烈振荡特性（图2）使得很难采用简单的数值积分方法获得关于其的稳定积分结果[8].为了克服该问题，文中在计算与GF法向导数相关的面积分时，首先将图3中的九节点单元分割为4个四节点单元（图4）.然后采用不同的积分策略对四节点单元上的积分进行计算：垂向仍采用数值积分方法，而水平方向则推导了解析积分公式进行计算，以避免GF沿水平方向剧烈振荡所导致的积分计算不稳定问题.具体计算为：

系数的表达式见文献[10].

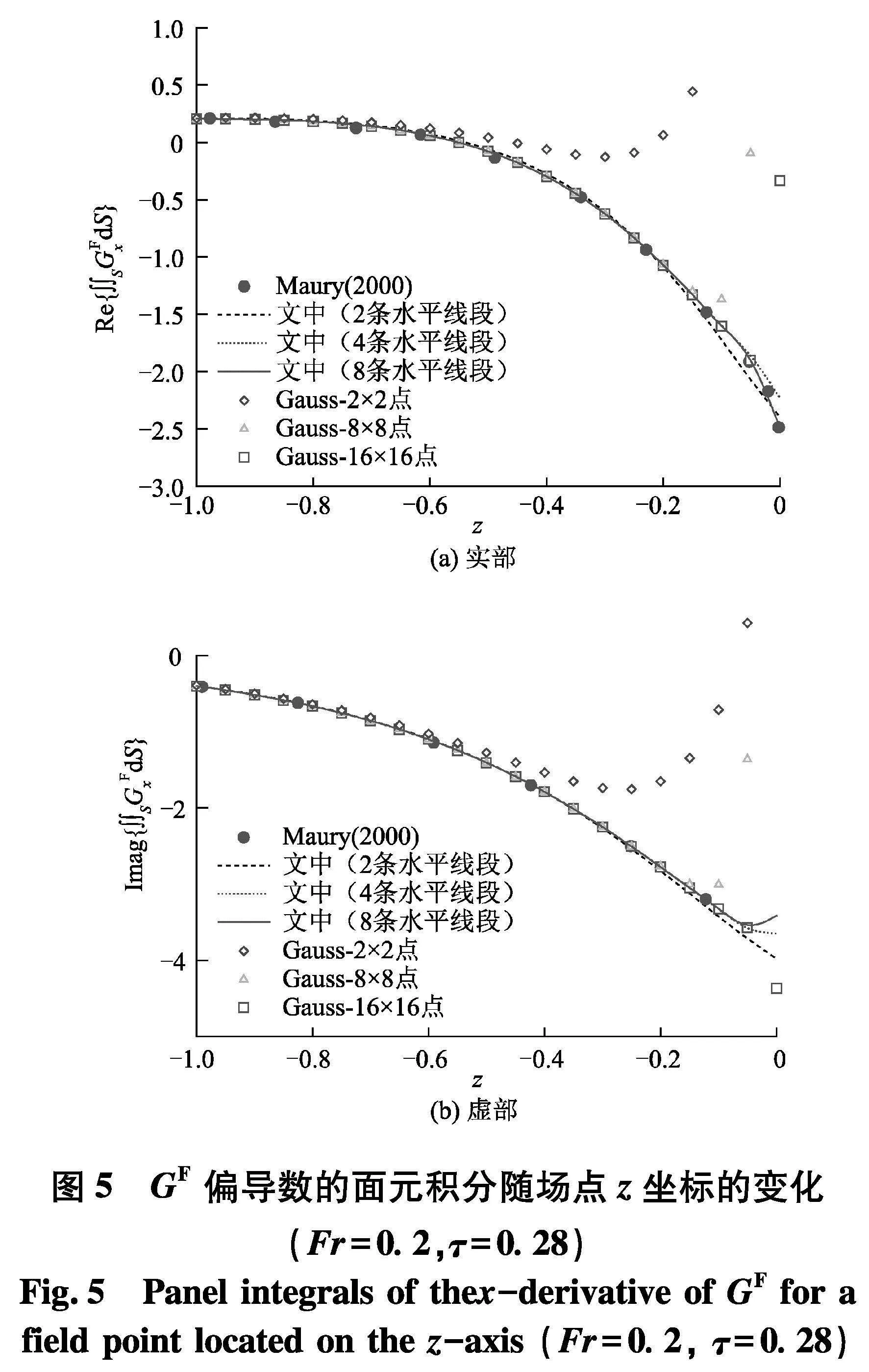
图5为采用上述半解析方法计算单位正方形（其形心位于（0， 0， -0.51）、法向沿y轴）上GF偏导数面积分的结果与传统Gauss-Legendre求积公式计算结果的对比.可以看出，当z远小于0（即场点远离自由面）时，只要单元中布置的高斯点数目足够多，传统的Gauss-Legendre求积公式也可以获得令人满意的结果；但是当z趋于0时，即使在单元中布置了16×16个高斯点，Gauss-Legendre求积公式的结果仍然与理论解[18]存在偏差，而文中的半解析方法则可以在离散水平线段数目达到8时获得足够的精度.

在采用九节点高阶面元对船体表面进行离散，并利用文中建立的公式对边界积分方程式（3）中与GR和GF相关的面元积分进行计算后，便可求出边界上的源强，进而得到流场速度势.

2 运动响应与波浪增阻计算方法

将入射势I和求得的辐射势j（j=1， 2，...， 6）、绕射势7代入水动力计算公式[19]，便可计算得到作用在船体上的波浪激励力和水动力系数.在此基础上，求解频域运动方程式（10）[20]，便可得到船舶的运动响应Xj.

式中：mij为船舶质量惯性力系数；cij为恢复力系数；μij和λij分别为附加质量和阻尼系数；fIi和fDi分别为入射力和绕射力的复数幅值.

波浪中航行船舶除了会产生各种摇荡运动之外，受到的阻力相比于静水中也会有所增加.这些附加阻力会增加船舶的燃料消耗，影响船舶保持航速的能力.因此，准确预报波浪增阻，对船舶的设计和使用至关重要.为了便于计算和分析，波浪增阻通常可以被分为辐射增阻和绕射增阻两部分.

辐射增阻的计算公式可以根据能量守恒原理得到[21]：

式中：RRAW代表辐射增阻；XiR和XiI分别代表Xi的实部和虚部，XjR和XjI分别代表Xj的实部和虚部.Xi（或Xj）原则上可通过求解频域运动方程式（10）获得，但是这个值是相对于船舶在静水中的平衡位置而言的.为了考虑船体周围波面变化的影响，文中参照文献[21]中的做法对船舶垂荡运动幅值加以修正：

式中：X′3为修正后的垂荡运动幅值；xcg和ycg分别代表重心处的x和y坐标；T*为船舶平均吃水，近似等于Aw（和Aw分别为船舶的排水体积和水线面面积）.

至于绕射增阻，通过移除Salvesen平均二阶力计算公式[13]中与辐射势相关项，保留其中与绕射势相关的项来计算，具体表达式为：

式中：RDAW代表绕射增阻；φ*I为入射势I的共轭复数.

将由式（11、13）分别计算得到的辐射增阻和绕射增阻相加，便可得到船舶在波浪中航行时所受到的总的波浪增阻.然而需要注意的是，上述计算公式均是在线性势流理论框架内建立的，当入射波长较短时，并不适用.为了弥补它们的不足，日本海上技术安全研究所（NMRI）提出了一种短波增阻半经验计算公式为[22]：

式中：RSAW代表短波时的波浪增阻；B为船宽；系数αd，αU和Bf的表达式见文献[22].

前面的辐射增阻、绕射增阻公式（11、13）只适用于波长较长的工况，而半经验公式（14）只适用于波长较短的工况.为了克服其局限性，文中参考文献[23]的做法，提出将长波、短波增阻公式相结合的混合计算方法，以便在全频率范围均能够获得准确的波浪增阻预报结果.

RAW=（1－αd）（RRAW+RDAW）+αdRSAW（15）

3 数值结果与分析

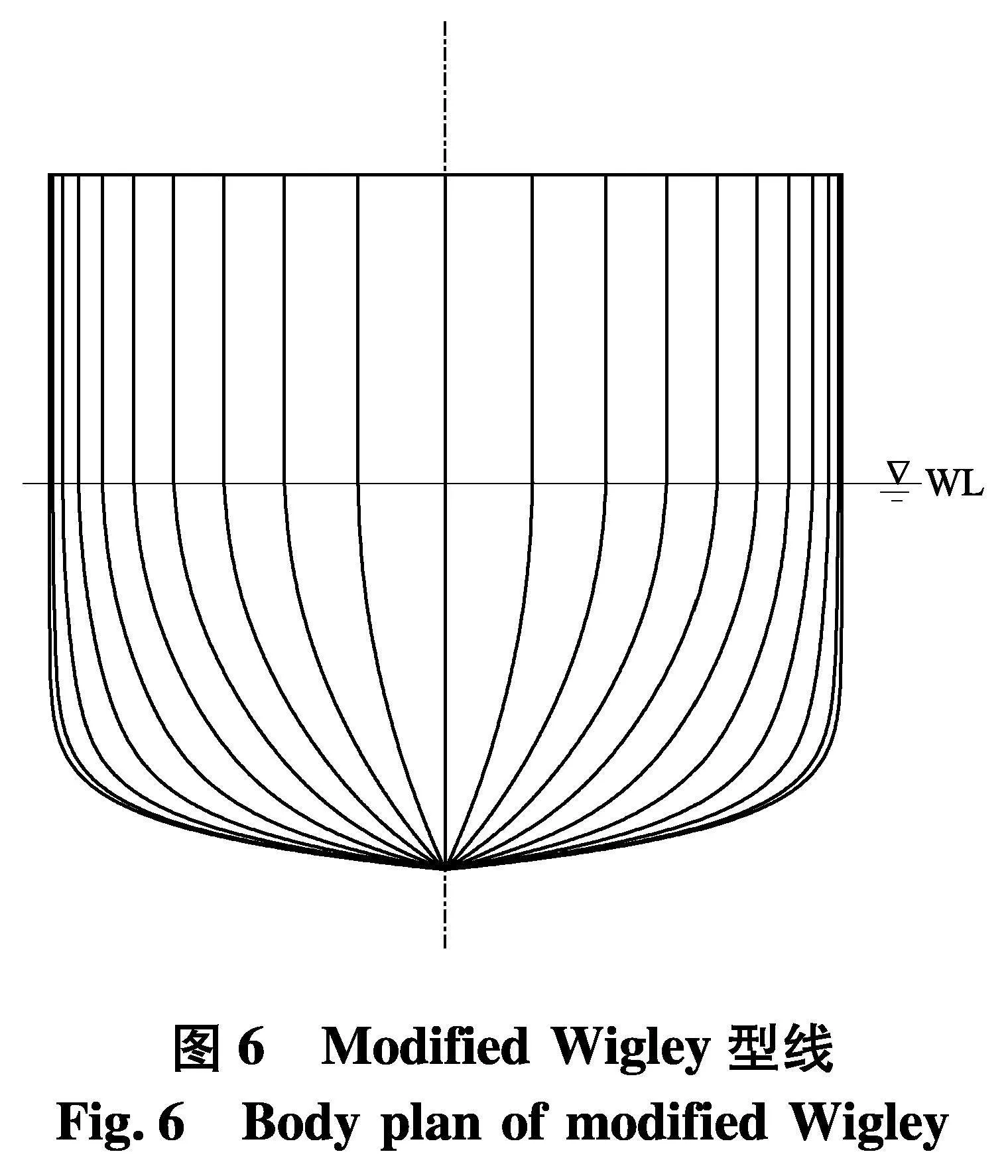
基于上述理论和方法，采用Fortran开发相应的数值计算程序.为了对程序进行验证，首先以文献[23]为研究对象，计算船舶运动响应和波浪增阻，并与试验和其它数值方法的预报结果进行对比分析.Modified Wigley是一种数学船型，船长L为2 m，船宽B为0.3 m，吃水D为0.125 m.图6为modified Wigley船的型线图，从图中可以看出，modified Wigley船是一种直壁型船，横剖线在水线处与自由面垂直.

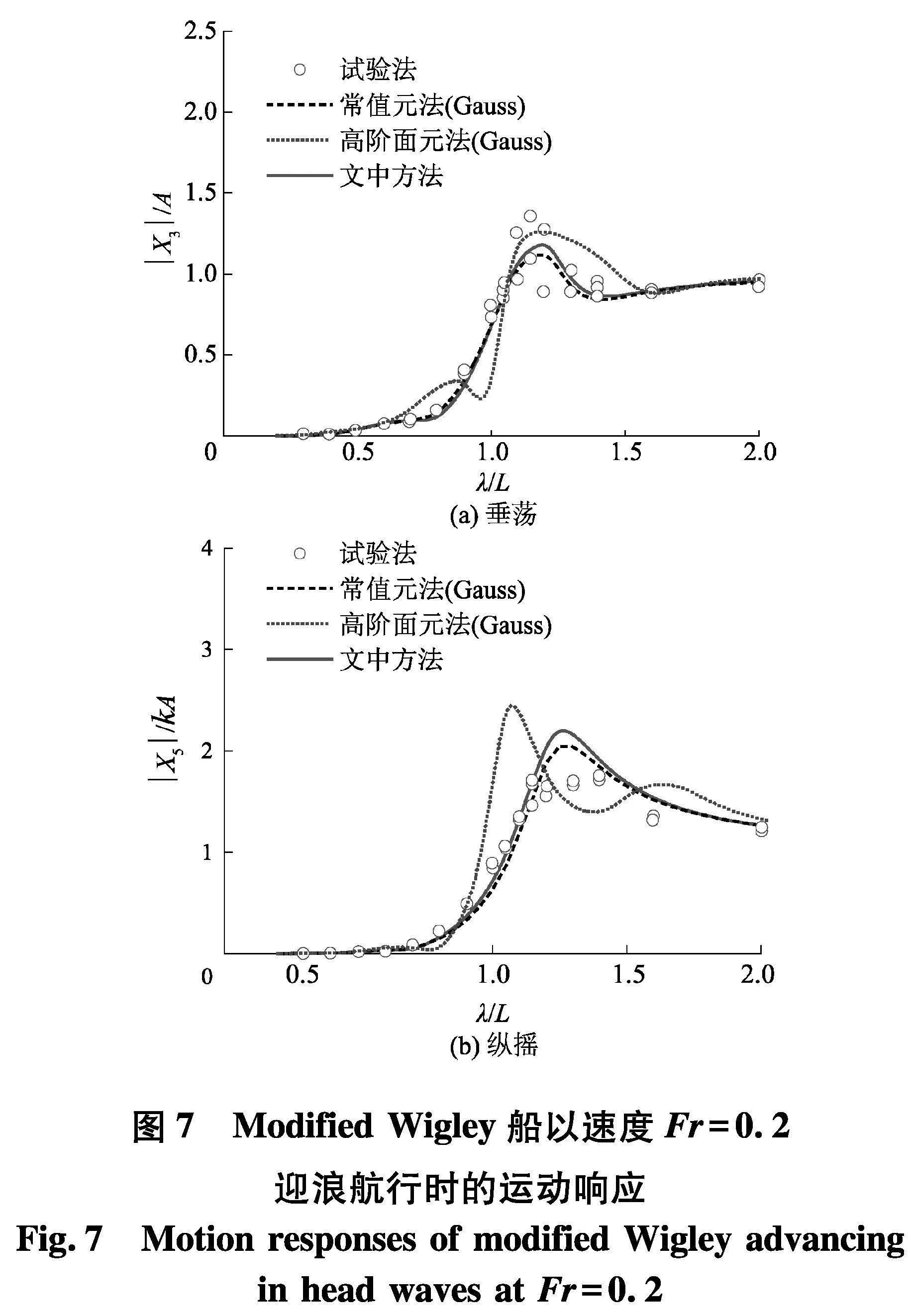
图7为modified Wigley以速度Fr=0.2在不同波长（波长λ船长L比范围为0.2～2.0，间隔为0.1）的规则波中迎浪航行时的垂荡和纵摇运动RAO（response amplitude operator）.为了进行对比分析，图中除了文中的计算结果，还包括了试验[24]、基于Gauss-Legendre求积公式的常值元法和高阶面元法的结果.从图中的结果可以看出，常值元法和文中建立的高阶半解析移动脉动源法的计算结果差异不大（文中高阶方法得到的垂荡运动响应在峰值附近的精度略高），并且总的来说均与试验值吻合良好（这主要是因为modified Wigley船是一种简单的数值船型，常值元离散也可以获得比较好的精度）.但是由于船体在采用高阶面元进行离散时，最上面一层的控制点位于自由面，而传统数值积分法在场、源点接近自由面时无法获得精确的格林函数面积分值（图5），基于Gauss-Legendre求积公式高阶面元法计算得到的运动响应呈现出明显的振荡特性.

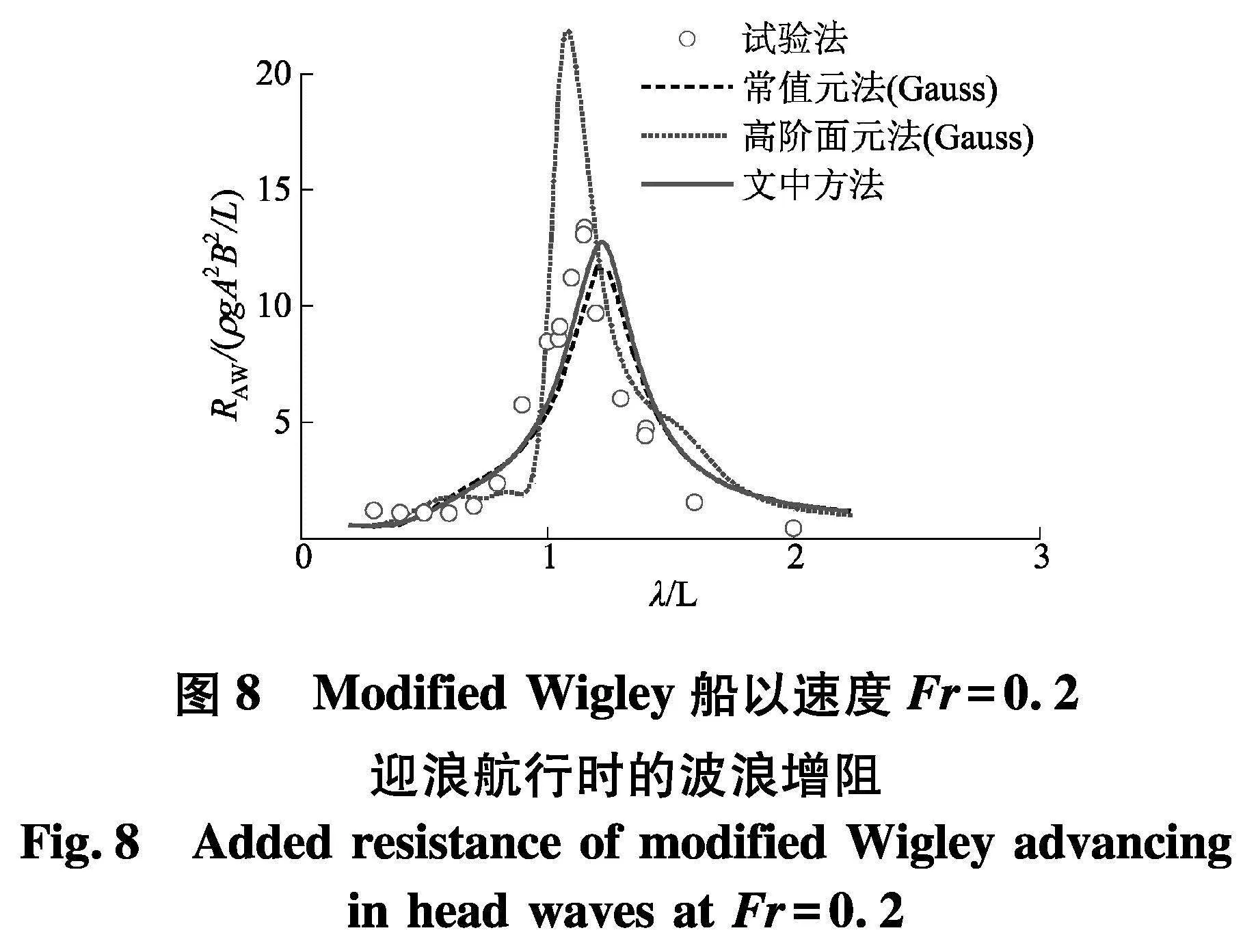
图8为modified Wigley在Fr=0.2时的波浪增阻.可以看出，类似于前面运动响应的结果，基于常值元法和文中高阶半解析移动脉动源法计算得到波浪增阻总的来说也与试验值吻合良好（其中高阶方法的精度在共振频率附近更高）.而传统基于Gauss-Legendre求积公式的高阶面元法由于无法获得稳定的运动响应结果，计算出的波浪增阻也呈现出明显的振荡特性.

以上结果是在处理器为AMD EPYC 7H12（主频为2.6 GHz）工作站上采用40个线程并行计算获得的，平均每个频率的计算时间在17.6 s左右.可以看出，文中程序的计算效率较高，能够满足工程需求.

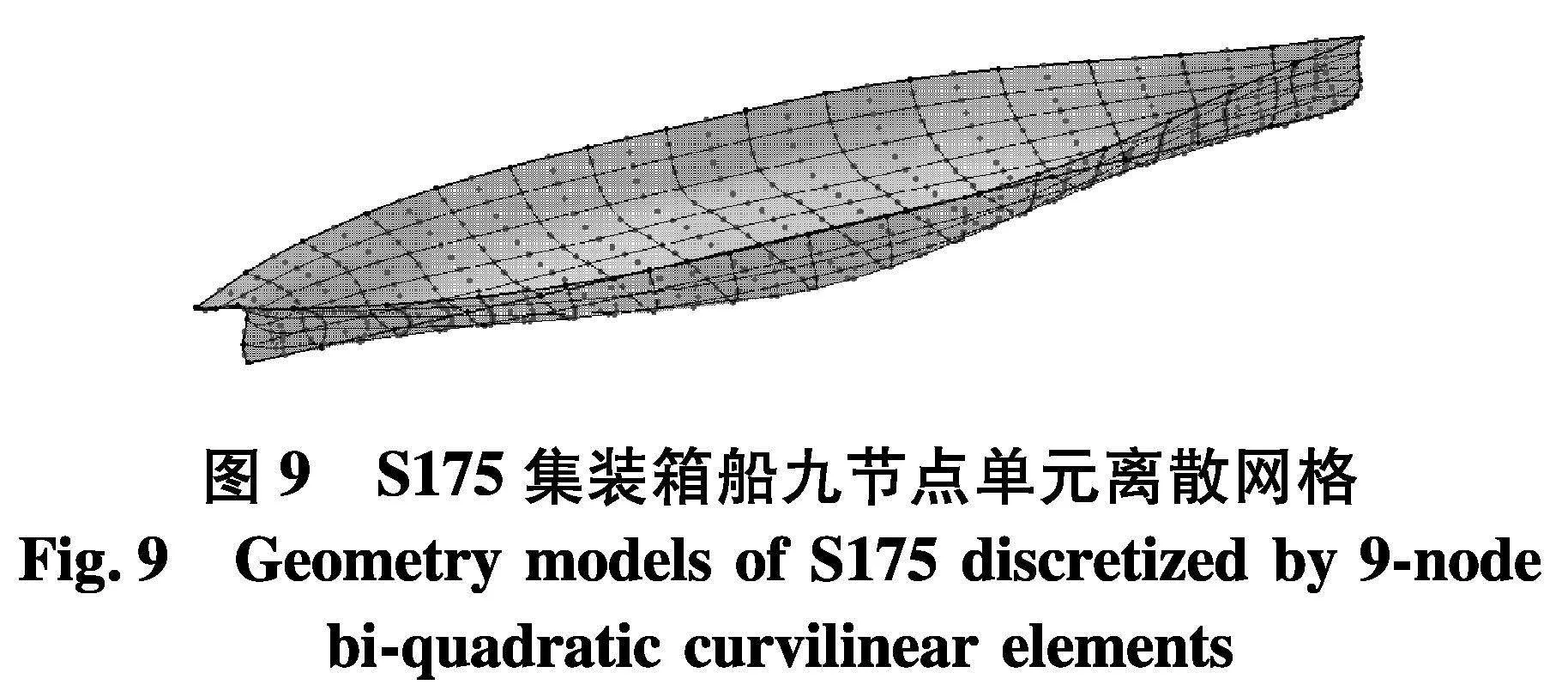
前面对modified Wigley船的计算分析表明，文中建立的高阶半解析移动脉动源法以及基于此的波浪增阻方法对于简单数学船型可以获得令人满意的运动响应和波浪增阻预报结果.为了进一步验证该方法在实际船舶中的适用性，将进一步对S175集装箱船的波浪增阻进行计算.S175是ITTC标准船模，船长L为175 m，船宽B为25.4 m，吃水D为9.5 m，排水量Δ为24 742 t，重心位于船尾部分且距离船中2.48 m，重心高度KG为9.52 m，纵摇方向转动惯量为43 644 888 t·m2.图9为S175船的九节点单元离散网格，可以看出，不同于modified Wigley，S175在自由面附近存在一定的外飘.

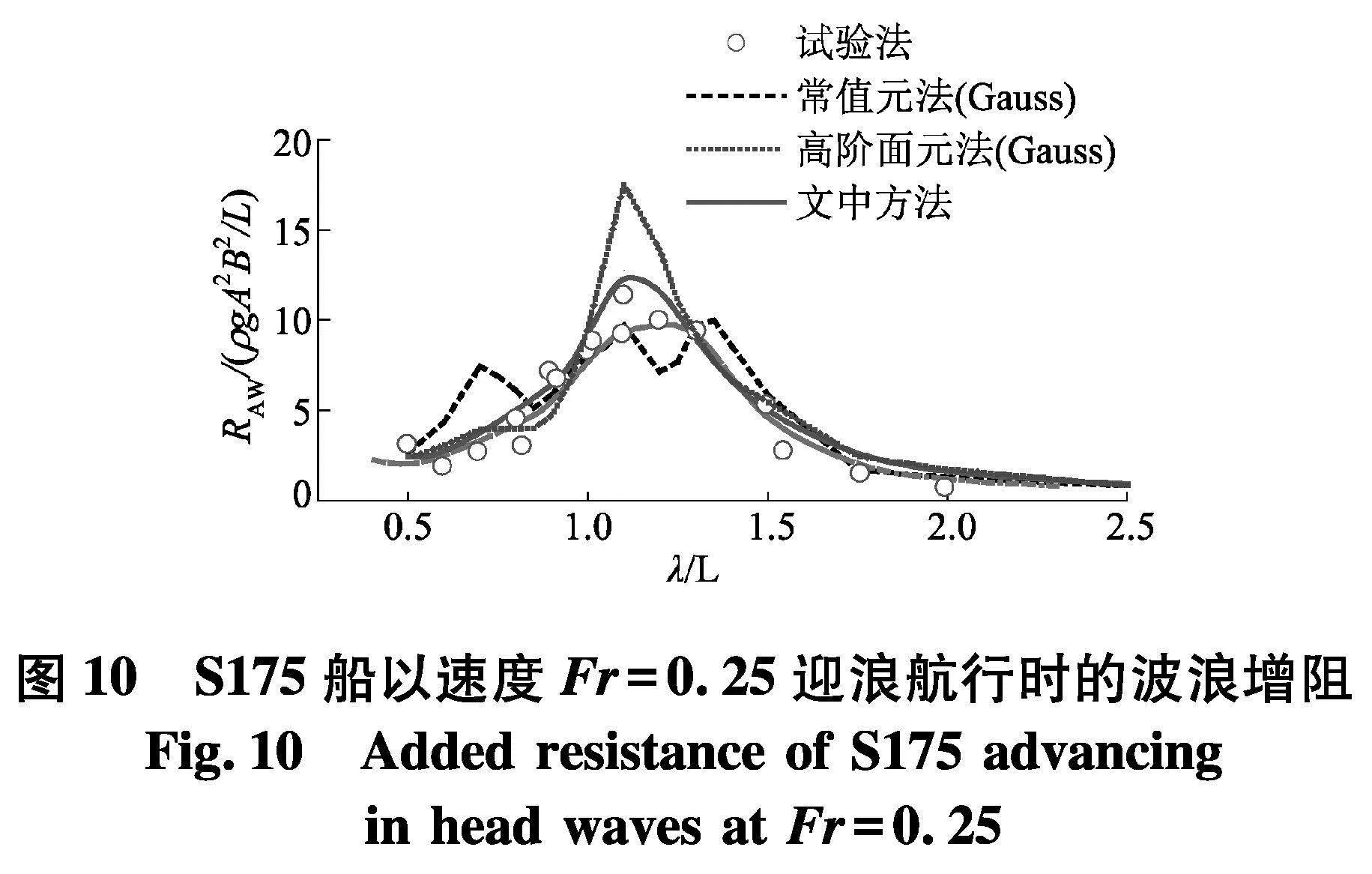
图10为S175以航速Fr=0.25在规则波中迎浪航行时，波浪增阻的计算值和试验数据[25-26]的对比.计算的波长船长比范围为0.5～2.5，间隔为0.1.除了文中高阶半解析方法的结果，图中数值结果还包括基于半解析积分公式的常值元法[12]、基于Gauss-Legendre求积公式的常值元法和高阶面元法的计算值.从图中结果可以看出，基于Gauss-Legendre求积公式的常值元法和高阶面元法计算得到的波浪增阻比其他两种数值方法的结果更为振荡.这主要是因为S175船在水线附近存在外飘，在外飘处，即使采用常值元进行离散，它的控制点距离自由面也非常接近，从而导致很难采用数值积分公式获得准确的格林函数面积分值.对比基于半解析积分公式的常值元法和文中方法计算得到的波浪增阻可以发现，虽然前者也可以获得稳定并且总体令人满意的结果，但是由于常值元离散的固有缺陷，它的计算精度在共振频率附近明显不如文中的高阶方法.

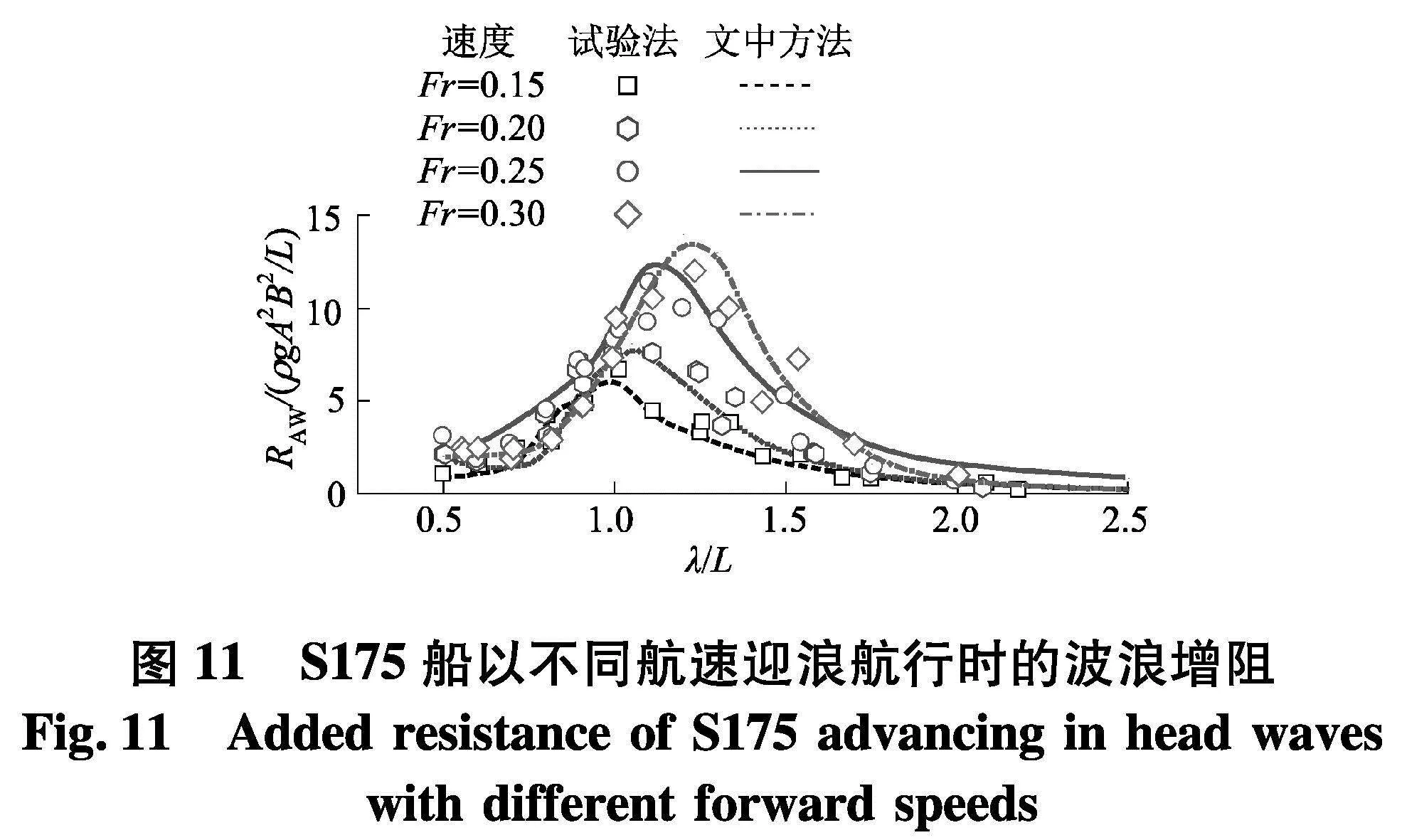
基于文中建立的高阶半解析移动脉动源法，进一步对S175船以速度Fr=0.15， 0.20， 0.30迎浪航行时的波浪增阻进行计算，结果如图11.从图中可以看出，数值结果与试验值吻合良好，表明本文方法适用于不同航速下船舶波浪增阻的预报.此外，对比图中不同航速下的结果可以发现，S175船受到的波浪增阻存在明显的航速效应，它的峰值及其对应的无因次波长均会随着航速的增大而增大.

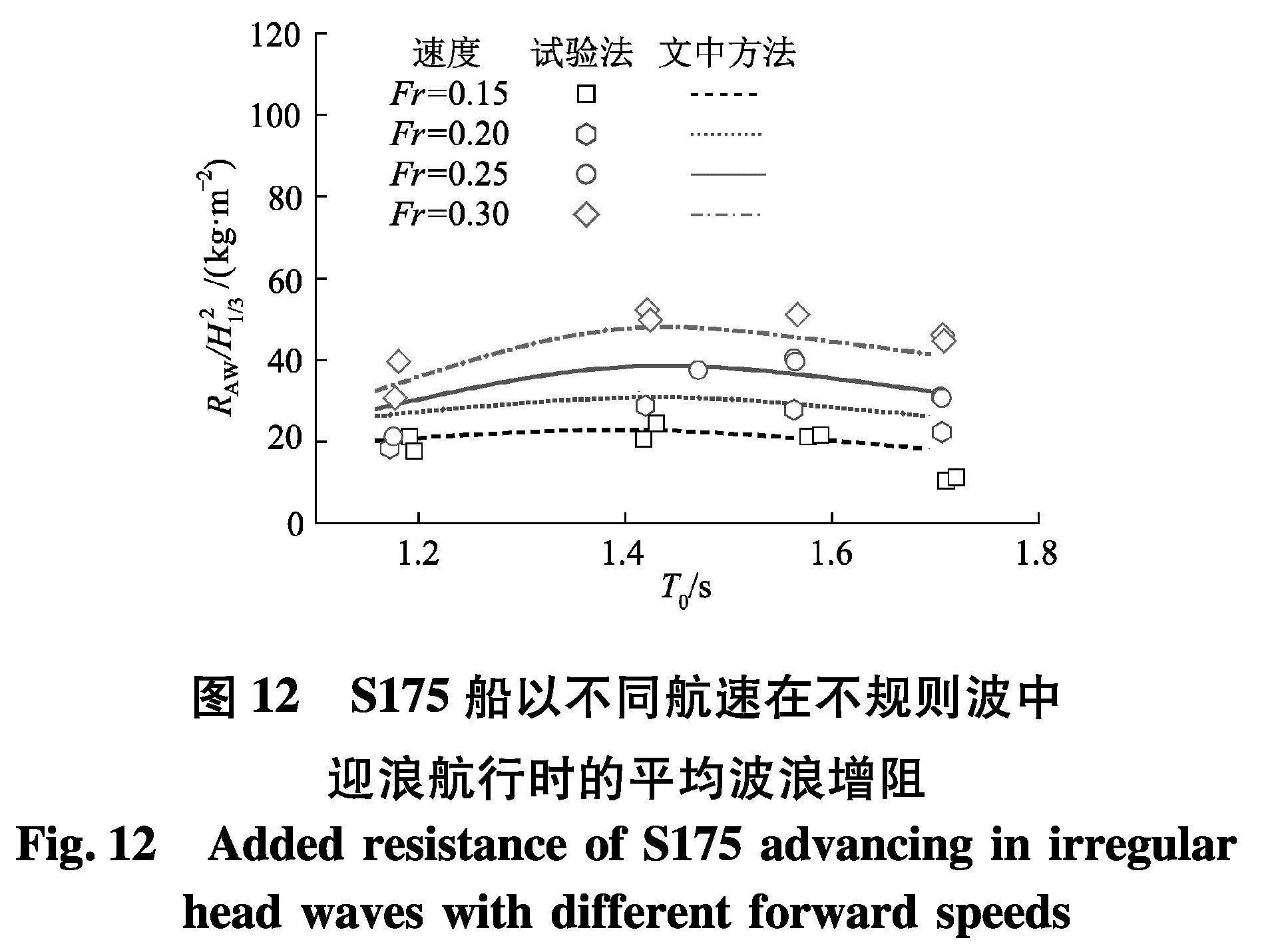
为了进一步分析文中方法的可行性和可靠性，在前面规则波中波浪增阻计算的基础上，下面进一步采用谱分析方法对S175在实际海况中航行时的波浪增阻进行预报.数值计算采用与Nakamura 和文献[26]相同的波浪谱，有义波高H1/3分别取10.78、9.99、10.56、10.04 cm，相应的平均周期T0分别取1.159、1.413、1.562、1.694 s.图12为S175以速度Fr=0.15、0.20、0.30分别在4种海况中迎浪航行时的波浪增阻平均值随平均周期T0的变化.从图中可以看出，虽然部分航速下的数值结果在平均周期较短时存在一定的误差（这可能是试验本身的误差或者是线性叠加的谱分析方法与实际物理情况之间存在差别导致），但总的来说预报值与试验值吻合良好，在工程可以接受的范围内.

4 结论

（1） 与传统Gauss-Legendre求积公式相比，本文建立的半解析积分方法由于在计算与移动脉动源格林函数航速相关部分GF相关的面积分时，对沿水平方向的积分采用了解析计算公式，从而避免了GF的剧烈振荡特性所导致的自由面附近边界积分方程影响系数计算不准确问题；

（2） 在波浪中航行船舶的运动响应和波浪增阻数值计算中，文中高阶半解析移动脉动源法比相应的基于Gauss-Legendre求积公式的面元法更为稳定（尤其是对于存在外飘的船型），比常值元法的预报精度更高；

（3） 无论是简单的数学船型Modified Wigley，还是集装箱船S175，基于高阶半解析移动脉动源法计算得到的不同航速下的波浪增阻结果均与试验值吻合良好，表明本文建立的数值方法在波浪引起的船舶阻力增加预报中，对于不同船型、不同航速均有广泛的适用性.

参考文献（References）

［1］ GERRITSMA J， BEUKELMAN W. Analysis of the resistance increase in waves of a fast cargo ship [J]. International Shipbuilding Progress， 1972， 19（217）： 285-293.

[2] SALVESEN N. Added resistance of ships in waves[J]. Journal of Hydronautics， 2012， 12（1）： 24-34.

[3] NEWMAN J N. Algorithms for the free-surface Green function [J]. Journal of Engineering Mathematics， 1985， 19（1）： 57-67.

[4] PAPANIKOLAOU A， ZARAPHONITIS G. On an improved method for the evaluation of second-order motions and loads on 3D floating bodies in waves [J]. Ship Technology Research， 1987， 34： 170-211.

[5] FANG M C， CHEN G R. On the nonlinear hydrodynamic forces for a ship advancing in waves [J]. Ocean Engineering， 2006， 33（16）： 2119-2134.

[6] IWASHITA H， OHKUSU M. Hydrodynamic forces on a ship moving with forward speed in waves [J]. Journal of the Society of Naval Architects of Japan， 1989，166： 187-205.

[7] MAURY C， DELHOMMEAU G， BA M， et al. Comparison between numerical computations and experiments for seakeeping on ship models with forward speed[J]. Journal of Ship Research， 2003， 47（4）： 347-364.

[8] YAO C B， DONG W C. Study on fast integration method for Bessho form translating pulsating source Green′s function distributing on a panel [J]. Ocean Engineering， 2014， 89： 10-20.

[9] HONG L， ZHU R C， MIAO G P， et al. Study on Havelock form translating pulsating source Green′s function distributing on horizontal line segments and its applications [J]. Ocean Engineering， 2016， 124： 306-323.

[10] YANG Y T， ZHU R C， HONG L， et al. A semi-analytical high-order translating-pulsating source method for forward-speed ship motions [J]. Ocean Engineering， 2019， 182： 627-644.

[11] CHEN X B. Highly oscillatory properties of unsteady ship waves [J]. Journal of Mechanical Engineering Science， 2000， 214（6）：813-823.

[12] HONG L， ZHU R C， MIAO G P， et al. An investigation into added resistance of vessels advancing in waves [J]. Ocean Engineering， 2016， 123： 238-248.

[13] SALVESEN N. Second-order steady-state forces and moments on surface ships in oblique regular waves[C]∥International Symposium on Dynamics of Marine Vehicles and Structures in Waves. University College， London：[s.n.]， 1974.

[14] 朱仁传， 缪国平. 船舶在波浪上的运动理论[M]. 上海：上海交通大学出版社， 2019.

[15] WU G X， EATOCK T R. A Green′s function form for ship motions at forward speed [J]. International Shipbuilding Progress， 1987， 34（398）：189-196.

[16] 邢瑞山， 卿光辉. 九节点 Hamilton 等参元列式[J]. 广东工业大学学报， 2012， 29（1）： 27-31.

[17] CHEN X， ZHU R C， MA C， et al. Computations of linear and nonlinear ship waves by higher-order boundary element method [J]. Ocean Engineering， 2016， 114： 142-153.

[18] MAURY C. Etude du problème de tenue à la mer avec vitesse d′avance quelconque par une méthode de singularité s de Kelvin [D]. cole France：cole Centrale de Nantes， 2000.

[19] YANG Y T， ZHU R C， Hong L. A frequency-domain hybrid HOBEM for motion responses and added resistance of ships sailing in head and oblique waves [J]. Ocean Engineering， 2019， 194： 106637.

[20] 杨云涛. 航行船舶运动的三维频域高阶面元法数值计算研究[D]. 上海：上海交通大学， 2020.

[21] 洪亮. 移动脉动源格林函数法及航行船舶在波浪中阻力增加的研究[D]. 上海：上海交通大学， 2017.

[22] TSUJIMOTO M， SHIBATA K， KURODA M， et al. A practical correction method for added resistance in waves [J]. Journal of the Japan Society of Naval Architects and Ocean Engineers， 2008， 8： 177-184.

[23] GUO B J， STEEN S. Evaluation of added resistance of KVLCC2 in short waves [J]. Journal of Hydrodynamics， 2011， 23（6）： 709-722.

[24] KASHIWAGI M. Hydrodynamic study on added resistance using unsteady wave analysis [J]. Journal of Ship Research， 2013， 57（4）： 220-240.

[25] FUJII H. Experimental study on the resistance increase of a ship in regular oblique waves [C]∥Proceedings of the 14th ITTC. Ottawa，Canda：[s.n.]，1975.

[26] NAKAMURA S， NAITO S. Propulsive performance of a container ship in waves [J]. Journal of the Society of Naval Architects of Japan， 1977，15：24-48.