半潜式起重拆解平台建造风险评估

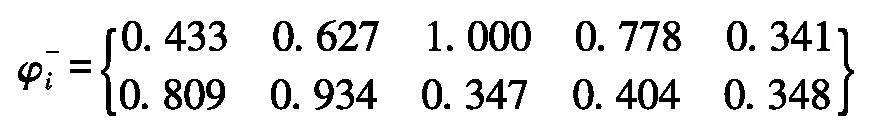
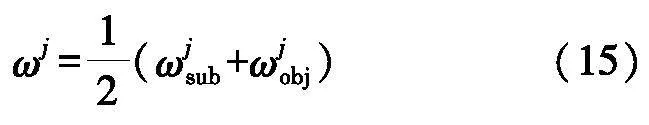
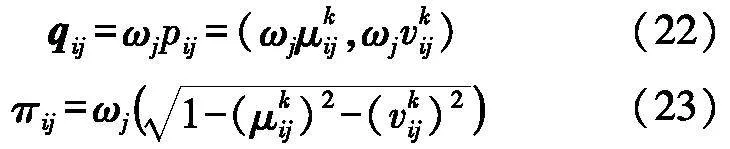
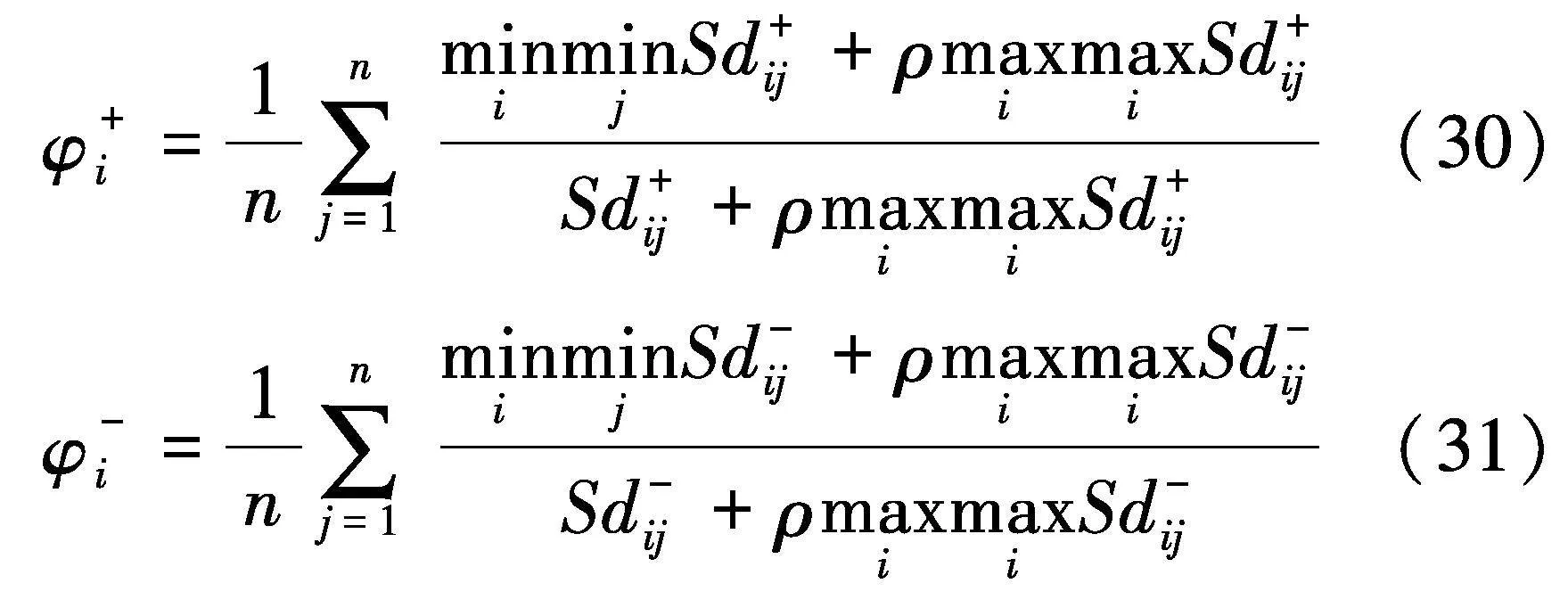
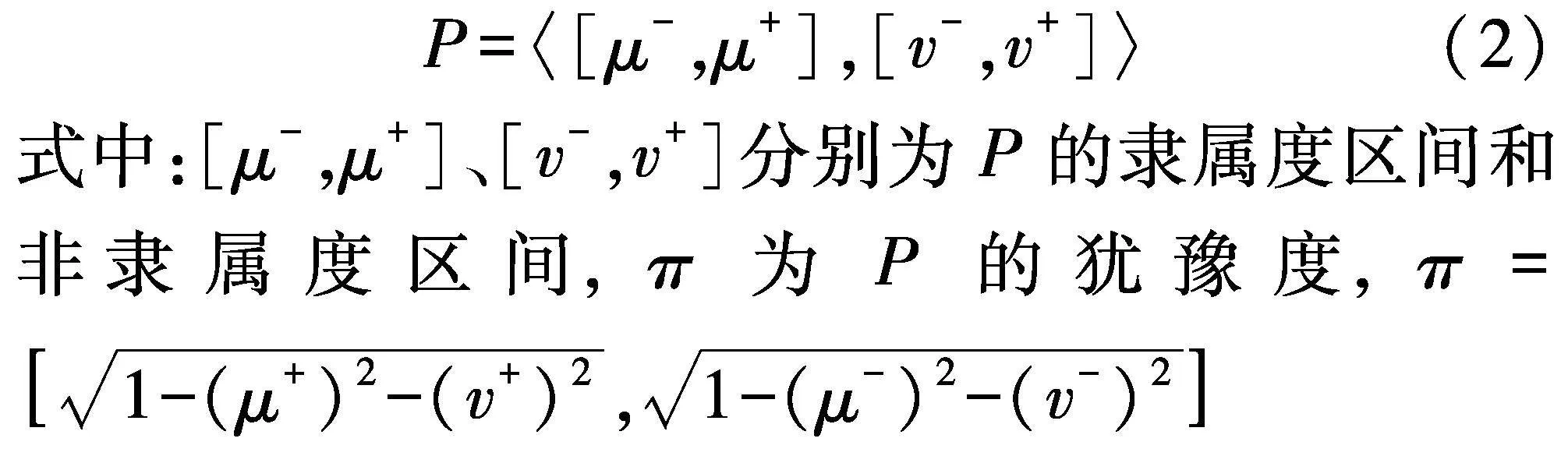
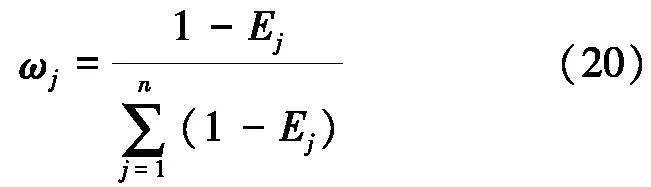
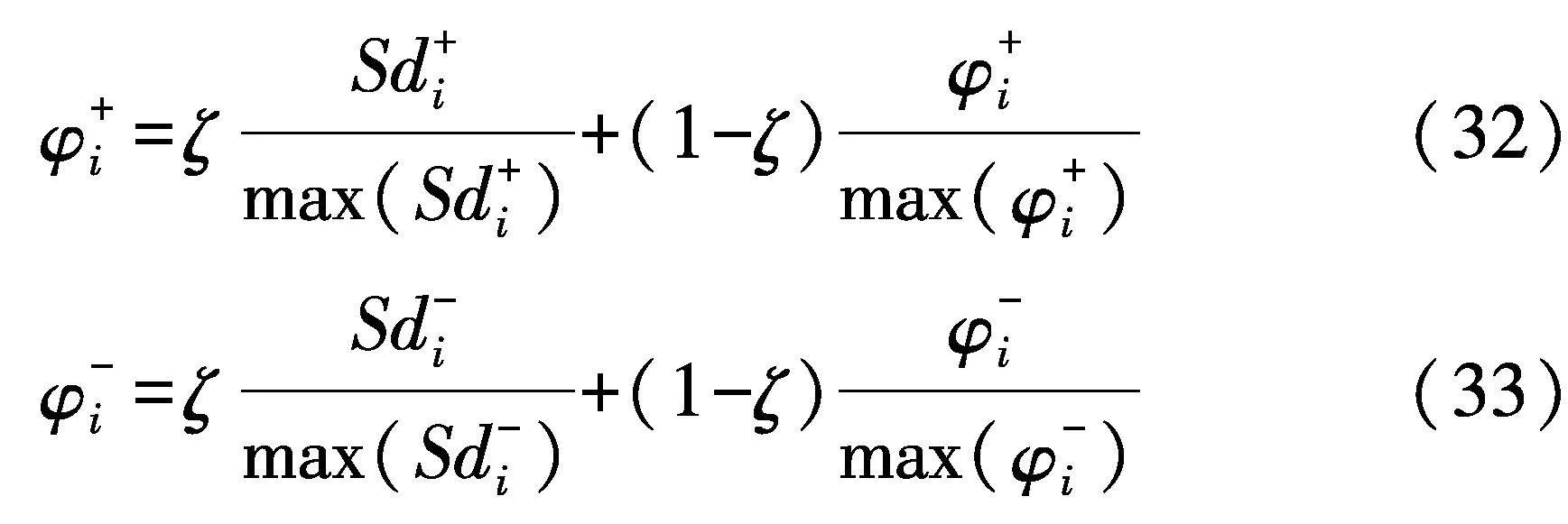
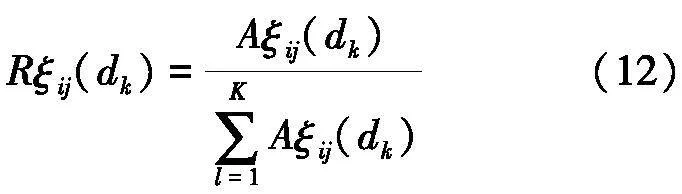
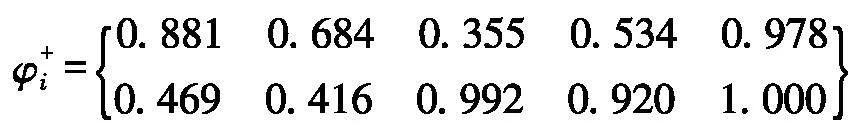
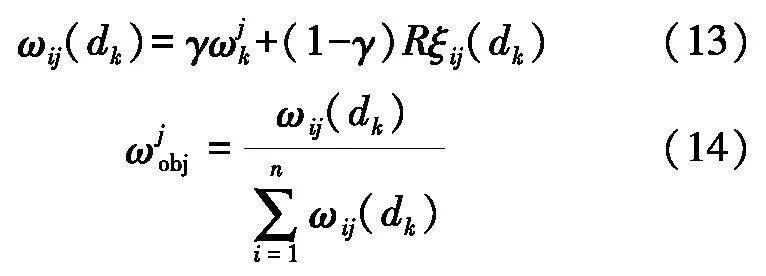
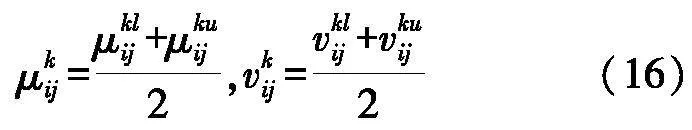
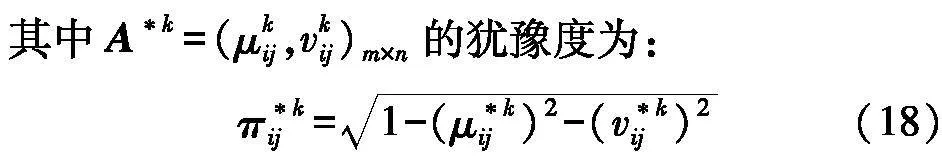
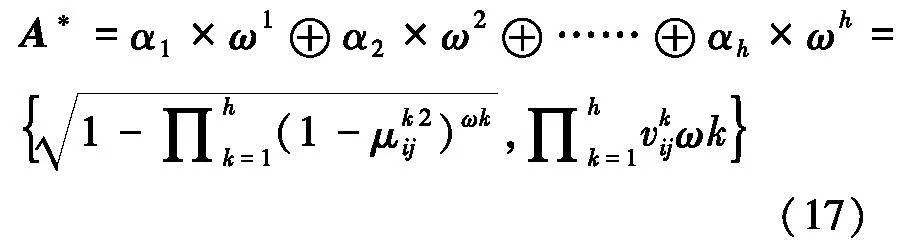
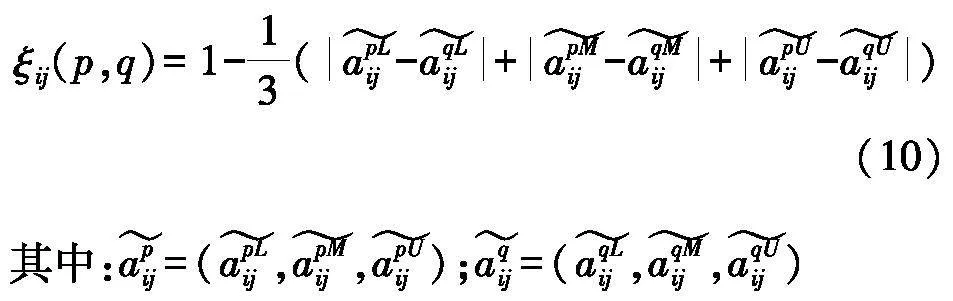
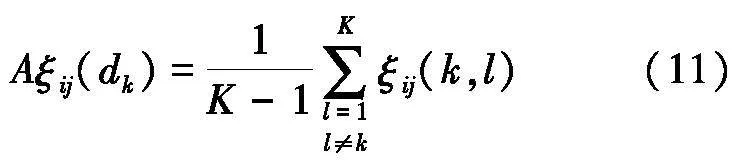
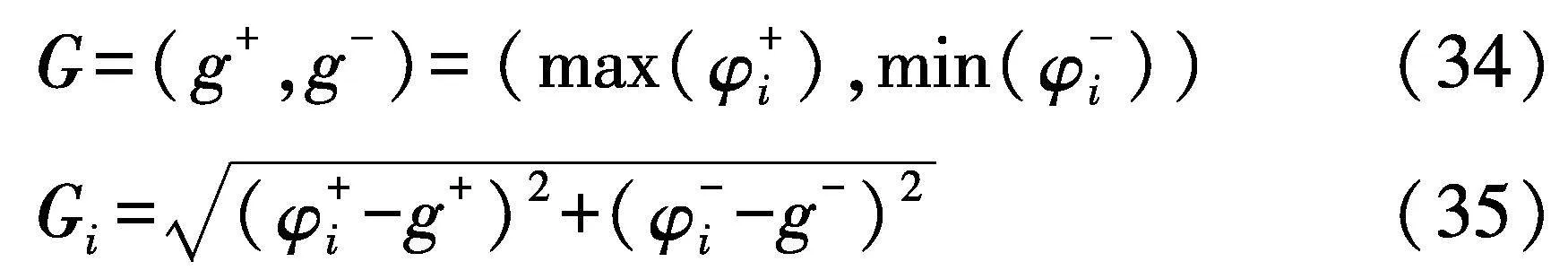
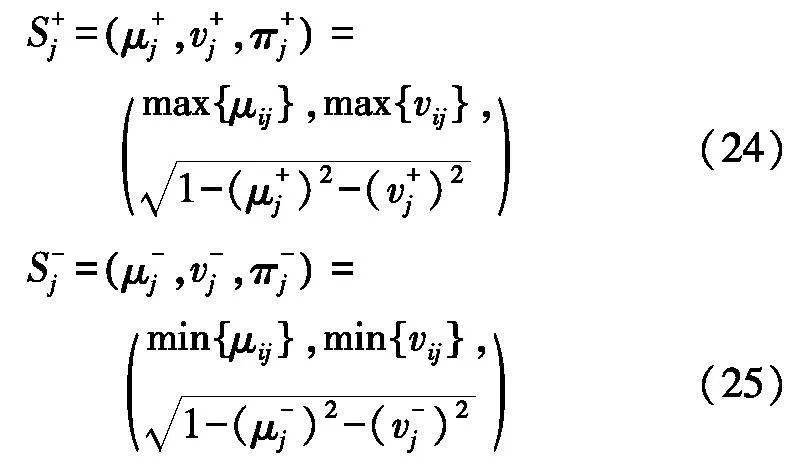
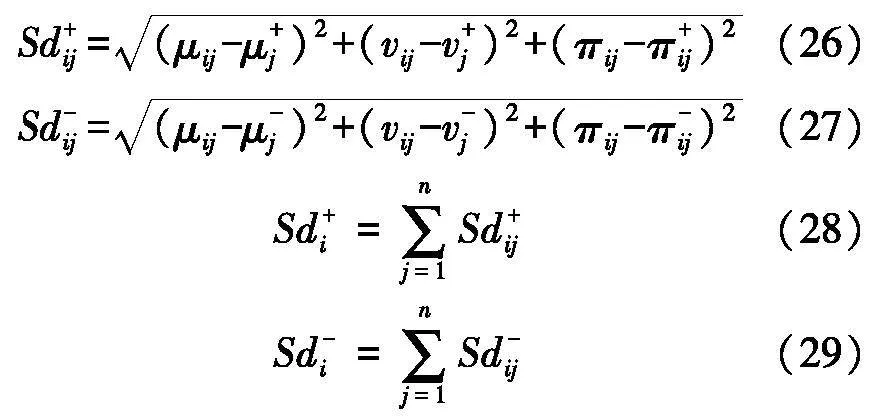
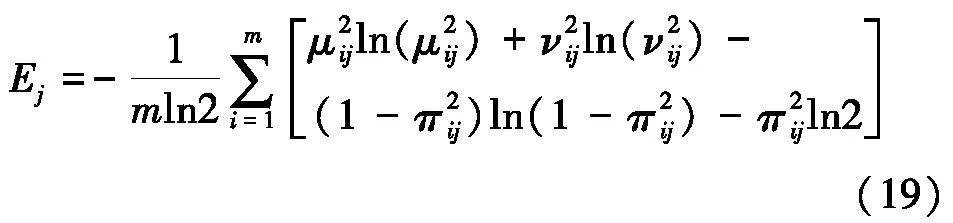
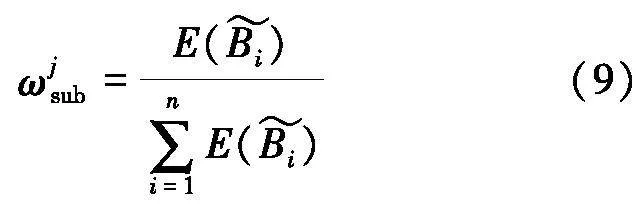
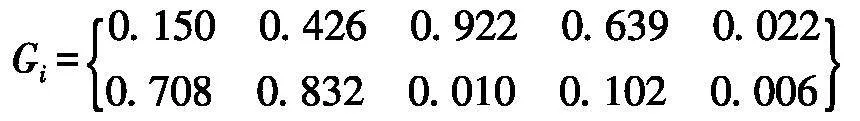
摘 要： 提出了一项包涵多数基本风险参数的整体风险评估模型，用于全面评估半潜式起重拆解平台的风险值.所应用的模型是三角模糊数、区间值毕达哥拉斯模糊（IVPFS）、优劣解距离法（TOPSIS）和灰色关联分析（GRA）的集成.将开发的IVPFS-TOPSIS-GRA应用到半潜式起重拆解平台建造风险评估的项目中：首先，应用三角模糊数获得了专家的重要性权重；其次，为避免决策者的主观性太强，提供了一种结合主观权重和基于相似度的客观权重的加权方法；再次，在区间值毕达哥拉斯模糊环境下结合TOPSIS-GRA获得已识别安全风险的最终排名.此外，进行了敏感性研究，验证所提出方法的鲁棒性和稳定性.通过对建造生产管理风险因素辨识的数据分析，得到建造生产管理风险的重点风险隐患区域：交叉作业生产管理区.结果表明，所提出的模型可以帮助专家在用模糊性和主观性语言处理的模糊环境中进行风险评估，克服了常见定量估计和定性估计的局限性.

关键词： 三角模糊数；主客观赋权法；IVPFS；TOPSIS-GRA；风险评估

中图分类号：U673.2;X820.4"" 文献标志码：A"""" 文章编号：1673-4807（2024）02-008-07

Construction risk assessment of a semi-submersiblelifting and dismantling platform

Abstract：We propose a holistic risk assessment model that encompasses most of the basic risk parameters for a comprehensive assessment of the risk value of a semi-submersible lifting and dismantling platform. The applied models are the integration of trigonometric fuzzy numbers， interval-valued Pythagorean fuzzy （IVPFS）， pros and cons solution distance methods （TOPSIS）， and grey correlation analysis （GRA）. The application of the developed IVPFS-TOPSIS-GRA to the project of risk assessment of the construction of semi-submersible lifting and dismantling platforms mainly involves the following work： First， the application of triangular fuzzy numbers has obtained the importance weight of experts; secondly， in order to avoid the subjective nature of decision makers， a weighting method that combines subjective weights and objective weights based on similarity is provided; third， in combination with TOPSIS-GRA in the interval-valued Pythagorean fuzzy environment， the final ranking of identified security risks is obtained. In addition， sensitivity studies are conducted to verify the robustness and stability of the proposed method. Through the data analysis of the identification of risk factors in construction production management， the key risk hidden areas of construction production management risks are obtained to be the cross-work production management area. The results show that the proposed model can help experts to conduct risk assessment in a fuzzy environment processed with ambiguous and subjective language， overcoming the limitations of common quantitative and qualitative estimation.

Key words：trigonometric fuzzy numbers， subjective and objective empowerment method， IVPFS， TOPSIS-GRA， risk assessment

自20世纪60年代以来，海上石油生产设施数量井喷式的增加，大量设施已面临或即将面临弃置拆解[1].基于旺盛的拆解市场需求及日益增长的拆解费用[2]，一种集“海上吊车”和“海上住宅”于一体，耐波性良好，海况适应能力强，有着独到的拆解作业优势的非对称无横撑半潜式起重拆解平台应运而生.然而其特殊的结构、布置和设备属性，给生产建造带来了不小的挑战，为保证平台安全、高质、高效完成，需着重其特殊性进行建造风险评估，以提高平台建造过程中的抗风险能力.涉及到评价问题，如何处理带有一定主观性的专业性意见尤为重要，文献[3]将主客观赋权法运用到通讯设备的抗干扰能力评价中，既有效利用了实际观测数据，还在一定程度上避免了决策者的主观性过强.文献[4]通过PHAST软件模拟内河LNG运输船LNG泄漏事故后果，定量的评估了火灾爆炸事故的影响范围.现阶段评估方法不再局限于定性评估、定量评估.大多数常用评估方法都是基于对原始数据的利用，无法捕捉到原始数据中涉及的不确定性和模糊性.为了应对这种情况，文献[5]建立了模糊集（FS）的概念.由于其独特的优势，模糊集在不同的研究领域有很多应用[6-7].在模糊集理论中，一个对象的非隶属度被描述为它的隶属度到1的补码.文献[8]探索了直觉模糊集 （IFS）的概念，作为模糊集的扩展，直觉模糊集由隶属度和非隶属度描述，其总和限制为1，因此可以更全面地表示数据的不确定性.受 IFS 的启发，文献[9]通过推广隶属度和非隶属度的范围，提出了毕达哥拉斯模糊集（PFS）的概念，其中隶属度和非隶属度的平方和≤1，约束条件的限定使得PFS 在处理实际应用中的模糊性方面更加出色.在此基础上，文献[10]提出了区间值毕达哥拉斯模糊集 （IVPFS）的概念.与精确数值相比，模糊集的利用使得评估数据更具可解释性，可以进行更切实的评估.

1 区间数和模糊集相关理论

1.1 三角模糊数

三角模糊数A=（aL，aM，aU），aL和aU分别为A所支撑的上下界，aM为A最可能的值，其隶属函数为：

1.2 区间值毕达哥拉斯模糊集

设U为论域，其U上的一个区间值毕达哥拉斯模糊集P定义：

1.3 优劣解距离法

优劣解距离法（pros and cons solution distance methods，TOPSIS）[11]常用于综合决策问题，基于各方案与正负理想解的相近程度进行排序，相近程度越高越接近理想方案，反之越接近最劣方案，由于其计算简单、数据量小，得到了广泛的应用.

1.4 灰色关联分析法

灰色关联分析法（grey correlation analysis，GRA）根据若干数据列之间发展趋势的相似或相异程度，即“灰色关联度”，判断其关联紧密程度，是一种适用于小样本数据的多因素统计分析方法.

2 算法描述

2.1 算法框架

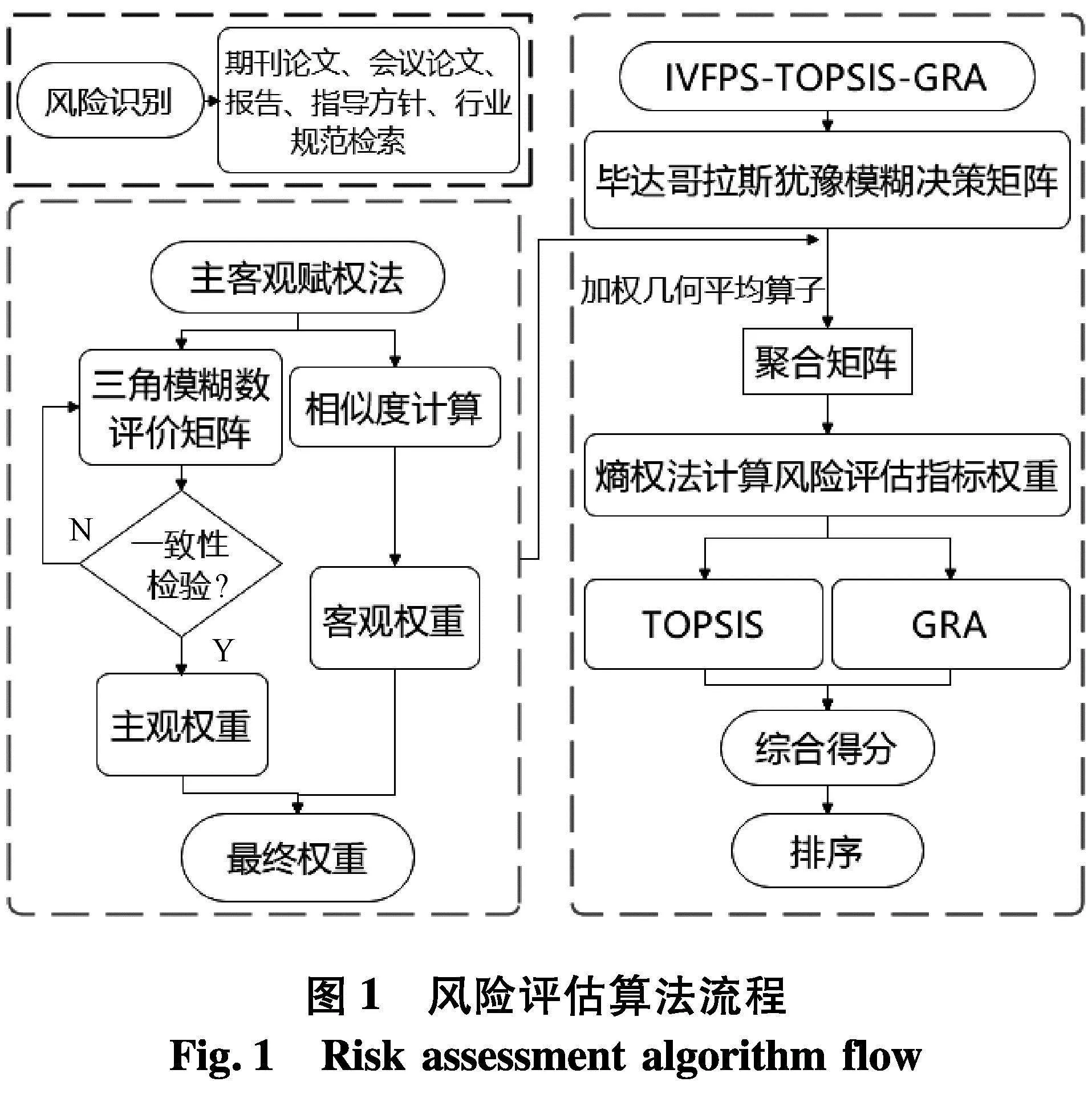
文中提出的应用的算法框架如图1.

2.2 风险评估框架的建立

风险评估全过程最首要的就是风险识别，风险识别的正确与否影响着评估结果的准确性，遗漏、错误识别风险都会导致评估结果失效.对于某一目标所涉及到的风险，应尽可能全面精确的概括总结.风险识别需要应用恰当的评估方法，评估方法应尽量简便、评估效果精确且评价来源可靠，下面为本问风险评估框架的建立过程.

2.2.1 主客观权重赋值法获得专家权重

（1） 确定主观权重

通过三角模糊数的应用，决策者就若干指标进行评价得到指标的相互重要权重，就各指标对专家进行评估作为专家得分，通过相互重要权重与专家得分的运算得到主观权重.

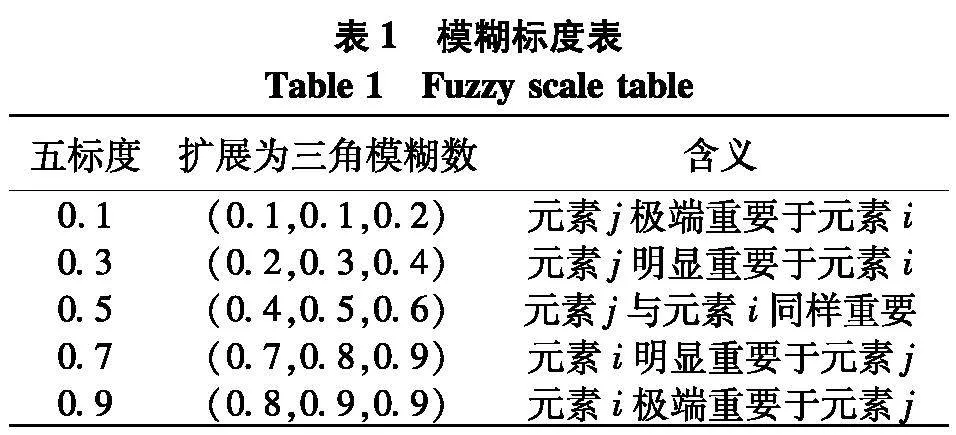
决策者利用表1就各指标进行两两比较后给出评价结果，形成互补判断矩阵.

互补判断矩阵中元素aij=（aLij，aMij，aUij）.

一致性指标CI为：

一致性比例CR为：

如果CRlt;0.1，表明判断矩阵有效，不满足则修改互补判断矩阵.

计算三角模糊数权重，记w=（w1，w2，…，wn）， wi=（wLi，wMi，wUi）.

通过式（9）计算最终主观权重为：

（2） 确定客观权重

通过计算决策者与决策总体评价值的相似度，得到决策者dj对于专家ek的客观权重.

计算两个决策者对于专家在若干指标下的相似度ξkj（p，q）为：

其中：apij=（apLij，apMij，apUij）；aqij=（aqLij，aqMij，aqUij）

根据式（11），计算决策者dj对于专家ek在指标下的评价值和群体决策者评价值的平均相似度Aξij（dk）为：

根据式（12）计算相对相似度为：

通过式（13-14）计算最终客观权重：

（3） 计算最终权重

取主观权重和客观权重的平均值作为最终权重为：

2.2.2 IVPFS-TOPSIS-GRA评估方法

（1） IVPFS

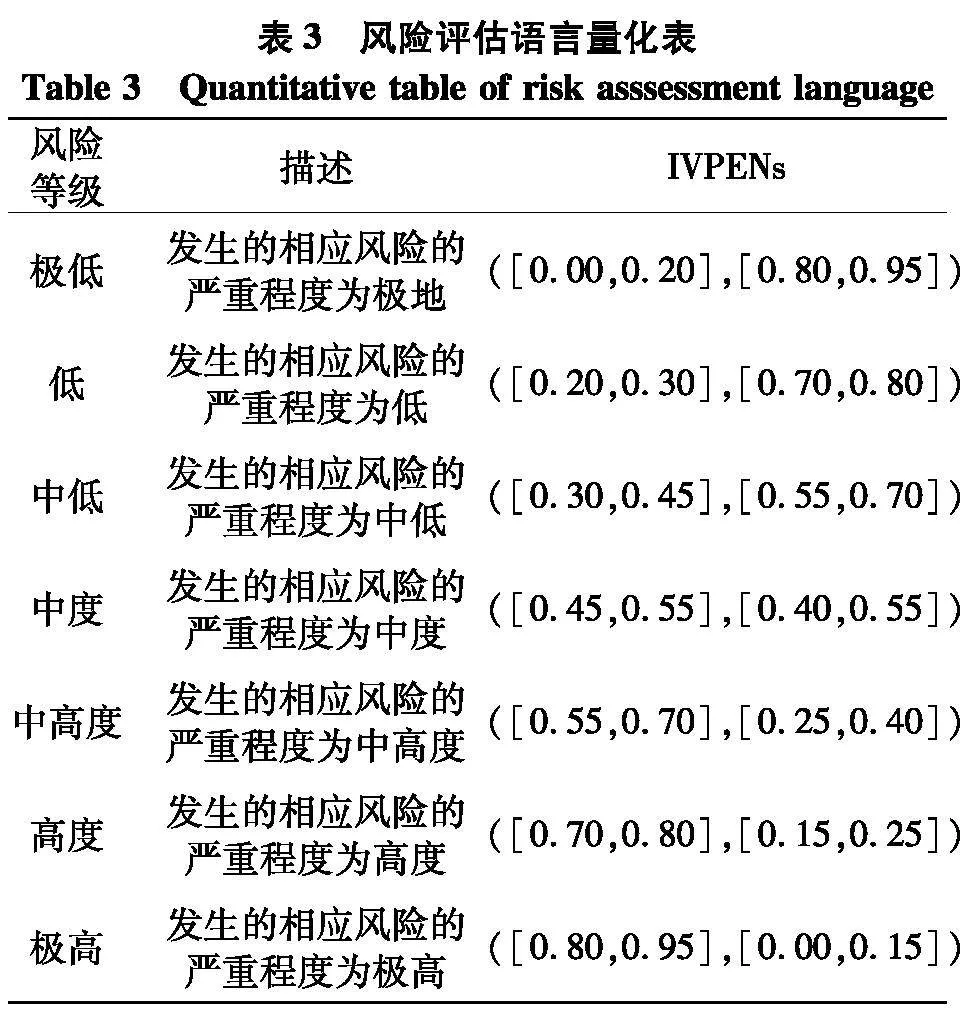
建立区间值毕达哥拉斯模糊决策矩阵，并对数据进行规范化处理.表3为风险评估语言量化表，针对不同的风险指标其语言变量的表述不尽相同，最右列为语言变量所对应的区间值毕达哥拉斯模糊集.

专家根据量化表对风险因素进行评估，Ak=（μklij，μkuij，vklij，vkuij）m×n，k=1，2，…，h

通过式（16）得到毕达哥拉斯模糊决策矩阵A，其中Ak=（μkij，vkij）

通过式（17）对专家的风险评估矩阵进行聚合，使用加权几何平均算子得到聚合风险矩阵A为：

式中，ω1，……，ωh是与所涉及的专家的聚合权重.

（2） 熵权法获得风险指标权重

信息学家认为信息源是唯一确定的，信息熵代表着信息传递的不确定性的大小，离散度越大，蕴含的信息越不可靠，权重越小.因此可利用信息熵这个工具，计算出各个指标的权重，为多指标综合评价提供依据.根据聚合风险矩阵中各风险评估指标的性质将指标正向化.

对于处理过的聚合风险矩阵R=（rij）m×n，其信息熵Ej为：

风险评估指标权重ωj为：

式中，1-Ej为信息熵冗杂度.

（3） TOPSIS-GRA综合排序

归一化聚合评价矩阵pij为：

pij=（μkij，vkij） 效益型

熵权决策矩阵qij为：

正负理想解S+j与S－j为：

各方案与正负理想解的距离Sd+i与Sd－i为：

计算熵权灰色关联度φ+i与φ－i为：

2.2.3 计算综合距离

各方案的正负综合距离φ+i和φ－i为：

2.2.4 计算各风险到理想参考点G的距离

通过式（34）得到综合距离中的理想参考点G，再由式（35）得到各方案到理想参考点的距离Gi：

2.2.5 风险排序

对各方案进行排序，最终得分Gi越低，得分越低，相对风险就越大.

3 实例应用

3.1 平台特点

半潜式起重拆解平台相较常规运输船有较大区别，该平台示意图如图2[12].

平台由不对称的两侧浮箱、左右各两立柱和一个上船体组成，立柱之间无横撑，驾驶室外悬于小浮箱一侧，大浮箱一侧工作甲板上配有双2 200 t单吊.上船体有4层甲板，除主甲板外，其余甲板分别布置有居住室及各类舱室，立柱内布置有快速压载舱，动力系统位于起重船艉部，6个推进器四二分布于大小浮箱内.其建造过程中，存在着大量的风险隐患，针对其特殊的布置结构与设备属性总结建造难点如表4.

密切关注过去在生产建造管理方面的研究，包括期刊论文、会议论文、报告、指导方针等，获得主要来源于三大类10个风险因素如表5.

第一类：生活区生活安全风险

第二类：生活区生活质量风险

第三类：生活区与作业区交叉管理风险.

3.2 主客观权重赋值法

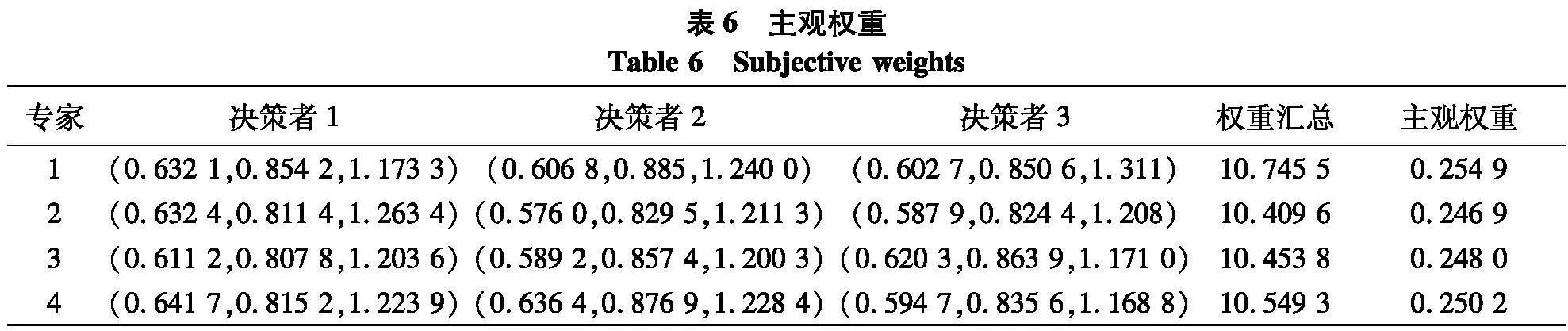
由3位决策者来衡量4位专家的重要性权重.为衡量专家的重要性权重，选取4项考察指标：经验e（即在船厂工作的年数）、学位d（专家在船舶行业或管理相关领域获得的最高学历）、专业资格p（专家获得的职业技能证书），以及研究概况r（有关船舶行业安全管理领域相关的科研成果），3位决策者就四项考察指标，分别建立三角模糊数互补判断矩阵，计算考察指标的相互依赖权重，并对4位专家进行打分，将相互依赖权重与各专家得分的乘积作为最终得分，进行归一化处理后得到专家的重要性主观权重.计算得到专家的主观权重如表6.

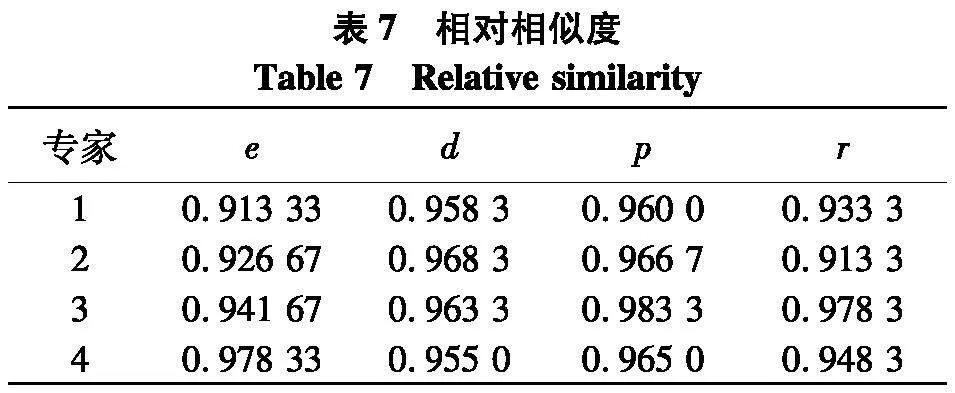
计算决策者对于专家在各项考察指标评价值的相对相似度Rξij（dk）.如表7.

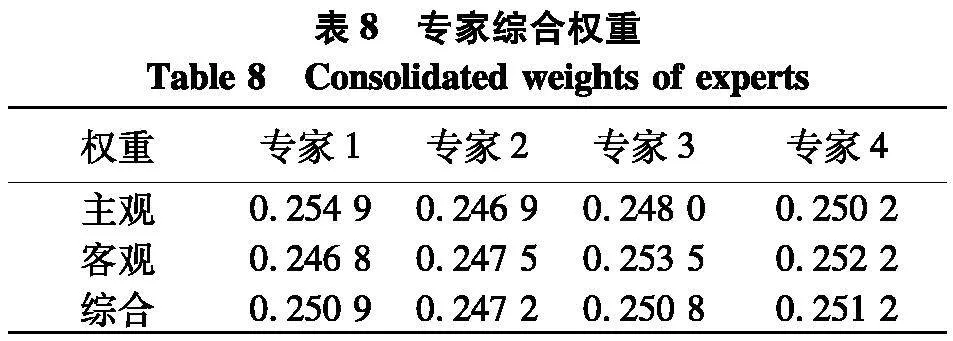
综合考虑决策者个体与群体的意见，根据式（13-14），利用相对相似度计算专家就4项评价指标的客观权重，后采用主客观权重赋值法得到专家综合权重，如表8.

3.3 形成聚合决策矩阵

为评估半潜式起重平台的建造风险，采用Saeed Reza Mohandes[12-13]对风险的描述，包括：严重性S、概率P、暴露程度E、可检测性D、对保护措施失效的敏感性SFB、对恶劣气候的敏感性SPSC、对不良现场安全条件的敏感性SPSSC和对恶劣环境条件的敏感性SBEC.4位专家参照风险语言量化表对各类风险就8项风险指标进行评估，得到各自的评价矩阵.

利用加权几何平均算子对专家的评价矩阵进行聚合生成聚合风险决策矩阵.

3.4 熵权法获得评价指标权重

各项指标均为效益型指标，即聚合风险矩阵指标已正向化，通过式（19-20）分别计算聚合风险决策矩阵中各风险评价指标的信息熵Ej与权重wj，如表9.

3.5 生产管理风险综合评估

利用TOPSIS方法，获得聚合风险决策矩阵中的正负理想解S+与S－.

计算各风险到正负理想解的加权距离Sd+i与Sd－i和灰色关联等级φ+i和φ－i，通过线性求和得到综合正负距离.

计算各风险的综合正负距离到理想参考点G的排序距离.

对各风险进行排序，排序结果：RS10lt;RS8lt;RS5lt;RS9lt;RS1lt;RS2lt;RS4lt;RS6lt;RS7lt;RS3.RS10得分最低，RS8次之，得分越低则风险值越大，可见生活区人数与重叠区域面积这两个因素是生产管理方面需要着重注意的地方.

4 敏感性分析

对TOPSIS-GRA方法进行敏感性分析[13]，对参数ζ在[0，1]范围内进行了以0.1为步长的参数调整（见表10）.当ζ为0时，退化为单GRA排序，当ζ为1时，则为单TOPSIS排序.

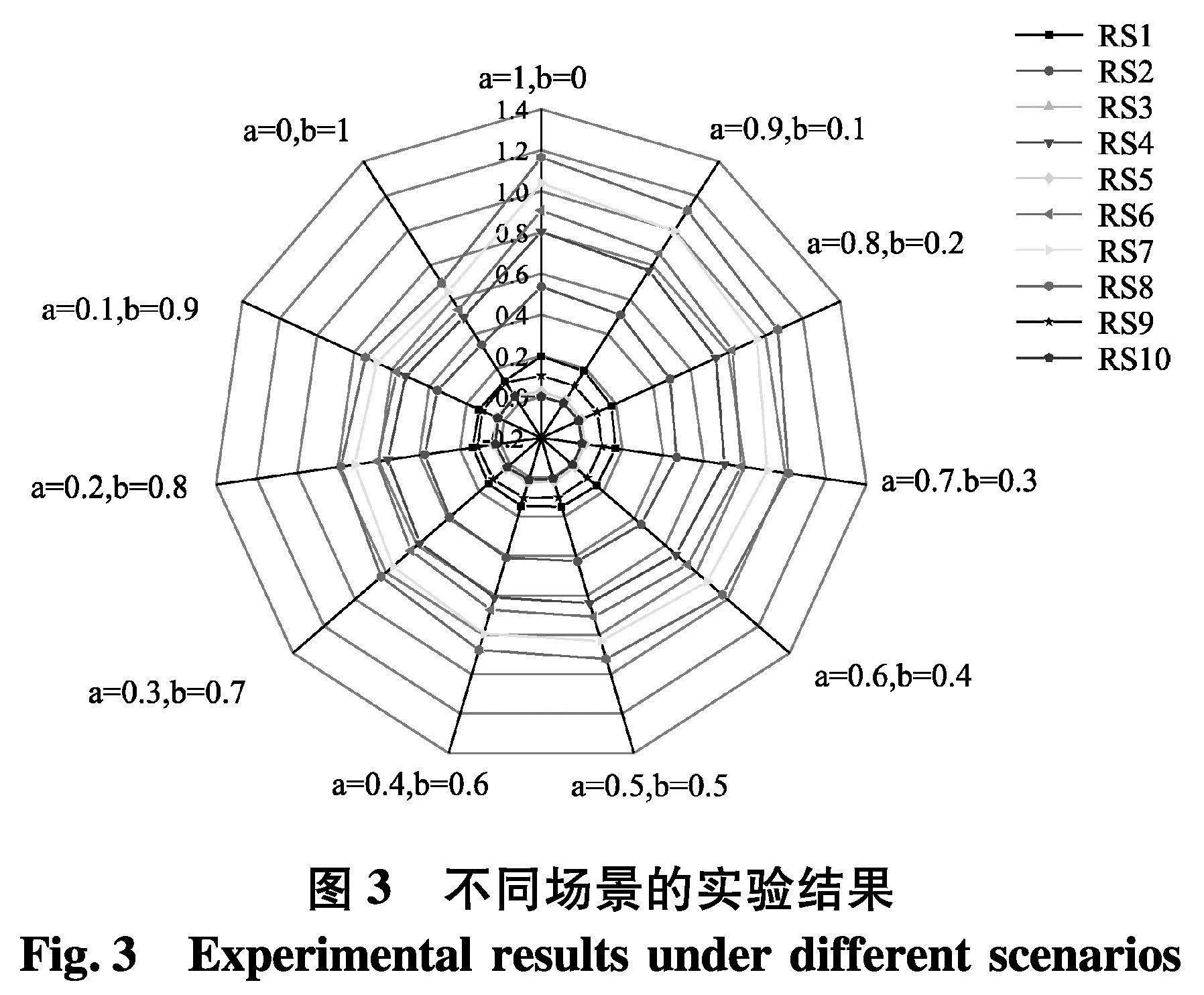
将各场景得到的排序结果绘制成图3.

实验结果表明涉及到专家的意见，排序结果具有良好的一致性.

5 结论

基于建造生产管理风险因素，构建建造生产管理风险模型，通过对建造生产管理风险因素辨识的数据分析，得到建造生产管理风险因素的危险排性序：

（1） 生活区生产人数、重叠区域面积与重叠工种数量这三个因素得分很低，生产区域过小或人数过多不利于生产作业的展开；交叉作业更是事故发酵的温床.

（2） 基本生活保障因素得分较低，生活保障不完备会影响工作的正常开展，良好的基本生活保障是安全生产的保护伞.

（3） 建造生产管理风险的重点风险隐患区域为交叉作业生产管理区.

参考文献（References）

［1］ 王勇，戴兵，高军伟. 废弃海洋石油平台的拆除[J].机械工程师，2010（1）：134-136.

[2] 田华勇， 李福建，杨玥.半潜式起重拆解平台对海上拆除作业的适应性[J].中国海洋平台， 2020，37（1）：30-35.

[3] 宋冬梅，刘春晓，沈晨，等. 基于主客观赋权法的多目标多属性决策方法[J]. 山东大学学报（工学版），2015，45（4）：1-9.

[4] 王庆丰，崔相义.内河水域LNG运输船泄漏事故的定量风险评估[J].江苏科技大学学报（自然科学版），2019，33（1）：16-20.

[5] ZADEH L A，" Fuzzy sets Inf ormation amp; Control，1965，8（3）：338-353.

[6] BOSE A， MALI K， Type-reduced vague possibilistic fuzzy clustering for medical images[J]. Pattern Recognit，2021，112：107784.

[7] SUN S. Application of fuzzy image restoration in criminal investigation[J].Journal of Visual Communication and Image Represent，2020，71：102704.

[8] ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems，1986，20：87-96.

[9] YAGER R R." Pythagorean membership grades in multi-criteria decision making[J]. IEEE Trans" Fuzzy Syst， 2014（22）：958-965.

[10] PENG X， YANG Y. Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators[J]. International Journal of Intelligent Systems，" 2015，31： 444-487.

[11] 刘天寿，匡海波，刘家国，等.区间数熵权TOPSIS的港口安全管理成熟度评价[J].哈尔滨工程大学学报：2019，40（5）：1024-1030.

[12] 刘建成，凌晨，谷家扬，等.半潜式起重平台拆解作业安全监测系统[J].船舶工程，2020，42（8）：122-128.

[13] MOHANDES S R， ZHANG Xueqing. Developing a holistic occupational health and safety risk assessment model： An application to a case of sustainable construction project[J]. Journal of Cleaner Production，2021， 291：125934.