真探深究，让学习走向深度

【摘 要】交换律教学的核心价值在于对其本质的理解，文章通过举例子、数数、线段图等多元表征方式，加深学生对加法交换律本质的理解，并在此过程中重视研究方法的拓展和迁移运用，从而研究对乘法、除法、减法相关问题的，实现从一个问题的研究上升到一类问题的研究，培养学生的迁移运用能力以及模型思想。

【关键词】交换律 多元表征 应用拓展

对于“加法、乘法交换律”这两个运算律，学生在以前的计算和解决实际问题的过程中，就已经积累了一定的经验。但是对于加法、乘法交换律的本质和内涵还是比较模糊，多数学生的思维只停留在结果相等上，而未能体会到过程的不同。史宁中教授指出，在数学教育中，无论从时间上还是内容上都应当对归纳推理给予足够的重视，应当让学生在学习过程中，逐渐感悟这种推理模式的“自然”属性。而加法交换律和乘法交换律无论是在形式上还是在证明方式上都存在很多相似之处。因此，可以先让学生经历加法交换律的推理过程，在此基础上进行猜想并合情推理，从而总结出乘法、除法、减法是否有此运算律。基于以上思考，对“加法、乘法交换律”这一课做了如下教学尝试。

一、学习目标

1.经历观察、猜想、验证、归纳加法交换律的探究过程，并能类比推理得出乘法交换律以及用文字或字母等表示加法、乘法交换律。

2.通过举例、数数、图式等方式解释所发现规律，了解其丰富的现实背景。

3.培养发现问题和提出问题以及合情推理能力，积累数学活动经验，发展应用意识。

二、教学过程

一、巧设情境，激发兴趣

师：同学们，听说我们班同学的口算能力特别强。请你们快速说出下面算式的答案。（依次出示下面三道算式）

6+5= 97+46= 123+4=

生：11，143，127。

师：下面算式的答案呢？（依次出示：5+6= 46+97=）

生：11，143。（此时学生已跃跃欲试想说出第三题的题目和答案）

师：猜一猜，下一题的算式会是什么样子？

生：前面两道题都是把两个数倒过来的，所以下一题应该是4+123。

师：是不是像你们猜想和推理的那样？我们一起来揭开谜底。（出示算式：4+123）观察这些算式，除了两个数交换了位置，还有什么发现？

生：我还发现交换位置后，它们的和是不变的。

师：既然和不变，我们就可以用等号把它们连接起来。（板书：6+5=5+6，97+46=46+97，123+4=4+123）

（设计意图：通过口算，学生快速得出答案，一方面有利于激发学生的学习兴趣，另一方面也便于学生观察和发现规律。特别是最后一题，教师特意放慢节奏，让学生通过观察已有算式的特点，发现其规律并为初步猜想做好铺垫。）

（二）尝试猜想，多元验证

1.举例验证

师：刚才我们通过计算，发现这三个算式，交换加数的位置，它们的和不变。仅仅从这三个算式，就得出一个结论，可能不太严谨。我们暂且看成是一种猜想。既然是猜想，就要怎么样？

生：验证。

师：你们想怎么验证？

生：可以再举一些例子试试，看看是不是也有这样的规律。

师：再举一些例子来证明，确实是一种不错的方法。我们就在学习单上也试着举一些例子，看看是否也有这样的规律。

（学生独立思考、汇报交流）

生：14+5=19，5+14=19，14+5=5+14；42+44=86，44+42=86，42+44=44+42；4+8=12，8+4=12，4+8=8+4。

师：这些例子，能否验证我们的猜想。（能）你们举的例子都能验证吗？（都满足）有没有哪个同学交换两个加数的位置后，它们的和发生变化的？（没有）

师：看来通过举例的方式可以证明我们的猜想是正确的。

（设计意图：结合学生已有经验，通过照样子举例子的方式，让学生初步体会不完全归纳法。同时在思考过程中，引导学生用“因为……所以”等规范的数学化语言来验证猜想。最后通过追问“有没有交换后，它们的和发生变化的”这一问题渗透举反例的数学思想。）

2.生活实例验证

师：其实一年级，就学过用另一种方式证明这个猜想是正确的。如树上有3只小鸟，地上有5只小鸟，一共有多少只小鸟？我们可以怎样列式？

生：3+5。

师：也可以怎样列式？

生：5+3。因为3+5=5+3。

师：看来我们通过生活实例也可以证明这个猜想。

（设计意图：通过简单的生活实例，以回顾旧知的形式，再一次证明猜想的正确性。）

3.数数验证

师：除了这两种方式外，我们在一、二年级还学了另外一种方法来证明这个猜想，请观看视频（播放青蛙跳的视频，第一只青蛙从4开始一格一格跳了7格。第二只青蛙从7开始一格一格跳了4格）。

师：观察刚才的视频，你有什么发现？

生1：一个是4在前面，一个是7在前面，最终跳到的位置还是一样的。

生2：第一只青蛙开始的4格就是第二只青蛙后面的4格。第一只青蛙后面的7格就是第二只青蛙开始的7格，只是交换了位置。

生3：第一只青蛙先跳了4格，再跳了7格。第二只青蛙先跳了7格，再跳了4格。最后，它们都落在同一个位置。

师：第一只青蛙先跳4格和第二只青蛙先跳7格后，是怎么跳到最终位置的。

生4：一格一格跳的。

师：怎样用数学语言表达？

生4：+1，+1。

生4：我还发现，虽然两只青蛙跳的过程不一样；但结果都是一样的。

师：第一只青蛙跳的过程，我们可以怎样用算式表示？

生5：4+7。

师：第二只青蛙跳的过程，我们可以怎样用算式表示？

生6：7+4。

师：既然它们跳到了一样的位置，我们就可以怎样用算式表示？

生：4+7=7+4。

师：看来通过数数的方法，也可以验证我们的猜想是成立的。

（设计意图：根据自然数公理法则，加法的实质是在原来的基础上，一个一个往后数的结果。为了让学生感受这一数学本质，体会数数过程，题目特意隐去最终结果11。通过引导，让学生经历4+7就是在4的基础上，一个一个往后数7个1，7+4就是在7的基础上，一个一个往后数4个1的过程。体会和感受4+7和7+4这两个算式的过程不同，结果一样。）

4.图式验证

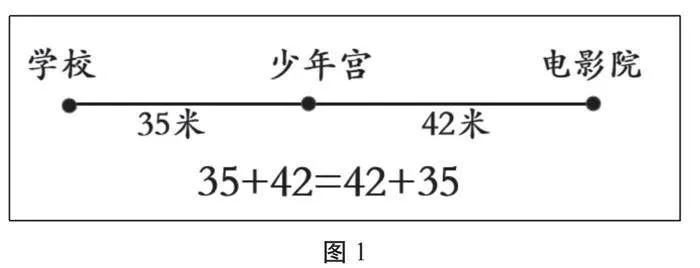
师：你会结合图1，说说我们的猜想是成立的吗？

图1

生：从学校到电影院的距离等于电影院到学校的距离，所以可以列式35+42=42+35。

师：如果距离分别是50、60，结合这幅图，你会写出哪个等式？

生：50+60=60+50。

师：如果距离分别是140、168，你又会写出哪个等式？

生：140+168=168+140。

（设计意图：通过数形结合的图式，直观明了，让学生理解猜想的成立。同时通过不断变换数字的方式，为过渡到用字母表示猜想做好铺垫。）

师：如果用a和b表示呢？

生：a+b=b+a。

师：这里a是什么意思？b又是什么意思？

生：a表示学校到少年宫的距离，b表示少年宫到电影院的距离。

师：这里的a和b可以表示什么数字？

生：100、200MYCpwR5JYD1MjbNMzBHxXQ==、500、600。

师：小数行不行？

生：也行。

师：说得完吗？

生：说不完。

师：看来用图式的方式，也可以证明我们的猜想是成立的。

（设计意图：结合图式，通过从具体数字变化到字母表示，以及适时的追问，让学生进一步感受到加法交换律具有一般性的特征，加深对加法交换律本质的理解。）

（三）归纳总结，得出结论

师：通过四种方法证明了我们的猜想是正确的。a+b=b+a就是我们所说的加法交换律。今天我们就来学习加法交换律。（板书课题）

师：回顾一下，我们是怎么得到这个加法交换律的？

（设计意图：通过引导学生回顾加法交换律得出的全过程——计算、观察、猜想、验证、结论，培养学生积累解决相关问题的活动经验。）

（四）合情推理、拓展应用

师：加法中，有加法交换律，你还有什么猜想？请把你的猜想写在学习单上并验证。（学生独立操作，交流汇报）

生1：我发现乘法有交换律。如1×2=2，2×1=2，1×2=2×1。

师：举一个例子就说明有，会不会太草率了？

生2：我举得多一些，如3×5=15，5×3=15，3×5=5×3；11×2=22，2×11=22，11×2=2×11；10×20=200，20×10=200，10×20=20×10。通过这些算式也可以发现乘法有交换律。

师：你们从举的例子中也可以发现乘法有交换律吗？

生：有。

师：如果把两个数字换成a和b，等式就可以写成什么？

生：a×b=b×a。

师：这就是数学上所说的乘法交换律。（板书）

生1：我发现36÷9≠9÷36，所以我认为除法没有交换律。

生2：我却发现36÷36=36÷36，8÷8=8÷8，这种被除数和除数相等时，都满足交换律的条件。

师：有些除法算式满足交换律的条件，有些不满足，除法有没有交换律呢？

生3：只是在特殊情况下才有，特殊性不代表一般性。如正方形是特殊的长方形，正方形四条边相等，但我们不能说长方形的四条边都相等。所以除法是没有交换律的。

师：以此类推，减法有没有交换律呢？

生：没有。

师：看来只有加法和乘法有交换律，除法和减法是没有交换律的。

（设计意图：通过证明加法交换律的活动，合情推理出乘法、除法以及减法是否有此规律，并在过程中体会和感受一般性和特殊性，进一步培养学生的推理和解决问题能力。）

三、教学思考

（一）巧设情境，让规律有章可循

四年级的学生对于算式是否相等，主要通过算式的结果是否相等这一条件进行判断。因此本课伊始，学生直接从三组加法算式入手，通过对算式的计算和观察，发现其中的规律并形成初步的猜想，同时对猜想进行验证和解释，最终得出结论。这一系列的研究过程为后面学生自主探究其他规律奠定了基础。

（二）多元表征，让学生理解本质

在对加法交换律这一规律解释上，除了模仿举出一些算式以及生活实例外，还利用数形结合的图式方法，让学生直观明了地体会到加法交换律的合理性。同时，还通过青蛙跳的情境，让学生理解加法的实质就是在原来的基础上，往后一个一个数的过程，这个过程中虽结果一样，但过程是不同的，学生真正对加法交换律的本质和内涵以及来龙去脉有了更清晰的认识和理解。

（三）合情推理，让学习走向深度

史宁中教授指出，在数学教育中，无论从时间上还是从内容上都应当对归纳推理给予足够的重视，应当让学生在学习过程中，逐渐感悟这种推理模式的“自然”属性。加法交换律和乘法交换律无论在形式上还是在探索方法上都存在相通、相似的地方，因此，本节课的学习是让学生经历发现加法交换律的归纳推理全过程，并通过合情推理、猜想、验证乘法、除法、减法是否有此规律。特别是在推理除法、减法是否有此规律时，通过交流汇报以及举例方式，让学生理解特殊性并不能代表一般性的逻辑思想，从而使学习真正走向深度。

【参考文献】

[1]中华人民共和国教育部义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022

[2] 刘祖希. 访史宁中教授：谈数学基本思想、数学核心素养等问题[J].数学通报.2017（5）.