数学建模思想引领的一次函数的应用教学设计

【摘要】数学建模是数学学科核心素养之一.数学建模主要表现为：发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题.本节教学设计通过图象的形式呈现了生活中的几个问题情境，要求学生通过观察、分析获取有用的信息，建立一次函数模型，使学生在活动中学会解决实际问题的方法，体会“数学建模思想”的重要性.

【关键词】数学建模；一次函数；教学设计

1课题：一次函数的应用第一课时

课型：新授课

课时：第一课时

2教材分析

本节课是鲁教版七年级上第六章的一次函数第五节的第一课时，其主要内容是在学生已经学习了一次函数的意义、一次函数的图象及其性质、确定一次函数的表达式的基础之上进行的.

通过这一节课的学习使学生掌握一次函数图象和性质，并能简单应用性质.理解一次函数解析式中k和b的实际意义，学会从实际问题所给的图象中识别分析出关键有用的信息，理解图象中自变量和因变量的意义，建立一次函数模型解决实际问题.让学生体会到数学学习过程中“数形结合”“方程与函数”“数学建模”思想的重要性.

3学情分析

在前面的学习过程中，学生已掌握了函数特别是一次函数的概念，认识了一次函数的图象是一条直线，学会了如何作图，并学习了图象的性质.学会用图象法、列表法、解析式法这三种方法去表示函数.在此基础上，由于学生直接利用函数图象解决问题的意识仍比较薄弱，为此设计了本节内容.具体为：通过图象的形式呈现了生活中的几个问题情境，要求学生通过观察、分析获取有用的信息，并据此逐步回答有关问题.学会从图象中提取有用的关键信息，数形结合，建立一次函数模型解决实际问题.七年级学生在12～13岁，有一定生活经验和较强的好奇心、求知欲，已具备了思维的完整性、深刻性和实践性等思维品质，但抽象思维尚待提高，抽象概括能力有限．在学习过程中尽可能地为学生提供更广阔的独立自由思考的空间，也鼓励学生大胆探索，调动学生的学习积极性，使学生在活动中学会解决问题的方法[1].

4教学目标

新课标导向的四维目标：

①通过函数图象读取信息并解决简单实际问题；

②理解一次函数解析式中k，b的实际意义；

③体会函数与方程的关系，感受数形结合、数学建模思想

④体会数学的实际应用价值，形成保护环境的意识，感受拼搏进取的精神.

5教学重难点

教学重点：通过分析一次函数图象所给的信息，提取关键信息，基于数形结合建立一次函数模型，解决简单的实际问题.

教学难点：建立一次函数模型解决实际问题，体会函数与方程的关系，发展“数形结合”的思想.

6教学过程

6.1温故知新

一次函数的图象经过A（0，1200），B（50，200）两点.求这个一次函数的解析式.

6.1.1游戏热身，判断对错

请两位同学到讲台上进行希沃课堂游戏PK判断对错，其他同学观看PK，并积极思考四道判断题.

①函数y=x-2的图象，y随x的增大而增大 （）

②函数y=x-2的图象与y轴交于（-2，0） （）

③函数y=x-2的图象与x轴交于（2，0） （）

④函数y=x-2的图象是一条过（3，-1）的直线 （）

6.1.2待定系数法求一次函数的表达式

一次函数的图象经过A（0，1200），B（50，200）两点.求这个一次函数的解析式.

设计意图利用游戏复习一次函数的性质，调动学生参与热情.复习待定系数法确定一次函数表达式，另外本表达式在新课学习中要用到，为新课学习作铺垫，埋下彩蛋.

6.2情境引入，新知探究

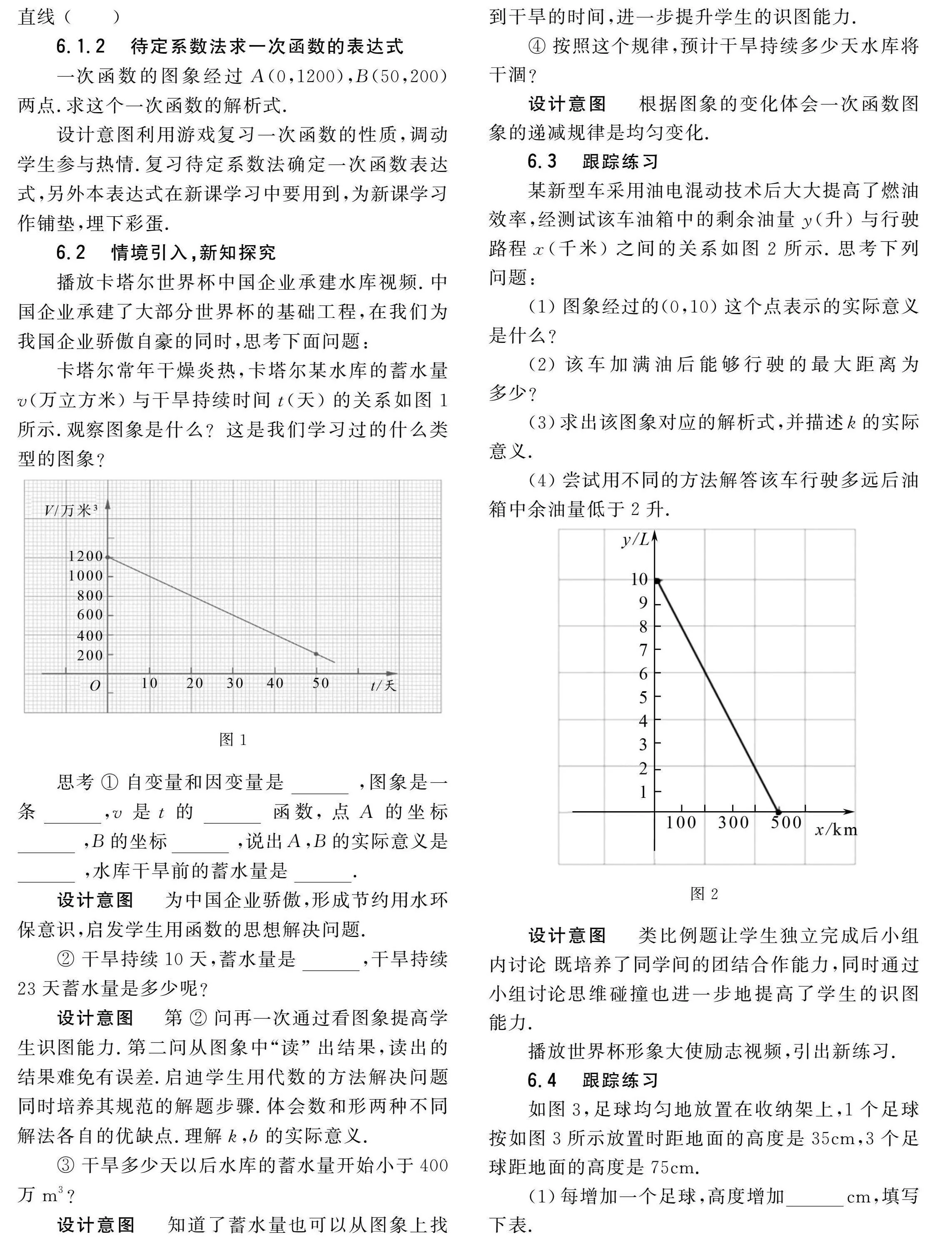
播放卡塔尔世界杯中国企业承建水库视频.中国企业承建了大部分世界杯的基础工程，在我们为我国企业骄傲自豪的同时，思考下面问题：

卡塔尔常年干燥炎热，卡塔尔某水库的蓄水量v（万立方米）与干旱持续时间t（天）的关系如图1所示.观察图象是什么？这是我们学习过的什么类型的图象？

思考①自变量和因变量是，图象是一条，v是t的函数，点A的坐标，B的坐标，说出A，B的实际意义是，水库干旱前的蓄水量是.

设计意图为中国企业骄傲，形成节约用水环保意识，启发学生用函数的思想解决问题.

②干旱持续10天，蓄水量是，干旱持续23天蓄水量是多少呢？

设计意图第②问再一次通过看图象提高学生识图能力.第二问从图象中“读”出结果，读出的结果难免有误差.启迪学生用代数的方法解决问题同时培养其规范的解题步骤.体会数和形两种不同解法各自的优缺点.理解k，b的实际意义.

③干旱多少天以后水库的蓄水量开始小于400万m3？

设计意图知道了蓄水量也可以从图象上找到干旱的时间，进一步提升学生的识图能力.

④按照这个规律，预计干旱持续多少天水库将干涸？

设计意图根据图象的变化体会一次函数图象的递减规律是均匀变化.

6.3跟踪练习

某新型车采用油电混动技术后大大提高了燃油效率，经测试该车油箱中的剩余油量y（升）与行驶路程x（千米）之间的关系如图2所示.思考下列问题：

（1）图象经过的（0，10）这个点表示的实际意义是什么？

（2）该车加满油后能够行驶的最大距离为多少？

（3）求出该图象对应的解析式，并描述k的实际意义.

（4）尝试用不同的方法解答该车行驶多远后油箱中余油量低于2升.

设计意图类比例题让学生独立完成后小组内讨论 既培养了同学间的团结合作能力，同时通过小组讨论思维碰撞也进一步地提高了学生的识图能力.

播放世界杯形象大使励志视频，引出新练习.

6.4跟踪练习

如图3，足球均匀地放置在收纳架上，1个足球按如图3所示放置时距地面的高度是35cm，3个足球距地面的高度是75cm.

（1）每增加一个足球，高度增加cm，填写下表.

（2）求y关于x的解析式;

（3）若最顶部足球距地面135cm，则该收纳架共放置几个足球？

设计意图此题由课本课后习题羽毛球问题自创改编.学生可以通过理解分析列出一次函数表达式.个别同学会用没有学过的二元一次方程组求解析式，这对学生是一种挑战.本题设置的目的在于，让学生明白当我们的实际问题没有图象时，我们可以建立一次函数模型解决问题，培养学生数学建模的能力.

6.5 新知探究

一次函数y=0.5x+1的图象如图4所示，

（1）y=0.5x+1与x轴的交点横坐标是？

（2）方程0.5x+1=0的解是？

（3）一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系？

设计意图通过观察、类比进一步体会函数与方程、数与形的关系，顺利地突破难点.建立了良好的知识体系.

6.6跟踪练习

（1）一次函数y=ax+b的图象如图5所示，则方程ax+b=0的解是？

（2）如图6，直线y=kx+b过点A（2，3），则方程kx+b=3的解是？

设计意图基于典型的习题，帮助学生进一步突破本节的重难点：函数与方程，数与形的关系.

6.7畅谈收获

设计意图让学生各自回忆本节课的各个环节，述说不同的收获，相互赏识共同提高.在反思过程中形成知识网络，理顺本节课的学习内容，抓住本节的重、难点，达到对一次函数图象应用能力的再提升.

6.8堂清测验

图7所示为试验田中某品种玉米的平均高度y（m）随试验田每公顷喷洒的农药质量x（kg）变化的图象.经研究发现，当该品种玉米的高度为1.25m时产量达到最高.求要让玉米产量最大，每公顷喷洒农药的量控制在多少.

设计意图针对本节课的重难点进行检测，做到有的放矢，为今后的教学打下坚实的基础.

6.9布置作业

设计意图分层作业，巩固并拓展新知，让学生得到不同层次的提高，达到因材施教的目的.

7结语

我们假设学习成绩是时间的一次函数，k表示学习态度，b表示基础，如果同学们都有正向积极的k，那么不管你的基础b如何，你的学习成绩就一定会像这刚劲的直线上升、上升、再上升！运用函数图象形象地呈现付出与勤奋两者之间的变化规律，激励孩子不断向上.课前课后呼应，使得整堂课更加完整和谐.

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020：4-7.