巧用图象法求一元二次方程的近似根

【摘要】一元二次方程在数学中占据了重要的地位，是初中数学的重要内容．对于求解一元二次方程，通常使用公式法或配方法．然而，有时候这些方法可能不适用，或者需要大量的计算．在这种情况下，可以尝试用图象法求出一元二次方程的近似根．本文介绍如何巧用图象法求一元二次方程的近似根．

【关键词】初中数学；图象法；一元二次方程

用图象法求解一元二次方程的近似根，是快速处理数学问题的方法之一．根据一元二次方程写出对应的函数表达式，在平面直角坐标系中画出函数图象，根据函数图象，找到根的可能位置，观察根附近的函数值，确定根的近似值．

1探索规律找解法

例1方程2x2+x－2=0的近似根可以看作是下列哪两个函数图象交点的横坐标（）

（A）y=2x2和y=x－2．

（B）y=2x2+x和y=2．

（C）y=2x2－2和y=x．

（D）y=－2x2和y=x+2．

解析由2x2+x－2=0得2x2=－x+2，则方程可看作函数y=2x2和y=－x+2的图象的交点，故（A）错误；由2x2+x－2=0得2x2+x=2，则方程可看作函数y=2x2+x和y=2的图象的交点，故（B）正确；由2x2+x－2=0得2x2－2=－x，则方程可看作函数y=2x2－2和y=－x的图象的交点，故（C）错误；由2x2+x－2=0得－2x2=x－2，则方程可看作函数y=－2x2和y=x－2的图象的交点，故（D）错误．

点评本题考查了一元二次方程与二次函数的关系，正确变形是关键．通过本例可以看出，一元二次方程的近似根可通过作函数图象的方法求解．

2在解题中深化解法

例2小朋在学习过程中遇到一个函数y=12xx－32．

（1）当x≥0时，y与x的几组对应值如表1，结合表1，画出当x≥0时，函数y=12xx－32的图象；

（2）若关于x的方程12xx－32=kx－1有一个实数根为2，则该方程其他的实数根约为（结果保留小数点后一位）．

解析（1）根据列表，描点连线，如图1.

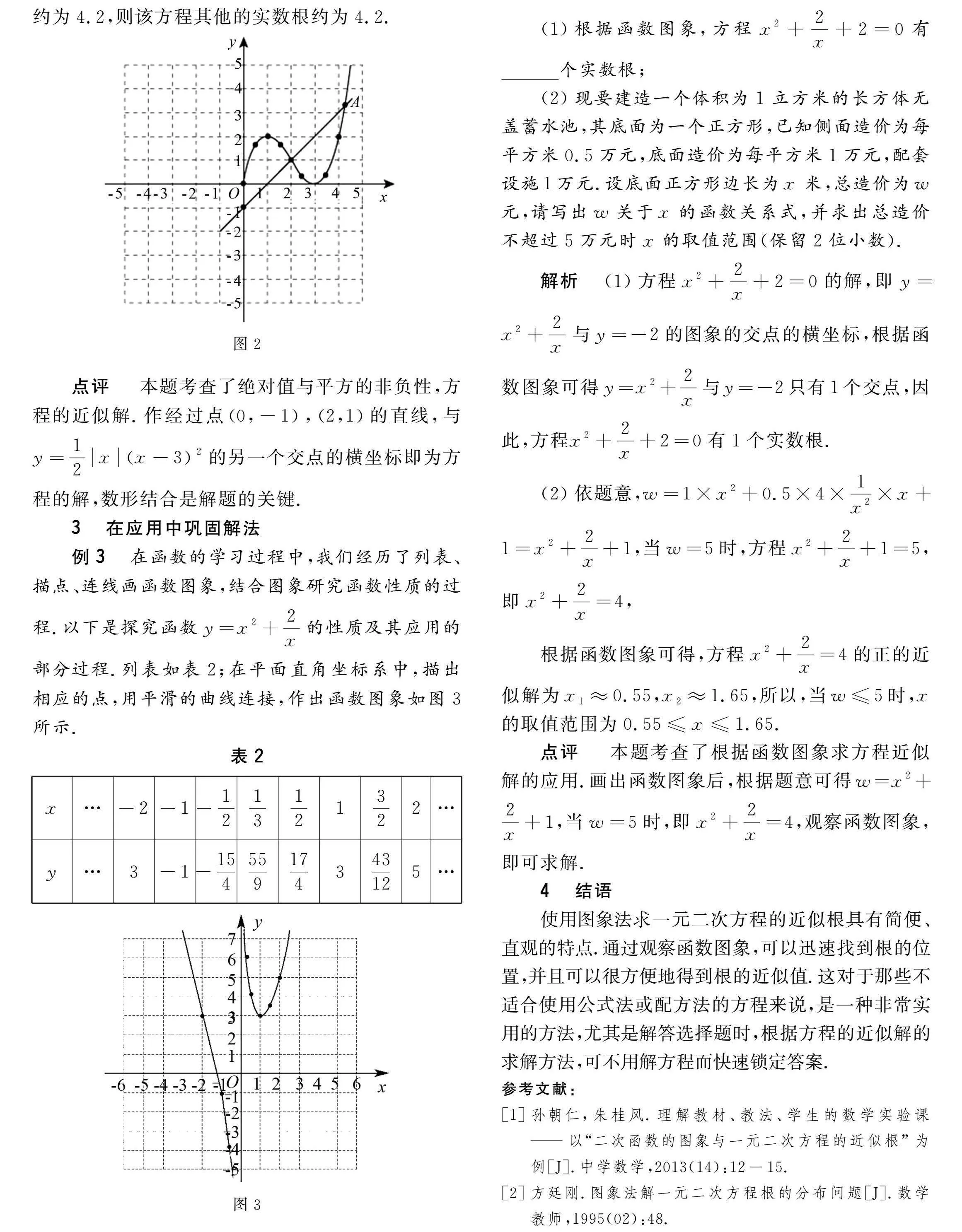
（2）依题意，12xx－32=kx－1有一个实数根为2，则过点2，1，12xx－32=kx－1的解即为y=12xx－32与y=kx－1的交点的横坐标，且y=kx－1过点0，－1，如图2，作过点0，－1，2，1的直线，与y=12xx－32交于点A，根据函数图象的交点可知点A的横坐标约为4.2，则该方程其他的实数根约为4.2．

点评本题考查了绝对值与平方的非负性，方程的近似解．作经过点0，－1，2，1的直线，与y=12xx－32的另一个交点的横坐标即为方程的解，数形结合是解题的关键．

3在应用中巩固解法

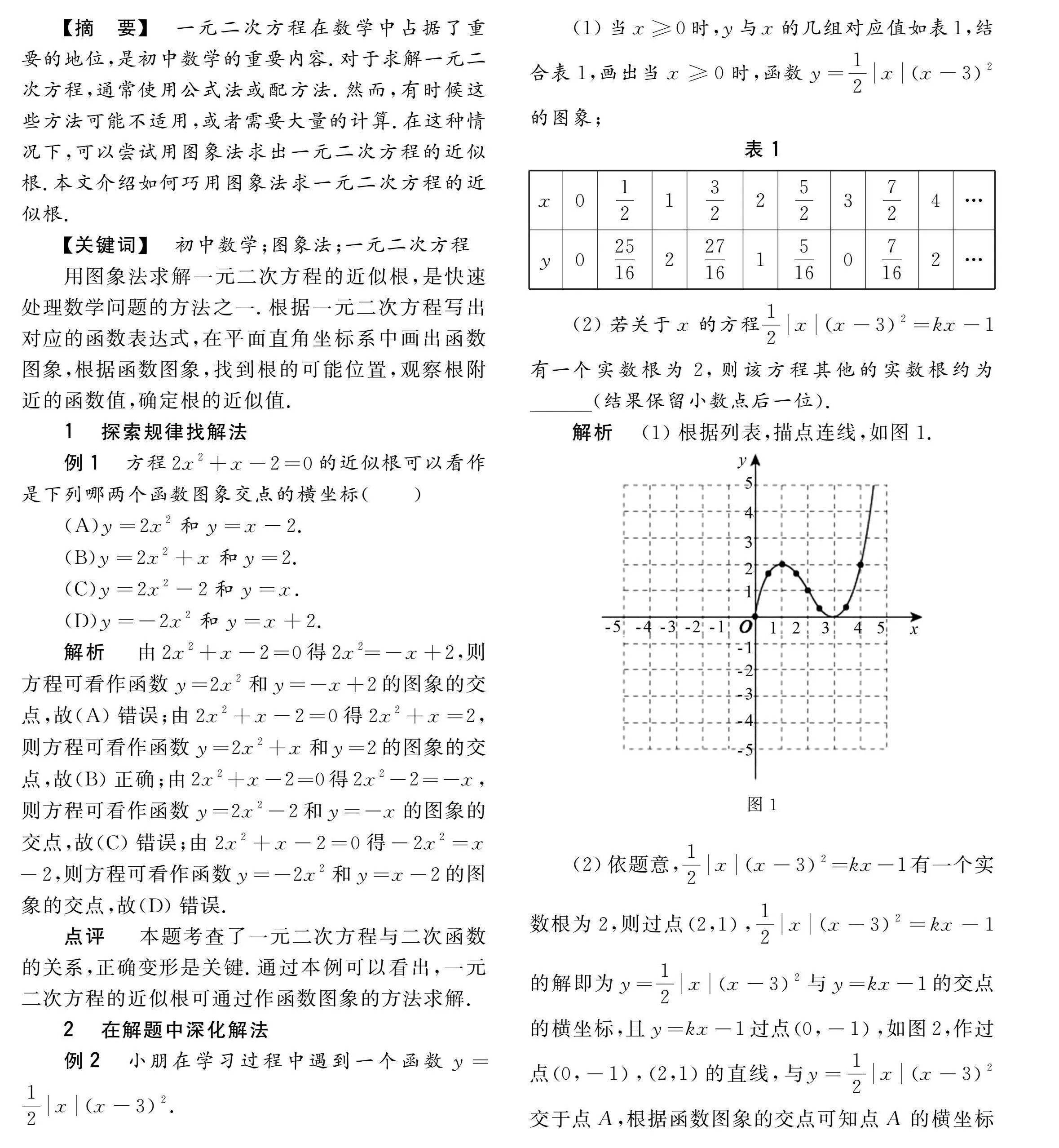
例3在函数的学习过程中，我们经历了列表、描点、连线画函数图象，结合图象研究函数性质的过程．以下是探究函数y=x2+2x的性质及其应用的部分过程．列表如表2；在平面直角坐标系中，描出相应的点，用平滑的曲线连接，作出函数图象如图3所示．

（1）根据函数图象，方程x2+2x+2=0有个实数根；

（2）现要建造一个体积为1立方米的长方体无盖蓄水池，其底面为一个正方形，已知侧面造价为每平方米0.5万元，底面造价为每平方米1万元，配套设施1万元．设底面正方形边长为x 米，总造价为w元，请写出w关于x的函数关系式，并求出总造价不超过5万元时x的取值范围（保留2位小数）．

解析（1）方程x2+2x+2=0的解，即y=x2+2x与y=－2的图象的交点的横坐标，根据函数图象可得y=x2+2x与y=－2只有1个交点，因此，方程x2+2x+2=0有1个实数根．

（2）依题意，w=1×x2+0.5×4×1x2×x+1=x2+2x+1，当w=5时，方程x2+2x+1=5，即x2+2x=4，

根据函数图象可得，方程x2+2x=4的正的近似解为x1≈0.55，x2≈1.65，所以，当w≤5时，x的取值范围为0.55≤x≤1.65．

点评本题考查了根据函数图象求方程近似解的应用．画出函数图象后，根据题意可得w=x2+2x+1，当w=5时，即x2+2x=4，观察函数图象，即可求解．

4结语

使用图象法求一元二次方程的近似根具有简便、直观的特点．通过观察函数图象，可以迅速找到根的位置，并且可以很方便地得到根的近似值．这对于那些不适合使用公式法或配方法的方程来说，是一种非常实用的方法，尤其是解答选择题时，根据方程的近似解的求解方法，可不用解方程而快速锁定答案．

参考文献：

[1]孙朝仁，朱桂凤.理解教材、教法、学生的数学实验课——以“二次函数的图象与一元二次方程的近似根”为例[J].中学数学，2013（14）：12-15.

[2]方廷刚.图象法解一元二次方程根的分布问题[J].数学教师，1995（02）：48.