反证法在初中平面几何解题教学中的应用

【摘要】平面几何在初中数学知识体系中占据重要地位．本文运用反证法从基本命题，位置关系，“至多”“至少”等形式的命题，否定性命题四个方面解初中平面几何题，同时对平面几何教学过程中应用反证法解题的策略进行总结，并从高度重视培养学生逆向思维、注重反证法方式方法、波利亚解题思想融入反证法教学角度，提出了相应的教学建议，打破学生固有的思维模式，锻炼其逻辑思维能力，不断提高逻辑推理与逆向思维能力．

【关键词】初中数学；反证法；平面几何；逆向思维

1引言

平面几何在中学课程内容模块“图形与几何”领域中占据核心地位，是学生学习数学的基础，有助于学生形成良好的数学思维和创新能力.反证法是一种常见的解题方法[3]，对于提高学生的数学应用能力、逻辑思维能力和创造性思维有显著作用.反证法的应用思路是假设命题结论是错误的，从这个假设出发通过推理进行论证，并根据已知条件和相关原则得出与已知事实相矛盾的结果，从而证明论题的正确性．故反证法是通过否定与命题相反的一面来证明事物的真实性，是一种间接的、让步的证明方法．反证法在平面几何解题中应用十分广泛[4]，在证明某些几何量之间的关系时，有助于从一个假设出发，通过逻辑推理揭示矛盾，从而验证原命题的正确性[5].

2反证法在初中平面几何解题教学中的具体应用

笔者将适用反证法证明的平面几何问题分为四类：基本命题、位置关系、“至多”“至少”等形式的命题、否定性命题，下面分别通过实例来说明反证法在初中平面几何中的应用．

2.1基本命题

在平面几何中，证明一些基本命题（学科中的初始命题）时，往往会由于缺少已有定理或命题的支撑而难以直接证明.此时，若运用反证法，从结论出发，否定原始结论以增加已知条件，可降低证明难度．

例1证明平行线性质定理：两条平行直线被第三条直线所截，同位角相等．

分析由题意可得，如图1所示，证明∠1=∠2．从正面直接证明是比较困难的，故考虑从问题的反面进行证明.先假设同位角∠1与∠2不相等，则可做出一个与∠1相等的角∠3，根据平行线的判定定理“同位角相等，两直线平行”，得到直线l1平行于直线l3，与“过直线外一点有且只有一条直线与已知直线平行”相矛盾.

小结平行线性质定理的证明是学生第一次接触到反证法在平面几何中的运用.题目所给条件太少，正向推导难，故尝试运用反证法.在教学过程中，注意启发学生遇到类似的初始命题时，学会多维度分析问题，正向思维不通，尝试从问题反面入手，判断哪些关键词需要改变，哪些关键词可作为证明时的条件．

2.2位置关系

在平面几何中判断点与线、线与线之间的位置关系时，往往有定义法和反证法两种方法，若用定义法难以直接证明，运用反证法则具有独特优势．

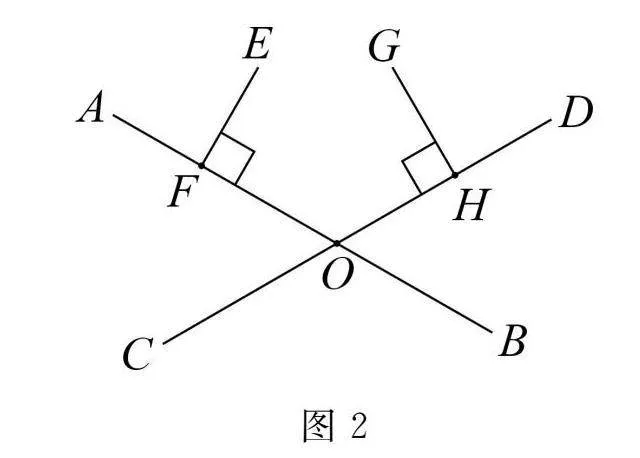
例2如图2，已知：直线AB与CD相交于O，EF⊥AB于点F，GH⊥CD于点H．求证：EF和GH必相交．

分析已知AB交CD于O，EF⊥AB于F，GH⊥CD于H，需证明EF与GH一定相交.貌似这是一个不需要证明便可得知的结论，但是正面难以证明，可考虑从结论入手，运用反证法进行求证．对结论进行反设，于是假设EF∥GH，则它们的垂线AB∥CD，与题设矛盾．

小结此类证明两几何量之间的位置关系的题目，运用定义法直接证明较为棘手，可联想到反证法，会使得证明更加简洁与高效．在反设时通常选择要求证的结论，即求题干的逆否命题为真命题，因此要明确两几何量之间可能存在的所有位置关系，否定了一种位置关系，其余的位置关系选择很重要．通过分析发现常规思维解决本题较为繁琐，而反证法恰好能规避许多麻烦.将题干中需要求证的结论进行反设，如若得出来的结论与条件不符，即与题干矛盾，从而得证. 在确定两几何量位置关系的教学过程中，要有意识启发学生从不同角度进行思考，帮助学生冲破常规思维模式的束缚.

2.3“至多”“至少”形式的命题

证明此类命题时，若从正面出发，需要分多种情况讨论，非常复杂，故首选反证法．例如当遇到“至少有一个元素具备某种性质”，若将此结论否定，便可得到“没有一个元素具备该性质”，用此否定论断进行证明会更加简便．

例3求证一个三角形中至少有一个内角大于或等于60°.

分析如图3，已知△ABC，题目可转化为求证：∠A，∠B，∠C中至少有一个角大于或等于60°．若从正面进行证明，“至少”这个条件将要求我们进行分类讨论，使得证明过程变得繁琐．于是可考虑运用反证法，将“至少有一个”反设为“一个都没有”，即假设三角形的三个内角都小于60°，则可得其内角和小于180°，与“三角形的内角和等于180°”相矛盾．

小结面对含有“至少”“至多”这类表范围和数量的词的问题，往往从反面进行证明，将其否定之后会使得应考虑的情况减少，从而更有利于证明．例如：本题中的“至少有一个”若从正面进行证明则要分为“有一个内角大于或等于60°”“有两个内角大于或等于60°”“有三个内角等于60°”这三种情况，而将其反设之后，只需证明“三个内角都小于60°”这一种情况．这种逆向思维的运用可化繁为简、化难为易，不仅提高了学生的解题速度，还在很大程度上提升了学生的逻辑思维能力.

2.4否定形式命题

结论中出现“不能……”“不是……”等形式的命题，称之为否定性命题．证明研究对象“不存在”或“不具有”某种性质时，通常用反证法进行证明．因为此类命题的论断不是特别明确，用直接法难以证明，而否定此类命题的结论就是肯定，相较于直接证明否定会比较简单．

例4如图4，在梯形ABCD中，AD‖BC，对角线AC与BD相交于P，过P作与梯形底边AD平行的直线，交AB于M，交CD于N．求证：MN不可能是梯形ABCD的中位线．

分析观察题目可知，该题为否定性命题的证明，采用反证法能使证明更简便．基于结论进行反设，得“MN是梯形ABCD的中位线”，由中位线的性质定理可知，点P为BD，AC的中点，由边角边得△PBC≌△PDA，所以AD=BC，这与梯形的定义相矛盾，得证．

小结否定性命题从正面证明难以找到公理、定理作为理论支撑，因此这类问题运用反证法便能迎刃而解．以本题为例，要证MN不是中位线，即可假设MN是中位线，由中位线这一条件一步步延伸推出矛盾得出结论，使得证明过程更加简洁、流畅．反证法在该种题型中的运用有效地简化了数学问题，提高了学生的解题效率，逆向思维的运用能提升学生的推理素养.

3教学建议

高度重视培养学生逆向思维 反证法是数学中至关重要的解题方法，反证法是间接证明法中的一种，在平面几何中，许多题目过于抽象或者几何图形不能被直观地表现出来，利用反证法解答此类问题，常常会事半功倍.因此，教师要提高自身对反证法的重视程度．教师要在初中阶段为学生夯实基础，注重培养学生的逆向思维，不断提高理解方式和思维方式．教师还要不断提升自身对反证法的数学知识与教学知识的理解与运用，注重与同事之间的合作交流以及对自身的教学反思．

注重反证法方式方法 反证法本身具有高度的抽象性，教师要合理运用生活实例引入反证法．若在数学教学过程中生硬地介绍反证法的理论并直接运用于解题过程中，会让学生学得莫名其妙．为了化“虚”为“实”，教师在教授反证法的时候，需要将课堂引入趣味化、生动化、形象化，有助于提升学生学习的积极性．例如，可引入“路边苦李”这一故事，教师可提问：“为什么路边随手摘的李子一定是苦的呢？”可引导学生从不同角度思考，让学生有豁然之感．接着进入反证法的归谬阶段，询问学生：从反面思考后，是否发现了与常识、事实相矛盾的地方？引导学生思考：如果李子是甜的，而且长在路边随手可摘，合理吗？让学生自主阐述不合理的地方．通过生活实例、理解应用不仅可以帮助学生更加容易理解反证法的本质，同时锻炼了学生的应用意识与实践能力．学生理解反证法本质后，应用解题时通过引导、讨论等，进一步加深学生知识理解，提高反证法应用能力，提升学生思维能力与创新意识．

波利亚解题思想融入反证法教学教师将波利亚解题思想融入反证法教学中，启发学生的解题思路.波利亚的解题思想强调从问题的本质出发，通过简化问题、探索普遍规律和利用数学中的启发法来寻找解题策略.将波利亚的解题思想应用在反证法解决平面几何问题中，促使学生更系统、更完整地解题.第一步，弄清题目，即教师在讲解题目时应引导学生分析题干，理解题意，明确问题，如前文例1；第二步，确定解题方案，引导学生思考解题时选择最优的方法，如前文例4；第三步，实施解题方案，确定运用反证法解题三部曲：反设、归谬、得出结论；第四步，回顾与反思，问题解决之后要及时进行验算，降低题目的出错率，并进行反思归纳，培养学生的迁移能力.

4结语

平面几何与反证法都是初中数学中不可或缺的一部分，本文概述了反证法和平面几何的相关内容，通过例题评析了反证法在初中平面几何中的应用，并给出了关于反证法在平面几何教学中的建议.学生使用反证法能简化难以直接证明的平面几何问题，提高解题效率，培养知识迁移能力，打破固有的思维模式，锻炼逻辑思维能力，不断提高逻辑推理与逆向思维能力．

【本文系国家级大学生创新创业训练计划项目“面向情绪脑电多域特征提取的张量分解算法研究”研究成果，课题编号：202310663051】

参考文献：

［1］王楠.初中平面几何问题的求解技巧分析[J].数理天地（初中版），2023（03）：27-28.

［2］刘宏仕.初中数学平面几何教学问题及对策研究[J].求知导刊，2024（01）：95-97.

［3］丁宝波.反证法的理论依据及其应用条件的探讨——中学数学中的应用[J].学周刊，2014（26）：215.

［4］马多贵.反证法在初中数学解题中的应用探讨[J].学周刊，2020（12）：96-97.

［5］满孝珍.反证法在初中数学证明题中的应用[J].数理化学习（初中版），2022（26）：26+29.

［6］周倩.基于波利亚解题思想解三角形内切正方形问题[J].学园，2018，11（14）：93-94+98.

[7]邰桂琴.例谈波利亚“怎样解题表”在初中数学解题教学中的运用[J].数理天地（初中版），2022（20）：2-3.