内流作用下深海扬矿硬管流固耦合振动特性数值仿真研究

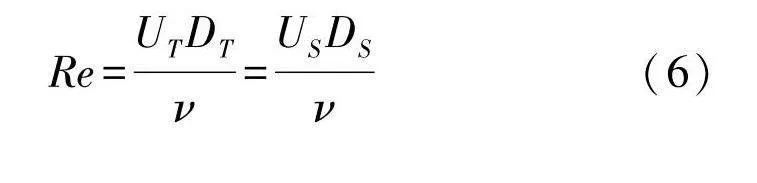
摘"要： 为研究内流作用下扬矿硬管的振动特性，根据相似理论建立包括扬矿硬管、中间仓、内部流场在内的流固耦合有限元模型，计算了扬矿管在内流场作用下的模态频率，并根据计算结果进行谐响应分析；探究了壁厚、内径、恒定内流流速、不同频率与幅值的脉动内流流速对扬矿管系统振动特性特别是共振行为的影响.结果表明：恒定内流流速下，扬矿管振动位移的频率与其振幅最大的共振频率（12阶固有频率）相一致，主要表现为纵向振动.距中间仓10 %管长范围内，扬矿管的振动幅值变化低于5 %.相对于保持壁厚不变调整内径，保持内径不变调整壁厚对扬矿管共振行为的抑制作用更为显著.脉动内流幅值大于0.5 m/s时，扬矿管的最大振动位移与等效应力接近线性增长.随着脉动内流频率的增加，存在以12阶固有频率为中心、区间长度为8 Hz的共振带，在共振带内，扬矿管的最大等效应力出现在顶端，沿水深方向逐渐减小.

关键词： 扬矿硬管；流固耦合；共振响应；有限元分析

中图分类号：O352"""文献标志码：A"""""文章编号：1673-4807（2024）04-016-09

Numerical simulation research on the fluid-solid coupling characteristicsof the lifting pipe under the influence of internal fluid

TIAN Shilei 1， 2， CHEN Ke 1， 2*，YOU Yunxiang 1， 2

（1.State Key Laboratory of Ocean Engineering， Shanghai Jiao Tong University， Shanghai 200240， China）

（2.Yazhou Bay Institute of Deepsea Technology， Shanghai Jiao Tong University， Sanya 572000， China）

Abstract：In order to research the vibration characteristics of the lifting pipe under the effect of internal flow， the fluid-solid coupling finite element model including the lifting pipe， the intermediate warehouse and the internal flow field is established according to the similarity theory， and the modal frequency of the lifting pipe under the effect of the internal flow field is calculated， and the harmonic response analysis carried out according to the calculation results. The effects of wall thickness， inner diameter， constant internal flow velocity， pulsating internal flow velocity with different frequencies and amplitudes on the vibration characteristics， especially the resonance behavior of the lifting pipe system are investigated. The results show that the frequency of the vibration displacement of the lifting pipe is consistent with the resonance frequency （12th order natural frequency） with the largest amplitude at a constant internal flow velocity， and the vibration is mainly longitudinal. Within 10% of the pipe length near the intermediate warehouse， the change in vibration amplitude of the lifting pipe is less than 5%. Compared with adjusting the inner diameter while keeping the wall thickness unchanged， adjusting the wall thickness while keeping the inner diameter unchanged has a more significant inhibition effect on the resonance behavior of the lifting pipe. When the amplitude of pulsating internal flow is greater than 0.5 m/s， the maximum vibration displacement and equivalent stress of the lifting pipe increase linearly. With the increase of the frequency of pulsating internal flow， there is a resonance band with a width of 8 Hz centered on the 12th order natural frequency. Within the resonance band， the maximum equivalent stress of the lifting pipe appears at the top and gradually decreases along the water depth direction.

Key words：lifting pipe， fluid-structure interaction， resonance response， finite element analysis

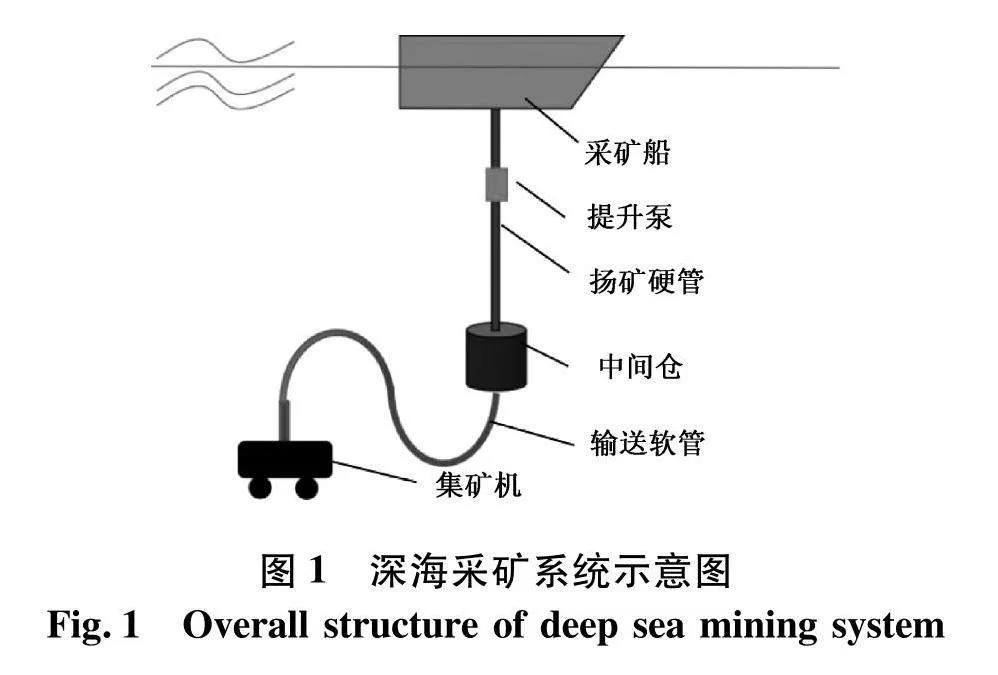
海洋中蕴含着丰富的矿产资源，其中最具有开发前景的矿产资源包括富钴结壳、多金属结核、多金属硫化物等稀有金属矿物资源，未来可有效替代日渐枯竭的陆地矿产资源［1］.自20世纪60年代以来，美国、德国、英国、日本、韩国、印度等国先后对深海矿产资源进行勘探，研发开采设备，多次开展单体以及综合的海上试验，具体包括：水力提升系统海试、集矿机拖航试验、集矿机行走试验、集矿机采集与水力提升试验等［2］.历经数十年的技术沉淀，国内外科研人员开发了4种比较典型的开采系统：拖斗式采矿系统、连续斗绳式采矿系统、穿梭艇式开采系统以及管道提升式采矿系统［3］.目前，管道提升深海采矿系统是在工业实践中认可度最高的开采系统［4］.

管道提升深海采矿系统的示意图如图1，具体组成包括：采矿船、提升泵、扬矿硬管、中间仓、输送软管、集矿机等.其中，扬矿硬管长达上千米，上端通过升沉补偿装置与采矿船相连，下端通过中间仓与柔性软管相连.由于软管刚度偏小，且有浮力材料支撑，其对扬矿管的作用力可以忽略，可将扬矿管简化为下端悬挂重物的悬臂管.扬矿管是整个采矿系统中最为薄弱的环节［5］，在内部流体作用下会产生流固耦合振动.特别是与一般海洋油气立管相比，深海采矿扬矿管的内流流速更大，更易对管道的位移与应力产生不可忽略的影响［6］.当外界激励频率与扬矿管固有频率相接近时，易引起管道的共振，导致管道产生较大应力、应变，甚至造成采矿系统失效，引发灾难性事故［7］".因此，准确分析预报扬矿管在内部流场作用下的流固耦合振动特性，特别是在内部流体激励下的共振行为，具有重要的研究价值.

针对输流管道的流固耦合振动特性，以往学者虽然做了诸多研究，但多集中于水平输送、两端支撑的管道［8-10］，对于一端支撑的悬臂管研究较少.文献［11］基于Newmark方法针对深水立管建立非线性耦合动力学方程分析其横向与纵向运动情况；文献［12］基于谐波微分求积法分析了上端固支悬臂管在内流场作用下的振动问题；文献［13-14］采用有限元法分析了不同内流流速与内流密度对柔性立管在非均匀外流下的流固耦合振动特性的影响.文献［15］设计了一套针对管道输送系统的振动测试装置，对不同输送浓度下管道的振动位移进行时域分析与频域分析；文献［16］通过建立扬矿硬管振动试验系统分析了在锰结核泵工作产生的动载荷作用下扬矿管的弯曲及扭转振动特性;李艳等［6］基于有限元软件ANSYS Workbench分析了内外恒定流速、内流密度对扬矿硬管流固耦合力学特性的影响；文献［17］利用ABAQUS软件计算了不同中间仓质量时扬矿管的固有频率，研究了不同采矿船升沉频率、升沉幅值对阶梯扬矿管纵向振动位移与轴向力的影响；文献［18］基于软件ANSYS Workbench对不同约束条件下的扬矿管进行预应力模态分析以及谐响应分析，并基于分析结果优化了扬矿管结构.

目前关于内流参数变化对扬矿管的振动特性特别是共振现象的研究尚不充分.因此，文中以扬矿硬管系统为研究对象，基于有限元以及相似理论建立扬矿硬管、中间仓与管内流体的流固耦合模型，计算扬矿管在内流场作用下的固有频率以及振幅最大的共振频率，分析不同管壁厚度、内径对扬矿管固有频率、位移、应力特性的影响；同时分析内流场不同恒定流速、不同频率与幅值的脉动流速对扬矿管的流固耦合振动特性特别是共振行为的作用效果，为扬矿管系统设计以及振动控制提供参考.

1"流固耦合数学模型及相似理论

1.1"流体域控制方程

流体流动要符合质量守恒、动量守恒等定律，可由连续方程及动量方程来描述.

连续方程：

ρt+（ρux）x+（ρuy）y+（ρuz）z=0（1）

式中：ρ为流体密度；t为时间；ux、uy、uz分别为流体速度在3个坐标上的分量.

动量方程：

tρv+SymbolQC@·ρvv=-SymbolQC@p+SymbolQC@·μSymbolQC@v+SymbolQC@vT+ρg+F （2）

式中：p为压力；v为流体速度；μ为粘性系数；g为重力加速度；F为源项.

1.2"固体振动控制方程

Mx··+Cx·+Kx=F（3）

式中：M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵；F为外载荷；x为管道振动位移.

1.3"流固耦合守恒方程

流固耦合分析满足基本的守恒原则，流体与固体求解所涉及的力、位移、速度等信息在流固耦合交界面处相等.

位移协调方程：

df=ds（4）

力平衡方程：

τf·nf=τs·ns（5）

式中：f表示流体；s表示固体；d表示位移；τ表示应力.

1.4"相似理论

对1 000 m长的扬矿管进行数值模拟研究，其超长细比特性会导致建模产生数百万的网格，极大消耗计算资源.因此，有必要根据相似理论［19］对扬矿管系统的长度与直径按不同比例进行缩比计算，降低扬矿管系统的长细比，进而降低网格分辨率，将网格数量限定在十万量级，大幅减少计算资源消耗；同时保证有限元模型与真实扬矿管系统结构相似及雷诺相似.

根据文献［19］，对扬矿管的主要影响参数（截面积之比、长度之比、杨氏模量之比）按比例因子进行放缩，可实现扬矿管与模拟管道的几何相似、弯曲变形相似、拉伸变形相似，设计出与真实扬矿管系统相似的有限元模型管道.在文中，截面积之比CD取0.05，长度之比CL、弹性模量之比Ce均取0.005.

此外，有限元模型应与真实扬矿管满足流场相似，即雷诺相似.雷诺相似定律表达为：

Re=UTDTν=USDSν（6）

式中：T为真实扬矿管系统中的参数；S为有限元模拟系统中的参数；U为进流速度；D为输流管道内径；ν为流体运动粘性系数.

由于真实扬矿管的合理流速约为3 m/s［6］，且在现有研究成果中扬矿管内径存在差别，本文根据雷诺相似定律并结合深海采矿实际情况将内流流速变化区间确定为0～12 m/s，探究不同内流流速下扬矿管的振动特性.

2"扬矿管流固耦合模型的建立

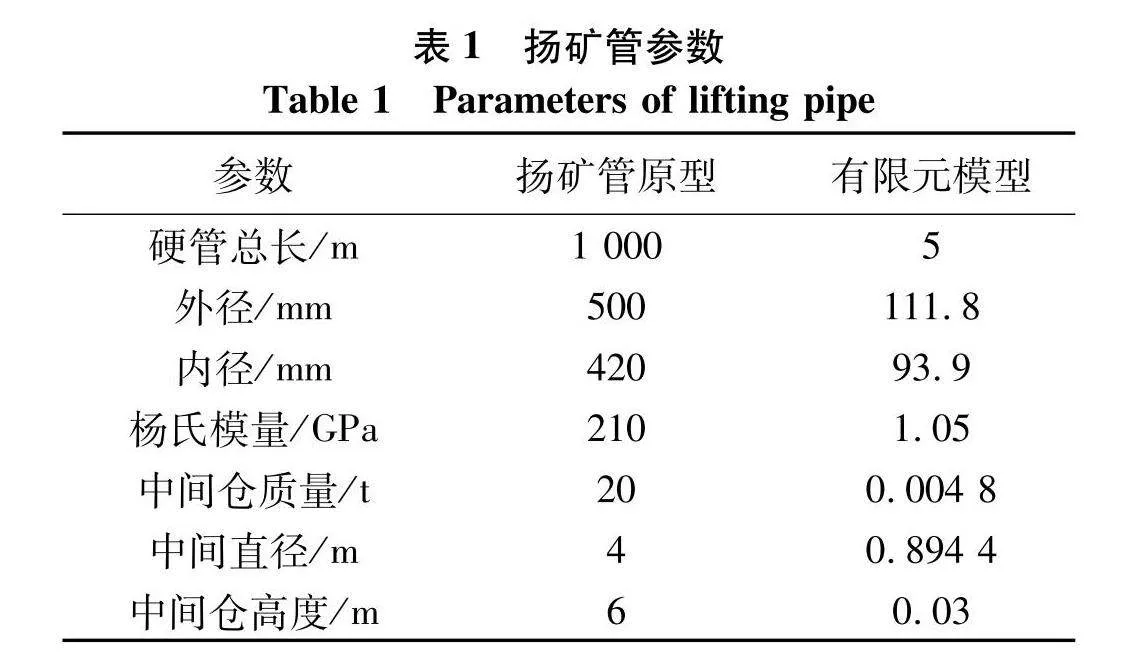
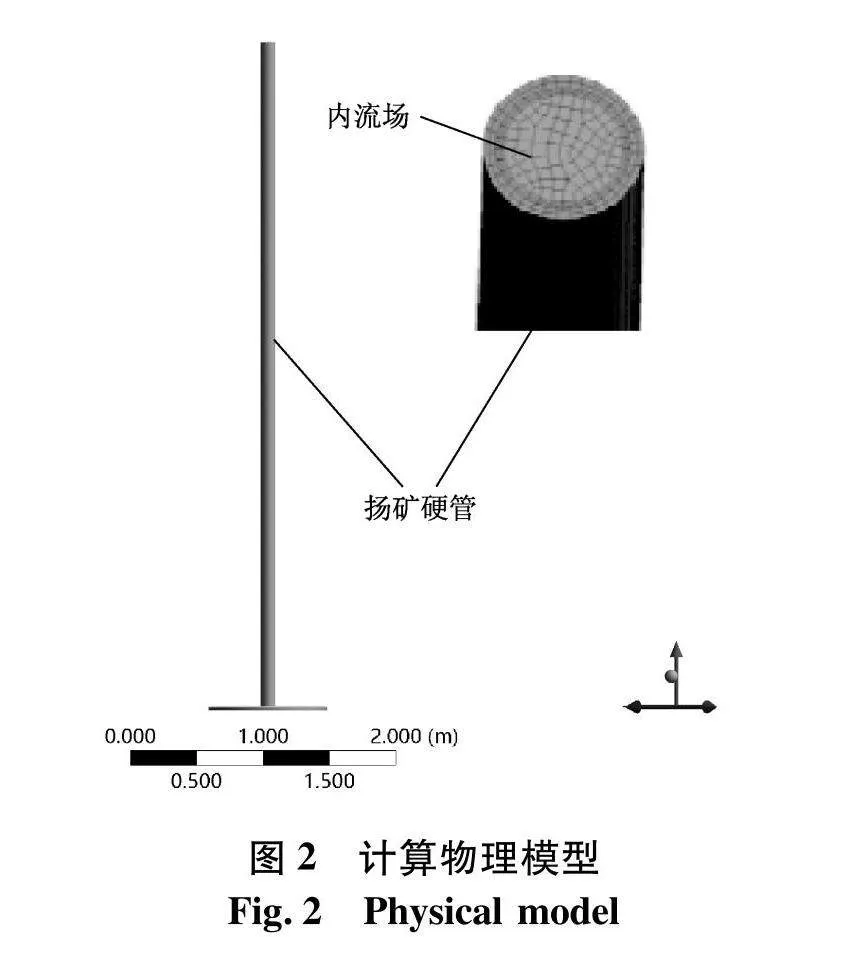
基于ANSYS Workbench在直角坐标系下建立扬矿硬管系统及内部流体的三维实体模型，分析不同工况下扬矿硬管的流固耦合振动特性.扬矿硬管系统由扬矿管与中间仓组成，管道上端采用固定支撑，下端与中间仓相连，作为自由端，其有限元模型如图2.管道材料采用结构钢，泊松比取0.3，密度为7 850 kg/m3.根据前述相似比，扬矿硬管系统及其对应有限元模型的物理参数如表1［15］.假定管内流体为不可压缩粘性流体，密度为1 123 kg/m3，流体粘度为3×10-3 Pa·s.

根据表1参数，采用六面体单元对扬矿硬管系统及其内部流体进行网格划分.其中，扬矿管与中间仓的网格共计43 111，内流场网格为46 872.施加重力载荷，设置重力加速度为9.81 m/s2，并将浮力以载荷形式施加到扬矿管系统模型中.模型管道入口（下端）设置为速度入口，出口设置为压力出口，管道内壁面设为无滑移边界条件.由于湍流状态下的管道流动问题通常采用雷诺时均（RANS）湍流模型进行求解［20］，故文中采用雷诺时均湍流模型中的Realizable k-ε模型求解扬矿管内流体控制方程.

3"扬矿管模态分析

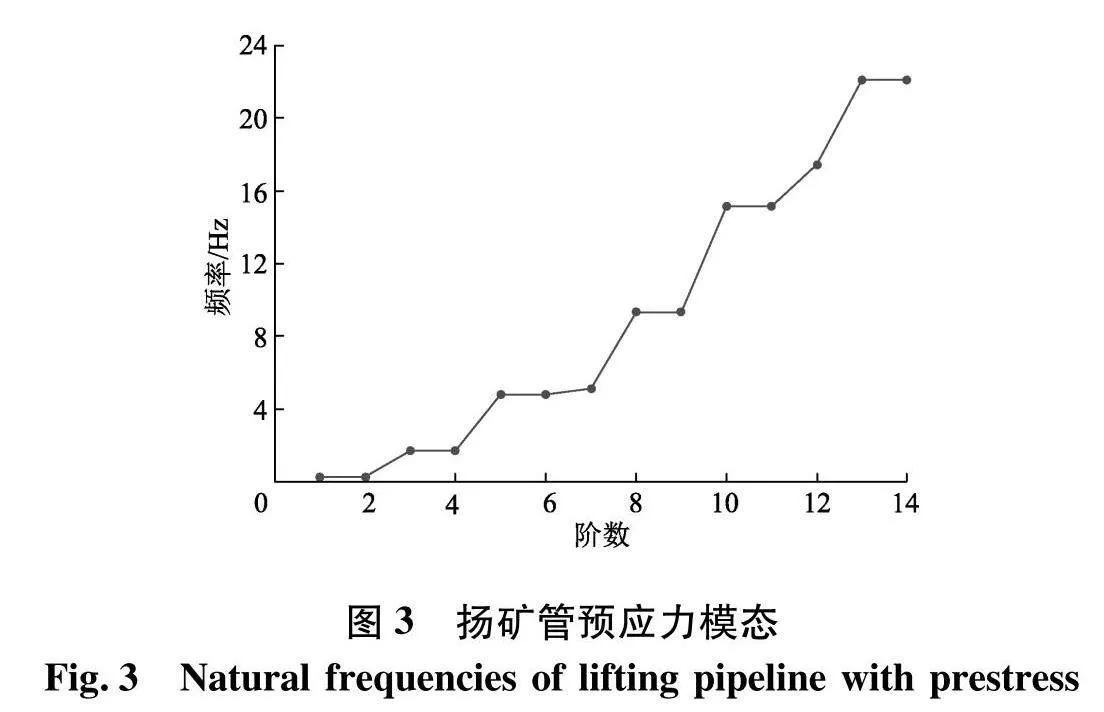
为避免扬矿管因内流激励频率与其固有频率相近而导致共振现象，对扬矿管在预应力下的模态频率进行分析.设置入口流速为12 m/s，将流场求解所得载荷以预应力的形式施加到管道内表面上，计算扬矿管的固有频率及振型.由于在结构振动时产生主要影响的是低阶模态，所以文中主要研究扬矿管前14阶固有频率，模态分析所得各阶频率如图3.

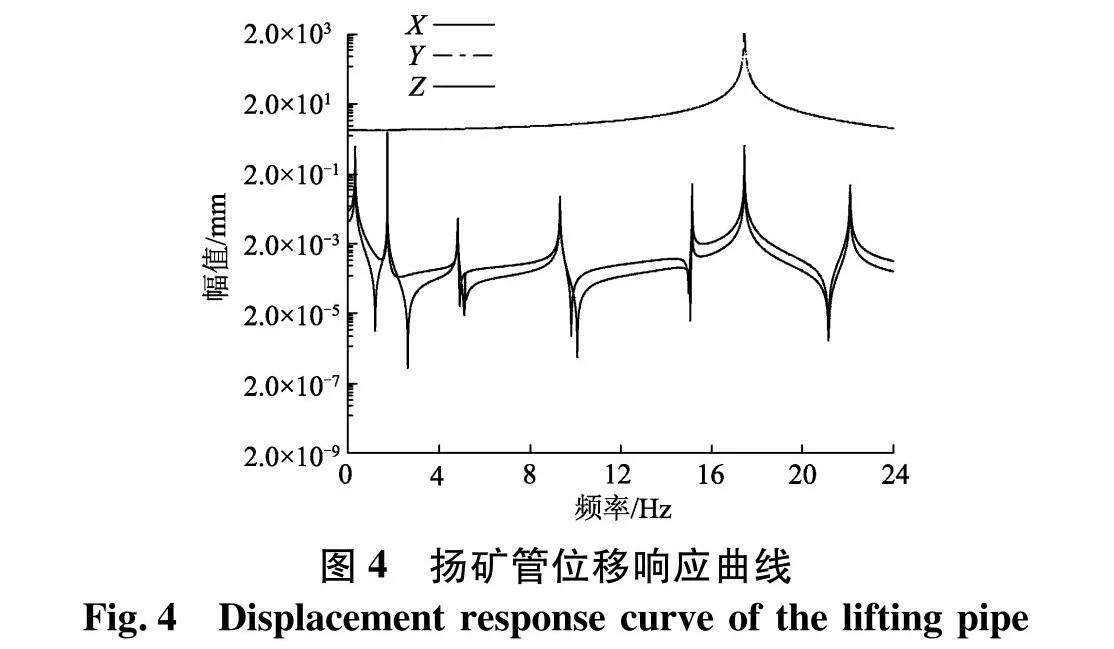
基于图3模态分析结果进行谐响应分析，对扬矿管内壁面施加频率不断变化的周期正弦载荷激励，扬矿管在X、Y、Z三个方向的位移频率响应如图4，图中纵轴采用对数坐标.由图4可知，随着激励频率的增加，扬矿管在各方向上相继出现峰值，峰值位置与扬矿管预应力下的2阶（0.305 Hz）、4阶（1.688 Hz）、6阶（4.777 Hz）、9阶（9.284 Hz）、10阶（15.1 Hz）、12阶（17.443 Hz）、14（22.052 Hz）阶模态频率相对应；扬矿管在X、Z方向上的位移响应值具有对称性，且远小于Y方向上的响应值；在频率为17.4 Hz时，扬矿管位移在各个方向均达到峰值，这一频率与扬矿管第12阶预应力模态相对应，振型表现为纵向振动；当这一频率与外界激励频率相接近时会导致振幅最大的共振现象.

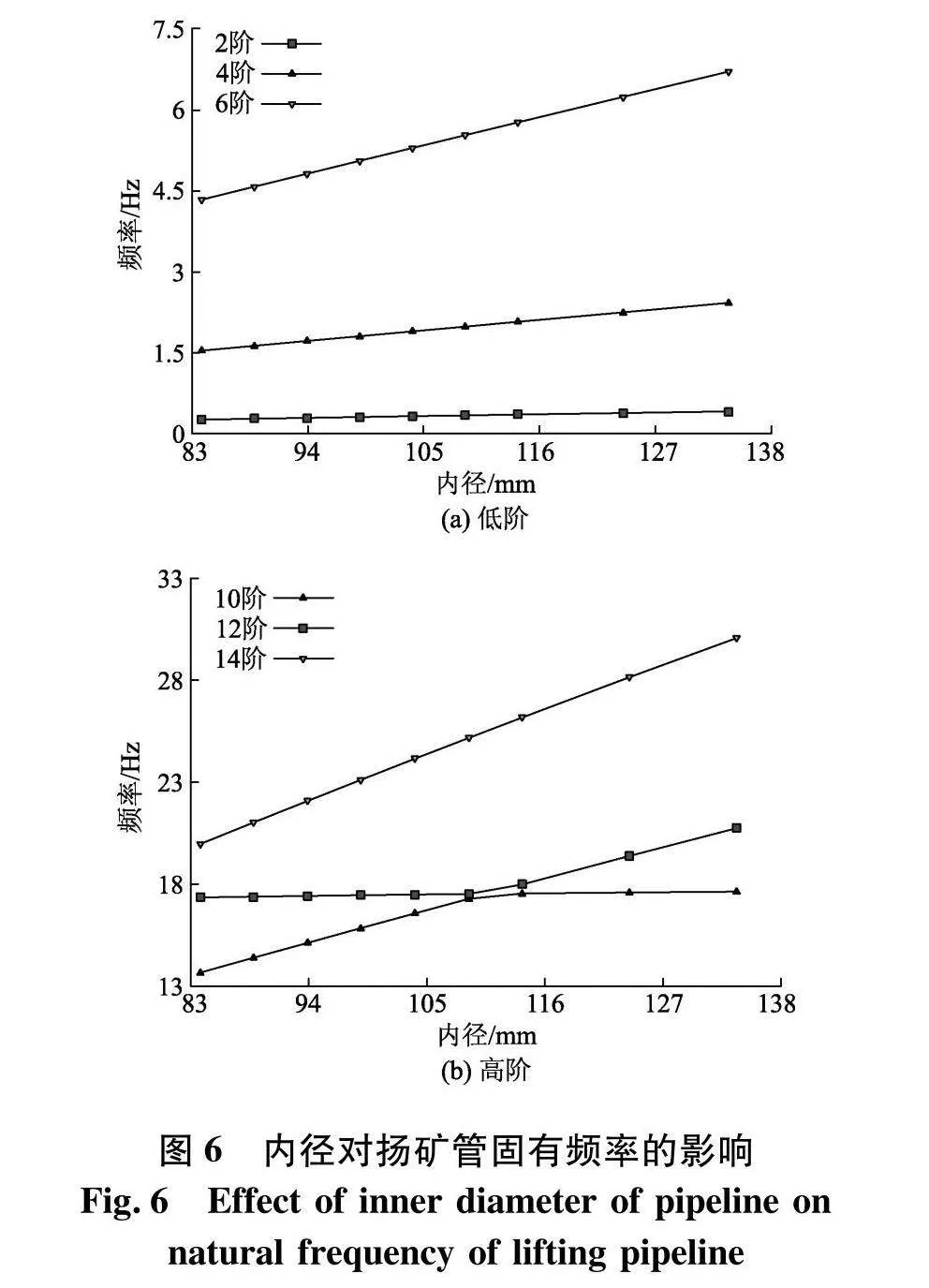
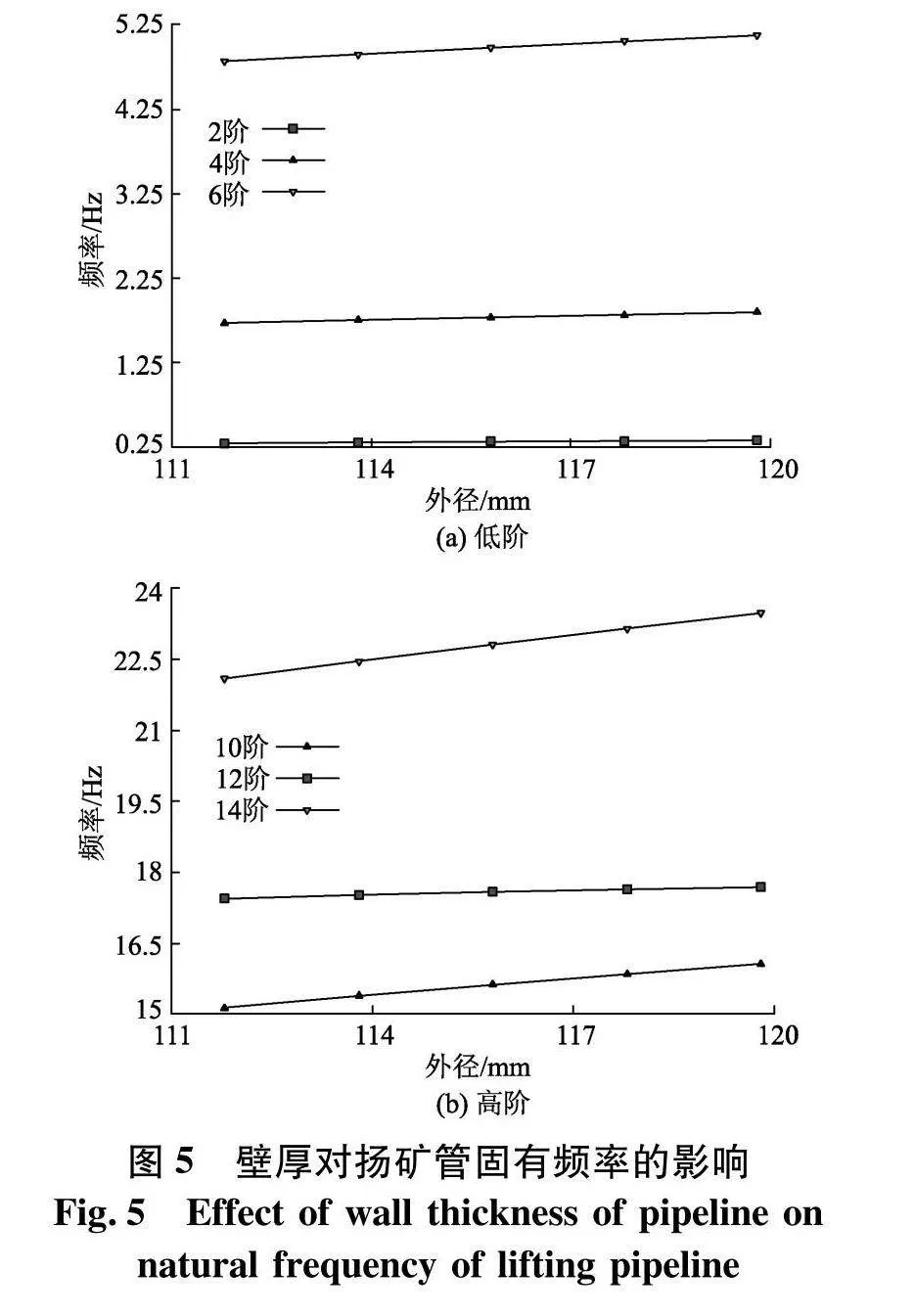
为优化扬矿管设计，在一定范围内避免扬矿管与管内流体的共振，对不同壁厚、内径条件下扬矿管的预应力模态进行分析.入口流速取12 m/s，保持内径不变，以2 mm的间隔增加外径，计算壁厚的增加对扬矿管预应力下模态的影响，计算结果如图5.保持壁厚不变，计算内径从83.9 mm增加到133.9 mm过程中扬矿管的固有频率，结果如图6.根据前文谐响应分析所得峰值对应频率的阶数，提取不同壁厚、内径条件下的扬矿管第2、4、6、10、12、14阶预应力模态频率进行分析.由图5，扬矿管壁厚的增加对扬矿管各阶固有频率均有提升作用.保持内径不变，外径从111.8 mm增加到119.8 mm，14阶固有频率提升了1.397 Hz，2阶固有频率提升了0.03 Hz；在壁厚等间隔增加的过程中，12阶固有频率依次增加了0.08、0.064、0.052、0.048 Hz；说明相对于低阶频率，增加壁厚对高阶频率提升作用更为显著，壁厚的等幅增加对12阶固有频率的提升作用逐渐降低.

综合上述分析结果可知，扬矿管在12阶固有频率处发生共振现象时，振幅最大，此时扬矿管表现为纵向振动；可通过提高扬矿管的壁厚、内径可以改变其固有频率，在一定范围内避免共振现象的发生.

4"扬矿管流固耦合振动响应分析

可通过瞬态流固耦合方法对扬矿管在内流场作用下的振动特性进行时域分析.流固耦合按在耦合交界面的数据传递方式可分为单向流固耦合与双向流固耦合.单向流固耦合是指同一时间步内，流体求解器计算的载荷单向传递给固体求解器，不计入结构形变对流场的影响；双向流固耦合是指同一时间步内，流体求解器与固体求解器数据双向传递，考虑流体与结构的相互影响.由于双向流固耦合计算周期长且不适用于结构变形较大的情况，单向流固耦合可以满足计算精度和准确性的要求，所以本研究采用单向瞬态流固耦合分析方法求解在不同恒定流速以及不同频率、幅值的脉动流速下扬矿管的流固耦合振动特性.

4.1"恒定流速对扬矿管振动特性的影响

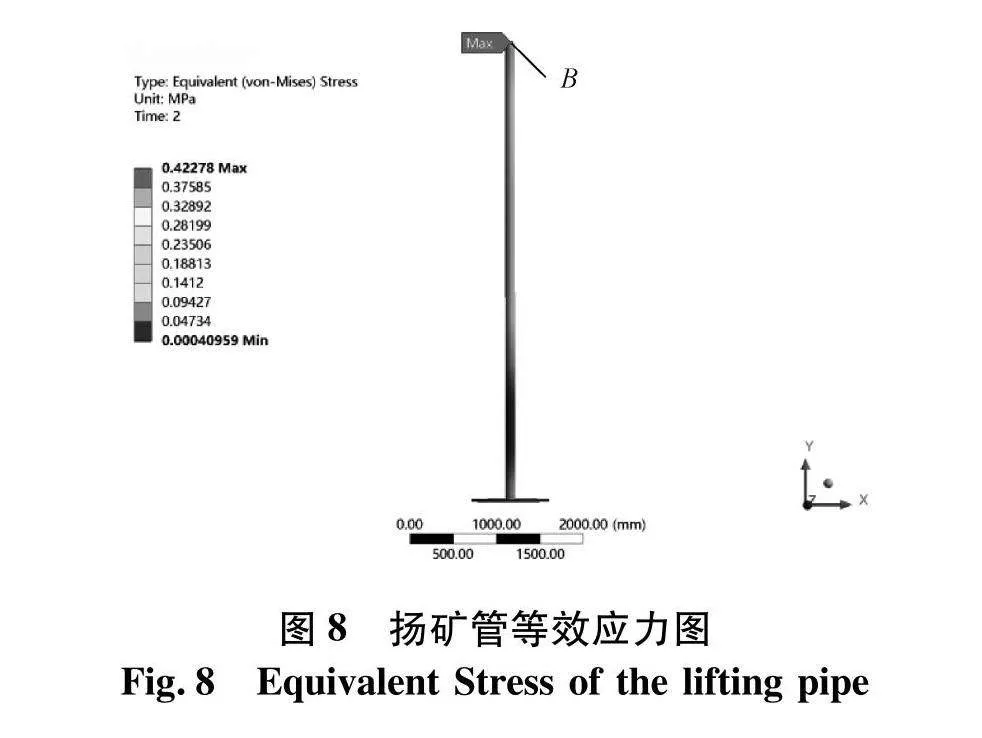
设定入口流速为2 m/s，计算所得扬矿管振动变形与等效应力云图如图7、8.

由图7可知，扬矿管的变形自上而下逐渐增加，最大值出现在距中间仓0.5 m处，为0.733 2 mm，扬矿管末端靠近中间仓位置的变形为0.697 6 mm，两者相差4.9%.从图8可以看出，扬矿管的最大应力出现在顶端连接处，其值为0.422 8 MPa，在扬矿管与中间仓的连接处也存在比较大的应力集中，这与文献［21］所得结论相一致.

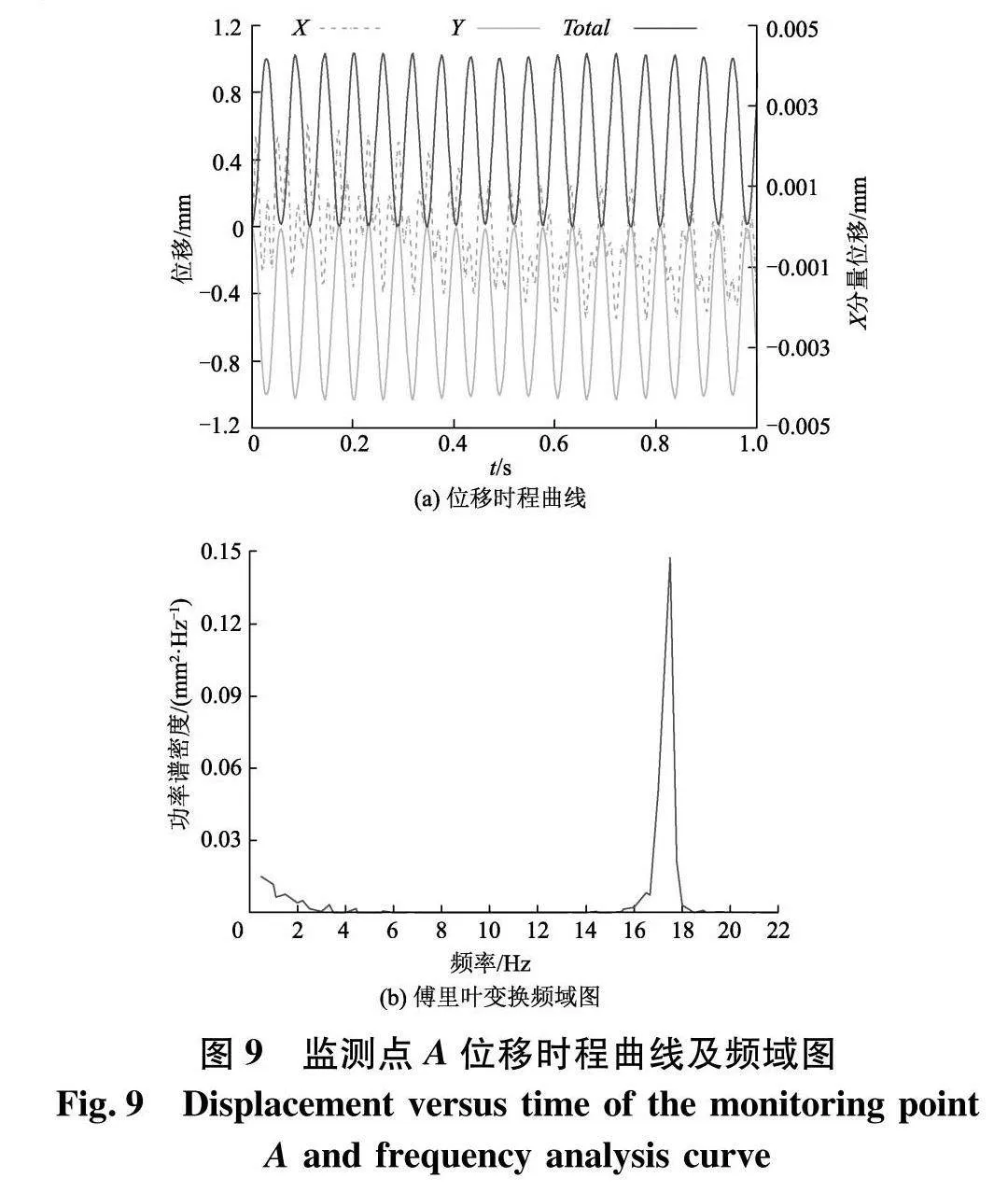
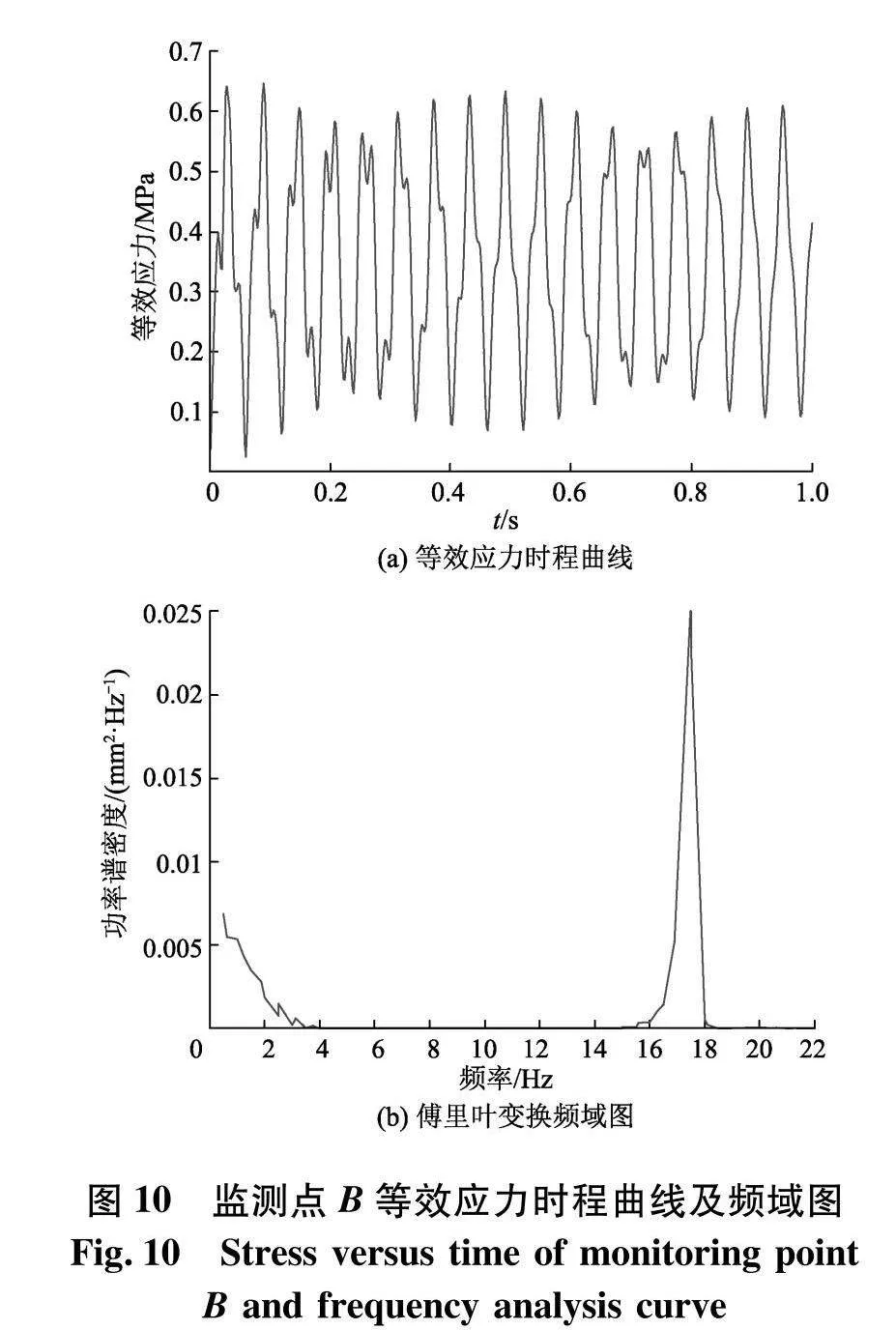
选取扬矿管最大变形处一点作为监测点A，坐标为（3.596，-4 448.534，-55.713），单位为mm.图9为监测点A在2 m/s流速下振动位移的时程曲线以及对总位移进行快速傅里叶变换（fft）所得的频域图.由于扬矿管在水平方向上的振动位移具有对称性，故仅依右侧纵轴画出A点在X方向的分位移.选取扬矿管应力集中处一点作为监测点B，坐标为（17.28，0，-53.027），单位为mm，图10为监测点B的等效应力时程曲线及相应fft频域图.

由图9、10可知，在仅考虑内流场作用下，扬矿管的振动主要表现为纵向振动，水平方向振幅约为扬矿管的纵向振幅的0.8%；恒定流速下，扬矿管主要以12阶固有频率（引起最大振幅的共振频率）在振动.

进一步计算内流流速为自2 m/s增加到12 m/s过程中扬矿管的最大振动位移与最大等效应力时程变化曲线.计算所得曲线波形与监测点A、B相一致，仅在幅值上呈现下降趋势.最大位移与最大等效应力幅值下降的原因是由于流速的增加会提升流体作用在扬矿管内壁面上的粘性阻力，进而平衡一部分采矿船对扬矿管的拉力，减轻了扬矿管顶端的应力集中，降低了扬矿管的振动位移幅值.

4.2"脉动流速对扬矿管振动的影响

由于提升泵的周期性工作以及一些其他扰动源的存在，扬矿管内的流体不会始终处于稳定状态，其速度会在一定范围内以脉动形式波动，可以视为在平均值基础上叠加脉动值.设置时间步为0.001 s，计算扬矿管在1 s内的流固耦合振动特性.通过改变入口流速的平均值、幅值、频率，记录扬矿管最大响应处的位移时程曲线.设置入口速度变化为：

Ut=U+Asin（2πft）（7）

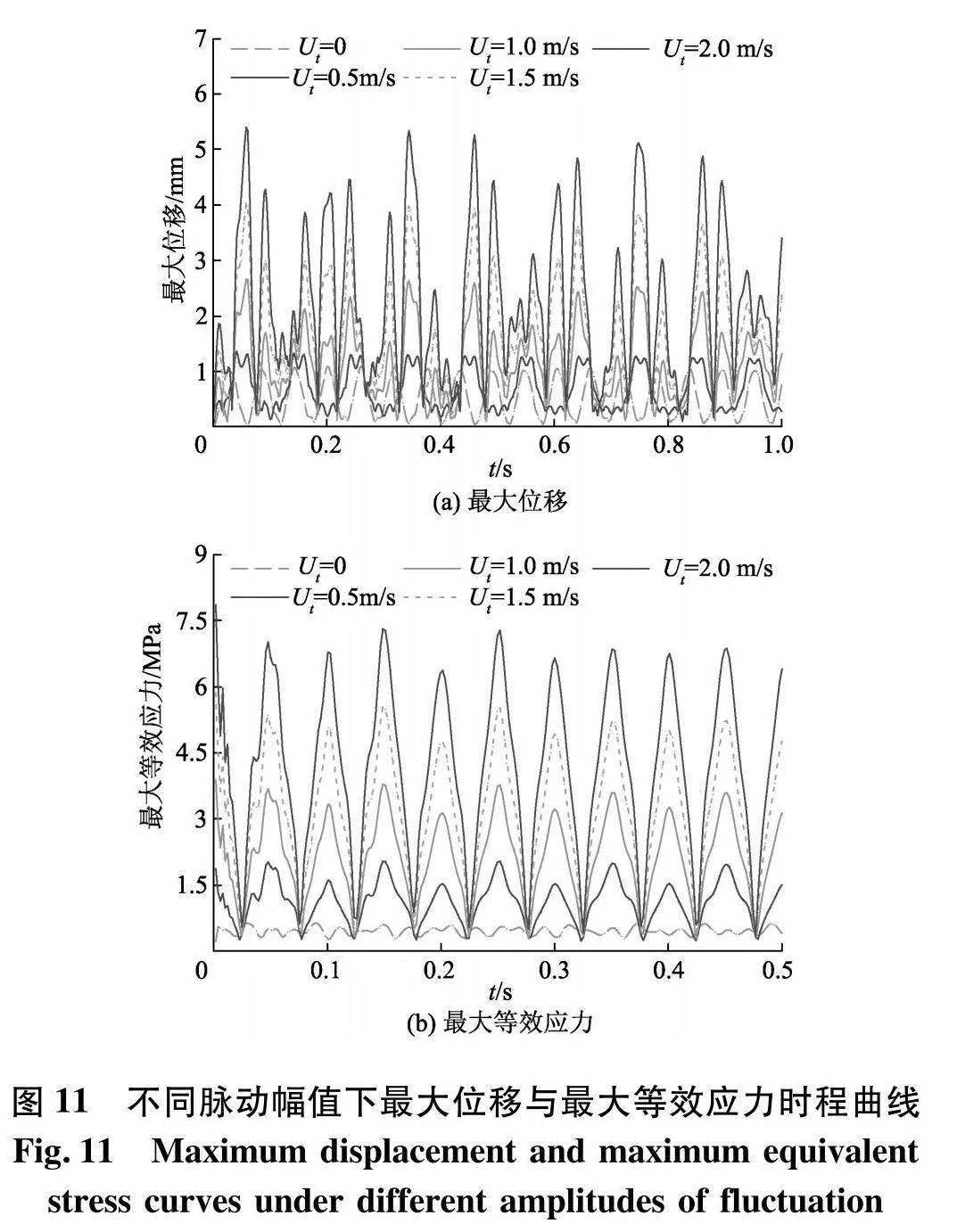
设定平均流速U为2 m/s，脉动频率f为10 Hz，改变入口流速的脉动幅值，使之从0开始以0.5 m/s的间隔逐步增加到2 m/s.管道最大位移及最大等效应力时程曲线如图11.

由图11可知，脉动内流幅值大于0.5 m/s时，扬矿管振动位移与等效应力接近线性增加.

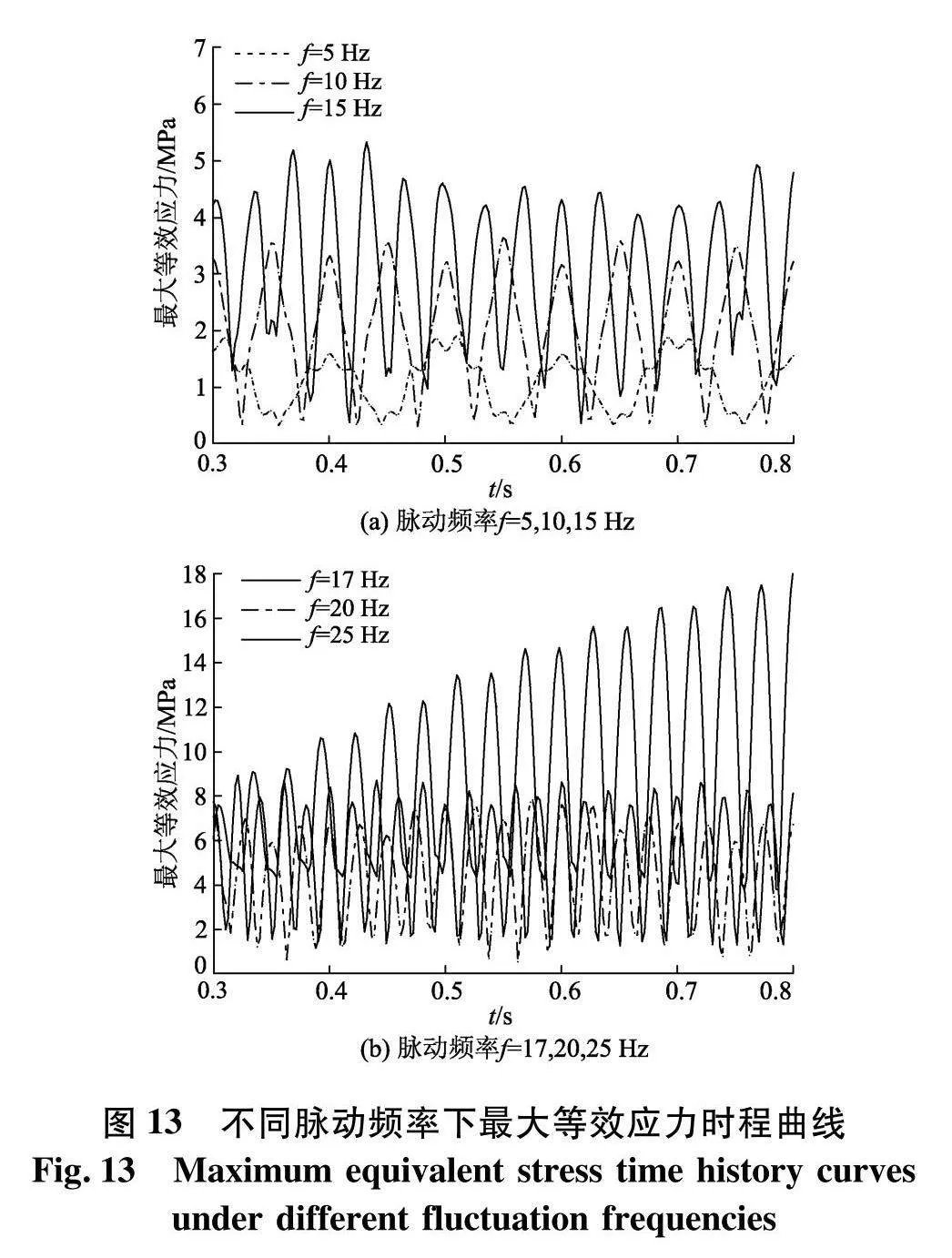
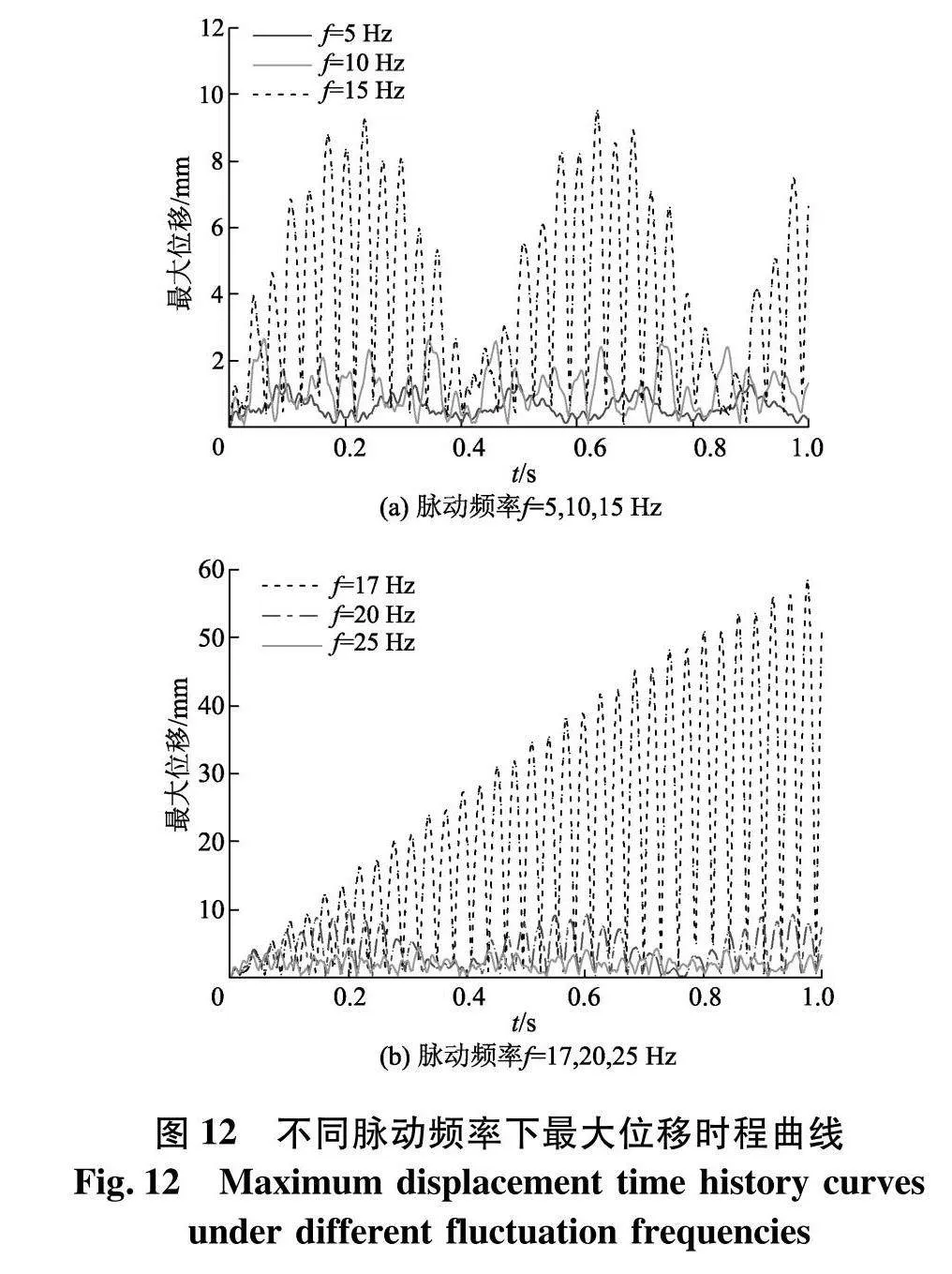
设置流体平均流速U为4 m/s，脉动幅值A为1 m/s，分别取脉动频率f为5、10、15、17、20及25 Hz，扬矿管最大位移与最大等效应力时程曲线如图12、13.结果表明，在平均流速、脉动幅值保持不变时，随着脉动频率的增加，扬矿管的振幅先增大后减小.当脉动频率取17 Hz时，扬矿管振幅随时间演变呈现发散状态，在短时间内迅速增加.综合上文谐响应分析结果，可以确定此时流体脉动频率与扬矿管12阶固有频率相接近引发了共振现象，致使扬矿管振幅严重超出安全范围，这也验证了前文谐响应分析结果的准确性.

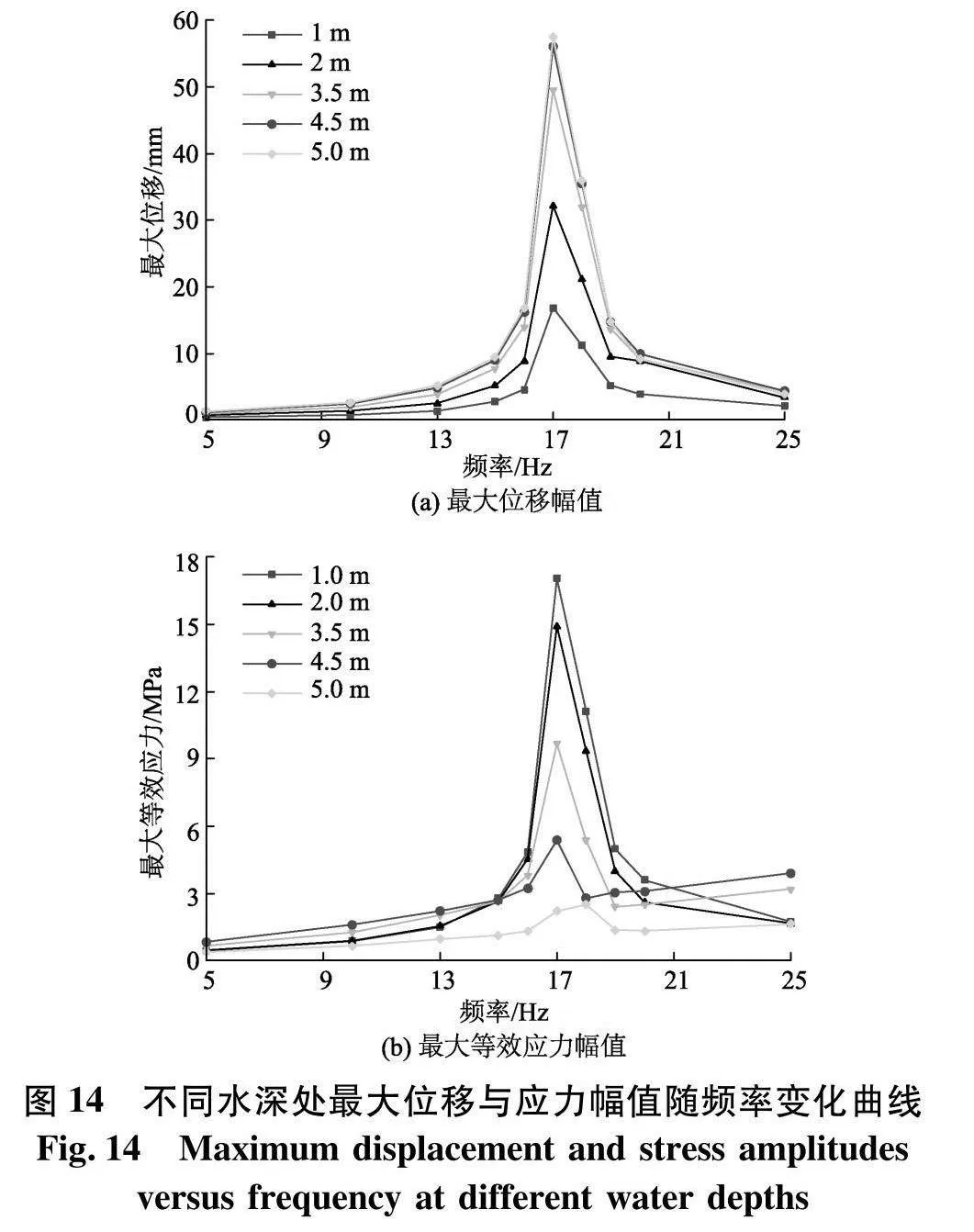
为深入分析脉动频率的改变对扬矿管在内流场作用下振动特性的影响，保持平均流速与脉动幅值不变，加密脉动频率计算间隔并在距离扬矿管顶端1、2、3.5、4.5、5 m处分别设置监测点，绘制各监测点最大位移幅值与最大等效应力幅值随内流脉动频率变化的曲线如图14.

由于脉动频率取17 Hz时，各监测点的最大位移与最大等效应力时程曲线在1 s计算时长内处于发散状态，故图14中17 Hz时的最大位移与最大等效应力幅值取靠近1 s时刻最后一个波峰的峰值.

由图14（a）可知，脉动频率从5 Hz增加到25 Hz，扬矿管不同水深处监测点的振动位移幅值先增大后减小，在脉动频率为17 Hz时达到峰值.随着水深的增加，扬矿管的振动位移幅值逐渐增加.图中4.5 m与5 m处的监测点振动位移幅值曲线接近重叠，说明在靠近中间仓约0.5 m范围内，扬矿管的振动位移幅值趋于稳定.

由图14（b）可知，扬矿管在内流场作用下产生的共振现象，会改变扬矿管等效应力的分布.脉动内流频率取5 Hz时，最大等效应力的位置出现在4.5 m水深处，1、2、5 m处等效应力幅值接近重叠；随着脉动频率的增加至17 Hz，各水深处等效应力幅值出现不同程度的增长，越靠近扬矿管的顶端，等效应力幅值增量越大，最大等效应力分布沿水深方向依次递减；随着脉动频率继续增加，各水深处最大等效应力幅值呈现衰减趋势；脉动频率增加到25 Hz，扬矿管等效应力的分布恢复到脉动频率为5 Hz时的状态.这是因为内流脉动频率越接近扬矿管的12阶固有频率，其振动的幅值就越大，导致了扬矿管顶端的应力集中.

综上可知，随着水深的增加，脉动频率变化对扬矿管振动位移的影响逐渐增大；存在以17.4 Hz为中心、跨度达8 Hz的共振带，在共振带范围内，扬矿管的等效应力变化幅值沿水深的增加逐渐减小，最大等效应力位置出现在扬矿管顶端.

4.3"结构参数对扬矿管振动的影响

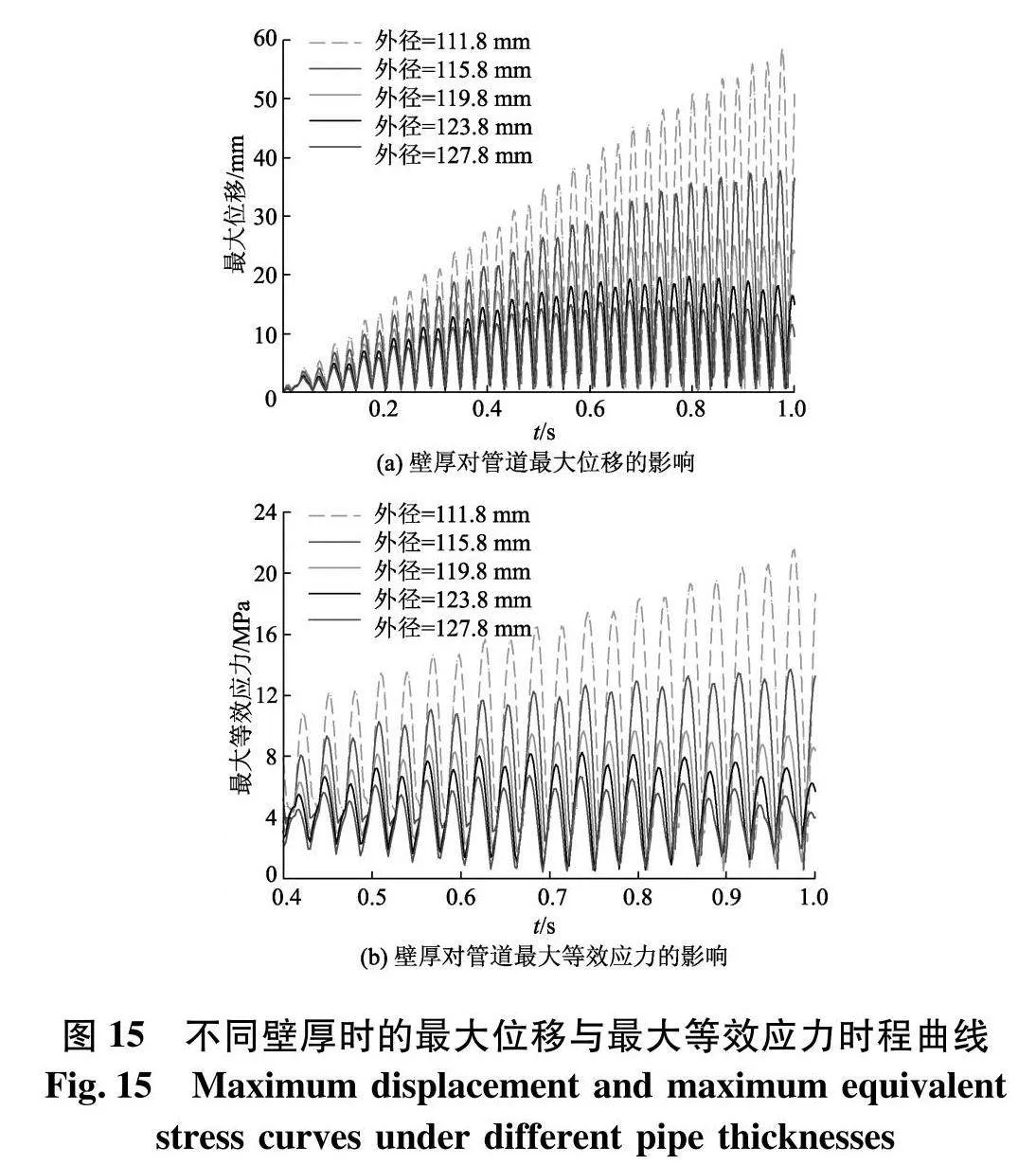
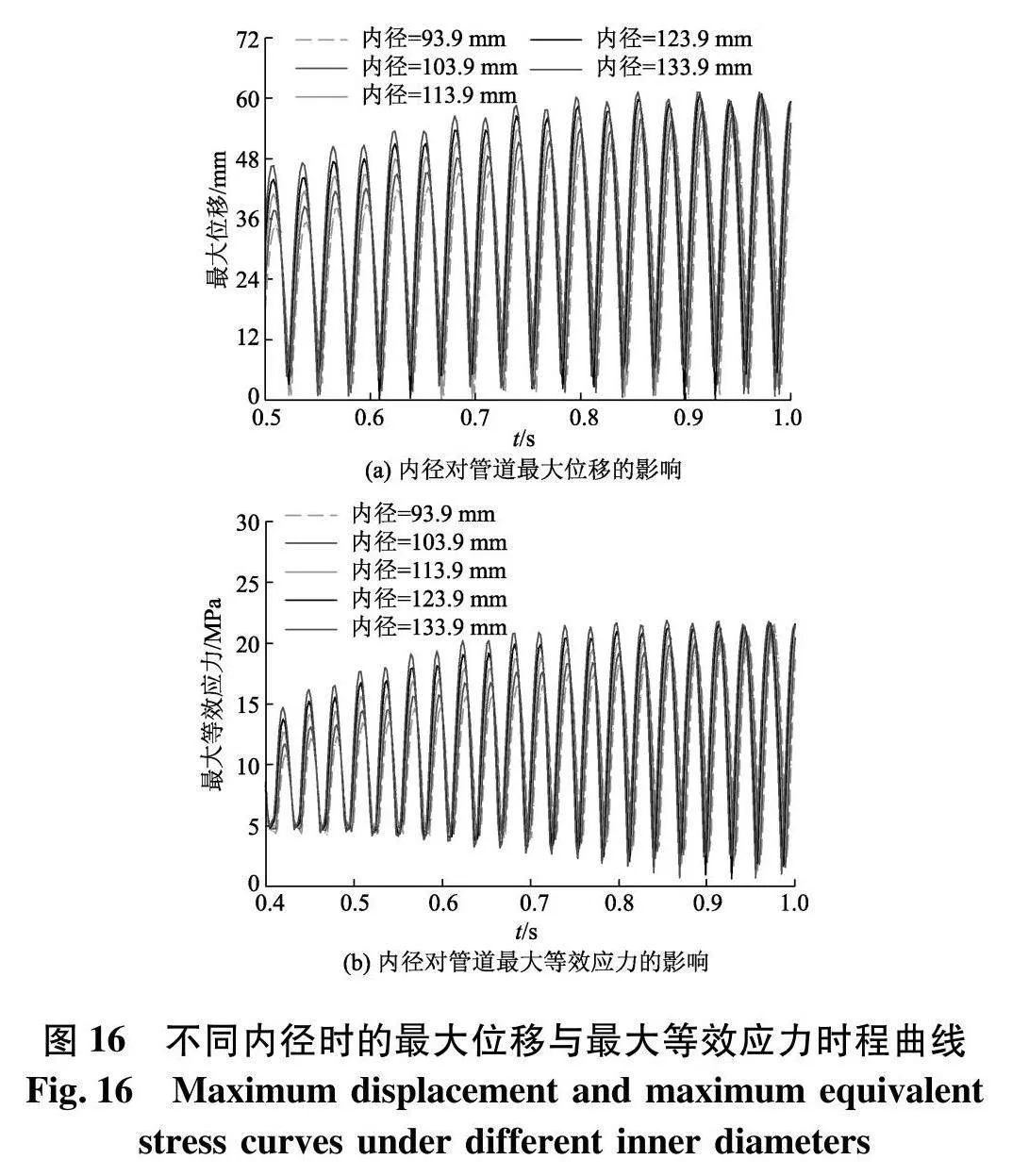
文中分析了管壁厚度、内径对扬矿管预应力模态频率的影响，为进一步探究管壁厚度、内径对扬矿管共振行为的作用效果，以接近扬矿管共振频率的内流场激励频率计算扬矿管在内流场作用下的最大位移与最大等效应力.设置内流场平均流速U为4 m/s，脉动幅值A为1 m/s，脉动频率f为17 Hz；保持内径不变，外径分别设为111.8、115.8、119.8、123.8、127.8 mm，分析壁厚对扬矿管共振行为的影响，计算结果如图15；保持壁厚不变，内径分别设为93.9、103.9、113.9、123.9、133.9 mm，分析内径对扬矿管共振行为的影响，计算结果如图16

由图15可知，内流激励频率接近扬矿管共振频率时，随着壁厚的增加，扬矿管的最大位移与最大等效应力随时间变化由发散到高位震荡再到逐渐回落；扬矿管的最大位移与最大等效应力时程曲线的幅值不断下降，且下降的趋势逐渐变缓.以0.917 5 s的数据为例，保持内径不变，当外径从111.8 mm增加到115.8 mm，最大位移下降了21.27 mm，最大等效应力下降了7.7 MPa；外径从123.8 mm增加到127.8 mm，最大位移仅下降了4.53 mm，最大等效应力仅下降了1.61 MPa；外径从111.8 mm增加到127.8 mm，壁厚增加了89%，相应的振动位移峰值由55.901 mm降低到20.53 mm，下降了63%.

由图16可知，随着内径的增加，扬矿管的最大位移与最大等效应力的发散趋势得到有效抑制，最大位移与最大等效应力的时程曲线幅值先是逐渐趋于高位震荡状态而后出现微幅回落的趋势.内径从93.9 mm增加到123.9 mm，增加了31.9%，振动位移峰值变化范围小于2.7 mm，约为振动位移峰值的4.6%.

5"结论

（1） 在仅考虑内流作用下，扬矿管振幅最大的共振频率为12阶固有频率，对应的振型为纵向振动；恒定内流流速下，扬矿管振动位移时程曲线的主要频率成分为12阶固有频率.

（2） 在距中间仓约10%管长的范围内，扬矿管的振动位移幅值保持稳定，幅值变化低于5%.

（3） 脉动内流频率与扬矿管的12阶固有频率相接近时会导致共振现象.共振现象发生后，保持壁厚不变，内径增加31.9%，扬矿管的振动位移由发散状态转变为高位震荡状态，振动峰值变化范围低于5%；保持内径不变，壁厚逐渐增加89%，扬矿管的振动位移由随发散到高位震荡再到逐渐回落，振动峰值削减了63%.壁厚的等幅调整对扬矿管共振行为的抑制作用逐渐减小.

（4） 在脉动流速下，脉动幅值大于0.5 m/s时，扬矿管的最大振动位移与等效应力幅值接近线性增加；随着内流脉动频率的增加，存在以12阶固有频率（17.443 Hz）为中心、跨度达8 Hz的共振带，在共振带范围内，扬矿管的等效应力变化幅值沿水深的增加逐渐减小，最大等效应力位置出现在扬矿管顶端.

参考文献（References）

［1］"阳宁， 陈光国. 深海矿产资源开采技术的现状综述 ［J］. 矿山机械， 2010， 38（10）： 4-9.

［2］"杨建民， 刘磊， 吕海宁，等. 我国深海矿产资源开发装备研发现状与展望［J］. 中国工程科学， 2020， 22（6）： 1-9.

［3］"沈义俊，陈敏芳，杜燕连，等.深海矿物资源开发系统关键力学问题及技术挑战［J］.力学与实践， 2022， 44（5）： 1005-1020.

［4］"WU Qi， YANG Jianmin， LU Haining， et al. Effects of heave motion on the dynamic performance of vertical transport system for deep sea mining ［J］. Applied Ocean Research， 2020， 101（7）：102188.

［5］"陈智昊， 吕海宁， 吴琪. 深海采矿系统长距离垂直输运管道力学性能研究［J］. 海洋工程， 2021， 39（1）：72-82.

［6］"李艳， 贾广成， 刘少军. 考虑流固耦合的深海采矿长输流硬管力学行为［J］. 中南大学学报（自然科学版）， 2016， 47（11）：3670-3676.

［7］"李艳， 廖科伏， 卢飞，等. 考虑流固耦合的1000m深海扬矿硬管动力学分析［J］. 水资源与水工程学报， 2017， 28（1）： 163-168.

［8］"VIERENDEELS J， LANOYE L， DEGROOTE J， et al. Implicit coupling of partitioned fluid-structure interaction problems with reduced order models ［J］. Computers and Structures， 2007， 85 （11/12/13/14） ： 970-976.

［9］"HUANG Yimin， LIU Yongshou， LI Baohui， et al. Natural frcqucncy analysis of fluid convcying pipcline with diffierent conditions［J］. Nuclear Engineering and Design， 2010，240（3）：461-471.

［10］"KTTLER U， WALL W. Fixed-point fluid-structure interaction solvers with dynamic relaxation ［J］. Computational Mechanics， 2008，43 （1） ： 61-72.

［11］"LIU Jun， ZHAO Hongliang， LIU Qingyou， et al. Dynamic behavior of a deepwater hard suspension riser under emergency evacuation conditions［J］. Ocean Engineering， 2018， 150： 138-151.

［12］"MA Yongqi， YOU Yunxiang， CHEN Ke， et al. Application of harmonic differential quadrature （HDQ） method for vibration analysis of pipes conveying fluid［J］. Applied Mathematics and Computation， 2023，439：127613.

［13］"DUAN Jinlong， ZHOU Jifu， YOU Yunxiang， et al. Time-domain analysis of vortex-induced vibration of a flexible mining riser transporting flow with various velocities and densities［J］. Ocean Engineering， 2021， 220： 108427.

［14］"DUAN Jinlong， ZHOU Jifu， YOU Yunxiang， et al. Effect of internal flow on vortex-induced vibration dynamics of a flexible mining riser in external shear current［J］. Marine Structures， 2021， 80： 103094.

［15］"阳宁， 周知进， 唐达生，等. 粗颗粒水下管道输送系统振动的实验研究［J］. 海洋工程， 2014， 32（3）：104-109.

［16］"唐达生， 李钟， 周知进，等. 锰结核泵工作对扬矿管道振动影响的研究［J］. 振动与冲击， 2015， 34（23）：149-152，160.

［17］"宋庆辉， 肖林京， 姜海燕，等. 基于ABAQUS的深海采矿扬矿管纵向振动性能［J］. 西南交通大学学报， 2022（4）：57.

［18］"刘辉， 邓旭辉， 赵珂，等. 不同约束条件对深海采矿输送管道动力学的影响［J］. 应用力学学报， 2022（3）： 506-515.

［19］"徐海良，龙国键， 梁武. 深海采矿矿石输送软管的力学实验分析［J］.矿业研究与开发， 2006， 26（1）：47-50.

［20］"古磊， 陈科， 盛立， 等. 高雷诺数圆湍潜射流的数值模拟研究［J］. 江苏科技大学学报（自然科学版）， 2021， 35（4）：1-8.

［21］"刘金书， 禹宏云， 马慧坤. 6 000 m深海扬矿系统仿真分析［J］. 计算机仿真， 2009（7）：333-336.

（责任编辑：贡洪殿）