基于哈希桶和聚类的变半径邻域粗糙集模型

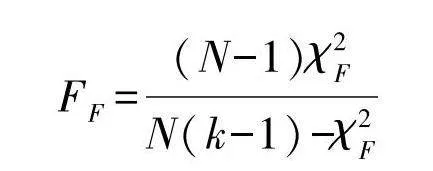
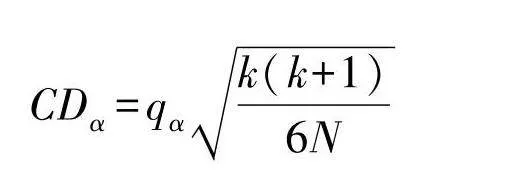
摘"要： 邻域粗糙集是处理机器学习与数据挖掘中不确定性的数据分析工具．邻域粗糙集中邻域粒的大小往往受邻域半径的影响．针对现有的邻域粗糙集模型通常对每个样本设置相同的邻域半径，导致得到的邻域粒无法对每个样本进行准确地刻画的问题，基于样本数据的分布信息，首先对数据集进行聚类，并基于哈希桶对每个类的样本分布情况做出分析，然后为每个样本设置合适大小的邻域半径，使其能够更准确地刻画每个样本的信息，进而提出变半径邻域粗糙集模型．最后选取了8个UCI数据集进行实验，并分别与当前最常用的邻域粗糙集模型进行比较，理论分析与实验结果表明所提出的变半径邻域粗糙集模型具有更好的学习性能．

关键词： 变半径邻域粗糙集；哈希桶；聚类；样本分布；不确定性

中图分类号：TP301"""文献标志码：A"""""文章编号：1673-4807（2024）04-100-08

Variable radius neighborhood rough set model based onhash bucket and clustering

LI Hua， MENG Xiangrui

（Department of Mathematics amp; Physics，Shijiazhuang Tiedao University， Shijiazhuang 050043，China）

Abstract：Neighborhood rough set is a data analysis tool that handles uncertainty in machine learning and data mining. The size of neighborhood granules in neighborhood rough set models is often affected by neighborhood radius. However， existing neighborhood rough set models usually do not consider the distribution information of sample data， and set the same neighborhood radius for each sample， resulting in the neighborhood granules being unable to accurately depict each sample. To address this problem， based on the distribution information of data， a variable radius neighborhood rough set model is proposed. Firstly， the dataset is clustered， and the sample distribution of each class is analyzed based on the hash bucket， and then the appropriate neighborhood radius is set for each sample， so that the information of each sample can be more accurately described. Finally， on eight data sets， the variable radius neighborhood rough set model is compared with popular neighborhood rough set models. Theoretical analysis and experimental results show that the variable radius neighborhood rough set model proposed in this paper has better learning performance.

Key words：variable neighborhood rough sets， hash bucket， clustering， sample distribution，uncertainty

粗糙集理论［1］是一种描述数据不完整性与不确定性的数学工具，能够定量分析不精确、不一致和不完整等各种不完备的信息．由于经典粗糙集理论无法直接应用于连续型数据集，文献［2］提出了邻域粗糙集理论（neighborhood rough set，NRS）．这种模型使用距离定义样本间的相似性，将等价关系泛化为邻域关系，使粗糙集理论的应用范围拓宽到了连续型数据．目前邻域粗糙集理论已被广泛应用于信息安全、图像处理及决策分析等领域．

邻域粗糙集通过设置邻域半径来确定样本的邻域粒，合适的邻域半径对于构建邻域粗糙集模型至关重要．许多学者对邻域半径展开了研究．文献［3］提出使用数据集中每一列条件属性值的标准差所构成的阈值向量作为邻域半径．这种方法只能选择曼哈顿距离作为距离度量，一定程度上限制了邻域的构造方式．文献［4］基于标准差的阈值向量设定统一的单邻域半径，增大了距离度量的选择范围．以上方法未考虑数据集样本空间的分布，为数据集设定了同一个邻域半径．统一的邻域半径并不能准确地描述数据集中的所有样本．因此，许多学者为数据集设定了多个邻域半径．文献［5］提出k最近邻邻域粗糙集模型，将k近邻粗糙集模型与邻域粗糙集模型相结合，固定每个邻域中样本个数从而对不同样本的分布情况进行区分．文献［6］提出无需设定参数的邻域关系Gap，根据样本之间的距离远近划分邻域范围，使得新邻域包含样本个数更少．文献［7］依据邻域中包含样本类别数目重新设定邻域半径，包含样本类别个数与半径大小呈负相关．以上方法基于局部的样本分布信息构造新的邻域半径，欠缺考虑数据集总体样本分布，所构造的邻域半径并非完全适合于每个样本．

文中对比分析数据集中样本的总体分布与局部分布情况，为每个样本设定合适的邻域半径，提出了变半径邻域粗糙集模型．首先通过计算数据集条件属性值的标准差得到依据总体分布的统一邻域半径，同时使用数据集中非空哈希桶刻画样本总体分布情况，然后将样本聚类，用类内哈希桶包含样本的平均个数刻画各个类的样本分布情况．最后根据类内分布情况与总体分布情况的对比得到每个类的邻域半径，进而给出变半径邻域粗糙集模型的定义．通过理论证明了变半径邻域粗糙集模型具有更高的分类精度与近似质量，同时在UCI数据集上的实验结果表明变半径邻域粗糙集模型具有更好的学习性能．

1"基本概念

1.1"邻域粗糙集

设S=（U，C，D，V，f）是一个决策信息系统，其中U={x1，x2，…，xn}为非空样本集合；C为样本的条件属性集合；D为样本的决策属性集合；V为所有属性的值域，Vi为属性ai的值域； f：U×C∪D→V表示信息函数．即对任意ai∈C∪D，x∈U，均有fi（x）∈Vi．决策信息系统也称为决策表［2］，可简化表示为S=（U，C，D）．

下面给出邻域的定义．

定义1［2］ 设S=（U，C，D）为决策信息系统，条件属性集合BC，给定任意x∈U，x的邻域RB（x）定义为：

RB（x）={yy∈U，ΔB（x，y）≤r}

式中：ΔB：U×U→R+为样本在属性子集B的距离函数．常用的距离函数有欧氏距离、曼哈顿距离和切比雪夫距离等．r为邻域半径，通常为常数，用于确定样本的邻域大小．

根据条件属性集合给出样本的邻域后，可用两个精确集，即上、下近似刻画任意集合X，由此得到邻域粗糙集模型的定义．

定义2［2］ 设S=（U，C，D）为决策信息系统，条件属性集合BC．设集合XU，X关于属性集B的上、下近似分别定义为：

NBX={xRB（x）∩X≠，x∈U}

NBX={xRB（x）X，x∈U}

上、下近似可用于逼近任意集合X，同时上、下近似构成的模型称为邻域粗糙集模型．特别地，若X为决策，可得到决策D关于B的上、下近似．

定义3［2］ 设S=（U，C，D）为决策信息系统，条件属性集合BC．决策属性集D将U划分为s个等价类，即决策类D1，D2，…，Ds，决策D关于属性集B的上、下近似为：

NBD=∪si=1NBDi

NBD=∪si=1NBDi

式中：NBDi、NBDi分别为决策类Di关于属性集B的上、下近似．

给出邻域粗糙集模型中分类能力与近似能力的度量．

定义4［8］ 设S=（U，C，D）为决策信息系统，条件属性集合BC．决策D关于B的上、下近似分别为NBD、NBD，则决策D关于属性集B的分类精度为：

PB（D）=NBDNBD

定义5［8］ 设S=（U，C，D）为决策信息系统，条件属性集合BC．决策D关于B的下近似为NBD，则决策D关于属性集B的近似质量为：

QB（D）=NBDU

分类精度指出了所有可能的决策中正确决策所占的比例，近似质量表明了基于知识B可以准确做出决策的对象的比例．

1.2"哈希桶

文献［9］以邻域半径为间距将数据集划分为一系列桶，提出哈希桶的概念，并应用哈希桶缩小邻域的搜索范围．哈希桶的具体定义如下：

定义6"设S=（U，C，D）为决策信息系统，C={a1，a2，…，am}为条件属性集，哈希桶Hk为：

Hk={xx∈U∧［ΔC（x0，x）/r］=k}

式中：［y］表示对y向下取整；ΔC为样本在条件属性集C上的距离函数；r为预先设定的邻域半径；k为非负整数；x0是由样本在各个条件属性上的最小取值所构成的向量．

哈希桶中样本个数反映了桶内样本的疏密程度．桶中样本个数越多，样本分布越密集，反之，样本分布越稀疏．因此，样本的局部分布情况可用其所在哈希桶中样本的个数刻画．

2"变半径邻域粗糙集模型

已有邻域粗糙集模型在构造邻域半径时未考虑总体样本分布，所构造的邻域半径并非完全适合于每个样本．因此，结合样本总体分布与局部分布信息构造适合每个样本的邻域半径．首先给出适合总体样本分布的统一半径，并通过数据集中哈希桶平均包含样本个数刻画数据集总体样本分布，然后通过聚类区分处于不同分布的样本，再使用类内哈希桶刻画各个类的样本分布情况．最后根据类内分布情况与总体分布情况的对比得到每个类的邻域半径，进而得到变半径邻域粗糙集模型．

首先，给出适合总体样本分布的邻域半径，即使用条件属性的标准差作为数据集的统一半径．

定义7［4］ 设S=（U，C，D）为决策信息系统，U={x1，x2，…，xn}，C={a1，a2，…，am}，统一半径δ定义为：

δ=std{δ（a1），δ（a2），…，δ（am）}

式中：

δ（ai）=1λstd{fi（x1），fi（x2），…，fi（xn）} i=1，…，m；

std{x1，x2，…，xn}为变量x1，x2，…，xn的标准差；fi（x）为样本x在属性ai下的取值；λ为依据数据集而定的特征参数．进一步，通过哈希桶刻画数据集的总体分布情况．

定义8"设S=（U，C，D）为决策信息系统，哈希桶H0，H1，H2，…，Hp．数据集U的总体分布率D（H）为：

D（H）=∪0≤k≤pHkq=Uq

式中：q为数据集中非空哈希桶的个数．

数据集U的总体分布率D（H）为数据集中所有非空哈希桶包含样本数的平均值，其反映了数据集中样本的总体分布情况．由定义可知D（H）≥1．

为了准确刻画数据集中处于不同分布的样本，首先对数据集进行聚类．同一类中的样本相似度较高，不同类的样本相似度较低．因此处于同一类中的样本具有相同的分布情况．使用k-means聚类方法将数据集U划分为w个类，即E1，E2，…，Ew，这里w依据文献［10］确定．

定义9"设S=（U，C，D）为决策信息系统，哈希桶为H0，H1，H2，…，Hp，其中非空哈希桶为Hq1，Hq2，…，Hqt（1≤qt≤p）．给定聚类E1，E2，…，Ew，类Ei（i=1，…，w）的类内哈希桶为：

H（Ei）=∪q1≤j≤qt{Hj|Hj∩Ei≠}"HjEi

∪q1≤j≤qt{Hj|HjEi}"否则

如果类Ei包含若干个哈希桶，则H（Ei）由完全包含在类内的非空哈希桶构成，如果类Ei不包含任何非空哈希桶，则H（Ei）由所有与Ei相交非空的哈希桶构成．

用类内哈希桶包含样本的个数刻画每个类的样本分布情况．

定义10"设S=（U，C，D）为决策信息系统，哈希桶为H0，H1，H2，…，Hp．给定聚类E1，E2，…，Ew，类Ei（i=1，…，w）的分布率Pi为：

Pi=H（Ei）t

式中：t为类Ei的类内哈希桶H（Ei）中所包含哈希桶的个数．类Ei的分布率Pi为该类中每个哈希桶包含样本数的平均值．由定义9可知，构成H（Ei）的每个桶至少包含一个样本，因此Pi≥1．Pi越大，表明类Ei中样本分布越密集，反之样本分布越稀疏．因此Pi刻画了类Ei中样本的分布情况．

通过对比类内样本分布与总体样本分布来刻画类内样本的疏密程度．

定义11"设S=（U，C，D）为决策信息系统，哈希桶为H0，H1，H2，…，Hp．给定聚类E1，E2，…，Ew，类Ei（i=1，…，w）对数据集U的相对比Mi为：

Mi=PiD（H）

类Ei对数据集U的相对比Mi是类内分布率与总体分布率之比．由定义可知，Migt;0．Mi越大，表明类Ei中样本分布相对密集，反之则表明类Ei中样本分布相对稀疏．对于分布较为密集的样本，邻域半径应小于基于总体样本分布的统一半径．对于分布较为稀疏的样本，为使样本的邻域粒能够更为细致地刻画样本信息，这里仍采用统一半径．因此，基于相对比Mi，通过调整数据集的统一半径来计算类Ei的类半径．

定义12"设S=（U，C，D）为决策信息系统，统一半径为δ，哈希桶为H0，H1，H2，…，Hp．给定聚类E1，E2，…，Ew，类Ei（i=1，…，w）对数据集U的相对比为Mi，则类Ei的类半径为：

δ（Ei）=ε1Miδ"1lt;Mi

δ0lt;Mi≤1

式中：ε为调节参数，一般0lt;ε≤1．

变半径邻域可根据相应类半径定义．

定义13"设S=（U，C，D）为决策信息系统，条件属性集合BC，给定聚类E1，E2，…，Ew，类Ei（i=1，…，w）的类半径为δ（Ei）．设x∈Ei，则x的变半径邻域δB（x）为：

δB（x）={yy∈U，ΔB（x，y）≤δ（Ei）}

式中：ΔB：U×U→R+为样本在属性集B的距离函数．

根据条件属性集合给出样本的变半径邻域后，可用两个精确集刻画任意集合X，即上、下近似．由此得到变半径邻域粗糙集模型的定义．

定义14"设S=（U，C，D）为决策信息系统，条件属性集合BC．设XU，X在变半径邻域粗糙集中关于属性集B的上、下近似分别定义为：

KBX={xδB（x）∩X≠，x∈U}

KBX={xδB（x）X，x∈U}

上、下近似可用于逼近任意集合X，同时上、下近似构成的模型称为变半径邻域粗糙集模型．

若X为决策，根据定义14可得到决策D关于B的上、下近似．

定义15"设S=（U，C，D）为决策信息系统，条件属性集合BC．决策属性集D将U划分为s个等价类，即决策类D1，D2，…，Ds．决策D在变半径邻域粗糙集中关于属性集B的上、下近似为：

KBD=∪si=1KBDi

KBD=∪si=1KBDi

式中：KBDi、KBDi分别为决策类Di在变半径邻域粗糙集中关于属性集B的上、下近似．

下面给出判别变半径邻域粗糙集模型中分类能力与近似能力的度量．

定义16"设S=（U，C，D）为决策信息系统，条件属性集合BC．决策D在变半径邻域粗糙集中关于属性集B的上、下近似分别为KBD、KBD，则变半径邻域粗糙集中决策D关于属性集B的分类精度为：

PEB（D）=KBDKBD

定义17"设S=（U，C，D）为决策信息系统，条件属性集合BC．决策D在变半径邻域粗糙集中关于属性集B的下近似为KBD，则变半径邻域粗糙集中决策D关于属性集B的近似质量为：

QEB（D）=KBDU

以下定理表明了变半径邻域粗糙集模型具有更高的分类精度与近似质量．

定理1"设S=（U，C，D）为决策信息系统，条件属性集合BC，设PB（D）与QB（D）分别为经典邻域粗糙集中决策D关于属性集B的分类精度与近似质量．PEB（D）与QEB（D）分别为变半径邻域粗糙集中决策D关于属性集B的分类精度与近似质量．则有：

PB（D）≤PEB（D）

QB（D）≤QEB（D）

证明：设S=（U，C，D）为决策信息系统，条件属性集合BC．决策D将U划分为D1，D2，…，Ds等s个决策类．设经典邻域粗糙集的邻域半径为定义7所设定的统一半径δ．RB（x）表示U中任意样本x的经典邻域．在变半径邻域粗糙集中，将U按k-means聚类方法划分为E1，E2，…，Eww个类．对于任意样本x∈E，设类E的类半径为δ（E），由定义12可知，δ（E）≤δ．设δB（x）表示x的变半径邻域．由定义13可知，δB（x）={yy∈U，ΔB（x，y）≤δ（E）}．对于任意y∈δB（x），则ΔB（x，y）≤δ（E）．由δ（E）≤δ可知ΔB（x，y）≤δ，从而y∈RB（x）．因此，δB（x）RB（x）．

设变半径邻域粗糙集中决策类Di（i=1，…，s）关于属性集B的上、下近似分别为KBDi、KBDi．经典邻域粗糙集中决策类Di关于属性集B的上、下近似分别为NBDi、NBDi．根据其定义有NBDiKBDi，KBDiNBDi．根据定义3与定义15可知， NBDKBD，KBDNBD，NBD≤KBD，KBD≤NBD．根据变半径邻域粗糙集与经典邻域粗糙集中决策D关于属性集B的分类精度与近似质量的定义，有：

PB（D）=NBDNBD≤KBDKBD=PEB（D）

QB（D）=NBDU≤KBDU=QEB（D）

定理1表明了变半径邻域粗糙集的分类精度与近似质量均高于经典邻域粗糙集．

算法1给出了变半径邻域粗糙集模型的具体计算过程.

算法1"变半径邻域粗糙集模型（neighborhood rough set model based on hash bucket and clustering，HCNRS）

输入：决策信息系统S=（U，C，D），条件属性集合BC，任意集合XU，特征参数λ

输出：变半径邻域粗糙集模型KBX、KBX

① 根据定义7，定义8计算哈希桶H0，H1，H2，…，Hp与总体分布率D（H）

② 使用k-means聚类方法将数据集U划分为w个类，即E1，E2，…，Ew；

③ 根据定义10计算各个类的分布率：P1，P2，…，Pw；

④ 根据定义12计算各个类的类半径：δ（E1），δ（E2），…，δ（Ew）；

⑤ for i=1：w

⑥ ""for k=0：p

⑦ if x∈Hk∧x∈Ei

⑧ """""初始化δB（x）=；

⑨ """"for每个y∈Hk及其相邻哈希桶

⑩ """""""if ΔB（x，y）≤δB（Ei）

δB（x）←y；/*计算样本x的邻域*/

下面分析变半径邻域粗糙集模型计算过程的时间复杂度．其复杂度主要由步骤②～④，⑤～B16的时间复杂度组成．步骤②～④为计算样本的类半径，时间复杂度为O（|U|）．步骤⑤～B16为计算样本的变半径邻域，时间复杂度为O（|U|2）．因此算法1的时间复杂度为O（|U|2）．

3"实验

3.1"实验分析

将变半径邻域粗糙集模型（HCNRS）与经典邻域粗糙集模型［3］（NRS）、变邻域粗糙集模型［7］（variable radius neighborhood rough sets，VRNRs）以及k最近邻粗糙集模型［5］（k-nearest neighborhood rough sets，NNRS）在分类精度与近似质量上进行对比实验．从UCI机器学习数据库中选择了8个数据集，数据集的具体信息如表1．使用十折交叉验证对各个模型进行实验比较，算法使用MATLAB 2017a进行编程，实验运行的硬件环境为intel（R） Core（TM） i5-7200U CPU和64 GB．

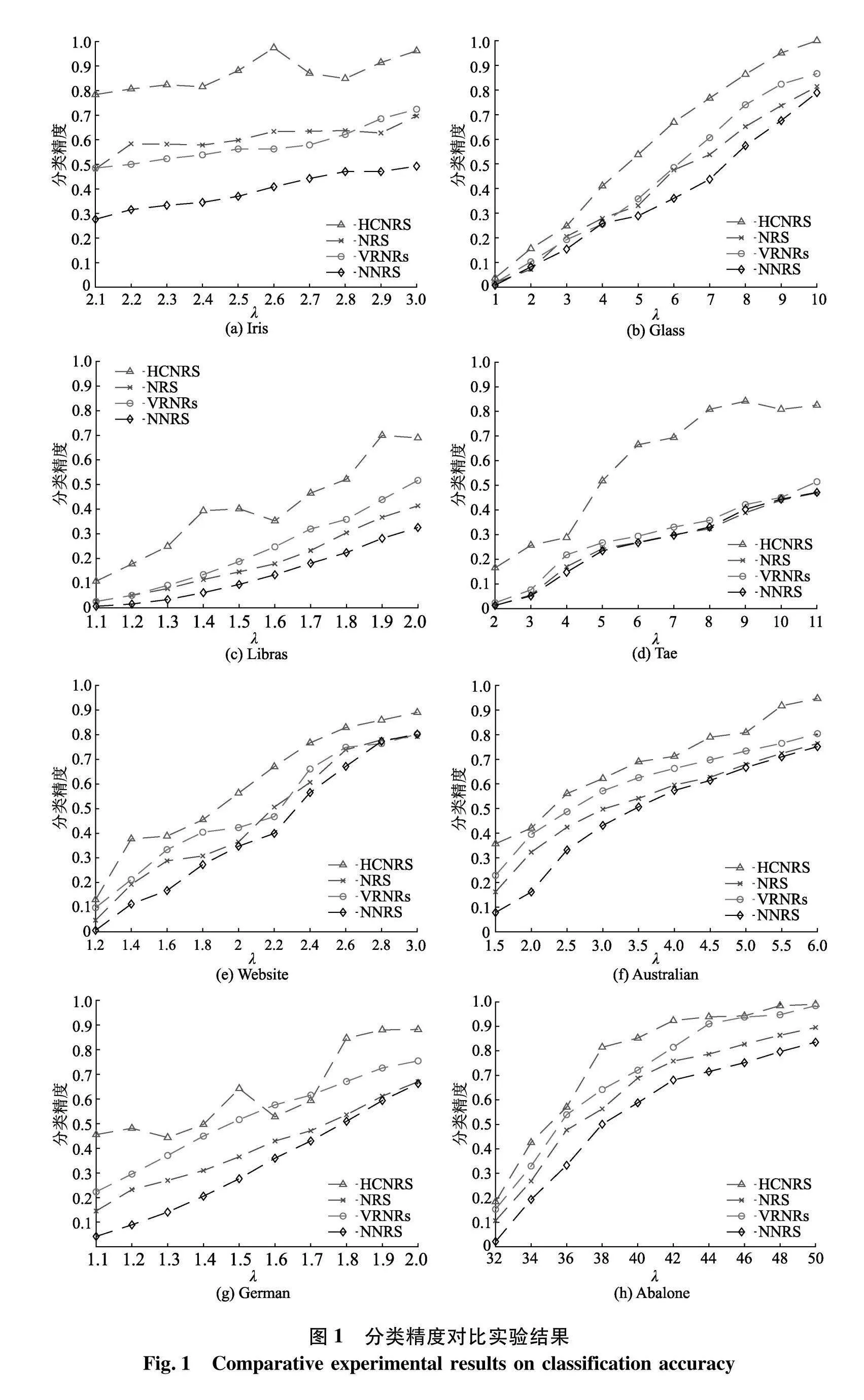
为探究随着邻域半径的改变，HCNRS与NRS、VRNRs以及NNRS在分类精度与近似质量上的变化，选择4类邻域粗糙集模型在构造邻域半径时需要设置的参数λ，并探讨随着λ的改变，变半径邻域粗糙集模型与其他3类邻域粗糙集模型在分类精度和近似质量上的变化趋势．对表1中每个数据集分别选取了10个合适大小的λ值，并分别计算各个邻域粗糙集模型在每个λ值下的分类精度值与近似质量值，结果如图1、2．

图1、图2分别展示了4类邻域粗糙集模型在8个数据集上的分类精度与近似质量随参数λ的变化趋势．在Iris、Libras、Tae和German数据集中，HCNRS的分类精度与近似质量并不随着λ的增大而单调递增．这是由于每次实验时k均值聚类的结果不同，从而影响类内哈希桶的构成，进一步地对模型的上、下近似产生一定影响．因此，随着λ的增大，分类精度与近似质量的值可能有所波动．在Iris、Glass、Libras、Tae、Australian、Website和Abalone数据集中，HCNRS的分类精度值与近似质量值始终高于其他3类邻域粗糙集模型．在German数据集中，当λ取合适的值时，HCNRS的分类精度值与近似质量值仍处于最高水平．以上对比验证了在不同的邻域半径下，变半径邻域粗糙集模型在分类精度与近似质量上的优越性．

3.2"统计实验分析

为进一步探究HCNRS与NRS、VRNRs、NNRS在分类精度与近似质量上的差异是否具有显著性，使用 Friedman 检验［11］和 Bonferroni-Dunn检验［12］对4类邻域粗糙集模型进行对比分析．

Friedman检验主要用于对多个模型进行统计比较．Ri表示第i个模型在所有数据集中关于模型性能的平均排名，Friedman检验统计量描述如下：

FF=（N－1）χ2FN（k－1）－χ2F

FF为服从自由度k－1与（k－1）（N－1）的F分布，文中N=8，k=4，显著性水平设置为0.05．

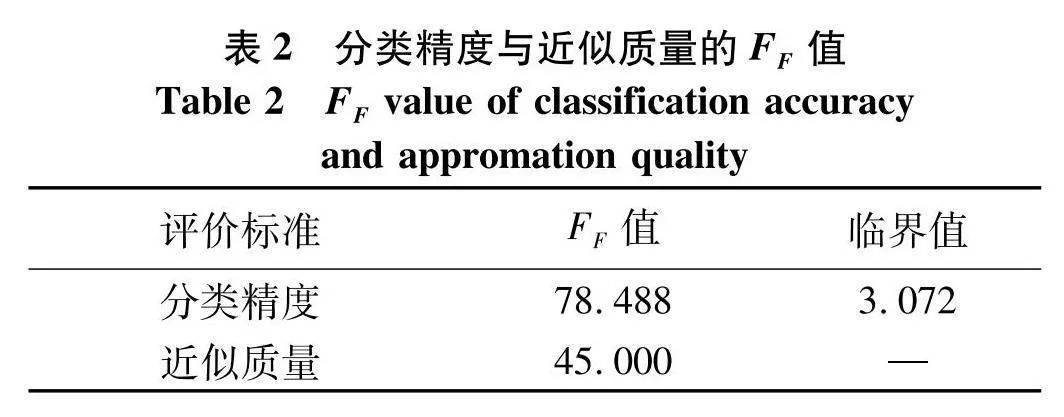
表2展示了在分类精度与近似质量下的FF值以及显著性水平为0.05的临界值．观察表2可知，分类精度与近似质量的FF值均大于临界值3.072．因此，应明确拒绝比较模型之间“相等”性能的原假设，并需要进行进一步实验区分各个邻域粗糙集模型的分类能力与近似能力．

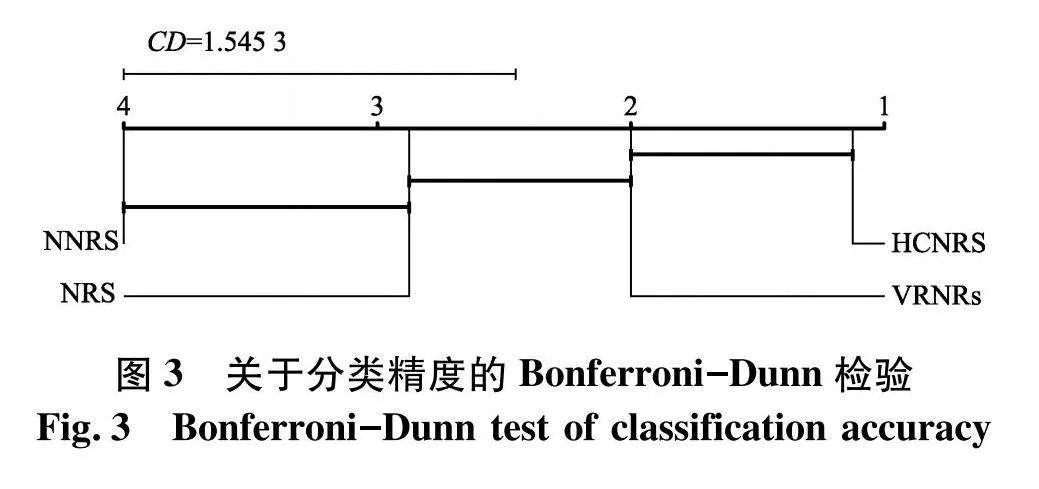
使用Bonferroni-Dunn检验区分邻域粗糙集模型之间存在明显差异．Bonferroni-Dunn检验的临界距离为：

CDα=qαk（k+1）6N

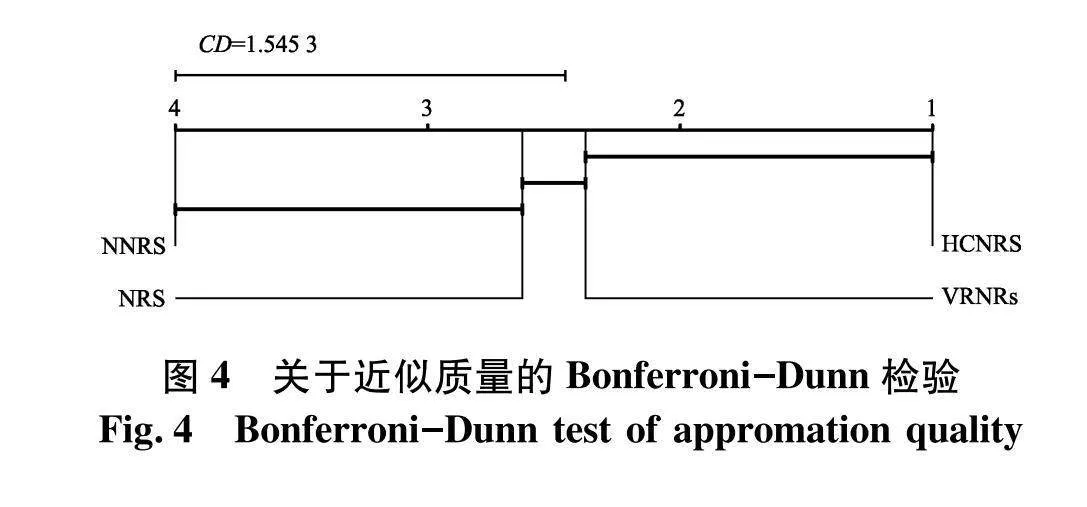
式中：k为模型的个数；N为数据集个数；qα为临界表值；α表示显著性水平，设为0.05．文中N=8，k=4． Bonferroni-Dunn检验结果如图3、4．观察图3、4可知，HCNRS在两个度量中平均排名最高，优于模型VRNRs，且明显优于模型NRS与NNRS.

4"结论

随着邻域粗糙集模型的广泛应用，邻域半径作为构造邻域粗糙集模型的关键也受到了关注．而已有邻域粗糙集模型所构造的邻域半径并非完全适合于每个样本．因此，提出一种基于哈希桶与聚类的变半径邻域粗糙集模型，该模型基于数据集局部样本分布与总体样本分布的对比为每个样本设置合适的邻域半径，生成分类性能更好的变半径邻域粗糙集模型．通过理论证明了变半径邻域粗糙集模型具有更高的分类精度与近似质量．UCI数据集上的实验结果表明变半径邻域粗糙集模型具有更好的学习性能．

文中对数据集样本进行分类时使用的k-means聚类方法具有随机性，在多次实验中，生成的邻域半径结果将有所波动．未来的工作将考虑使用结果更稳定的分类方法．

参考文献（References）

［1］"PAWLAK Z. Rough sets［J］. International Journal of Computer amp; Information Sciences， 1982， 11（5）： 341-356.

［2］"HU Qinghua， YU Daren， LIU Jinfu， et al. Neighborhood rough set based heterogeneous feature subset selection［J］. Information Sciences， 2008， 178（18）： 3577-3594.

［3］"娄畅， 刘遵仁， 郭功振. 一种多阈值邻域粗糙集的属性约简算法［J］. 青岛大学学报（自然科学版）， 2014， （4）： 44-48 .

［4］"李冬. 基于邻域粗糙集的属性约简算法研究及应用［D］. 成都： 成都信息工程大学， 2020： 16-19.

［5］"WANG Changzhong， SHI Yunpeng， FAN Xiaodong， et al. Attribute reduction based on k-nearest neighborhood rough sets［J］. International Journal of Approximate Reasoning， 2019， 106： 18-31.

［6］"ZHOU Peng， HU Xuegang， LI Peipei， et al. Online streaming feature selection using adapted neighborhood rough set［J］. Information Sciences， 2019， 481 （2）： 258-279 .

［7］"ZHANG Di， ZHU Ping. Variable radius neighborhood rough sets and attribute reduction［J］. International Journal of Approximate Reasoning， 2022， 150： 98-121.

［8］"PaWLAK Z. Rough sets ［M］. Berlin： Springer Dordrecht， 1991： 10-44.

［9］"LIU Yong， HUANG Wenliang， JIANG Yunliang， et al. Quick attribute reduct algorithm for neighborhood rough set model［J］. Information Sciences， 2014， 271（1）： 65-81.

［10］"巴婧， 陈妍， 杨习贝. 快速求解粒球粗糙集约简的属性划分方法［J］. 南京理工大学学报（自然科学版）， 2021， 45（4）： 394-400.

［11］"DEMIAR J， SCHUURMANS D. Statistical comparisons of classifiers over multiple data sets［J］. Journal of Machine Learning Research， 2006， 7（1）： 1-30.

［12］"DUNN O J. Multiple comparisons among means［J］. Journal of the American Statistical Association， 1961， 56（293）： 52-64.

（责任编辑：曹莉）