问题引领深度学习

笔者通过调查，发现学生学习《分段计费》的困难主要有两点：一是缺乏相关的生活经验，不了解“收费区间”；二是处理复杂信息的能力较弱，对数量关系的把握相对困难。笔者从学生的困难出发设计教学，帮助学生实现知识的有意义建构，发展数学核心素养。

一、用现实的真问题激发学习内驱力

引入环节，笔者呈现如下情境：小明家到游泳馆的距离大约是3千米，他连续两次乘坐同一种型号的出租车走相同的路线，一次停在游泳馆大门口，付费8.5元，一次停在游泳馆大门附近，付费7元。接着，笔者抛出“两次付的钱为什么不一样，是前一位司机多收费了吗？”的问题，启发学生先独立思考，再小组交流，给出合理解释。有的小组提出出租车的起步价可能不一样；有的小组认为出租车收费在整千米以内是一个价格，只要超过整千米就要加钱，并推测第一次的行驶里程可能刚好超过整千米。笔者顺势引入出租车收费标准“3千米以内7元，超过3千米，每千米1.5元（不足1千米按1千米计算）”，并让学生说一说从中得到哪些信息。

二、用关联的问题串突破教学重难点

为帮助学生深入理解问题，笔者深度关注其中的细节，如“基础价”中“3千米以内”究竟指几千米？“超出价”中“不足……按……计算”如何理解？车程与付费之间是什么关系？这些细节探讨的缺失容易导致学生解题出现错误。基于此，笔者设计以下3个关键问题：①什么是分段计费？②关于例9中李叔叔的车费，你赞同谁的想法，为什么？错的方法该怎样调整？③如果出租车一直开下去，费用会如何变化？针对问题的解决，笔者安排以下三个学习活动。

活动一：理解分段计费的含义。呈现例9后，笔者先让学生在学习单上分别用摘录条件和画线段图的方法理解题意，并说一说“3千米以内7元”“超过3千米，每千米1.5元”的意思。接着，笔者依次引导学生说一说李叔叔搭乘出租车行驶1千米、2.1千米、2.9千米、3千米分别应付多少钱，帮助学生理解“3千米以内7元”的含义。然后，笔者呈现学生根据收费标准所画的线段图，并通过提问“线段中间的短竖线代表多少千米？”“为什么要画这条短竖线？”，使学生认识到“3千米”是分界点。最后，笔者小结：两种表示方式虽然不同，但都是以3千米为分界点将出租车行驶里程分成了两部分，每部分的收费标准不同，这就是分段计费问题。

活动二：分析分段计费问题的数量关系。学生在学习单上作答例9后，笔者组织学生交流解决问题的思路和方法：一是列算式分段计算费用；二是“先假设再调整”，即都按每千米1.5元计算费用，再加上前3千米少算的费用。在评价、总结的基础上，笔者引导学生写出数量关系式“3千米以内的价格+超出3千米部分的单价×超出3千米部分的数量=总价”。这样教学帮助学生构建了分段计费问题模型，有利于学生提高迁移能力，发展数学思维。

活动三：渗透函数思想。此环节，笔者引导学生在学习单上填写如下出租车价格表，并观察表中数据。

学生发现前3千米，车费都是7元，3千米以后每增加1千米，车费就增加1.5元。在此基础上，笔者引导学生观察、分析行驶里程与车费之间的关系，使学生体会到两个相关联的量，一个量随着另一个量的变化而变化，从而渗透了函数思想，延伸了教学。

三、用开放的“深问题”拓宽思维空间

在应用与拓展环节，为强化学生分析问题、解决问题的能力，笔者设计了包含三个层次问题的练习题。

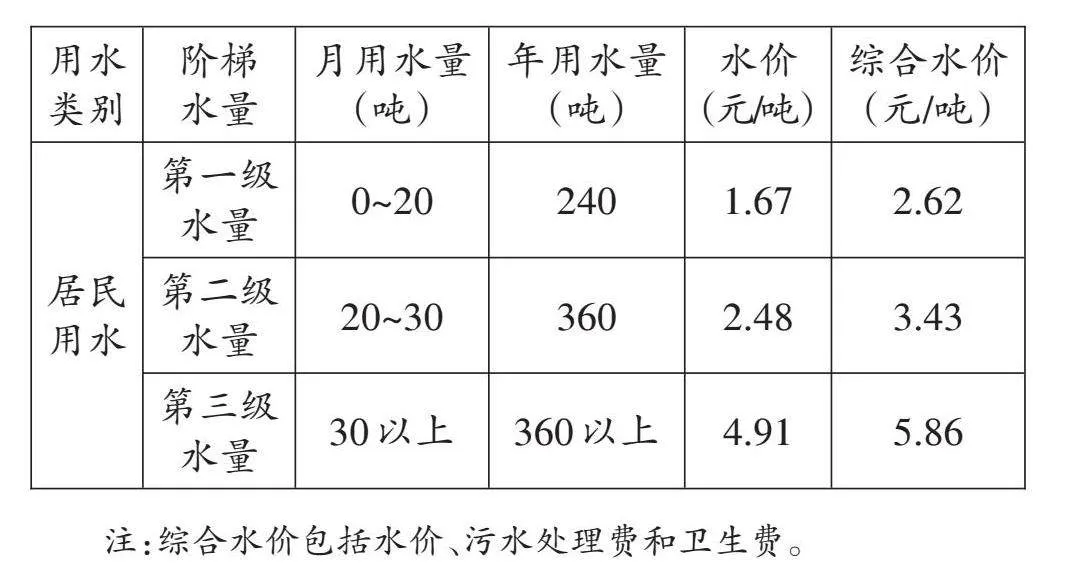
本地居民用水实行阶梯计费，用水量及价格表如下。

①你从表中知道了什么？②按照以上标准，小明家1～8月累计用水量为153吨，他家8月份用水20.7吨，8月份的水费是多少元？（根据本地实际，不足1吨按1吨计算）③比较水费与出租车费的分段计费方式，两者有什么异同？

学生观察表格，在笔者引导下明白了要结合月用水量和年用水量确定每月水价（按综合水价计算，以标准较高的为准），并用所学的分段计费方法解决了小明家8月份用水20.7吨要付72.03元的实际问题。交流作答方法时，笔者相机渗透德育，即分段计费背后既有人文关怀，又有对无节制消耗资源行为的控制，倡导了节约美德。在比较水费与出租车费的分段计费方式时，学生发现：不同点是第一段（级）内出租车按统一价格计费，即有固定的起步价，而水费按单价和实际数量计费；相同点是两种计费方式都按实际数量（里程数、吨数）计费，并且都规定了不足1个计量单位（1千米或1吨）按1个计量单位（1千米或1吨）计算。

上述对比过程中，学生不但通过观察、分析感受到分段计费的特点和规律，初步体会到函数思想，而且挖掘出这样收费的原因，理解了分段计费是生活所需，明确了要合理消费、节约资源。

（作者单位：咸宁市嘉鱼县教学研究室）