多元表征助力分段计费问题教学

分段计费问题是人教版数学五年级上册“小数乘法”单元解决问题领域的内容，是分段函数在现实情境中的具体表现。理解计费标准是解决分段计费问题的关键，而教材中的问题情境以语义表征的形式呈现，较为抽象。为帮助学生实现深度理解和有意义建构，笔者抓住多元表征展开教学。

一、线段图表征，理解分段计费

《义务教育数学课程标准（2022年版）》要求“重视数学内容的直观表述，处理好直观与抽象的关系”，进而说明“几何直观有助于把握问题的本质，明晰思维的路径”。基于此，笔者引导学生将抽象的问题以线段图表征，让学生画线段图分析、理解问题，使抽象的计费标准直观化，以实现深度理解。

教学中，笔者先以教材中出租车收费的问题情境为载体，引导学生围绕计费标准中的“3千米及以内”“超过3千米的部分”“不足1千米按1千米计算”等关键信息展开交流，进而明确：这里的计费标准表达的是行驶里程与车费之间的关系，一段里程以3千米为界分成两段计费，每一段的数量和单价各不相同；行驶里程6.3千米要按7千米计算。接着，笔者引导学生根据交流所得共识画线段图，表示出租车的计费标准。然后，笔者选取学生的典型作品（如图1、图2），引导学生发现两幅作品虽然画法不同，但都是分成两段画的，并且前一段的费用固定不变，后一段的费用随着行驶里程的变化而变化，两段的费用和就是乘坐出租车的总费用。

以上教学，学生通过线段图这一载体将其个性化的思维过程变得可视化，清晰地表示出行驶里程与车费之间的数量关系，建立了分段计费问题的直观模型。同时，直观模型为学生采用多种方法解决问题提供了思路。

二、算式表征，建构数学模型

解决问题时，教师不仅要引导学生用直观的图形解释问题，还要引导学生用抽象的算式解决问题，实现从图形直观到算式抽象的过渡，更好地把握vCHlPRlEL0zZOTiHvbYzFpdtwhzXjH++21SZWjC85A8=问题情境中的数量关系，建构数学模型。

基于学生对计费标准的清晰理解，笔者引导学生列算式表征问题并通过计算解决问题。有了线段图的直观呈现，学生用分两段计算再求和的方法算出了出租车行驶6.3千米的总费用，也就是把6.3千米看作7千米，先用“7-3”算出后一段里程为4千米，再用“1.5×4”算出后一段的费用为6元，最后用前3千米的起步价7元加上后一段的费用6元，得出总费用13元。

随后，笔者让学生继续用此方法计算行驶里程为7.8千米、10.5千米时出租车的总费用。学生正确计算后，笔者引导学生观察不同里程对应的算式，在不断变化的里程和费用中找到不变的关系——“起步价+（总路程－起步路程）×单价=总价”，从而构建分段计费问题的数量关系模型。

在基本模型的基础上，笔者通过唤醒学生已有的“尝试调整”解决问题的经验，引导学生用先假设每千米费用都是1.5元，再加上前3千米少算的费用的方法解决问题。其算式表征如下。

把6.3千米看作7千米。

假设：1.5×7=10.5（元）

少算：7-1.5×3=2.5（元）

应付：10.5+2.5=13（元）

不管是分两段计算再求和还是先假设再调整，两种策略都体现了学生对分段计费问题数量关系的准确把握。最后，笔者引导学生思考两种方法的共性，即在解决问题过程中都抓住了“以3千米为分界线”这个关键点。

三、列表表征，凸显分段界限

列表不但可以清楚地表示行驶里程与费用这两个变量之间的关系，而且能直观呈现以3千米为分界点的两段里程与它们的费用之间的不同关系，从而凸显“分段界限”这一核心要素。

在回顾与反思环节，笔者引导学生采用累加的方法，从1千米开始填写车费，一直填写到7千米，形成完整的表格（如下表）。

之后，笔者追问学生行驶里程为8千米、9千米、10千米的出租车费用。学生在不断向后推算的过程中进一步感受3千米之后费用随着行驶里程的变化而变化。由于表中数据变化特征明显，学生很容易发现其中的规律：前3千米内的费用不变，总是7元；3千米以后，每多1千米就多1.5元。笔者适时引导学生用自己喜欢的方式表示这种变化趋势，学生借助已经学习的折线统计图相关知识，形象地用手势表示。在此过程中，笔者引导学生关注手势的运动轨迹，让学生思考手势应该在什么地方发生变化，从而帮助学生明确变化的节点就是分段计费的分界点——3千米。借助表格中的数据及其变化，辅以直观手势演示，学生进一步理解了分段计费问题的特征，明确了解决分段计费问题的关键在于抓住分界点。

四、图象表征，渗透函数思想

分段计费问题体现了函数关系，为了渗透函数思想，教师可以引导学生依据表格中的数据将行驶里程与车费之间的关系绘制成图象，直观地呈现它们之间的变化关系。

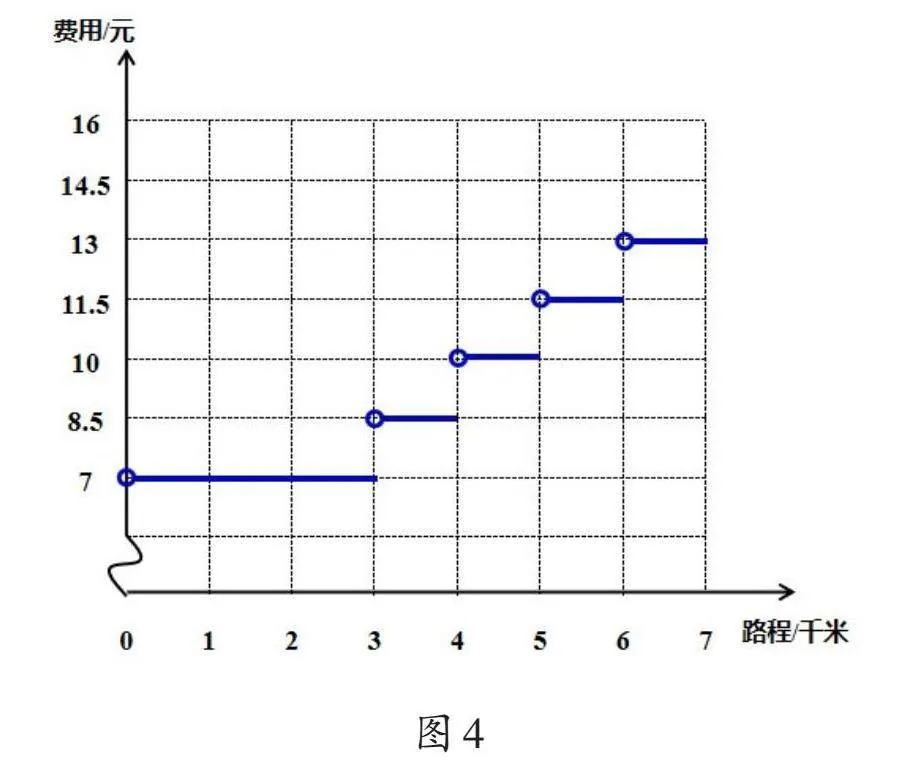
课堂上，笔者先呈现没有标记数据的坐标图，引导学生通过观察，发现横轴代表行驶里程，纵轴代表出租车费。接着，笔者引导：如果把出租车的行驶里程和收费情况在这幅图中表示出来，图象会是什么样呢？笔者示范第一段图象的绘制：0千米代表起点，对应车费为0元，用空心的小圆圈表示；行驶里程在大于0且小于等于3千米的范围内都是7元，在图中以一条平直的线段呈现，代表这一段范围内车费都是7元。然后，学生尝试接着画：由于从3千米开始，每增加1千米就加收1.5元，所以从3千米到4千米这一段都是8.5元，用左端为空心圆的一条短横线表示，以此类推，形成如图4所示图象。

学生在笔者引导下观察图象，发现它一段一段地上升，也就是车费随着行驶里程的增加而增加，并且每段的价格相同。不同的表征形式可以从不同角度呈现和解释分段计费问题的结构，最后，笔者通过沟通线段图、算式、列表和图象四种表征形式，引导学生发现：虽然它们的形式不同，但都在表示第一段（3千米及以内）的起步价不变，第二段（超过3千米的部分）车费随着行驶里程的变化而变化。这样教学，学生不但对分段计费问题形成了全面而又深入的理解，实现了知识的有意义建构，而且感悟到函数思想。

（作者单位：武汉市光谷喻家山学校）