借助图表解决分段计费问题

《分段计费》是人教版数学五年级上册的教学内容，学生探究该类问题能够巩固小数乘法的知识，积累解决问题的经验，为后续学习函数做铺垫。分段计费广泛应用于生活，如出租车费、水费、手机通话费等，教学中，教师不仅要引导学生掌握解决问题的方法和技能，建构数学模型，还要引导学生感悟其中的数学思想方法，并迁移运用所学知识解决生活中的实际问题。本期，我们精选四篇文章，分别从借助图表、多元表征、问题驱动等教学策略和作业设计的视角做具体阐述。

学生学习分段计费问题的难点，一是不能正确理解题意，把握其中蕴含的数量关系；二是缺少解决相关问题的生活经验，认识不到它的社会意义和价值。为帮助学生更加直观地理解分段计费问题，笔者借助图表引导学生明确分段计费的收费标准，探究其中的数量关系，构建分段计费模型并正确解答问题，以增强学生解决问题的能力和节约、环保意识。

一、借助发票图片，初步感知分段计费标准

分段计费是典型的问题解决内容。为激发学生探究的欲望，帮助学生初步感知分段计费的标准，笔者出示如图1所示的8张出租车发票图，引导学生有序整理图片，说一说有什么发现。

学生按照里程数从小到大的顺序排列发票，发现出租车的收费金额和里程数有关系。一名学生说：里程数为0.8千米、1.3千米、2.9千米和3千米时，收费都是7元。另一名学生质疑：“5千米比4千米多1千米，多收1.5元，而3.1千米比3千米只多0.1千米，也要多收1.5元。这是为什么呢？”笔者引导：“猜一猜，出租车是怎样收费的？”有的学生猜测：“里程数在3千米及以内的都是收费7元。”有的学生补充：“这说明出租车的起步价是7元。”有的学生推测：“里程数超过3千米时，每多1千米，就多收1.5元。”又有学生补充：“我猜测最后一段不足1千米的部分按1千米计算。”笔者肯定了学生的想法，并梳理出如下出租车收费标准：3千米及以内7元；超过3千米的部分，每千米1.5元（不足1千米按1千米计算）。随后，笔者出示教材例9：“右面是某地出租车的计价标准。李叔叔乘坐出租车行驶了6.3千米，他应付出租车费多少钱？”学生看到例9中给出的出租车收费标准与他们猜测的一致，兴奋不已，跃跃欲试。

以上教学，笔者从乘坐出租车的生活情境入手，引导学生观察、整理出租车发票图片，提出疑问，猜测出租车的收费标准，激发了学生的探究兴趣。同时，出租车发票为学生感知出租车的收费方式提供了素材，有助于学生发现出租车分段计费的特点。

二、借助画图理解题意，探索分段计费问题解法

画图等直观方法能帮助学生理清问题中的数量关系，探索解决问题的思路并预测结果。因此，教师可引导学生利用数形结合思想，通过画图理解题意，把握数量关系，学会解决分段计费问题。

课堂上，笔者出示例9后提出学习任务：“认真阅读题目，说一说你从中得到了哪些信息。写一写或画一画，用你喜欢的方式表示这些信息。”学生借助已有经验想出了不同的方法：有的学生画简易关系图整理关键信息（如图2），有的学生画线段图整理关键信息（如图3）。

笔者追问：“你是怎样画线段图的？”学生说：“用线段将路程分为两段。第一段表示小于等于3千米的路程，第二段表示超过3千米的路程。因为‘不足1千米按1千米计算’，所以我把6.3千米看成7千米，即线段终点表示7千米。”在此基础上，笔者引导学生对比观察图2、图3的表示方法，学生发现用线段图表示更形象、直观。笔者继续追问：“这两段分别怎样计算费用？”学生根据线段图回答：“第一段只付7元，第二段每多1千米加1.5元。”

笔者提出新任务：“观察整理的信息，思考有哪些解答方法，并用你喜欢的方法解答。”学生独立作答后交流汇报。一名学生说：“6.3千米要按7千米计算，所以第二段超出的部分用‘7-3’计算，得出4千米，再用‘4×1.5’计算出收费6元，最后用6元加上第一段的收费7元，得出要付13元。”笔者引导：“你能给这种方法取个名字吗？说一说理由。”学生稍加思考后说：“分段计算法。这个名字提醒我们要根据不同标准分段计算费用。”另一名学生汇报：“把6.3千米看成7千米，假设7千米都按照每千米1.5元计算，则用“1.5×7”计算出共需支付10.5元。由于前面的3千米也按照每千米1.5元计算，只收了4.5元（1.5×3=4.5），所以应补收2.5元（7-4.5=2.5）。最后用‘10.5+2.5’计算出共付13元。”笔者适时点拨：“我们把这种方法叫做假设法。运用假设法解决问题要注意什么？”学生回答：“要注意补上少算的部分。”笔者小结：“一段里程分成两段收费，这样的计费方式在数学上叫做分段计费。”

这样教学，学生将题目的文字表征转化为图示表征，准确把握了“超过”“不足”等关键词，比较直观地找到了分段的节点，理清了出租车分段计费的原理，最终通过计算解决了问题。

三、表格与图象相结合，构建分段计费模型

分段计费问题实际上是分段函数的体现，教师要借助分段函数图象有效地渗透函数思想，使学生发现分段计费问题中的变与不变，更好地理解与构建分段计费模型。

在回顾与反思环节，笔者引导学生自主完成下面的出租车价格表，建立解决这类问题的一般方法。

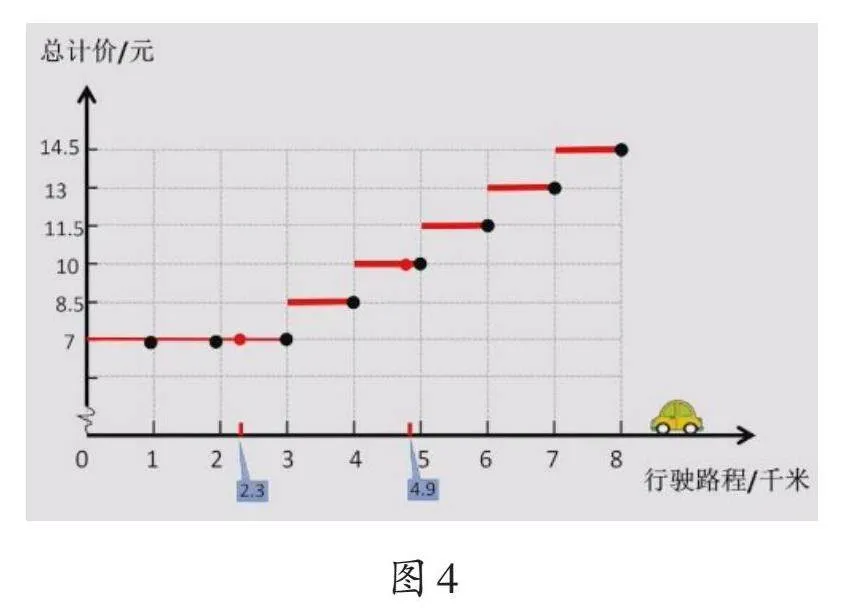
学生根据前面得到的结果填写出租车价格表后，笔者用动画呈现出租车行驶里程和相应车费的变化情况，最终呈现出图4即分段函数图象。

笔者引导：“图4中横着的线叫横轴，表示行驶里程，竖着的线叫纵轴，表示价格。观察图象，你有什么想法？”学生观察后交流：“长一些的红线表示3千米及以内的部分，短一些的红线表示超出的部分。”笔者指着横轴上的2.3追问：“走这么远的路程，车费是多少呢？”学生看图答道：“7元。”笔者再问：“3千米及以内7元是什么意思？”学生回答：“只要车子启动，不超过3千米就付7元。”笔者指着横轴上的4.9继续问：“看短一些的红线，走这么远的路程，车费是多少呢？”学生看图答道：“4.9千米可按5千米计算，5千米比3千米多2千米，要增加2个1.5元，即增加3元，之后用“7+3”计算出应付10元。”笔者引导：“从图象上看，哪一段每千米价格更高？”学生很快发现第一段每千米价格更高。笔者小结：“分段计费的每一段就像一个阶梯，所以又称为‘阶梯收费’。”

这样教学渗透了函数思想，帮助学生更好地理解与建构了分段计费模型。

（作者单位：老河口市实验小学）