基于直观想象能力发展的立体几何教学研究

［摘 要］ 几何直观感知是形成与发展理性思维的基础，而理性思维的形成与发展又是催生空间想象力的关键，直接影响直观想象能力的发展. 因此，几何教学对提升学生直观想象能力至关重要. 研究者以“直线与平面垂直的判定”为例，从教学分析、教学过程与教学思考三方面，探究直观想象能力在立体几何教学中的发展.

［关键词］ 直观想象；几何教学；线面垂直

直观想象是指通过几何直观与空间想象来感知事物具体的形态与变化，用图形理解并解决问题的过程. 高中阶段的立体几何教学侧重分析事物的空间形态、位置关系和运动规律，通过直观感知和推理论证探索空间图形，以发展学生的几何直观和空间想象素养. 究竟该如何实施立体几何课堂教学，培养学生的直观想象能力呢？

教学分析

1. 问题分析

学生在本节课前接触过线线垂直，掌握了直线与平面平行的定义与性质，并有操作、观察、抽象、总结等学习经验. 因此，学生具备一定的几何直观、空间想象和推理论证等能力，且对直线与平面垂直有认知经验. 但在实际学习过程中，仍存在一些共性问题：

（1）通过折纸活动抽象直线与平面垂直的判定定理，理解定义中的“任一条直线”和判定定理中的“两条相交直线”的内涵，用“有限”替代“无限”，让不少学生感到困惑.

（2）学生虽然具备一定的空间想象与推理论证能力，但都不够成熟. 在直线与平面垂直的定义与判定定理的研究中，学生无法灵活选择平面内的两条相交直线来推导直线与平面的垂直关系. 同时对于证明直线与直线垂直，选取与直线垂直的平面作为辅助也没有清晰思路.

从上述问题来看，可确定本节课的教学重点与难点在于：探索并抽象直线与平面垂直判定定理，实现定义与判定定理在解决线面垂直问题时相互转化.

2. 条件分析

支持本节课教学的工具有多媒体课件、表示直线的铅笔、表示平面的课本、三角板和彩色三角形卡纸.

教学简录

1. 提炼定义

（1）联系生活，提出问题

课堂伊始，教师带领学生一起回顾直线与平面平行的相关知识与研究方法. 展示升国旗的图片，要求学生说一说旗杆与地面存在怎样的位置关系. 基于学生回答，要求学生自主分析直线与平面垂直的定义.

设计意图 旧知回顾为新知探索奠定方法基础，学生通过观察现实生活图片，初步感知直线与平面的垂直关系，并在好奇心的驱使下，积极参与本节课探索活动. 这是一个承上启下的引入环节，揭露本节课的研究主题.

（2）活动探索，初步感知

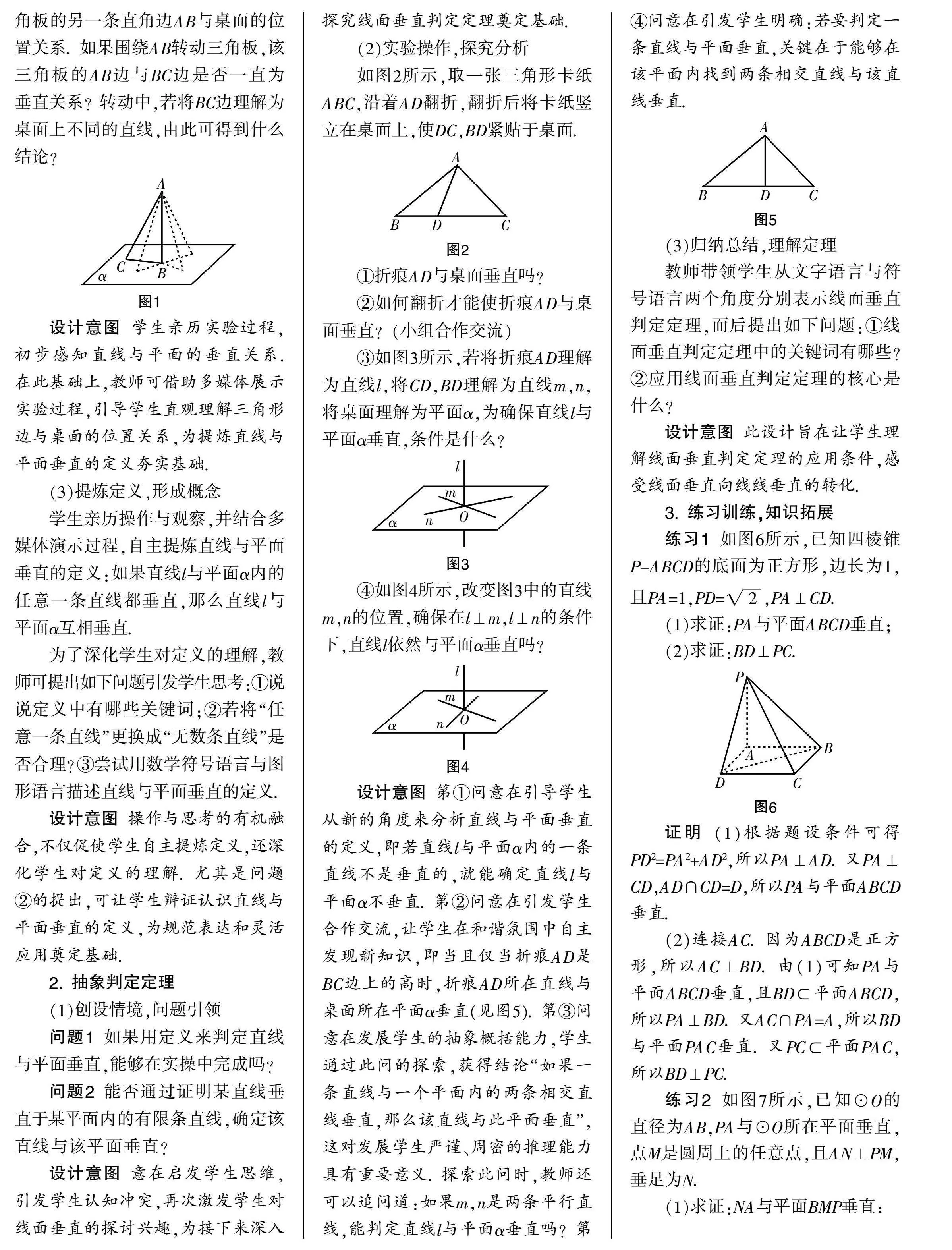
如图1所示，将三角板的一条直角边BC紧贴桌面竖立起来，观察三角板的另一条直角边AB与桌面的位置关系. 如果围绕AB转动三角板，该三角板的AB边与BC边是否一直为垂直关系？转动中，若将BC边理解为桌面上不同的直线，由此可得到什么结论？

设计意图 学生亲历实验过程，初步感知直线与平面的垂直关系. 在此基础上，教师可借助多媒体展示实验过程，引导学生直观理解三角形边与桌面的位置关系，为提炼直线与平面垂直的定义夯实基础.

（3）提炼定义，形成概念

学生亲历操作与观察，并结合多媒体演示过程，自主提炼直线与平面垂直的定义：如果直线l与平面α内的任意一条直线都垂直，那么直线l与平面α互相垂直.

为了深化学生对定义的理解，教师可提出如下问题引发学生思考：①说说定义中有哪些关键词；②若将“任意一条直线”更换成“无数条直线”是否合理？③尝试用数学符号语言与图形语言描述直线与平面垂直的定义.

设计意图 操作与思考的有机融合，不仅促使学生自主提炼定义，还深化学生对定义的理解. 尤其是问题②的提出，可让学生辩证认识直线与平面垂直的定义，为规范表达和灵活应用奠定基础.

2. 抽象判定定理

（1）创设情境，问题引领

问题1 如果用定义来判定直线与平面垂直，能够在实操中完成吗？

问题2 能否通过证明某直线垂直于某平面内的有限条直线，确定该直线与该平面垂直？

设计意图 意在启发学生思维，引发学生认知冲突，再次激发学生对线面垂直的探讨兴趣，为接下来深入探究线面垂直判定定理奠定基础.

（2）实验操作，探究分析

如图2所示，取一张三角形卡纸ABC，沿着AD翻折，翻折后将卡纸竖立在桌面上，使DC，BD紧贴于桌面.

①折痕AD与桌面垂直吗？

②如何翻折才能使折痕AD与桌面垂直？（小组合作交流）

③如图3所示，若将折痕AD理解为直线l，将CD，BD理解为直线m，n，将桌面理解为平面α，为确保直线l与平面α垂直，条件是什么？

④如图4所示，改变图3中的直线m，n的位置，确保在l⊥m，l⊥n的条件下，直线l依然与平面α垂直吗？

设计意图 第①问意在引导学生从新的角度来分析直线与平面垂直的定义，即若直线l与平面α内的一条直线不是垂直的，就能确定直线l与平面α不垂直. 第②问意在引发学生合作交流，让学生在和谐氛围中自主发现新知识，即当且仅当折痕AD是BC边上的高时，折痕AD所在直线与桌面所在平面α垂直（见图5）. 第③问意在发展学生的抽象概括能力，学生通过此问的探索，获得结论“如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直”，这对发展学生严谨、周密的推理能力具有重要意义. 探索此问时，教师还可以追问道：如果m，n是两条平行直线，能判定直线l与平面α垂直吗？第④问意在引发学生明确：若要判定一条直线与平面垂直，关键在于能够在该平面内找到两条相交直线与该直线垂直.

（3）归纳总结，理解定理

教师带领学生从文字语言与符号语言两个角度分别表示线面垂直判定定理，而后提出如下问题：①线面垂直判定定理中的关键词有哪些？②应用线面垂直判定定理的核心是什么？

设计意图 此设计旨在让学生理解线面垂直判定定理的应用条件，感受线面垂直向线线垂直的转化.

3. 练习训练，知识拓展

练习1 如图6所示，已知四棱锥P-ABCD的底面为正方形，边长为1，且PA=1，PD=，PA⊥CD.

（1）求证：PA与平面ABCD垂直；

（2）求证：BD⊥PC.

证明 （1）根据题设条件可得PD2=PA2+AD2，所以PA⊥AD. 又PA⊥CD，AD∩CD=D，所以PA与平面ABCD垂直.

（2）连接AC. 因为ABCD是正方形，所以AC⊥BD. 由（1）可知PA与平面ABCD垂直，且BD⊂平面ABCD，所以PA⊥BD. 又AC∩PA=A，所以BD与平面PAC垂直. 又PC⊂平面PAC，所以BD⊥PC.

练习2 如图7所示，已知☉O的直径为AB，PA与☉O所在平面垂直，点M是圆周上的任意点，且AN⊥PM，垂足为N.

（1）求证：NA与平面BMP垂直；

（2）如果AQ⊥PB，Q为垂足，求证：NQ⊥PB.

证明 （1）由于AB为☉O的直径，因此AM⊥BM. 由于PA与平面BMA垂直，因此PA⊥BM. 又PA∩AM=A，所以BM与平面PAM垂直. 因为AN⊂平面PAM，所以BM⊥AN. 由AN⊥PM，PM∩BM=M，可得AN与平面BMP垂直.

（2）由（1）问可知，AN与平面BMP垂直，结合PB⊂平面BMP，可得PB与平面ANQ垂直. 又NQ⊂平面ANQ，所以NQ⊥PB.

设计意图 上述两个练习意在引导学生灵活转化与融合新旧知识，感知转化思想在解决实际问题中的重要性. 通过积极思考与讨论，实现不同层级的发展.

4. 归纳总结，完善认知

师：说说你们在本节课中学到的数学知识、数学方法和数学思想.

学生回顾直线与平面垂直的定义与判定定理，并从数学知识、数学方法和数学思想三方面展开分析，构建思维导图（如图8所示）.

设计意图 该过程旨在培养学生归纳、总结与反思能力，引导学生从宏观角度审视学习成果，巩固知识，为发展核心素养打基础.

教学思考

教师从明暗双线展开教学，明线为直线与平面垂直的定义、判定定理及应用情况；暗线是上述过程所蕴含的转化与化归思想. 从直线与平面垂直的定义到判定定理的探究，展现了从抽象到具体的转化，揭示了从空间到平面的化归，凸显了线线垂直与线面垂直的关系.

课程遵循“直观感知—操作确认—归纳总结”的流程，通过紧密相连的活动，引领学生思维向纵深发展. 课堂贯彻“以生为本”理念，从旗杆问题的引入到直线与平面垂直的定义和判定定理的探索，鼓励学生自主思考、合作研究. 在和谐民主的氛围中，学生积极参与，锻炼直观想象素养.

总之，数学教学是一种艺术. 教师应更新教学理念，紧跟时代，基于学情设计教学方案，这是发展学生数学学科核心素养、培养学生可持续发展能力的重要途径.