变化中窥发展 比较中寻优化

［摘 要］ 基本不等式是高中数学的重要内容之一，对探寻最优方案解决实际问题大有裨益，能有效连接数学与现实生活. 采用比较研究法，详细分析北师大版高中数学新旧教材中基本不等式的课标要求、知识编排、数学文化及例习题设置，利于新一轮教材编撰及教学策略优化. 基于研究结果提出三点教学建议：基于整体观念调整“大单元”教学内容；以数学文化为“引”发挥真实效能；推进例习题设计多样化.

［关键词］ 高中数学教材；基本不等式；北师大版；比较研究

引言

教材的编写与研究是教材建设工作相互联系的两个方面，前者为后者提供素材并展现其成果和水平，后者则为前者提供科学基础昭示其改进方向［1］. 随着《普通高中数学课程标准（2017年版2020年修订）》的发布，新教材编撰再起波澜. 因此，研究教材变迁，了解其发展与应用至关重要.

研究对比北京师范大学出版社于2011年和2019年出版的普通高中数学教科书（2011年出版的教科书简称旧教材，2019年出版的教科书简称新教材）中的基本不等式内容，原因有二：其一，基本不等式是高中数学联系生活的重要桥梁，蕴含丰富的数学文化素材，涉及众多数学思想方法. 随着教育改革的推进，以及课程标准的更新换代，基本不等式相关内容更迭不断，相较于基本不等式的教学、证明和应用研究，教科书方向的研究较少. 其二，国内数学教材比较研究多关注人教版，然其他版本教材亦有众多可取之处. 北师大版是除人教版外使用范围最广的教材，曾获国家教材委员会主办、教育部承办四年一次的“全国优秀教材（基础教育类）”二等奖［2］. 研究拟从比较视角分析课标要求、知识编排、数学文化和例习题设置，明晰“基本不等式”内容在新旧教材变迁中的变化，以期以小见大，助力研究者掌握数学教材变革动向，并为新一轮教材编撰及一线教师合理使用教材提供参考借鉴.

研究内容与结果分析

1. 课标要求

课程标准是教材编写和修订的依据，因而剖析不同时期的课程标准利于明晰教材在改版过程中的编排脉络与变革动向. 对比《普通高中数学课程标准（实验）》（下文简称旧课标）与《普通高中数学课程标准（2017年版2020年修订）》（下文简称新课标）对基本不等式的要求如表1所示.

从内容要求来看，新旧课标均对“内涵理解”与“公式应用”提出了要求. 就第一点而言，新课标对基本不等式行为动词的要求从“探索并了解”提升为“掌握”，强调学习者需深入理解数学对象的本质特征. 而从第二点来看，新旧课标均强调学以致用，但新课标特别注重“结合具体实例”，强化理论与实践的结合.

新旧课标均未对基本不等式作单独提示，而是归入“不等式”大类描述. 旧课标主要阐明不等式是刻画区域的重要工具，而新课标则更注重数学思想方法的渗透，以及等式与不等式的共性与差异的探索.

从学业要求来看，旧课标未具体规定，新课标则重视核心素养目标，切合党的教育方针，强调教材在立德树人方面的价值.

2. 知识编排

（1）章节设置

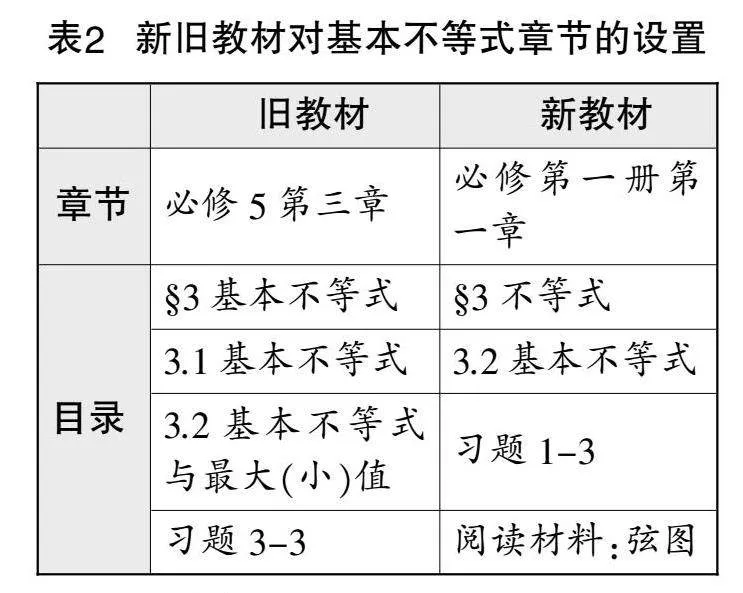
如表2所示，基本不等式在新旧教材中均属必修内容，但旧教材中的基本不等式位于必修末尾（必修5），而新教材则将基本不等式移至必修第一册第一章“预备知识”中，必修地位有所提升. 小学、初中初步学习了不等式，高中前置基本不等式，强化课程衔接，为后续学习函数最值奠定了基础. 因此，教材修订基本不等式章节，使学习顺序更符合学生的认知发展水平.

（2）栏目设置

教材中的栏目是表征知识的一种方式，也是体现教材建构特色的一种形式，蕴含着丰富的教育教学价值［3］. 统计并比较新旧版教材的栏目设置，以明晰其编写特色及异同（结果如表3所示）.

由表3可知，新旧教材均设置“思考交流”“阅读材料”栏目，表明教材编写注重学生拓展性思维的发展. 新教材将“小资料”栏目归入同类的“阅读材料”栏目，优化栏目编排设计. 同时，新教材在借鉴旧教材编排经验的基础上，新增了“实例分析”和“抽象概括”两个栏目，强调学生自主探究和数学抽象素养的培养，促进学生通过实践操作检验知识，加强数学与生活的联系，提升学生分析和解决问题的能力.

3. 数学文化

（1）数学文化分类

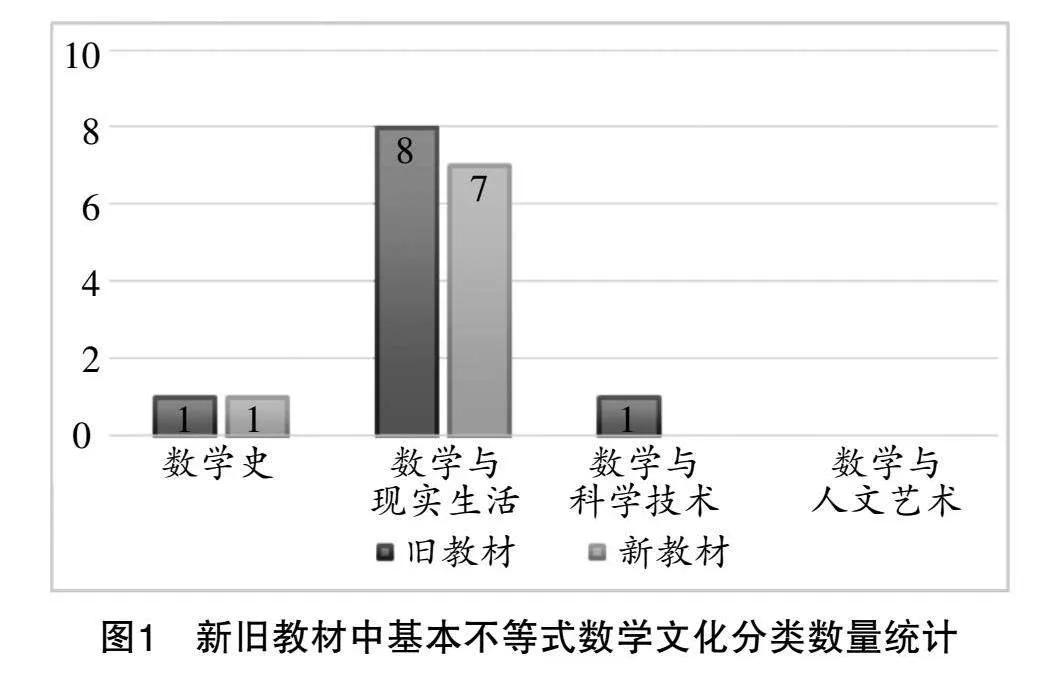
新旧课标均注重数学文化的渗透和价值体现［4］［5］. 借鉴王建磐和汪晓勤对数学文化的界定［6］，以新旧教材为例进行概括说明（见表4），并统计新旧教材中基本不等式数学文化的分类数量（见图1）.

由图1可知，两版教材基本不等式数学文化以“数学与现实生活”为主，其他类别较少，且均未提及“数学与人文艺术”，分布不均. 新教材基本不等式内容总页数（7页）少于旧教材（10页），说明其数学文化分布密度略大于旧教材.

（2）数学文化运用方式

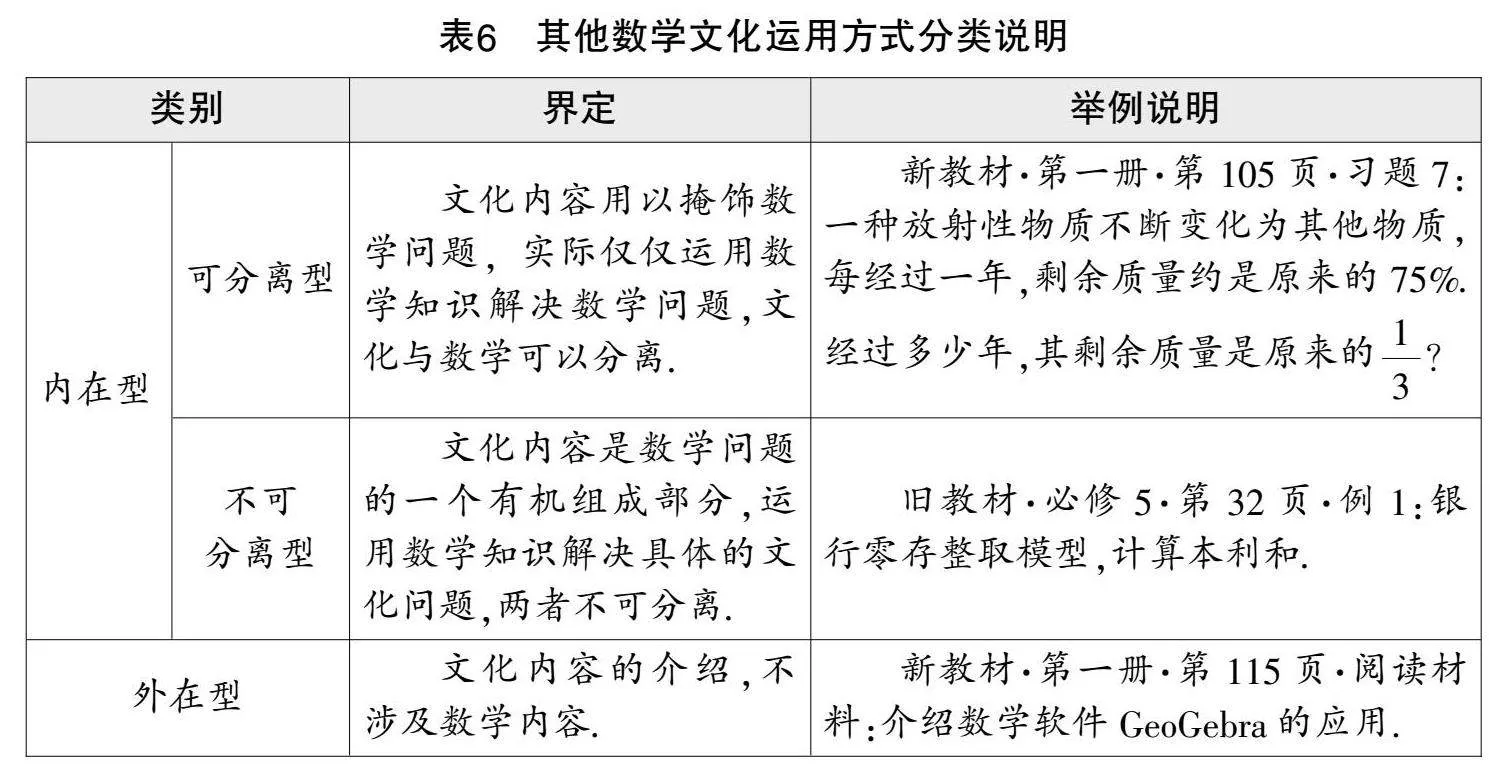
按数学文化与数学知识的关联程度，数学史的运用方式分为五类：点缀式、附加式、复制式、顺应式和重构式［7］（见表5）. 其他数学文化的运用方式可分为外在型和内在型（内在型又可细分为可分离型和不可分离型）［8］（见表6）.

如图2、图3所示，新旧教材均将赵爽弦图史料置于节末，关联国际数学家大会会标，让史料有效链接现实. 其文字部分属于重构式，与数学知识的关联度较高；图片部分属于点缀式. 经统计，基本不等式内容中其他数学文化的运用方式大多属于可分离型（见表7），与数学知识的关联度较低，即去掉数学文化背景也不影响数学问题的解决.

4. 例习题设置

（1）例习题数量

习题分为练习题（栏目标题带有“练习”二字）、课后习题（栏目标题带有“习题”二字）和复习题（通常出现于章末，涉及一章所有知识点）. 规定例习题的题量以小题数量为准：每一例习题出现一次计题量为1；若一大题包含4个小题且小题间无绝对关联性，则计题量为4，否则为1；若一大题不包含任何小题，则计题量为1；若一小题存在多问，也计题量为1. 基于上述规定，对基本不等式相关例习题数量进行统计，如表8所示.

基本不等式在旧教材中共6道例题、15道习题，在新教材中共3道例题、21道习题. 通过比较可知，新教材中的例题减少了而习题增加了，更考验学生的知识转化与迁移能力. 此外，两版教材的习题均设置为A组、B组，体现难度的分层设计，关注学生的差异性.

（2）例习题内容

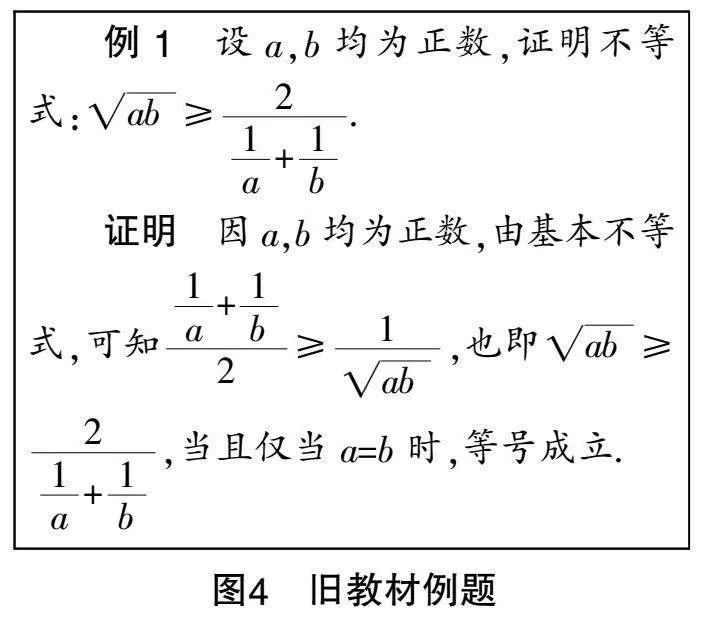
新旧教材在例习题内容设置上也有所差异. 如图4、图5所示，旧教材将基本不等式相关知识点置于例题中，并给出证明过程；而新教材则将其置于习题中，不给证明过程，对学生的自主学习能力提出了更高的要求.

（3）例习题综合难度

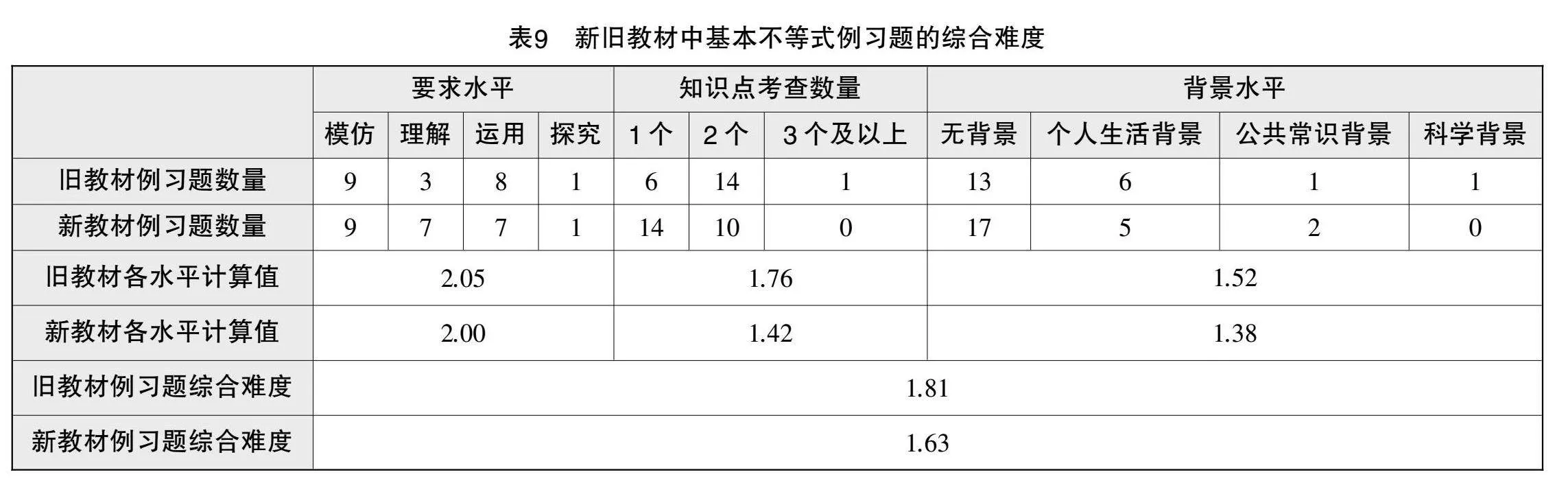
为深入了解基本不等式的例习题设置特征，借鉴吴立宝、王建波、曹一鸣［9］构建的难度分析框架，分别从要求水平（模仿、理解、运用、探究）、知识点数量（1个、2个、3个及以上）和背景水平（无背景、个人生活背景、公共常识背景、科学背景）三个维度进行统计，依据公式计算难度，结果保留两位小数，如表9所示.

由表8、表9可知，虽然新教材中的例习题更多，但难度小于旧教材，表明教材沿革中，例习题对学生掌握知识程度的考查趋向基础性. 就要求水平而言，新教材计算值小于旧教材，且两版教材均较少设置探究类例习题；在知识点考查数量上，新教材计算值小于旧教材，且对1个知识点的考查居多，而旧教材主要考查2个及以上知识点；从背景水平来看，新教材计算值小于旧教材，两者多设置无背景例习题（即纯数学背景），表明教科书的编排始终重视数学知识本身，且有背景的例习题均以个人生活为主，科学背景较少. 总体而言，新教材在各个维度的计算值均小于旧教材，可见教材对例习题各维度的变迁趋向一致.

研究总结与建议

通过比较北师大版高中数学新旧教材基本不等式内容，洞察教材发展趋势，提出三点建议，助力教师教学和教材编撰.

1. 基于整体观念调整“大单元”教学内容

建构主义的学习观强调应把学习者原有的知识经验作为新知识的生长点，引导学习者从原有的知识经验中，生长新的知识经验［10］. 因此，对教育教学而言，知识过渡与衔接尤为重要. 新教材对基本不等式内容的调整可见一斑，其将基本不等式置于“预备知识”处，能有效衔接初中不等式与高中函数最值的学习.

基于此，教师教学时应立足课程标准，尊重学生的认知发展规律，在整体观念下进行“大单元”教学设计. 基本不等式需要较高的抽象思维能力，而一元二次不等式与初中知识紧密相关. 为加强学生对数学思想方法的理解，建议将基本不等式教学置于一元二次不等式之后，以便学生更好地理解和应用新知识. 旧教材对这两类专题的位置设计便是如此，教师可基于班级学情和自身教学能力进行考量.

2. 以数学文化为“引”发挥真实效能

近年来，学术界对数学文化的研究盛行，但需警惕误区：将添加“星点”文化素材视为融入. 就基本不等式数学文化的比较结果而言，新旧教材对数学文化的分布不均，多为“数学与现实生活”类，可见两版教材对数学文化素材的使用有限，且除史料用重构式呈现外，其他数学文化素材多属可分离型，与数学知识的关联程度较低，不利于发挥文化育人之效.

笔者通过访谈得知，教师和学生普遍担忧“课前引入”会浪费课时，但直给式的知识迁移又显枯燥乏味且不利于记忆，因而如何发挥引入实效成了亟待考量的难题. 事实上，除教材呈现的赵爽弦图外，古今对基本不等式的探索、求解比比皆是. 如“欧拉羊圈”是等周面积最值问题的典型例子，作为探究性引入素材恰可衔接基本不等式，既有趣又易记，还重视知识发生和发展的过程. 现有数学文化素材可改编，如旧教材必修5以第24届国际数学家大会会标（根据赵爽弦图设计）为背景，设置探究题引入基本不等式，是优秀改编案例.

3. 促进例习题多样化设计

例习题是数学教材的重要组成部分，有思维能力训练、思想方法渗透、诊断反馈补救与育人等功能［11］. “一正、二定、三相等”是求解大多数基本不等式题的先决条件，而学生往往“知其然不知其所以然”. 建议增加改错题，以丰富题型，由学生自主纠错，强化知识点的学习，确保逻辑链完整.

窥一斑而知全豹，通过对例习题的多维度综合比较，可知基本不等式各维度计算值及综合难度均有所降低，说明教材重视基本不等式知识内容的基础性，满足课程标准的要求. 但随着知识经济时代的到来，时代性与发展性备受关注，因此例习题的多样化设计应纳入考量. 就北师大两版高中数学教材关于基本不等式例习题而言，在要求水平上更多强调模仿与理解，较少设置探究类例习题，而探究恰是激发学生学习动力的有效途径，故需在此加强例习题的多样化设计. 值得注意的是，两版教材例习题均缺背景，即使有背景，也多限于个人生活，公共常识与科学背景寥寥无几. 基本不等式作为不等式学习的重要一环，不仅在数学上有广泛应用，也深度融入物理、化学、地理等学科. 因此，问题情境的选择应放眼至古今中外，从习题本身出发切实提升人文与应用价值，由此提高学生跨学科思维水平，真正达到例习题学以致用的效能. 需要注意的是，例习题的多样化设计指向教育质量的提升，切不可舍本逐末.

参考文献：

［1］ 曾天山.教材论［M］. 南昌：江西教育出版社，1997.

［2］ 中华人民共和国教育部.国家教材委员会关于首届全国教材建设奖奖励的决定［EB/OL］. （2021-10-9）［2022-12-1］. https：//www.moe.gov.cn/srcsite/A26/s8001/202110/t20211012_571686.html.

［3］ 张定强，梁会芳，杨怡. 数学学科核心素养导向的“三角函数”教材内容变革［J］. 数学通报，2021，60（12）：4-7.

［4］ 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［5］ 中华人民共和国教育部.普通高中数学课程标准（实验）［M］. 北京：人民教育出版社，2003.

［6］ 王建磐，汪晓勤，洪燕君. 中、法、美高中数学教科书中的数学文化比较研究［J］. 教育发展研究，2015，35（20）：28-32+55.

［7］ 汪晓勤. HPM：数学史与数学教育［M］. 北京：科学出版社，2017.

［8］ 沈春辉，柳笛，汪晓勤. 文化视角下“中新美法”四国高中数学教材中“简单几何体”的研究［J］. 数学教育学报，2013，22（4）：30-33+102.

［9］ 吴立宝，王建波，曹一鸣. 初中数学教科书习题国际比较研究［J］. 课程·教材·教法，2014，34（2）：112-117.

［10］ 莱斯利·P.斯特弗，杰里·盖尔. 教育中的建构主义［M］. 高文，徐斌燕，程可拉，等，译. 上海：华东师范大学出版社，2002.

［11］ 吴立宝，王富英. 数学教材习题“七功能”［J］. 教学与管理，2014（31）：66-68.