基于改进遗传算法的电商零售商家库存优化研究

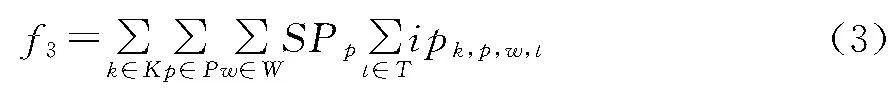
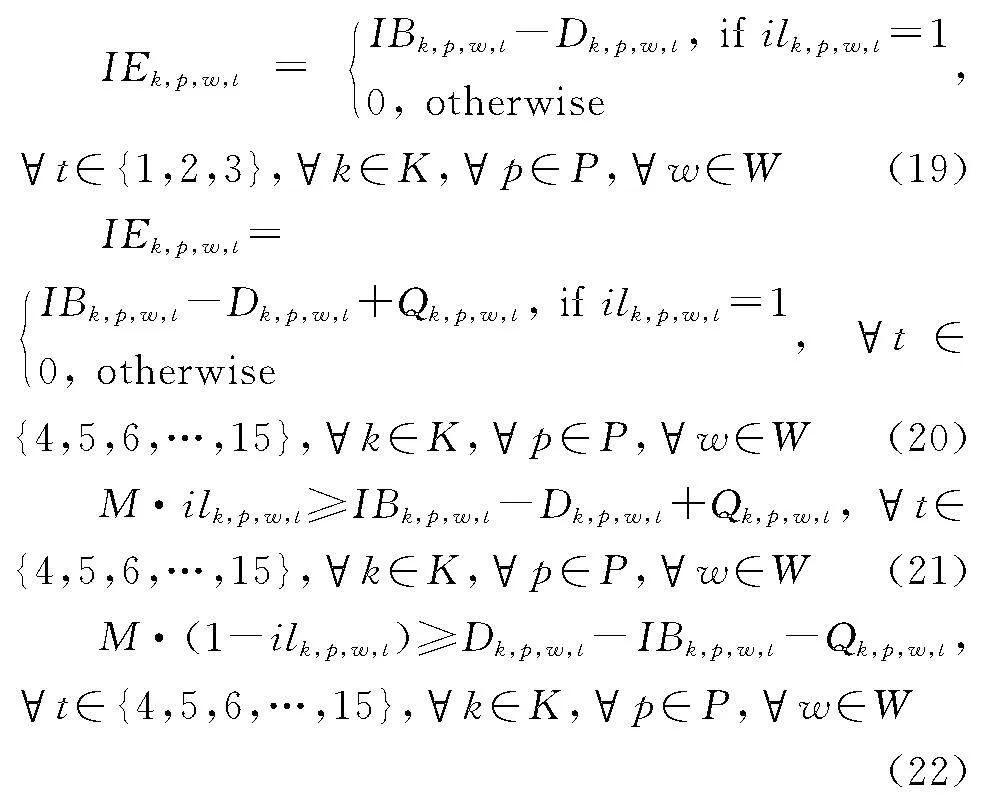
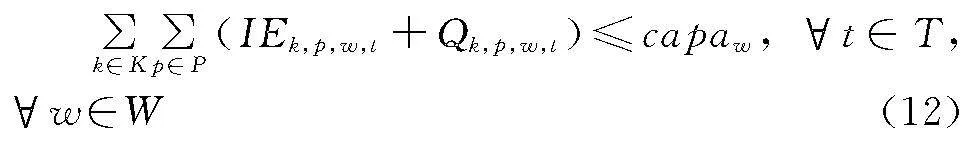
摘 要： 库存优化指为应对需求不确定性，考虑订货点和交货期因素，降低库存系统成本。本文首先构建数学规划模型，将安全库存水平策略（s、S）和每日补货量作为核心决策变量，目标是最小化库存总成本（持有和缺货成本）、库存周转天数订购成本，然后引入0-1辅助变量线性化处理非线性约束，并使用Gurobi和COPT两种求解器对模型进行数值分析和比较，同时进一步提出改进遗传算法在库存优化中的应用，开创性地设计新颖的编码方式，有效增强求解的效率和准确性。算例表明，此库存优化降低了需求不确定性，能灵活应对零售需求中多种需求模式，并针对（s，S）政策与优化的库存持有量和订单数量相结合，实现了最低的库存成本和周转天数，最终实现高效的库存管理和采购决策。

关键词： 库存优化；数学规划；Gurobi；COPT；改进遗传算法

中图分类号： F 713

文献标志码： A

Research on Inventory Optimization of E-Commerce RetailMerchants Based on Improved Genetic Algorithm

Abstract： Inventory optimization refers to reducing the cost of inventory system by considering the factors of order point and delivery time to deal with the uncertainty of demand. This paper first constructs a mathematical planning model， taking the safety inventory level strategy （s， S） and daily replenishment volume as the core decision variables， with the goal of minimizing the total inventory cost （holding and out costs） and the ordering cost of inventory turnover days. Then 0-1 auxiliary variables are introduced to linearize the nonlinear constraints， and Gurobi and COPT solvers are used to numerically analyze and compare the models. At the same time， the application of genetic algorithm in inventory optimization is further proposed， and a novel coding method is designed in a pioneering way to effectively enhance the efficiency and accuracy of solution. The example shows that this inventory optimization reduces the demand uncertainty， flexibly responds to multiple demand patterns in retail demand， and combines the （s，S） policy with the optimized inventory holding and order quantity to achieve the lowest inventory cost and the number of inventory turnover days， and finally realizes efficient inventory management and purchasing decisions.

Key words： inventory optimization; mathematical programming; Gurobi; COPT; improved genetic algorithm

0 引言

随着电子商务的快速普及与发展，电商企业的订单不断呈现出小批量、多批次、差异化的特点。在激烈变化的市场竞争环境下，库存管理作为一个必要手段，为企业创造了可持续竞争优势，合理的库存管理策略能够在保持较高客户服务水平的同时，有效控制企业库存水平，创造更多利润。电子商务愈来愈注重消费者体验，同时消费者的不确定需求影响着供应链管理的物流、信息流、资金流，进而影响企业的效益。其中，库存控制是提高企业利润空间的重要手段之一。

电商零售商优化库存问题，引起了国内外学者的重视。Acimovic和Graves考虑在电子商务背景下对联合库存进行补货和调配，该研究以运输成本最优为原则，通过启发式的方式进行决策，鲁棒性较好。Heissi和Sethuraman解决多家零售商联合补货的问题，建立博弈模型，在多家零售商之间实现补货均衡，根据事先通知零售商的调配决策，使零售商能够在较小的成本下做出补货决策。Protopappa-Sieke等人解决制造商和零售商之间的调拨和补货问题，通过建立供应合同，实现更好的调拨和补货决策。Tinoco和Creemers研究了两家企业协作运输的补货模式，使两家企业在着重考虑运输成本的前提下同步补货，通过建立模型来支持补货和分配决策。Stenius和Karaarslan研究一个配送中心对多家零售商的补货和调拨决策，通过数学计算推导出每个零售商水平的准确概率分布和其他库存信息，从而求解订货提货前期的补货和调拨决策。

国内的学者们在库存优化方面也取得了一些成果。王林与郑贵莲等人基于资源有限和数量折扣考虑配送中心选址，构建联合补货模型，在模拟退火算法的基础上求解联合补货的方法，使得库存总成本降低。宋世强在冷链中解决二级冷库的补货和调配问题，研究基于两个冷库之间的补货和提前期，在两个冷库中采用不同的补货策略，有效优化安全库存。艾学轶与张金隆等人建立联合调拨非即时变质品的模型，通过迭代算法对变质后的补货和调拨进行决策，最终实现非即时变质品变质率的有效降低。成诚与左传等人对供应商的短期折扣、特殊补货，在结合经济订货批量的前提下，建立效益最大化模型，应用全局优化算法，检测和研究库存补货决策的有效性。董琪与徐廷学针对多层次库存网络，考虑多层次库存之间的分配问题，构建库存优化模型，利用迭代算法和解决分配决策软件进行分配决策，有效控制库存成本。曹斌斌与孙静春等人采用线性补货策略，针对有补货提前期的供应链节点进行管理，有效抑制了牛鞭效应的产生。

上述学者充分了解库存优化的重要性，但对于库存优化策略和算法优化却较少有研究。本文旨在探讨电商零售商家库存优化问题的解决方案，通过构建库存优化的策略和模型，运用改进的遗传算法，关注于如何制定有效的库存管理策略，并分析不同参数（持有成本、库存成本、订购费用）对不同需求模式商品补货计划的影响。本文的目标是为电商零售商提供一个综合的参考框架，帮助他们在竞争激烈的市场环境中作出更明智的决策。

1 问题描述

本文的补货计划是指按固定的库存盘点周期NRT=1，对每个商品决策应采购多少货物。其中所有商品期初库存均为5，且采购提前期LT=3，即采购的货物只能在LT天后到达。商品的持有成本及缺货成本均与商品价格正相关，基于周期性盘点库存策略（s，S）、需求量，给出商家历史出货量范围内仓库及商品在 2023年5月16日至 2023年5月30日的补货计划，目标是降低成本，提升服务水平，并降低库存周转天数。

（1）数据预处理：商品价格数据表中给出了1191种商品的价格，结合商家历史出货量中给出的销售数据，进行商品筛选和数据拼合，得到1957条SKU数据，对应34个商家、1191种商品和54个仓库。考虑商品的持有成本、库存成本、商品本身的价格正相关，为了判断不同类型商品的持有成本、缺货成本对总成本的影响，根据商品价格和序列类别划分为四类，其中价格划分按照排序后商品价格分布情况，划分为low、medium、high、veryhigh，序列类别划分则按照SBC分类法将商品划分为intermmitent、Lumpy、Erratic、Smooth。

（2）模型建立：建立整数规划模型来计算最优的补货策略，主要考虑的目标函数是商品的持有成本、缺货成本、订购成本和库存周转天数，并采用服务水平衡量模型求解结果的可靠性。考虑的约束主要包含库存更新约束、缺货约束、采购约束、仓库容量约束和期初库存约束。由于模型在建立阶段会出现非线性表达式，如当执行（s，S）补货策略时，库存水平低于订购点s时，商品采购量为最大库存S减去当前库存水平，否则为0，此时的采购量为分段函数形式且受到其他变量的影响，因此需要对模型进行线性化处理。

（3）模型灵敏度分析：假设持有成本和缺货成本与商品价格正相关，但是不同商品的持有成本、缺货成本对目标函数取值的影响是不同的，且不同的订购成本对总成本的影响也是不同的，因此本文将组合不同类别商品的持有成本率、缺货成本率、订购价格的变化情况，研究补货策略的变化情况。

通过以上三个步骤，本文旨在给出低成本、高服务水平、低库存周转天数下的补货策略，帮助商家进行采购、销售和运营。

2 模型建立

2.1 符号说明

2.2 模型假设

该模型的假设主要包括成本、审查期、提前期、库存四个方面，具体如下：

假设1：商品的持有成本和缺货成本均与商品的价格成正比。

假设2：商品的持有成本系数与缺货成本系数的和为1。

假设3：每种商品的订购成本与商品的价格成正比。

假设4：库存周期内的订货点和最大库存水平为同一值，不随时间变化。

假设5：商家在期末进行库存盘点，并决定是否进行采购。

假设6：交货期是确定的，不存在订单交叉现象。

假设7：每次订购的商品经过提前期时间，在期初到货。

假设8：前一天的期末库存等于后一天的期初库存。

假设9：本文考虑的库存优化问题为单阶段库存问题，不考虑商品物流存在多个运输节点。

2.3 目标函数

（1）持有成本和缺货成本

模型的目标函数中考虑到在计划周期内每一天存在的库存成本和缺货成本，其中库存和缺货成本根据该SKU的实际价格，按照其所属类别的持有成本系数和缺货成本系数得到。

（2）库存周转天数

模型的目标函数中考虑到整个计划周期内所有SKU的库存周转天数。

（3）订购成本

模型的目标函数中考虑到每个SKU在整个计划周期内存在的订购成本，具体的订购成本由该SKU的实际价格和所属类别的订购成本系数确定。

（4）目标函数

由于目标函数中存在不同的量纲，因此本文通过加权和的方式来设置模型的目标函数。

2.4 约束条件

（1）期初库存约束

期初库存约束主要对所有SKU在整个计划周期刚开始的库存容量水平进行约束。

（2）商品缺货量约束

商品缺货量约束主要对所有SKU在整个计划周期内每一天的缺货量进行约束，由于假设前三天没有补货量到达，因此该约束的表达形式存在两种。

（3）库存更新约束

库存更新约束主要对所有SKU在整个计划周期内每一天的库存平衡进行约束，由于假设前三天没有补货量到达，因此该约束的表达形式存在两种。约束［10］是为了保证前一天的期末库存等于后一天的期初库存。

（4）商品采购约束

商品采购约束主要对所有SKU在整个计划周期内每一天的采购量进行约束，如果当天的期末库存低于安全策略（s，S），即订购补货量至S。

（5）仓库容量约束

仓库容量约束主要指对每一个仓库的容量进行约束，针对每一个仓库中所有SKU每一天的补货量进行约束。

3 线性化处理

（1）商品缺货约束线性化处理

由于约束［6］和约束［7］存在逻辑约束，需要对其进行线性化处理，引入辅助0-1变量后约束如下：

（2）库存更新约束线性化处理

由于约束［8］和约束［9］存在逻辑约束，同样需要对其进行线性化处理，因其判断逻辑和商品缺货约束相同，因此同样使用辅助变量，线性化处理后如下：

（3）商品采购约束线性化处理

由于约束［11］存在逻辑约束，需要对其进行线性化处理，引入0-1辅助变量ipk，p，w，t，线性化处理结果如下：

4 改进遗传算法设计

本文提出改进遗传算法，对编码方式、交叉机制和变异机制进行了创新，提出的编码方式根据问题的属性进行构造。交叉机制是根据每一个SKU单品进行交叉，变异机制是对每一个SKU的安全库存进行变异，并生成一个新的序列。算法流程如图1所示。

4.1 编码方式和初始解生成

本文提出一种基于库存优化的全新编码方式，根据每一个SKU单品，前两位为安全库存策略s和S，接下来15个数字为每天的具体补货量。每一个SKU单品对应长度为17的列表，如果存在K个SKU单品，那么最后每个个体长度为17*K。

在初始解生成阶段，算法对历史需求信息进行分析，得到一些启发式信息，并将其运用在每个SKU单品安全库存设置部分，其中s为该单品15天内的平均需求量加上一个随机数，S为该单品15天内前三个最大需求量的总和。在对补货量x进行初始化时，算法设置每天补货量均为0，之后随机对其中某天的补货量进行增加，直到总补货量大于或等于需求量为止。

4.2 基于单品的交叉机制

在我们的遗传算法设计中，针对编码结构的特殊性，采取了创新的交叉操作策略。由于每个单品在编码中占据17个单位长度，交叉操作设计为围绕单个单品进行。具体来说，算法在执行交叉操作时，会选取以单品为单位的整体编码段进行交换，而非单个编码元素。这种方法的主要优势在于能够保障每个单品编码的完整性，确保交叉后的个体中每个单品所对应的编码仍然完整地反映其安全库存和补货量信息。这种精细化的交叉策略，不仅增强了遗传算法在维持编码结构一致性方面的能力，而且提高了算法在解空间探索中的效率和有效性，确保每次交叉操作都能产生有意义且可行的新个体，从而在遗传算法的整个演化过程中持续优化解决方案质量。

4.3 基于安全库存的变异机制

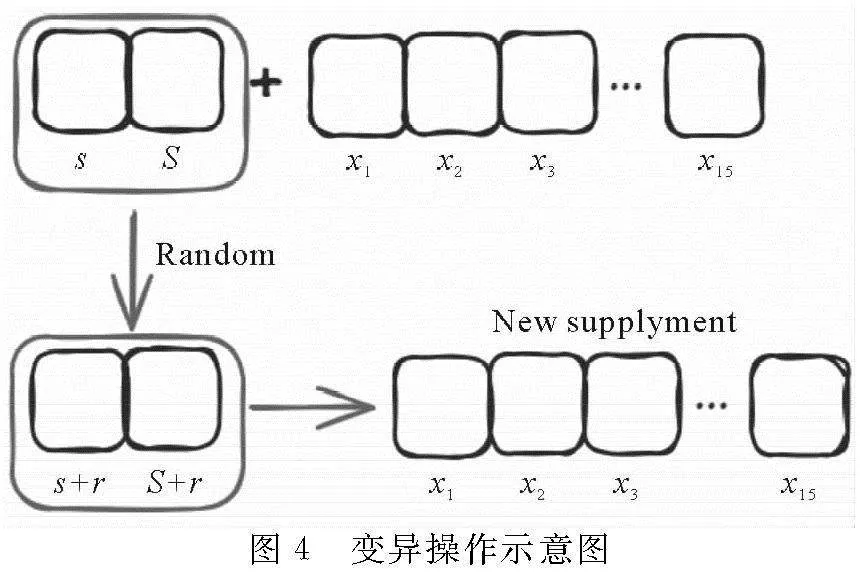
算法设计当中，考虑到编码方式的完整性，本文在对每一个体进行变异时，首先考虑安全库存s和S，通过增加一个随机扰动进行变异，之后根据变异的s和S对补货量数据再次进行初始化，完成对其中某个SKU单品的变异操作，每次变异过程中会挑选若干个单品进行变异，操作示意如图4所示。

4.4 选择机制

算法的选择机制根据每个个体的适应度值对种群进行更新，本文采用经典的轮盘赌机制和敬意保留机制。在每次选择过程中，保留适应度值最好的N个个体，对剩余的其他个体进行轮盘赌机制选择，对整个种群进行更新。

4.5 适应度值计算

考虑到库存优化问题的特殊性，同时考虑持有成本、订购成本和库存周转天数，通过每一个SKU个体的s、S和补货量个数，得到对应每一天的期初库存和期末库存，之后根据得到的具体库存数量计算对应的适应值，库存周转天数公式如下：

5 算例分析

5.1 算例设置

在算例设置过程中挑选四种类别，25个SKU单品，对100个单品进行库存优化决策，对每一天的补货量和计划周期T内的安全库存策略进行决策。对于模型中的具体参数部分，NRT盘点库存时间设置为1；LT订货提前期设置为3；库存持有成本和缺货成本根据当前SKU价格进行判断，库存持有成本为价格的40%，缺货成本为价格的60%；每个SKU每次的订购成本为商品售价的80%。具体的参数信息见表4。

5.2 算法求解和数值分析

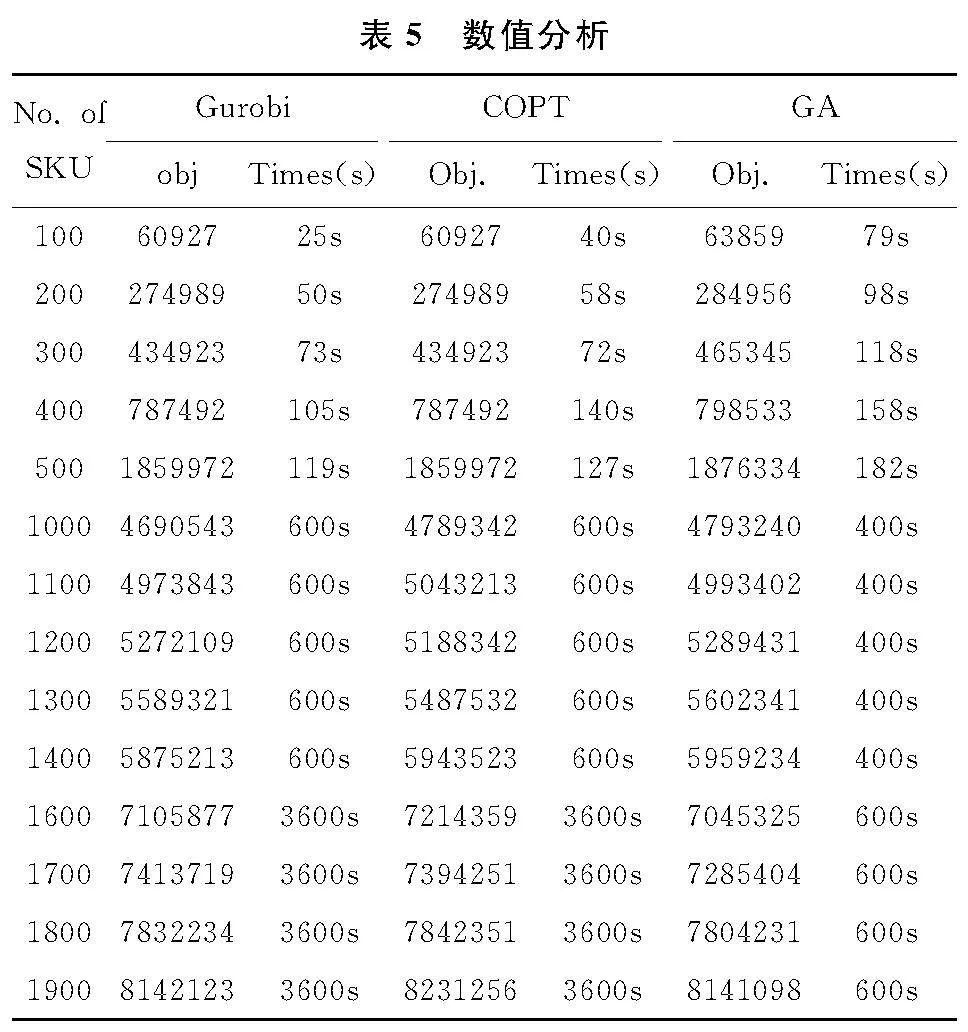
在本节中对三种不同求解方法的结果进行了细致的比较与分析，涵盖了Gurobi、COPT和遗传算法（GA）。这一比较主要集中在各方法求解问题的时间效率和结果精度两个关键方面。具体的数值结果已在表5中详细列出。从小规模算例的求解结果来看，Gurobi和COPT在精度和耗时上均明显优于GA，其中Gurobi求解速度最快。然而，在面对大规模算例的求解挑战时，传统求解器在运算过程中往往难以快速获得优质解决方案。相较之下，GA在这一场景下展现出了卓越的性能，不仅求解效率更高，而且能更快地接近最优解，显示出其在处理复杂大规模问题上的明显优势。

5.3 持有成本系数对不同价格商品库存优化模型的影响

本节主要对基于商品价格分类的库存优化模型进行灵敏度分析，对缺货成本和持有成本两个参数进行调整，得到其对模型的影响程度。

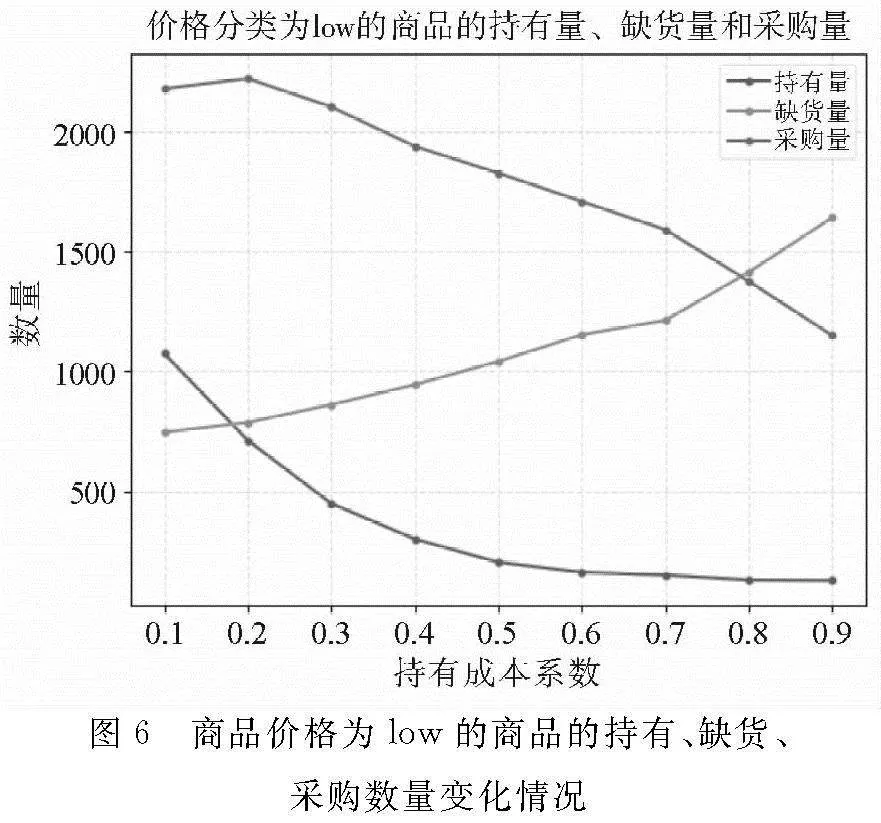
图5展示了不同价格分类的商品持有、缺货成本和所有商品的成本变化情况，可以看到无论商品价格高低，随着持有成本系数的增加（缺货成本系数的降低），四种类别的商品持有和缺货成本总是呈现先下降再上升的趋势，且均在商品的持有成本系数等于0.4时，该类别的持有缺货成本达到最低水平。当持有成本系数等于0.1、缺货成本等于0.9时，该类别的商品持有缺货成本总是低于持有成本系数等于0.9、缺货成本等于0.1时。该系数下该类别商品的库存数量和缺货数量见图6，持有成本越高、缺货成本越低，商品库存数量越少、缺货数量越多，且随着持有成本的增加，持有数量的下降速度从快逐渐到慢，缺货数量上升速度从慢变快，整体上商品的采购数量呈现下降的趋势，且下降速度逐渐加快。结合图7看到四种价格类型的商品随着持有成本系数的增加，采购成本均呈现出下降的趋势，且在本问中采购成本与采购次数相关，也就是说采购次数同样呈现出明显下降的趋势，下降的速度加快。对于价格高昂的商品，在持有成本高的情况下，采购数量和次数下降速度高于其他价格类型的商品。总之，当持有成本等于或大于缺货成本时，应当尽可能降低库存，当持有成本明显低于缺货成本时适合进行补货，价格更高的商品相比价格低的商品订购次数更少，尤其是在库存成本高的情况下。

图8绘制了不同价格分类的商品在不同持有成本系数下商品平均库存周转天数的变化情况，可以看到随着持有成本系数的增加，所有价格类型商品的库存周转天数都呈现出下降的趋势，尽管价格类型为high的商品在持有成本系数为0.6时出现向上的波动。只有当持有成本系数刚开始增加时，商品的库存周转天数显著降低，后期当持有成本增加时，库存周转天数的下降速度减慢，且逐渐稳定。同图5至图7，只有当商品持有成本特别低时，才适合进行补货和备货，否则应当尽可能降低库存。根据图8，价格类型为low的商品的库存周转天数高于其他价格类型的商品，也就是说价格越低的商品越适合执行囤货策略。

图9展示了四种价格类型商品的平均服务水平在不同持有成本系数下的变化情况。在持有成本较低的情况下，最优补货计划对于价格为veryhigh的商品的服务水平在0.8以上，高于另外三种类型。随着持有成本系数的增加，所有类型商品的服务水平都呈现出下降趋势，且下降速度加快，且通常价格为high和veryhigh的商品的服务水平高于low、medium类型。也就是说价格较高的商品应当尽可能避免缺货情况，其持有水平应当高于其他价格类型的商品，即使在持有成本较高的情况下。

5.4 订购成本系数对库存优化模型的影响

图 10绘制了不同订购成本系数下，补货计划的持有、缺货、订购成本的变化情况。从图10可以看出：随着订货成本系数的增加，总体捕获成本呈现上升的趋势，但是商品的持有成本保持相对稳定的趋势，在60000左右上下小幅浮动，商品的缺货成本则随着订购成本系数的增加展现出缓慢上升的趋势：当订货成本系数增加时，商品的订购总次数明显减少，但商品订购次数下降的速度从快变慢。结合图11可以看到，商品的总采购量也呈现出下降的趋势，持有量的上升幅度较小，缺货量的上升幅度相比持有量较大。订货成本较高的情况下，最优采购量下降，每次采购应当少量增加采购量，允许接受缺货的存在以降低库存总成本。

根据图10可以看到尽管随着订购成本系数的增加，库存周转天数呈现下降的趋势，但分布在0.8～0.9，下降幅度较小，相比持有成本系数的变化对库存的影响较小。该下降可能是由缺货造成的，由于订购成本增加，商家可以牺牲缺货成本，保持缺货状态，控制库存周转天数，从而降低成本。

5.5 最大库存水平S和最小库存水平s对补货计划的影响

本文建立的模型假设是基于周期内的s、S为同一值不产生变化，同时本文也对比了当每天的s、S都处于变动的情况下，如果订购成本等于0，最优的补货策略是当天的订购量为提前期后的需求量，此时每天的期末水平IE均等于0，见图 12，此时商品的总持有和库存成本等于0。对比图13，当s、S在库存周期内保持不变时，其订购量不随需求变动，而是同时受到持有成本、库存成本的影响。也就是说，最优的补货策略应当严格遵守需求值，此时能够带来最小的持有缺货成本和库存周转天数，且满足较高的商品服务水平。

6 结论

随着大数据和人工智能技术的发展，越来越多的研究开始聚焦于运用先进的数据分析和优化技术来解决库存优化问题。例如，机器学习方法在需求预测中显示出巨大的潜力，能够处理和分析大量的历史数据，从而提高预测的准确性。此外，优化算法如混合整数规划、启发式算法等，已被广泛应用于库存管理策略优化，以适应电商环境的动态变化和复杂性。

对于库存优化问题，本文构建数学模型，以安全库存策略s、S和每日的补货量为核心决策变量，目标为最小化库存总持有成本、库存周转天数和订购成本。对模型非线性部分进行了线性化处理，并使用Gurobi和COPT进行求解验证。最后，本文将改进的遗传算法应用于库存优化问题，提出了一种全新的编码方式，并根据问题特点设置了定制的交叉和变异策略，数值实验证明了该算法在求解库存优化问题上的有效性。但本文主要聚焦于确定性情况的讨论，后续会结合随机性进行研究。

参考文献：

［1］ 孙月，邱若臻.联合订货下基于Φ-散度的多产品库存鲁棒优化模型［J］.运筹与管理，2020，29（6）：97-106.

［2］ 温兆琦. OAO模式下F跨境电商企业的爆品库存优化研究［D］.厦门：厦门大学，2019.

［3］ ACIMOVIC J， GRAVES S C. Mitigating spillover in online retailing via replenishment［J］.M&som-manufacturing & Service Operations Management，2017，19（3）： 419-436.

［4］ HE S M， SETHURAMAN J， WANG X. A noncooperative approach to cost allocation in joint replenishment［J］. Operations Research，2017，65（6）：1562-1573.

［5］ PROTOPAPPA-SICKE M， SICKE M A， THONEMANN U W. Optimal two-period inventory allocation under multiple service level contracts［J］. European Joumal of Operational Research，2016，252（1）：145-155.

［6］ PADILTA T S V， CREEMERS S， BOUTE R N. Collaborative shipping under different cost-sharing agreements［J］. European Journal of Operational Rescarch， 2017，263（3）：827-837.

［7］ STENIUS O， KARAARSLAN A G， MARKLUND. Exact analysis of divergent inventory systems with time-based shipment consolidation and compound poisson demand［J］.Operation Research，2016，64（4）：906-921.

［8］ 王林，郑贵莲，曾宇容.考虑资源约束和数量折扣的联合补货-选址库存协同优化研究［J］.运筹与管理，2019，28（1）：17-26.

［9］ 宋世强.市域农产品电商冷链补货周期模型研究［J］.商讯，2018（2）：59-61.

［10］ 艾学轶，张金隆，徐浩轩，等.考虑保存技术投资的非立即变质品定价和库存联合决策［J］.系统管理学报，2020（1）：150-157.

［11］ 成诚，左传，王宜举.带短期价格折扣和允许两次特殊补货的库存决策模型［J］.运筹学学报，2018，22（2）：139-156.

［12］ 董琪，徐廷学，丛林虎.基于Markov三级库存系统备件横向调拨配置模型［J］.系统工程与电子技术，2015，37（11）：2524-2530.

［13］ 曹斌斌，孙静春，赵媛.考虑补货策略的供需驱动链牛鞭效应分析［J］.系统工程，2015，33（11）：38-45.