基于GARCH-GA-BP模型的股市波动率预测研究

【摘 要】波动率是衡量金融资产收益不确定性的重要指标，由于真实的波动率无法直接观测，因此构建合理的波动率模型来估计真实波动率显得尤为重要。论文对沪深300指数收益率的波动率进行GARCH建模，并在此基础上构建了基于GARCH-GA-BP的波动率混合预测模型。实证结果表明，相对于GARCH-BP模型和GARCH-SVR模型，论文提出的基于遗传算法优化的GARCH-GA-BP模型能显著提高股市波动率的预测精度。

【关键词】GARCH模型；GA算法；BP模型；波动率

【中图分类号】F832.5 【文献标志码】A   【文章编号】1673-1069（2024）07-0124-03

1 引言

GARCH模型因其阐明了标的资产收益率波动的主要特征，在金融市场风险评估领域的应用最为广泛。但是GARCH模型对数据的平稳性和正态性有一定的前提要求并且容易出现过拟合的情况。近年来，随着科学技术的加速发展，已有部分学者将机器学习方法应用于波动率的预测中。邱冬阳等[1]对上海黄金期货高频数据进行预测，发现改进的EN-LSTM模型可以提升短期波动率的预测精度。Christensen et al.[2]运用机器学习方法预测道琼斯工业平均指数成分股的波动率，研究发现3种机器学习算法（正则化、回归树和神经网络）均优于HAR模型。Kyoung-Sook和Hongjoong[3]基于LSTM深度学习方法提出了一种预测股市波动率的算法，并采用2010-2016年的标准普尔500指数等5个股票市场指数的数据对算法进行了检验。Zhang et al.[4]应用机器学习模型预测股票市场每日实际波动率，结果表明神经网络模型在性能方面最优。Liu和Fu[5]利用灰色模型和极限学习机（ELM）的混合算法来预测IBOR的波动率，结果发现与BP和经典ELM的预测结果相比，新模型对IBOR中短期波动率的预测效率更高。但是将机器学习算法和GARCH模型相结合的研究较少，尤其是在股票市场的波动率预测方面。如刘晨旸[6]通过构建SVR-GARCH模型对货币价格波动率进行预测，发现其提高了原有GARCH模型的预测精度。Koo和Kim[7]采用VU-GARCH-LSTM的组合模型对标准普尔500指数的实际波动率进行预测，结果表明该混合模型的预测效果优于LSTM-GARCH。因此本文将GARCH模型捕获的股票市场波动性等特征信息融入BP模型的底层，并利用遗传算法对BP神经网络进行优化，提出了一种基于遗传算法优化的BP模型与GARCH模型相结合的混合模型来预测股票市场的波动率，以期提高股市收益率波动的预测精度。

2 理论基础

2.1 GARCH模型

2.2 BP神经网络模型

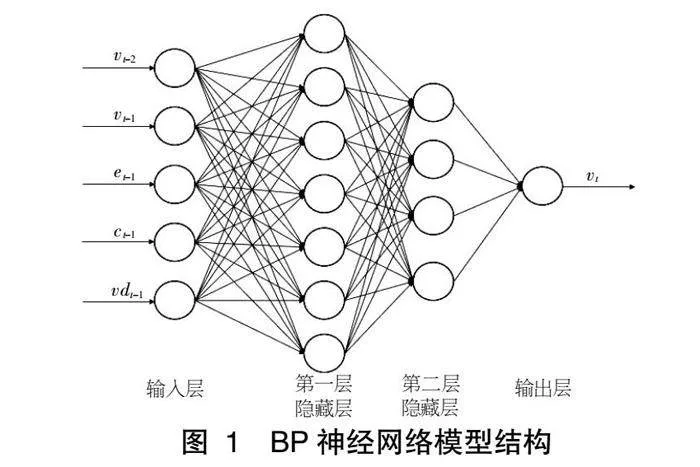
BP神经网络模型[9]是一种误差反向传播的多层前馈神经网络，是目前神经网络模型中最具代表性且应用最普遍的模型，主要包括输入层、隐藏层、输出层。本文将预测前两天的波动率vt-2，vt-1，前一天的极差et-1、收盘价ct-1、成交量volt-1共5个指标作为神经网络的输入，当天的波动率vt为输出，其结构如图1所示。

2.3 GA-BP模型

遗传算法是一种基于自然选择和基因遗传学原理的随机并行搜索算法。由于BP神经网络存在随机选取初始权值和阈值的缺点，而GA算法能够优化其初始权值、阈值，使BP神经网络未成熟收敛得以改善，非线性映射能力得到充分发挥，且保留遗传算法收敛速度快、学习能力强的优良性能。GA-BP模型[10]的主要过程如下：

第一，根据训练集和测试集确定神经网络结构。

第二，编码。

第三，确定适应度函数。

式中，SE为期望输出值与实际输出值之间的误差平方之和。

第四，初始化种群并依照步骤三中的公式计算适应度函数。

第五，根据适应度进行选择、交叉、变异。

第六，循环步骤三至五，直至达到训练目标或最大迭代次数为止。

第七，训练神经网络，得到最优解。

2.4 GARCH-GA-BP模型

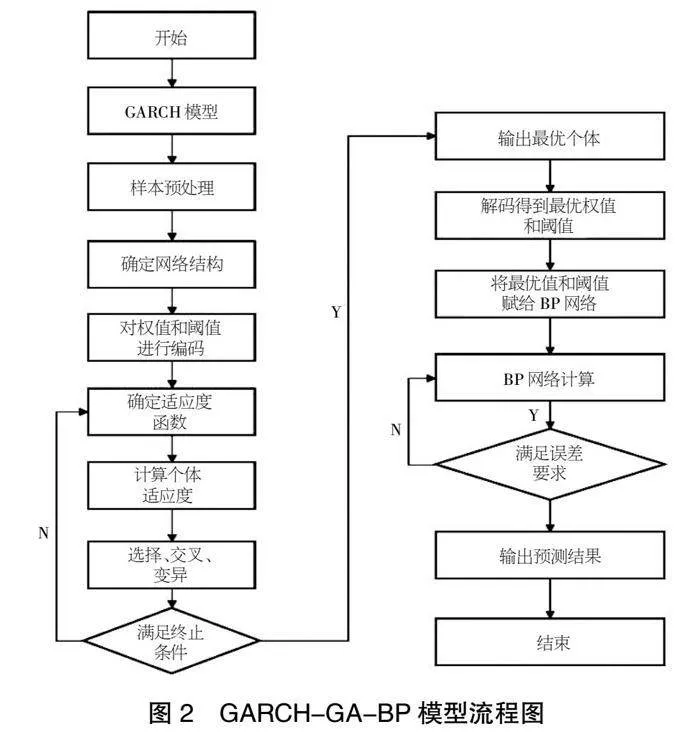
本文结合GARCH模型和GA-BP模型的优点，构建了GARCH-GA-BP模型，即将GARCH模型的预测值作为BP神经网络的输入值，并通过GA算法对BP神经网络进行参数调优获得最优解。算法的流程如图2所示。

3 实证分析

3.1 数据描述性统计

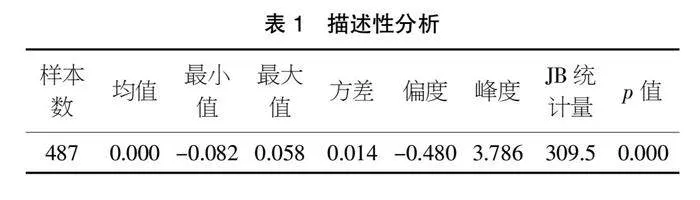
本文以2018/6/13～2020/6/13沪深300指数收益率为研究对象，表1为其对数收益率的描述性分析。结果显示，对数收益率的均值为0，峰度为3.786，且p值为0，因此拒绝该数据服从正态分布的假设。

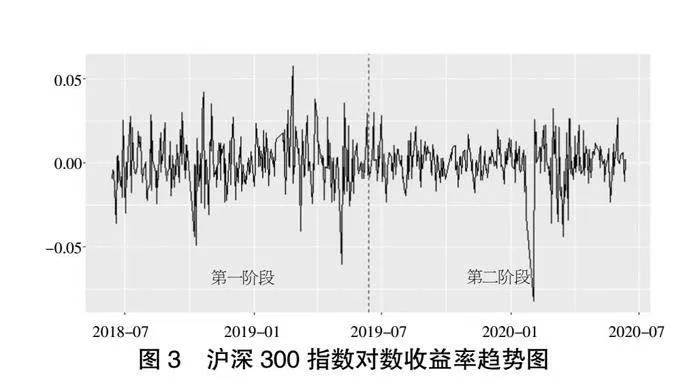
图3为沪深300指数对数收益率趋势图，从图3可以看出对数收益率存在明显的波动聚集性，说明该序列存在异方差性。

3.2 数据统计分析

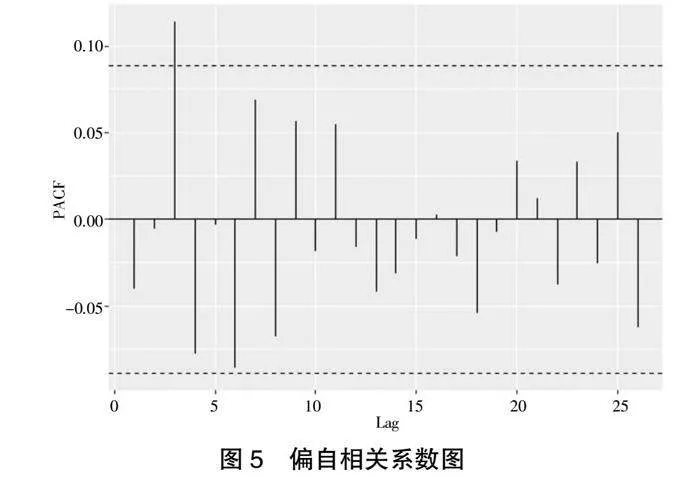
图4与图5分别是该指数对数收益率的自相关与偏自相关图，可以看出该序列与滞后三阶数据间存在较小的序列相关性。同时，本文利用最小AIC准则判断，当建立ARIMA（0，0，0）时，模型的AIC最小，为-2 769.83。结合表1中沪深300指数对数收益率均值为0，本文直接建立GARCH模型，不再需要对原始序列建立均值方程。

表2为ADF平稳性检验结果，从表2结果可以看出该指数对数收益率是平稳序列，因此可以建立GARCH模型。

LM检验判断序列是否存在ARCH效应，结果如表3所示。从表3中看出p值为0.121 4，在显著性水平为0.1的水平下不能拒绝原假设，即原对数收益率序列存在ARCH效应。

3.3 GARCH（1，1）模型结果

考虑沪深300指数对数收益率并不服从正态分布，本文利用极大似然法估计对数收益率序列服从自由度约为4的t分布。因此，在建立GARCH模型时，本文假设序列收益率服从自由度为4的t分布。GARCH模型的系数如表4所示。

为检验GARCH（1，1）模型的有效性，本文对该模型的残差进行了Ljung-Box白噪声检验与ARCH效应检验。Ljung-Box白噪声检验的p值为0.901 6，说明残差符合白噪声；ARCH效应检验中的p值为0.01，说明残差不存在ARCH效应。因此，本文建立的GARCH（1，1）模型是合理的。

3.4 波动率预测与评估

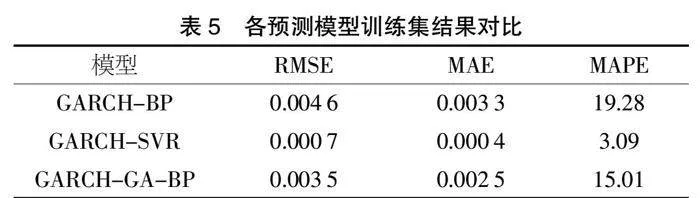
本文将样本集划分为训练集与测试集，采用滚动时间窗口的方法进行预测。其中训练集为2018/6/13～2020/1/15的388个样本，测试集为2020/1/16～2020/6/13的97个样本。选取收盘价及其极差、成交量、滞后一阶及二阶波动率共5个指标作为模型输入，当期波动率作为输出建立模型。通过计算各模型RMSE、MAE及MAPE来比较各模型的预测性能。各指标计算公式如下：

型。为了使本文提出的模型更具有说服力，本文同时加入了支持向量回归（SVR）模型进行结果对比。模型在训练集与测试集的表现结果分别如表5与表6所示。

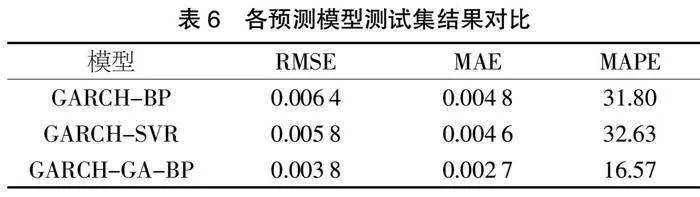
从表5与表6的结果可以看出，GARCH-SVR模型在训练集的各指标是所有模型中最小的一个，而测试集的指标要明显高于训练集，可见GARCH-SVR模型容易造成过拟合现象。而本文提出的GARCH-GA-BP在训练集与测试集均表现出了更好的结果，说明了将GA方法应用到神经网络参数的优化过程中，可以很好地解决传统神经网络容易达到局部最优解的问题，并提高了模型的预测精度。

4 结论

波动率在风险管理、衍生品定价和对冲、投资组合选择等金融领域都扮演着重要的角色。随着全球金融市场一体化，对波动率模型的精度要求也在不断提高，因此构建合理的模型来捕捉金融资产收益率的波动，度量金融市场的风险，对投资者和监管部门都具有重要的理论和实践意义。本文以沪深300指数收益率作为研究对象，提出了基于遗传算法优化的GARCH-GA-BP波动率预测模型，结果发现：基于遗传算法优化的GARCH-GA-BP模型的预测精度明显优于GARCH-BP模型和GARCH-SVR模型，且与GARCH-BP模型相比，测试集上的RMSEBsJwZL0wURKscI8YZ3Ukhg==、MAE及MAPE值分别降低了40.63%、43.75%和47.89%。

【参考文献】

【1】邱冬阳，丁玲，何一夫.基于高频数据和EN-LSTM的黄金期货短期波动率预测[J].运筹与管理，2024，33（03）：184-190.

【2】Christensen K， Mathias S， Bezirgen V. A machine learning approach to volatility forecasting[J].Journal of Financial Econometrics，2023，21（5）：1680-1727.

【3】Kyoung-Sook M， Hongjoong K I M. Performance of deep learning in prediction of stock market volatility[J]. Economic Computation & Economic Cybernetics Studies & Research，2019，53（2）：77-92.

【4】Zhang C， Zhang Y， Cucuringu M， et al. Volatility forecasting with machine learning and intraday commonality[J]. Journal of Financial Econometrics，2024，22（2）：492-530.

【5】Liu X， Fu H. Volatility forecasting for interbank offered rate using grey extreme learning machine： The case of China[J]. Chaos， Solitons & Fractals， 2016（89）：249-254.

【6】刘晨旸.基于SVR-GARCH的货币波动率预测研究——以加密货币和传统货币为例[J].国际经贸探索，2023，39（01）：52-67.

【7】Koo E， Kim， G. A hybrid prediction model integrating garch models with a distribution manipulation strategy based on lstm networks for stock market volatility[J].IEEE Access，2022（10）：34743-34754.

【8】Bollerslev Tim. Generalized autoregressive conditional heteros-kedasticity[J]. North-Holland，1986，31（3）：307-327.

【9】崔文喆，李宝毅，于德胜.基于GARCH模型和BP神经网络模型的股票价格预测实证分析[J].天津师范大学学报（自然科版），2019，39（05）：30-34.

【10】薛倩男，高岳林.基于时间序列的GA-BP神经网络股价预测模型[J].兰州文理学院学报（自然科学版），2017，31（05）：46-49.