“猪脚模型”在初中数学平行线相关题目中的应用

【摘要】随着教育改革的深入，寻找更加生动、有趣的教学方法成为教育工作者关注的焦点.本文主要探讨一种新的教学方法——猪脚模型在初中数学平行线相关题目中的应用.首先介绍猪脚模型的定义和基本原理，使得学生能够更加直观地理解平行线之间的角度关系.然后通过具体的例子和练习，展示猪脚模型在实际解题中的应用，并分析其对学生学习兴趣和思维能力的影响.

【关键词】初中数学；平行线；猪脚模型

1 引言

如图1所示，若AB∥CD，则∠B+∠D=∠E.由于该图外形像“猪脚”，因此这一定理被称为“猪脚模型”.在初中数学的教学中，平行线的性质是一个重要的内容.在学习平行线的性质时，学生经常会遇到一些有关角度的问题.为了帮助学生更好地理解和解决这类问题，教师可以引入一个有趣且形象的模型——猪脚模型.通过运用猪脚模型，学生可以更加轻松地解决平行线相关题目.他们不再需要死记硬背公式，而是可以通过观察和思考来找到答案.这种教学方法的引入，不仅提高了学生的学习兴趣，也培养了他们的观察力和思维能力.

2 试题呈现

已知直线AB∥CD，点E、F分别在直线AB、CD上，点P是直线AB与CD外一点，连接PE、PF.

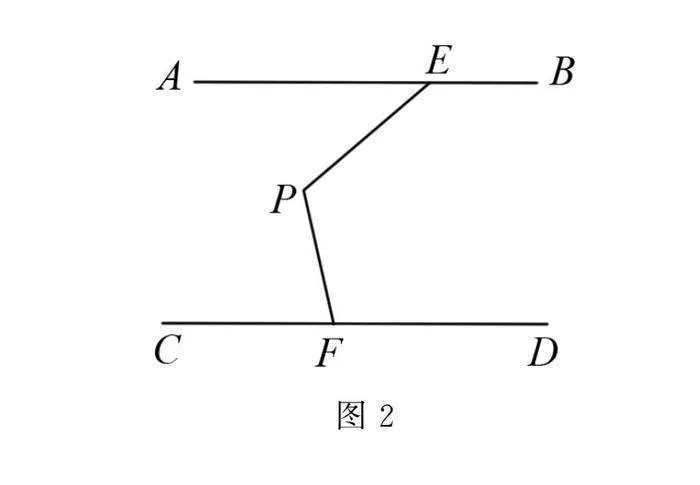
（1）如图2，若∠AEP=45°，∠DFP=105°，求∠EPF的度数；

（2）如图3，过点E作∠AEP的角平分线EM交FP的延长线于点M，∠DFP的角平分线FN交EM的反向延长线交于点N，若∠M与3∠N互补，试探索直线EP与直线FN的位置关系，并说明理由；

（3）若点P在直线AB的上方且不在直线EF上，作∠DFP的角平分线FN交∠AEP的角平分线EM所在直线于点N，请直接写出∠EPF与∠ENF的数量关系.

3 思路分析

第一问为“猪脚模型”的证明，过P作PQ∥AB，根据平行线的性质可得∠EPF=120°，在解题过程中，如不需详细步骤的题目，可直接应用；第二问根据角平分线的定义和三角形外角的性质可得结论；第三问根据角平分线的定义和平行线的性质分情况讨论即可.

4 解题探究

（1）如图4，过P作PQ∥AB，

因为AB∥CD，

所以PQ∥CD，

所以∠QPE=∠AEP=45°，∠QPF=∠180°－∠DFP=180°－105°=75°，

所以∠EPF=∠QPE+∠QPF=45°+75°=120°，该结论即为“猪脚模型”.

（2）EP∥FN，如图5，

因为EM平分∠AEP，FN平分∠MFD，

所以∠AEP=2∠1，∠MFD=2∠3，

由“猪脚模型”得，∠M=∠1+∠CFM=∠1+180°－2∠3=∠1+180°－2∠4，

所以AB∥CD，

所以∠3=∠4，

由三角形外角的性质可得，∠N=∠4－∠2=∠4－∠1，因为∠M与3∠N互补，

所以∠1+180°－2∠4+3（∠4－∠1）=180°，

整理得，∠4=2∠1=∠AEP，

所以EP∥FN.

第二问中用到第一问“猪脚模型”的结论，由于本题存在第一问，因此可以直接运用，当题目中没有第一问时，学生也应该锻炼运用“猪脚模型”的敏感性.

（3）①∠EPF+2∠ENF=180°.如图6，

因为AB∥CD，

所以∠CFH=∠EHF，∠EKF=∠DFK，

因为FN平分∠DFP，ME平分∠AEP，

所以∠CFH=180°－2∠DFK，∠AEP=2∠AEM=2∠KEN，由外角的性质得，∠EPF=∠EHF－∠AEP=180°－2∠DFK－2∠AEM，∠ENF=∠EKF+∠KEN=∠DFK+∠AEM，

所以∠EPF=180°－2∠ENF，

所以∠EPF+2∠ENF=180°.

②∠EPF=2∠ENF－180°，如图7，

因为AB∥CD，

所以∠PKB=∠PFD=2∠DFN，由外角的性质得，∠EPF=∠PKB－∠BEP=∠PKB－180°－2∠MEP=2∠DFN+2∠AEM－180°，

由“猪脚模型”得，∠ENF=∠DFN+∠NEK=∠DFN+∠AEM，

所以2∠ENF=2∠DFN+2∠AEM，

所以∠EPF=2∠ENF－180°.

5 结语

本题考查平行线判定和性质，角平分线的定义，三角形外角与内角的关系，根据题意理清各角之间的关系是解题关键.“猪脚模型”是平行线中的重要结论，需谨记其证明过程，并熟练运用.“猪脚模型”是一种有效的教学方法，它能够帮助学生更好地理解和解决初中数学中平行线相关题目.通过引入“猪脚模型”，学生能够更加直观地理解平行线之间的角度关系，提高他们的学习兴趣和思维能力.在教学过程中，教师可以通过举例和练习来引导学生运用“猪脚模型”.解决相关数学问题.使学生

更好地掌握平行线的性质.

参考文献：

［1］孙振飞，顾叶青.“平行线被折线所截问题”的探究：变式、开放、融合——兼谈沪教版初中数学教材中探究活动的教学［J］.数学教学，2023（12）：16-22.

［2］栾长伟.巧添平行线 构造相似形［J］.初中生学习指导，2023（33）：20-22.

［3］陈国权.平行线间的“拐点”问题［J］.中学教学参考，2023（23）：22-24.