永磁同步电机新型趋近律滑模控制器设计

摘 "要：针对传统指数趋近律中因函数不连续性所引起抖振和传统指数趋近律趋近速度与抖振抑制之间无法同时满足高性能控制系统要求的问题，提出基于系统状态变量的新型滑模趋近律并应用于永磁同步电机速度、电流控制器中。该趋近律通过引入系统状态变量幂次项和状态变量的双曲正弦值，使系统状态变量以等速和指数两种速率趋向切换面。这样可以加快系统到达切换面的速度，当系统接近切换面时，指数项接近于零，等速项开始起关键作用，对系统的抖振进行抑制。同时采用双曲正切开关函数替代符号函数，以去除因函数的不连续性所引起的抖振问题。该方法既能提高系统到达滑模面的速度，又能有效抑制固有抖振，提升系统的动态性能。仿真和实验结果表明，新型趋近律相比于传统指数趋近律能够有效降低永磁同步电机启动时转速超调，提高系统的响应速度、抑制系统的抖振。

关键词：永磁同步电机; 滑模控制; 速度控制器; 电流控制器；动态性能; 抖振问题

DOI：10.15938/j.emc.

中图分类号：TM341 " " " " " " 文献标志码：A " " " " "文章编号：1007-449X（2024）07-0000-00

Design of a new reaching law of sliding mode controller for "permanent magnet synchronous motor

KANG Erliang1， ZHU Jinrong1， HAN Kangwei2

（1. Engineering Technology Research Center of High Efficiency Direct-Drive System in Universities in Heilongjiang， Harbin University of Science and Technology， Harbin 150080， China; 2. Technical Center for Mechanical and Electrical Product Inspection and Testing of Shanghai Customs District， Shanghai 200030， China）

Abstract： In order to solve the problem that the jitter caused by the function discontinuity in the traditional exponential reaching law and the approaching speed and jitter suppression of the traditional exponential reaching law cannot meet the requirements of the high-performance control system at the same time， a new sliding mode reaching law based on system state variables was proposed and applied to the speed and current controller of permanent magnet synchronous motor. By introducing the power terms of the system state variable and the hyperbolic sine of the state variable， the system state variable tends to the sliding-mode surface at two rates： isokinetic and exponential. The speed at which the system reaches the sliding-mode surface can be accelerated by this method. And when the system approaches the sliding-mode surface， the exponential term approaches zero， and the isokinetic term begins to play a key role in suppressing the jitter of the system. At the same time， the hyperbolic tangent switch function is used instead of the symbolic function to eliminate the jitter problem caused by the discontinuity of the function. This method can not only improve the speed of the system reaching the sliding-mode surface， but also effectively suppress the inherent jitter and improve the dynamic performance of the system. Simulation and experimental results show that compared with the traditional exponential approach law， the new approach law can effectively reduce the speed overshoot of the permanent magnet synchronous motor when starting， improve the response speed of the system， and suppress the jitter of the system.

Keywords： permanent magnet synchronous motor; sliding mode control; speed controller; current controller; dynamic performance; jitter issues

0 引 "言

永磁同步电机（permanent magnet synchronous motor，PMSM）具有结构简单、功率密度高、效率高、调速性能好等优点，已广泛应用于新能源交通和发电、机器人、物流、航空航天、高精度伺服等热点领域[1-2]。传统的线性控制方法如比例积分控制因其结构简单被广泛应用于PMSM控制系统中，但PMSM是一个多变量、强耦合、非线性、参数可变的控制对象，传统线性控制方法无法满足高性能控制的要求[2-4]。

为了解决传统线性控制方法的问题，国内外学者提出并发展了一些非线性控制理论，如模糊控制[5]、自抗扰控制[6]、预测控制[7]、滑模控制（sliding mode control，SMC） [8-10]、神经网络控制[11]。其中，SMC由于其具有强鲁棒性以及对系统不确定性不敏感等优势被广泛应用于运动控制、过程控制等领域[12]。

但在实际应用中，传统SMC超调量大、响应速度慢、存在抖振等问题，阻碍了SMC在工业中的应用。为了克服上述问题，趋近律法[13]、高阶滑模法[14]、非奇异终端滑模法[15]、分数阶滑模法[16]等众多方法被提出。其中，趋近律法因为可以直接作用于趋近过程，所以可以更加有效地解决抖振问题。

文献[17]提出一种基于变速趋近律方法的 PMSM滑模速度控制策略，该方法可以改善系统的鲁棒性、提升系统的动态响应速度。文献[18]提出一种基于改进的幂次指数趋近律的模糊自适应滑模控制方法，该方法有效降低抖振，提升系统静、动态性能。文献[19]在指数趋近律指数项中引入滑动曲面函数的幂项，使得趋近律在趋近过程中可以用两种不同的形式表示，实验结果表明该方法可以有效抑制抖振。

为了进一步提高PMSM调速系统的动态性能，本文提出一种新型趋近律。新型趋近律通过引入状态变量的幂次项和双曲正弦值，使状态变量以等速和指数两种速率趋向切换面。这样可以加快系统到达切换面的速度，同时当系统接近切换面时，指数项接近于零，等速项开始起关键作用，对系统的抖振进行抑制。同时采用双曲正切开关函数替代符号函数，以去除因函数的不连续性所引起的抖振问题。

1.1 传统指数趋近律

传统指数趋近律公式为

（1）

式中sgn（s）函数在零点的不连续性会使控制系统产生时间和空间的滞后。此外，由于系统惯性和测量误差的存在会导致滑模运动轨迹在滑模切换面往返穿梭，从而产生抖振。

同时，当运动点到达滑模面时有 。通过对其从0到t进行积分可得运动点到达滑模面的时间为

（2）

从式（2）可以看出，指数系数 与到达时间 成反比。即若想系统快速到达滑模面就要使 值尽可能大；但 值过大，会导致系统在趋近于滑模面时速度较快，增大系统抖振。

由此可知，传统指数趋近律无法同时满足趋近速度与抖振抑制的要求，且仍然存在传统滑模因函数的不连续性所引起的抖振问题。

1.2 新型趋近律

根据上述问题，提出新型滑模趋近律为：

（3）

式中： ；x为系统的状态变量； 均为正数； 。

新型趋近律的指数项可以近似为：

（4）

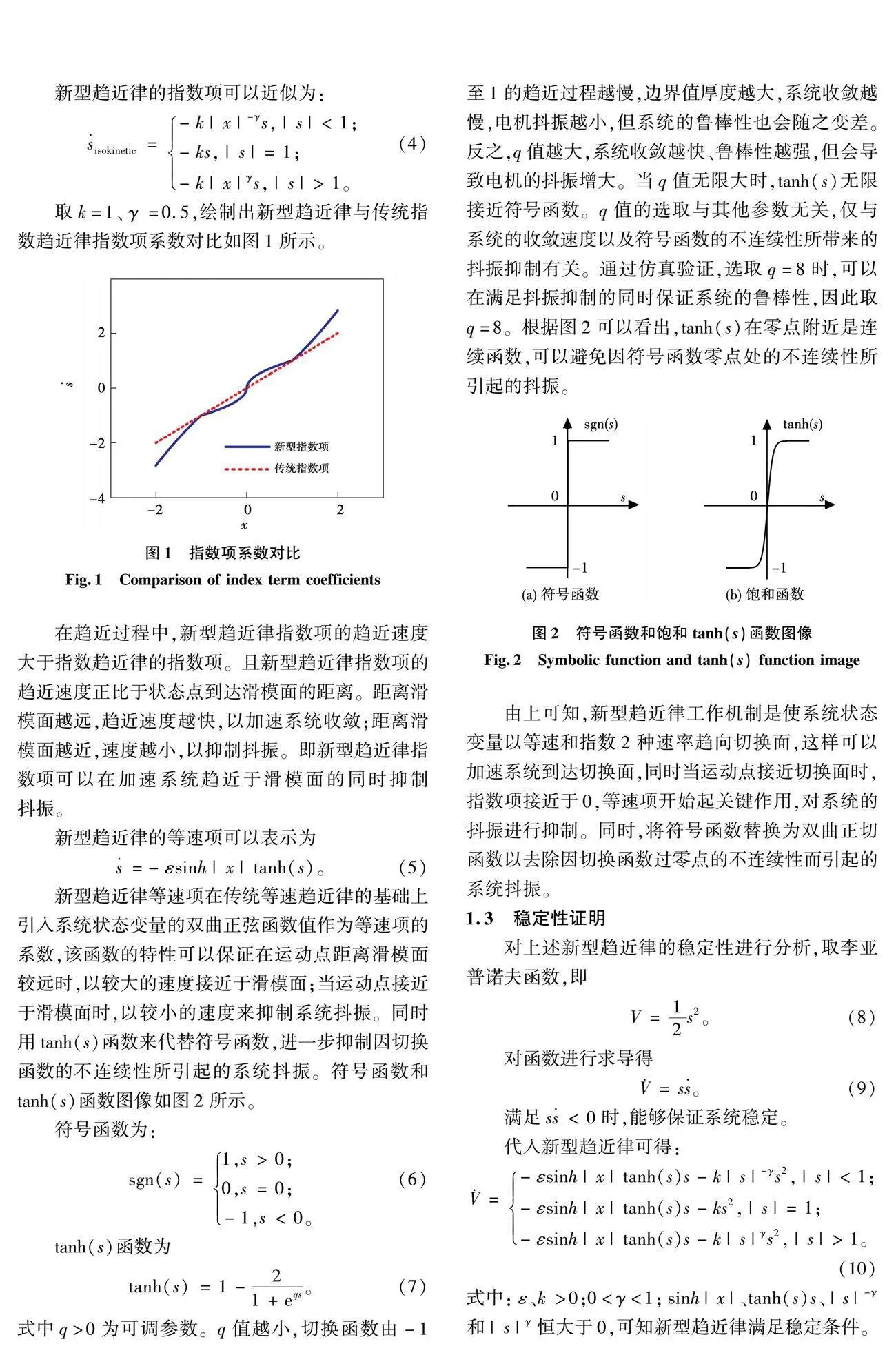
取k=1、 =0.5，绘制出新型趋近律与传统指数趋近律指数项系数对比如图1所示。

在趋近过程中，新型趋近律指数项的趋近速度大于指数趋近律的指数项。且新型趋近律指数项的趋近速度正比于状态点到达滑模面的距离。距离滑模面越远，趋近速度越快，以加速系统收敛；距离滑模面越近，速度越小，以抑制抖振。即新型趋近律指数项可以在加速系统趋近于滑模面的同时抑制抖振。

新型趋近律的等速项可以表示为

（5）

新型趋近律等速项在传统等速趋近律的基础上引入系统状态变量的双曲正弦函数值作为等速项的系数，该函数的特性可以保证在运动点距离滑模面较远时，以较大的速度接近于滑模面；当运动点接近于滑模面时，以较小的速度来抑制系统抖振。同时用tanh（s）函数来代替符号函数，进一步抑制因切换函数的不连续性所引起的系统抖振。符号函数和tanh（s）函数图像如图2所示。

符号函数公式为：

（6）

tanh（s）函数公式为

（7）

式中qgt;0为可调参数。q值越小，切换函数由-1至1的趋近过程越慢，边界值厚度越大，系统收敛越慢，电机抖振越小，但系统的鲁棒性也会随之变差。反之，q值越大，系统收敛越快、鲁棒性越强，但会导致电机的抖振增大。当q值无限大时，tanh（s）无限接近符号函数。q值的选取与其他参数无关，仅与系统的收敛速度以及符号函数的不连续性所带来抖振抑制有关。通过仿真验证，在选取q=8，可以在满足抖振抑制的同时保证系统的鲁棒性，因此取q=8。根据图2可以看出，tanh（s）在零点附近是连续函数可以避免因符号函数零点处的不连续性所引起的抖振。

由上可知，新型趋近律工作机制是使系统状态变量以等速和指数两种速率趋向切换面，这样可以加速系统到达切换面，同时当运动点接近切换面时，指数项接近于零，等速项开始起关键作用，对系统的抖振进行抑制。同时将符号函数替换为双曲正切函数以去除因切换函数过零点的不连续性而引起的系统抖振。

1.3 稳定性证明

对上述新型趋近律的稳定性进行分析，取李亚普诺夫函数，即

（8）

对函数进行求导得

（9）

满足 时，能够保证系统稳定。

代入新型趋近律可得：

（10）

式中： gt;0； ； 、 、 和 恒大于0，可知新型趋近律满足稳定性条件。

2 基于状态变量的新型趋近律滑模控制器设计

采用 控制策略。表贴式永磁同步电机 坐标系下的数学模型为：

（11）

定义PMSM控制系统的状态变量为：

（12）

式中： 为电机的参考转速； 为电机的实际转速。

定义 、 ，可得

（13）

定义滑模面函数为

（14）

式中 为待设计参数。

采用1.2节中设计的新型趋近律，对式（14）求导可得PMSM速度控制器的输出为

（15）

对式（15）进行积分运算，可得q轴的参考电流为

（16）

式（16）中积分项的引入可以进一步减小控制系统的抖振、降低系统的稳态误差，提高控制系统的性能。

2.2 滑模电流控制器设计

定义系统的状态变量为：

（17）

定义滑模面函数为：

（18）

坐标系下，表贴式PMSM解耦后的电流方程为：

（19）

联立式（18）、式（19）并将新型趋近律代入可得控制器的输出为：

（20）

3 仿真和实验验证

3.1 仿真结果分析

采用 控制方式，通过Simulink分别搭建基于传统滑模控制（traditional sliding mode control，TSMC）和新型滑模控制（new sliding mode control，NSMC）的仿真模型，以验证新型趋近律的可行性和有效性。永磁同步电机控制系统框图如图3所示。

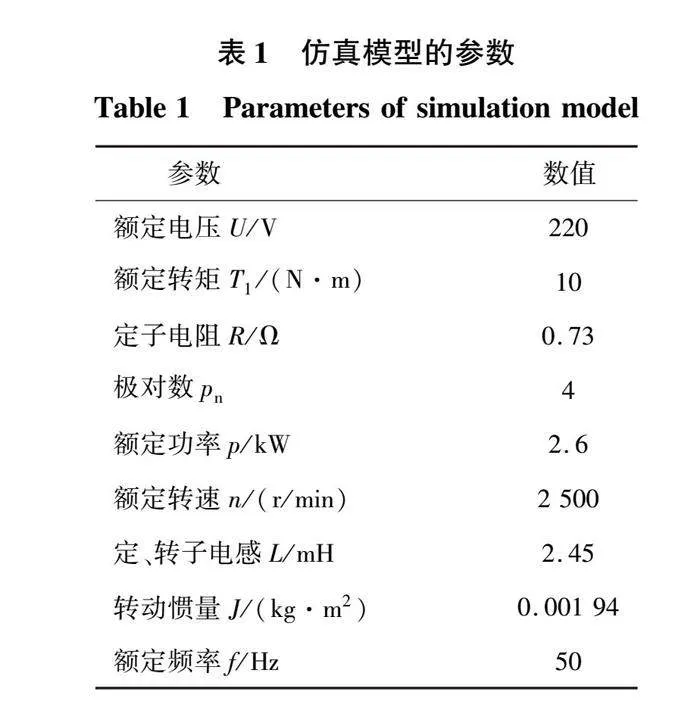
设定仿真时间为0.4s，给定转速为1000 。系统启动时带7 负载转矩，在0.2s时负载变为10 ，在0.3s时恢复为7 。永磁同步电机参数如表1所示。

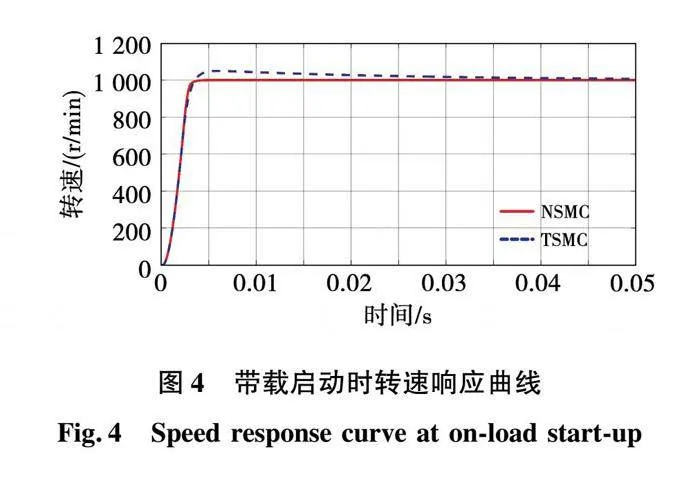
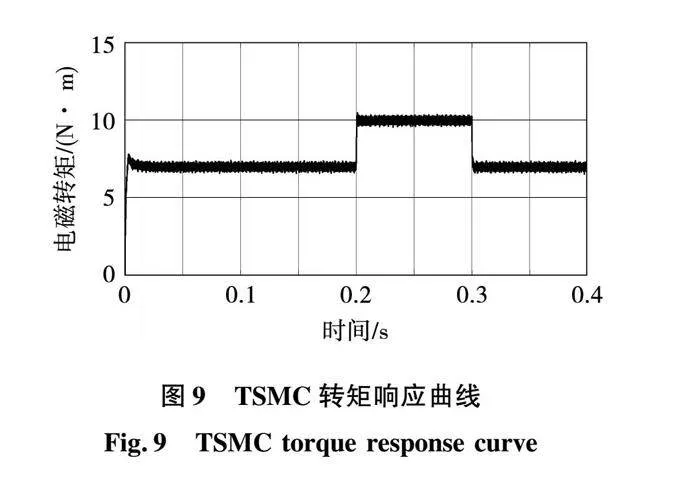
仿真结果如图4～图10所示。

电机启动时带7 负载转矩，由图4可知，指数趋近律控制下的转速超调量为4.5%，响应时间约为0.045s；新型趋近律控制下的转速超调量几乎为0，响应时间约为0.005s。

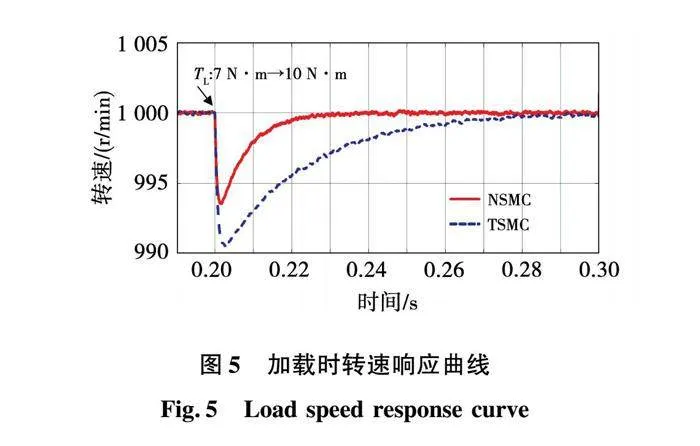
图5为系统加载时转速响应曲线，在0.2s时负载由7 变为10 ，指数趋近律控制下转速下降9.6 ，经过0.08s恢复到给定转速。新型趋近律控制下下降6.4 ，经过0.03s恢复到给定转速。

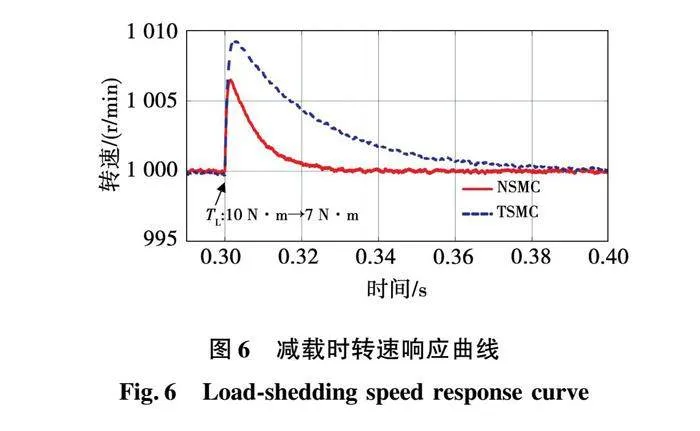
图6为系统减载时转速响应曲线，在0.3s时负载由10 恢复为7 ，指数趋近律控制下转速上升9.3 ，经过0.08s恢复到给定转速。新型趋近律控制下转速上升6.4 ，经过0.03s恢复到给定转速。

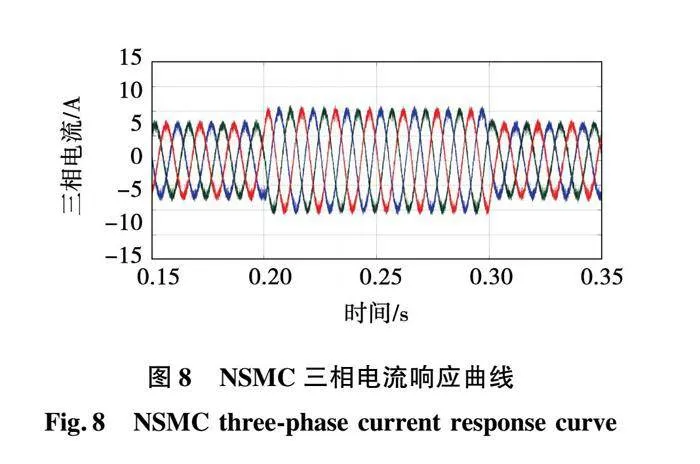
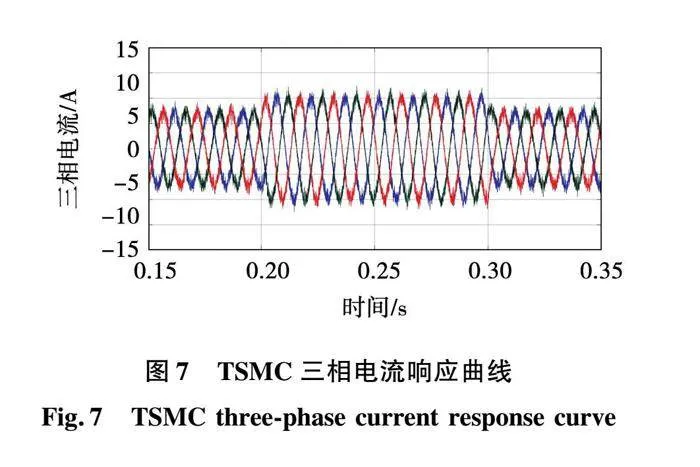
由图7和图8可知，指数趋近律控制下的三相电流毛刺较大，波形畸变明显，而新型趋近律控制下的三相电流更加平滑。

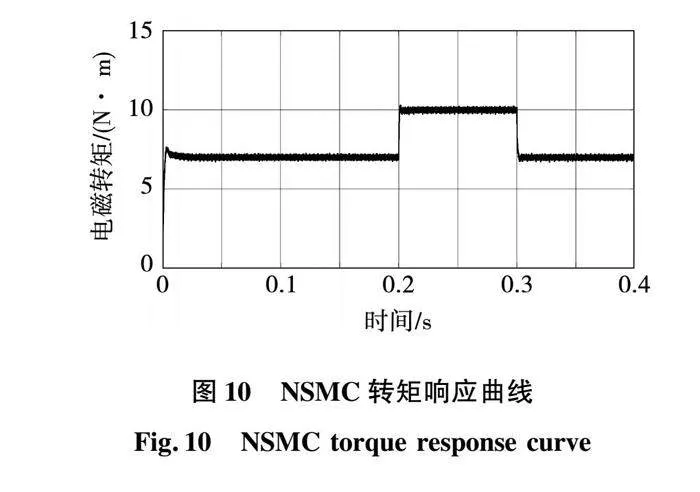
由图9和图10可知，指数趋近律控制下的电磁转矩在0.8 左右波动。新型趋近律控制下电磁转矩在0.5 左右波动。

图4～图6的仿真结果表明，新型滑模趋近律相比于传统滑模趋近律具有更好的启动性能，在具有更快的响应速度的同时可以实现无超调启动。同时系统的带载能力和抗扰性也有所提升。图7～图10的仿真结果表明，新型趋近律相比于指数趋近律可以有效抑制PMSM控制系统的抖振，提高控制精度。仿真结果验证了新型趋近律的有效性。

3.2 实验结果分析

为验证上文提出的新型趋近律在工程上的正确性与可行性，根据图3搭建PMSM控制系统实验平台如图11所示。控制核心采用TMS320F28335芯片，采用直流可调电源调节负载电机进而实现对电机施加不同的负载的效果，最后通过示波器观察实验结果。实验系统电机的参数同表1的电机参数一致。

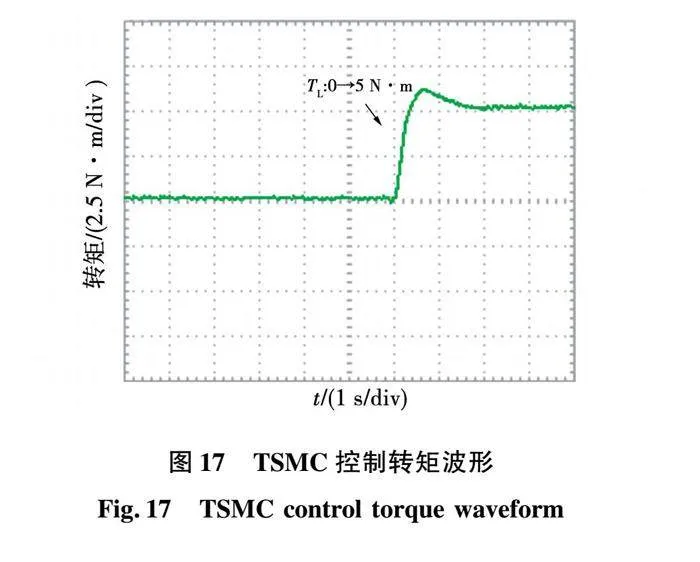
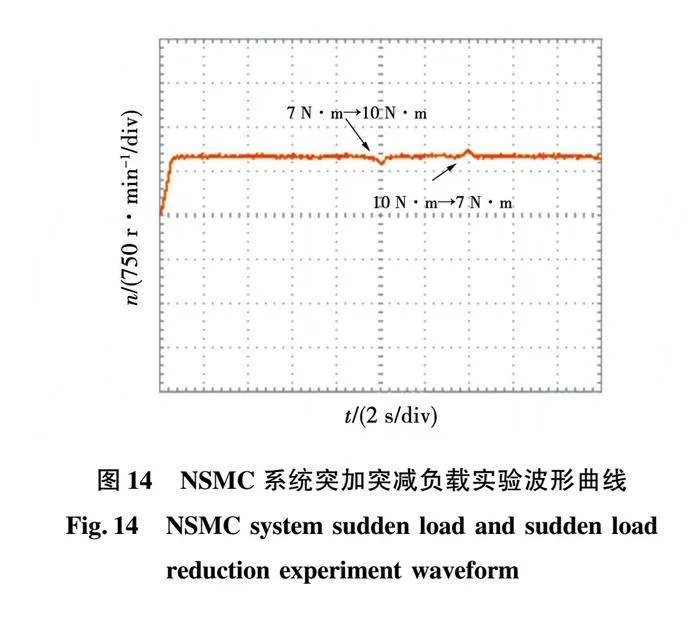
实验结果如图12～图20所示。

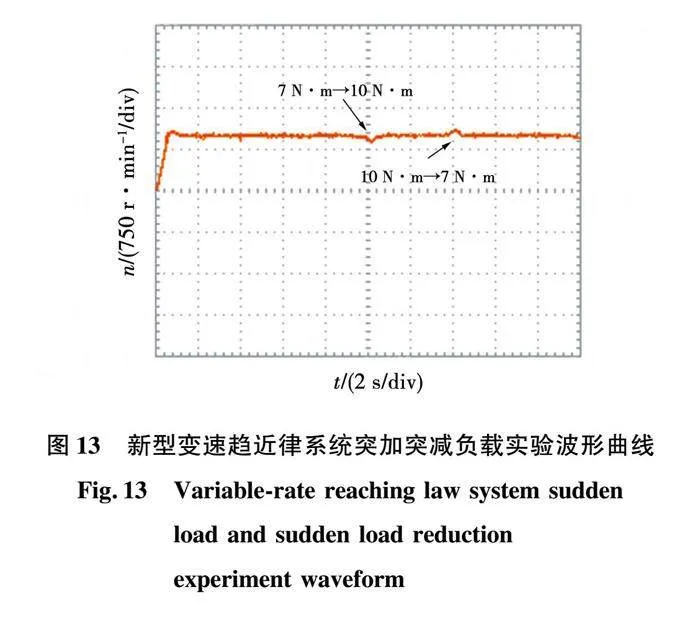
图13为文献[17]中所提新型变速趋近律在本实验平台相同实验条件下转速实验波形，在给定转速为1000 时，转速超调量为10%，调节时间为1.2s，系统加载时转速波动95 ，经过0.9s恢复至给定转速；系统减载时转速波动100 ，经过1s恢复至给定转速，可以验证所提趋近律应用于PMSM控制系统可对系统的动态性能有进一步提升。

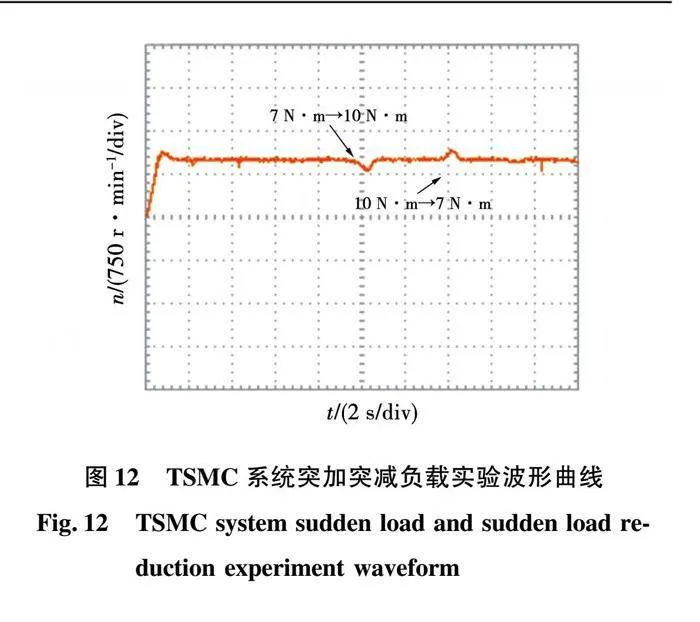
由图12、图14可以看出，在给定转速为1000 时，指数趋近律控制下转速超调量为12.5%，调节时间为1.2s，系统加载时转速波动200 ，经过1.6s恢复至给定转速；系统减载时转速波动170 ，经过1.4s恢复至给定转速。新型趋近律控制下转速超调量几乎为0，调节时间为0.8s，系统加载时转速下降130 ，经过1.2s恢复至给定转速；系统减载时转速上升120 ，经过0.8s恢复至给定转速。实验结果与仿真结果基本相同，验证了新型趋近律相比于指数趋近律具有更小的超调量、更快的响应速度和更强的抗扰性能。

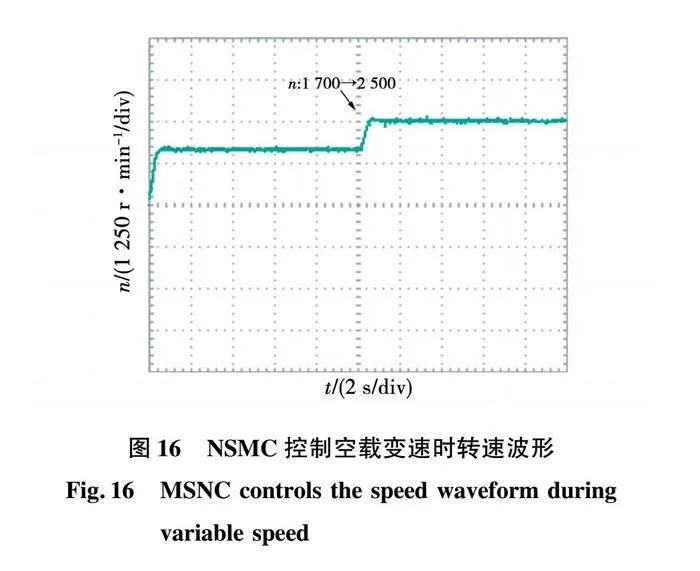
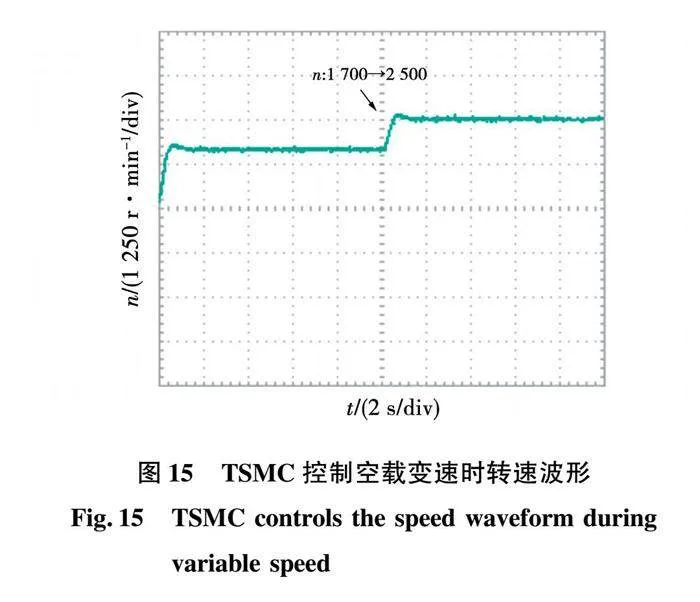
由图15、图16可知，指数趋近律在给定转速为1700 时超调量为10%，调节时间为1.2s；给定转速为2500 时超调量为4.4%，调节时间为1.6s。新型趋近律在给定转速为1700 超调量为1.7%调节时间为0.8s，在给定转速为2500 时超调量为2.4%，调节时间为0.7s。由此可知，新型趋近律应用于PMSM控制系统中具有更小的超调量、更快的调节时间。

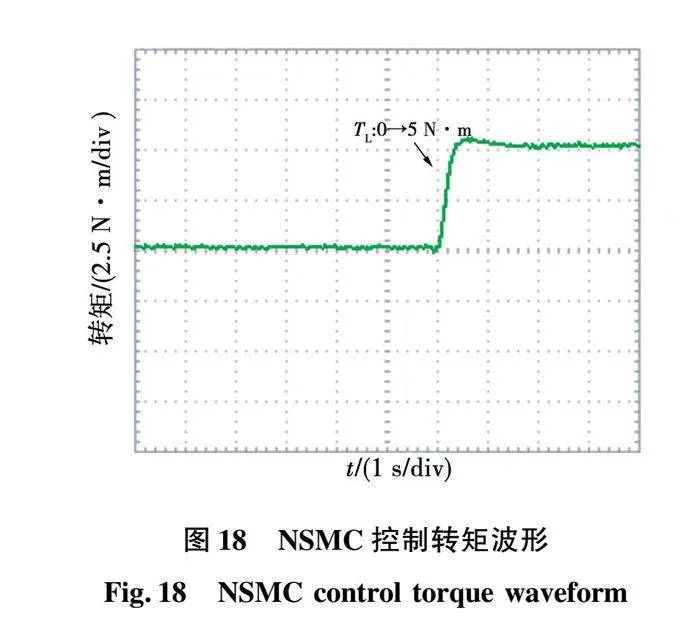
由图17、图18可知，在突加5 负载的情况下，新型趋近律相比于指数趋近律具有更快的动态响应能力。

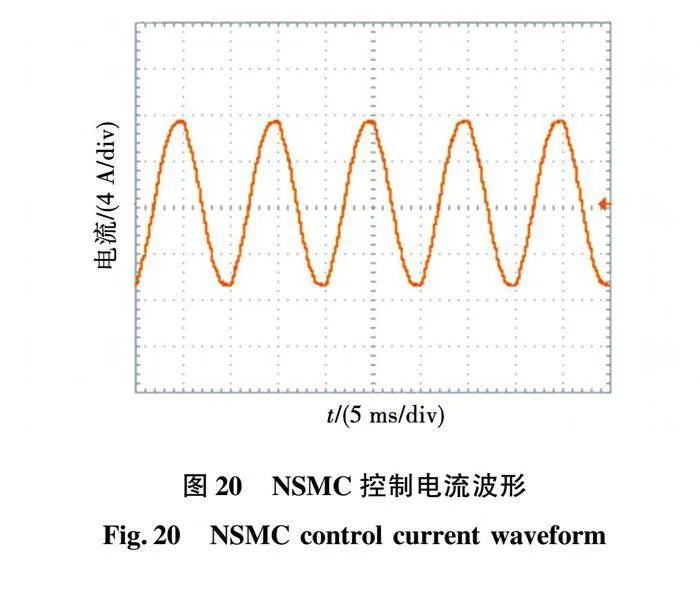
由图19和图20可知，指数趋近律控制下的电流毛刺较大，波形畸变明显，而新型趋近律控制下的电流更加平滑。

4 结 "论

本文针对传统滑模控制因切换函数不连续性的影响存在抖振和传统指数趋近律的趋近速度与抖振抑制之间无法同时满足高性能控制系统要求等问题，提出基于新型趋近律的滑模控制器。通过MATLAB/Simulink建立基于等速趋近律和新型趋近律的仿真模型，仿真结果表明，新型趋近律通过引入系统状态变量幂次项、状态变量双曲正弦值和采用双曲正切开关函数替代符号函数，可在加快PMSM控制系统的收敛速度、减小超调的同时抑制系统的抖振，提高系统的动态性能。最后，搭建PMSM调速系统实验平台，从工程上验证本文所提出的新型趋近律与传统等速趋近律相比，超调量更小、响应速度更快、抗扰性更强。

参 考 文 献：

[1] 陈卓易. 预测误差驱动的永磁同步电机有限集模型预测控制[D].杭州：浙江大学，2018.

[2] WU Shaobo， SU Xiuqin， WANG Kaidi. Time-dependent global nonsingular fixed-time terminal sliding mode control-based speed tracking of permanent magnet synchronous motor[J]. IEEE Access， 2020， 8：186408.

[3] GAO Peng， ZHANG Guangming， OUYANG Huimin， et al. An adaptive super twisting nonlinear fractional order PID sliding mode control of permanent magnet synchronous motor speed regulation system based on extended state observer[J]. IEEE Access，2020， 8：53498.

[4] 吕从鑫， 汪波， 陈静波，等. 永磁同步电机控制策略综述与展望[J]. 电气传动自动化， 2022， 44（4）：10.

LV Congxin， WANG Bo， CHEN Jing， et al. Review and prospect of control strategies for permanent magnet synchronous motors [J]. Electric Drive Automation， 2022， 44（4）：10.

[5] CHOI H H， YUN H M， KIM Y. Implementation of evolutionary fuzzy PID speed controller for PM synchronous motor[J]. IEEE Transactions on Industrial Informatics， 2013， 11（2）：540.

[6] 王晓远， 刘铭鑫， 陈学永，等. 电动汽车用PMSM带滤波补偿三阶滑模自抗扰控制[J]. 电机与控制学报， 2021，25（11）：25.

WANG Xiaobo， LIU Mingxin， CHEN Xueyong， et al. Third-order sliding mode active disturbance rejection control of PMSM with filter compensation for electric vehicle [J].Electric Machines and Control，2021，25（11）： 25.

[7] 魏佳丹， 徐家扬， 陶文杰，等. 变母线电压工况下开绕组PMSM单矢量模型预测转矩优化控制[J]. 中国电机工程学报，2022，42（2）：772.

WEI Jiadan， XU Jiayang， TAO Wenjie， et al. Optimization method of single vector model predictive torque control for open-winding PMSM in Variable DC Bus voltage condition[J]. Proceedings of the CSEE， 2022，42（2）：772.

[8] XU W， JUNEJO A K， LIU Y， et al. An efficient antidisturbance sliding-mode speed control method for PMSM drive systems[J]. IEEE Transactions on Power Electronics，2021， 36（6）：6879.

[9] 赵希梅，李德豪，金鸿雁.基于扰动观测器和改进自适应二阶快速终端滑模的PMLSM伺服系统控制[J].电机与控制学报，2024，28（4）：41.

ZHAO Ximei， LI Dehao， JIN Hongyan. PMLSM servo system control based on disturbance observer and improved adaptive second order fast terminal sliding mode [J]. Electric Machines and Control， 2024，28（4）：41.

[10] ZAIHIDEE F M， MEKHILEF S， MUBIN M. Application of fractional order sliding mode control for speed control of permanent magnet synchronous motor[J]. IEEE Access， 2019， 7：101765.

[11] 张世强. 某武器系统平行度校准装置的控制系统设计[D].哈尔滨：哈尔滨工业大学，2011.

[12] 张晓光，孙力，赵克. 基于负载转矩滑模观测的永磁同步电机滑模控制[J]. 中国电机工程学报，2012，32（3）： 111.

ZHANG Xiaoguang，SUN Li，ZHAO Ke. Sliding mode control of PMSM based on a novel load torque sliding mode observer[J]. Proceedings of the CSEE，2012， 32（3）： 111.

[13] 樊英，周晓飞，张向阳，等.基于新型趋近律和混合速度控制器的IPMSM调速系统滑模变结构控制[J].电工技术学报，2017，32（5）：9.

FAN Ying， ZHOU Xiaofei， ZHANG Xiangyang， et al. Sliding mode control of IPMSM system based on a new reaching law and a hybrid speed controller [J].Transactions of China Electrotechnical Society，2017，32（5）：9.

[14] 皇甫宜耿， LAGHROUCHE S， 刘卫国，等.高阶滑模消抖控制在永磁同步电动机中的应用[J].电机与控制学报，2012，16（2）：7.

HUANGFU Yigeng， LAGHROUCHE S， LIU Weiguo， et al. Chattering avoidance high order sliding mode control for permanent magnet synchronous motor[J].Electric Machines and Control，2012，16（2）：7.

[15] VAN M， MAVROVOUNIOTIS M， GE S S. An adaptive backstepping nonsingular fast terminal sliding mode control for robust fault tolerant control of robot manipulators[J]. IEEE Transactions on Systems， 2019， 49（7）： 1448.

[16] HUANG Jiacai， LI Hongsheng， CHEN Yangquan， et al. Robust position control of PMSM using fractional-order sliding mode controller[J]. Abstract and Applied Analysis，2012（4）：473.

[17] 李中琴. 基于新型变速趋近律的永磁同步电机滑模控制[J]. 电机与控制应用， 2017， 44（5）：5.

LI Zhongqin. Sliding mode control for permanent magnet synchronous motor based on variable-rate reaching law method [J]. Electric Machines amp; Control Application， 2017， 44（5）：5.

[18] 苗敬利， 郑大伟， 周重霞. 基于新型趋近律的永磁同步电机模糊滑模控制[J]. 电气传动， 2019（3）：5.

MIAO Jingli， ZHENG Dawei， ZHOU Chongxia. Fuzzy sliding mode control of permanent magnet synchronous motor based on a novel reaching law [J]. Electric Drive， 2019（3）：5.

[19] WANG Y， FENG Y， ZHANG X， et al. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system[J]. IEEE Transactions on Power Electronics， 2020， 35（4）：4117.

（编辑：邱赫男）