高频链矩阵变换器直接功率反步控制策略

摘 "要：针对高频链矩阵变换器（HFLMC）电路前后级耦合，导致系统动态性能和鲁棒性降低的问题，提出一种基于直接功率的非线性反步控制策略（nonlinear backstepping control strategy based on direct power，BS-DPC）。首先建立HFLMC非线性数学模型和有功、无功功率动态模型，分析双极性电流空间矢量调制策略；然后在考虑系统不确定性情况下引入2个解耦控制分量，设计直流输出电流和无功功率反步控制器，实现电池不同工况下输出电流参考值的快速跟踪控制。最后根据李雅普诺夫稳定性理论证明HFLMC闭环系统全局渐进稳定性，并对比传统PI直接功率控制和BS-DPC策略，仿真和实验结果表明，所提BS-DPC策略控制HFLMC提高了输出电流的动态性能和电网波动及直流滤波电感变化下的鲁棒性，响应时间减少了约78%，网侧THD降低了0.98%。

关键词：高频链矩阵变换器；双极性电流空间矢量调制；PI直接功率控制；直接功率反步控制；动态响应；鲁棒性

DOI：10.15938/j.emc.

中图分类号：TM461 " " " " " " " " " " " " " " " " " " " " " 文献标志码：A " " " " " " " " " " " " " " " " " "文章编号：1007-449X（2024）07-0000-00

Direct power backstepping control strategy for

high frequency chain matrix converter

WEI Yewen1， 2， BAI Wenjing1， LI Ming1

（1.College of Electrical Engineering amp; New Energy， China Three Gorges University， Yichang 443002， China;

2.Hubei Provincial Engineering Research Center of Intelligent Energy Technology， Yichang 443002， China）

Abstract：A nonlinear backstepping control strategy based on direct power （BS-DPC） is proposed to solve the problem that the dynamic performance and robustness of the system are reduced due to the coupling of the high-frequency link matrix converter （HFLMC） circuit. The nonlinear mathematical model of HFLMC and the dynamic model of active and reactive power are established， and the bipolar current space vector modulation strategy is analyzed. At the same time， considering the uncertainty of the system， two decoupling control components are introduced， and the DC output current and reactive power backstepping controller are designed to realize the fast tracking control of the output current reference value under different working conditions of the battery. According to the Lyapunov stability theory， the global asymptotic stability of the HFLMC closed-loop system is proved. Compared with the traditional PI direct power control and BS-DPC strategy， the simulation and experimental results show that the proposed BS-DPC strategy control HFLMC improves the dynamic performance of the output current and the robustness under grid fluctuation and DC filter inductance change. The proposed control strategy reduces the dynamic response time of the system by approximately 78%. The THD reduction on the grid side is 0.98% with the proposed control strategy.

Keywords： high-frequency link matrix converter; bipolar current space vector pulse width modulation; PI direct power control; direct power backstepping control; dynamic response; robustness

0 引 "言

电动汽车快速充电桩是为电池提供能量的必要设备，是电动汽车推广和应用的关键基础设施。随着新能源与电网的整合，研究满足V2G等高性能储能技术的双向变换器成为该问题的关键[1-2]。

传统电动汽车充电桩由两级拓扑结构组成，前级通常是功率因数校正（power factor correction，PFC）电路结构，后级为DC-DC隔离变换器，两级拓扑具有控制简单的优点[3]。然而，直流链路薄膜电容器增加了系统体积，降低了功率密度和可靠性。因此，无直流链电容的高频链矩阵变换器（high-frequency link matrix converter，HFLMC）以其高效、体积紧凑、可靠性高、寿命长和宽范围输出电压的优点，成为电动汽车充电器的首选[4]。

HFLMC的调制策略较为复杂，是保证电路运行的关键和难点。文献[5]提出一种对称双线电压调制法，全部开关器件可实现零电压开关（zero-voltage switch，ZVS）；文献[6]提出一种基于三移相的双周期解耦空间矢量相移调制来解耦变压器电流，以消除网侧电流总谐波失真。文献[7]提出双极性电流空间矢量调制策略（bipolar current space vector modulation，BC-SVM），降低了调制复杂度。上述调制方法中，BC-SVM策略因其网侧谐波失真率低、直流电压利用率高以及易于实现数字控制器而被广泛应用。

HFLMC作为一种单级电路拓扑，其交流侧连接电网，要求实现单位功率因数控制和低谐波等并网需求；对于电池侧，要求控制策略实现快速动态响应和强鲁棒性。传统的比例积分（proportional integral，PI）控制策略[8]，在跟踪同步坐标系下的控制变量参考值时存在稳态误差。文献[9]提出一种基于直接功率的无差拍预测控制策略，建立了无差拍参考电流矢量预测模型，具有对系统参数扰动不敏感的优点，但其动态响应时间长，跟踪性能差；文献[10]提出一种自适应滑模虚拟磁链观测器，并将其与传统的PI功率控制器相结合，以实现PWM整流器的无电压传感器直接功率控制，然而，他们对参数变化和外部扰动很敏感，并且滑模控制系统的中间变量可能会导致抖振问题。文献[11]提出一种双闭环反步控制（dual closed-loop backstepping control，DCL-BSC）策略，该策略由直流输出电流外环控制器和电网电流内环控制器组成，实现了稳定状态下的电流跟踪性能和瞬态下快速无超调响应的特性。

上述控制方法中，非线性反步控制（backstepping control，BSC）将复杂非线性系统分解成不超过系统阶数的低阶子系统，并逐一对每个子系统设计Lyapunov函数和中间虚拟控制量，确保跟踪误差收敛为零，输出快速准确地跟踪参考值，整个系统及各个反步阶段渐近稳定，最终完成整个控制律的设计[12]。BSC策略已广泛应用于航空航天系统[13-15]和电机驱动[16-17]等领域，并具有优越的控制性能。此外，BSC在功率转换系统中的应用也不断涌现。文献[18]中针对孤岛直流微电网中的不同部件设计了非线性自适应BSC策略，保证了直流微电网的稳定性。文献[19]提出了用于燃料电池堆/升压功率转换器系统自适应BSC方案，实现了输出电压的精确调节和较强的鲁棒性。文献[20]为三相PWM整流器的直接功率控制设计了一种反步控制（BSC）方法，该方法实现了良好的输入/输出性能，并能够抑制系统参数的不确定性。

基于以上分析，本研究针对HFLMC，提出一种基于直接功率的非线性反步双闭环控制（nonlinear backstepping control strategy based on direct power，BS-DPC）策略，设计了一个内环有功和无功功率回路和一个外环直流侧输出电流回路，通过调节瞬时无功功率实现了单位功率因数，所提控制策略为HFLMC提供了更好的动态性能、强鲁棒性和低谐波失真率，并考虑了系统参数的不确定性。

1 HFLMC的数学及动态模型

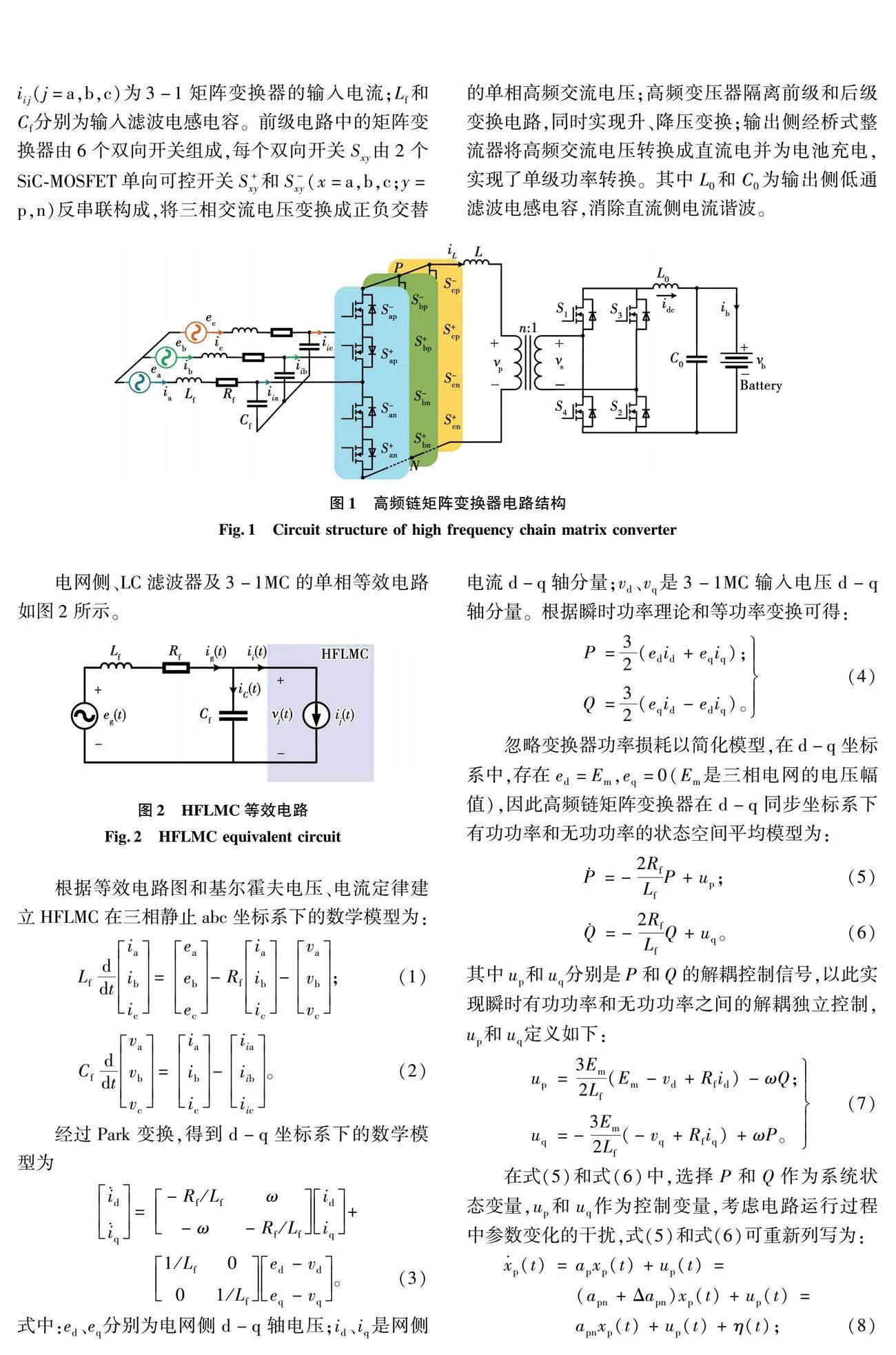
HFLMC电路拓扑结构如图1所示。整个系统由三相输入滤波器、3-1矩阵变换器、高频变压器及输出侧不可控桥式整流器、输出滤波器组成。其中：ei和ii（i=a，b，c）为电网侧输入电压和电流；iij（j=a，b，c）为3-1矩阵变换器的输入电流；Lf和Cf分别为输入滤波电感电容。前级电路中的矩阵变换器由6个双向开关组成，每个双向开关Sxy由2个SiC-MOSFET单向可控开关S+ xy和S- xy（x=a，b，c；y=p，n）反串联构成，将三相交流电压变换成正负交替的单相高频交流电压；高频变压器隔离前级和后级变换电路，同时实现升、降压变换；输出侧经桥式整流器将高频交流电压转换成直流电并为电池充电，实现了单级功率转换。其中L0和C0为输出侧低通滤波电感电容，消除直流侧电流谐波。

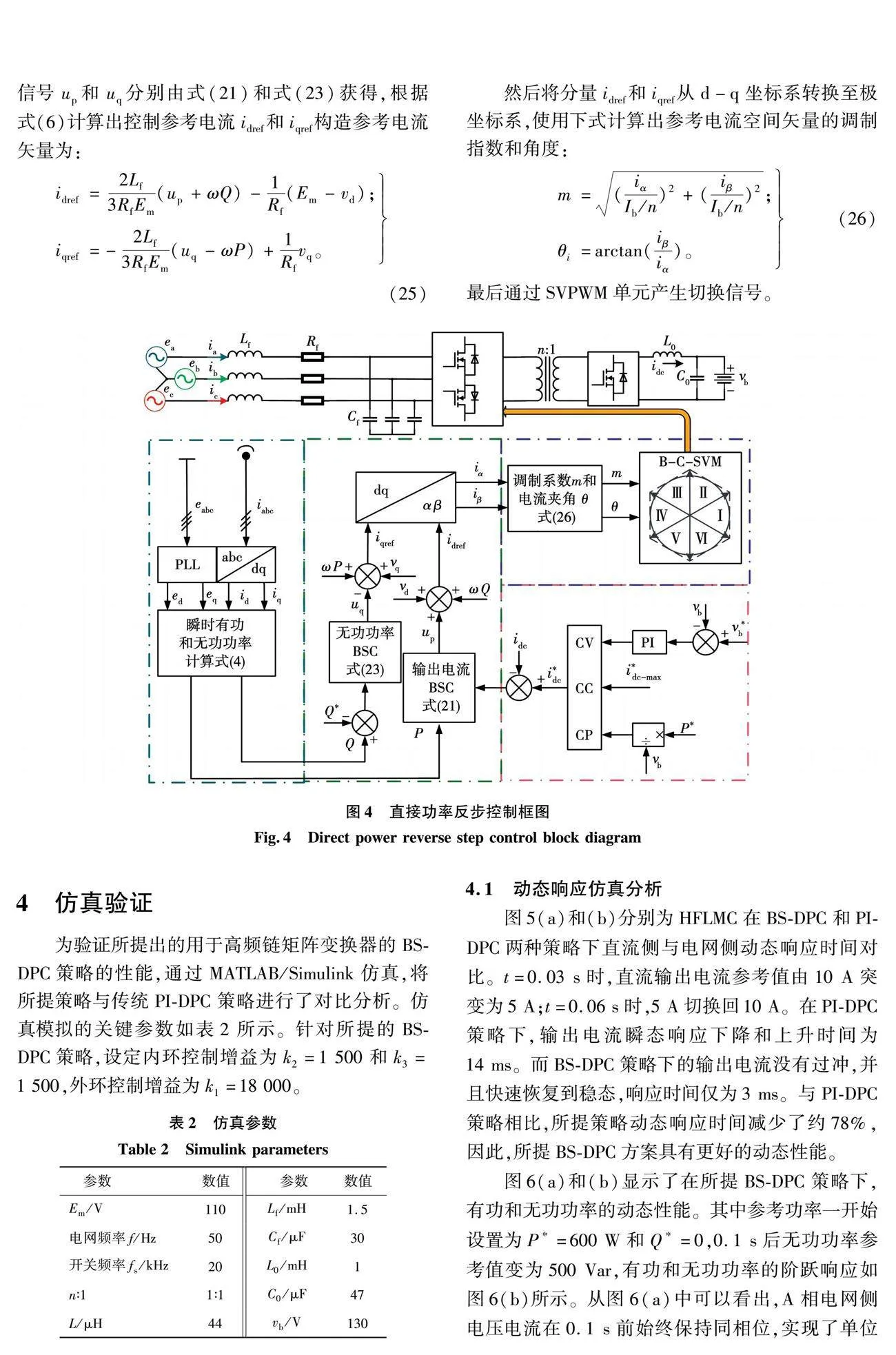
（26）

最后通过SVPWM单元产生切换信号。

2 仿真验证

为验证所提出的用于高频链矩阵变换器的BS-DPC策略的性能，通过MATLAB/Simulink仿真，将所提策略与传统PI-DPC策略进行了对比分析。仿真模拟的关键参数如表2所示。针对所提的BS-DPC策略，设定内环控制增益为 和 ，外环控制增益为 。

4.1 "动态响应仿真分析

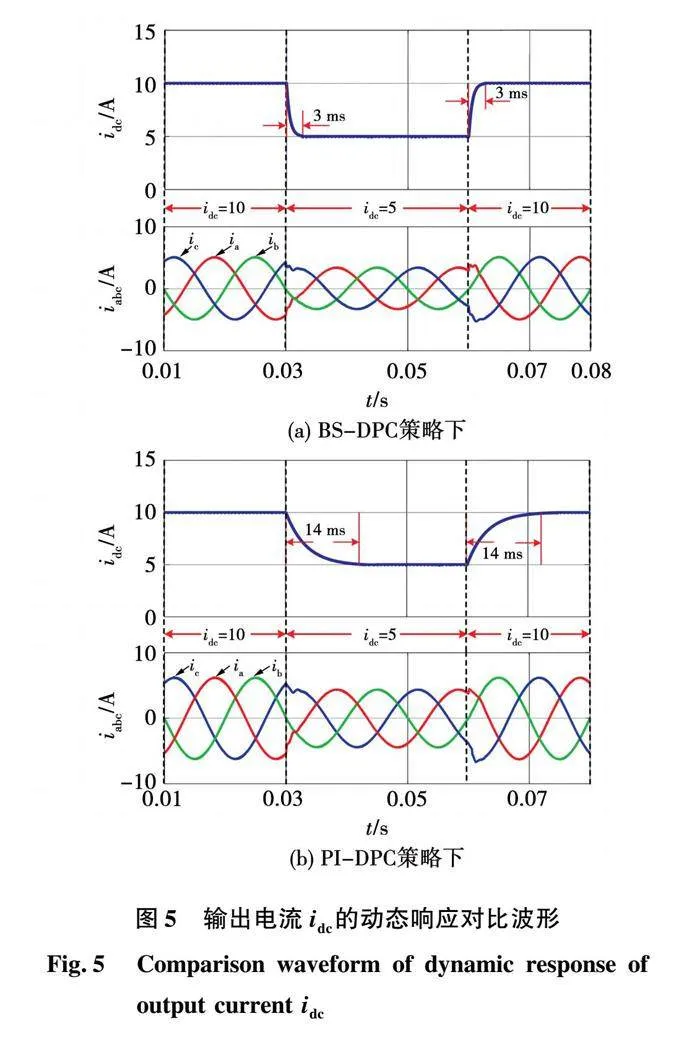
图5（a）和（b）分别为HFLMC在BS-DPC和PI-DPC两种策略下直流侧与电网侧动态响应时间对比。 时，直流输出电流参考值由10 A突变为5 A； 时，5 A切换回10 A。在PI-DPC策略下，输出电流瞬态响应下降和上升时间为14 ms。而BS-DPC策略下的输出电流没有过冲，并且快速恢复到稳态，响应时间仅为3 ms。与PI-DPC策略相比，所提策略动态响应时间减少了约78%，因此，所提BS-DPC方案具有更好的动态性能。

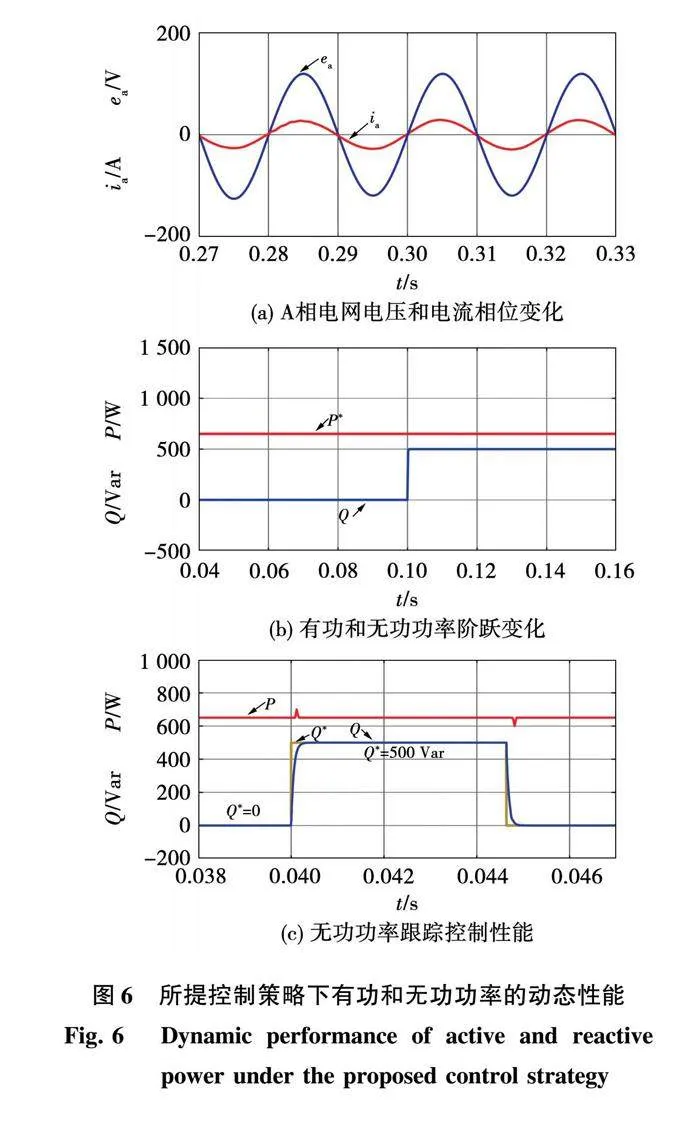
图6（a）和（b）显示了在所提BS-DPC策略下，有功和无功功率的动态性能。其中参考功率一开始设置为 W和 ，0.1 s后无功功率参考值变为500 Var，有功和无功功率的阶跃响应如图6（b）所示。从图6（a）中可以看出，A相电网侧电压电流在0.1 s前始终保持同相位，实现了单位功率因数，0.1 s后由于无功功率的突变，电流滞后于电压。为更清晰展示无功功率的跟踪控制性能，图6（c）设置无功功率在0.04 s时由0突变至500 Var，再由500 Var突变回0，无功功率2次动态响应时间均小于0.5 ms；无功功率跟踪动态过程中，有功功率对无功功率的阶跃变化几乎不敏感，因此所提BS-DPC策略可实现有功和无功功率的解耦控制。

4.2 "鲁棒性仿真分析

为验证所提控制策略的鲁棒性，在仿真中建立了2种扰动情况。案例1：输出电流参考值 A，将输出滤波电感值由1 mH切换至1.5 mH；案例2：A相相电压由初始值110 V，在 时下降5%。

BS-DPC策略及PI-DPC策略下电池测电流波形分别如图7（a）、（b）所示。由于输出电感的突变，在PI-DPC策略下idc的波动为5 A，并且11 ms后恢复至初始值；相比之下，BS-DPC策略下的idc在4 ms内达到稳态，响应时间约为传统策略的36.4%，输出电流波动幅值约为传统策略的60%。

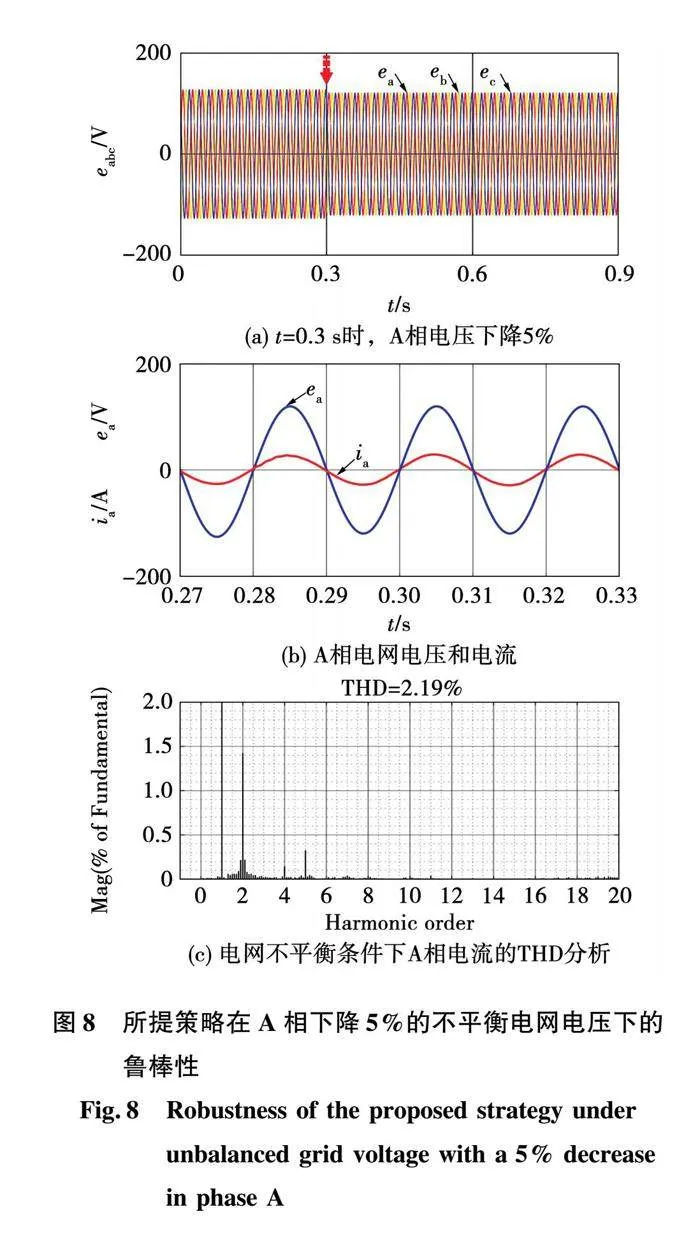
BS-DPC策略在不平衡电网电压下的鲁棒性如图8所示。即使电网不平衡，A相电流波形仍保持正弦化且电网电流与电压同相，相应的THD值为2.19%，这符合IEEE 519电流谐波极限，如图8（b）和（c）所示。

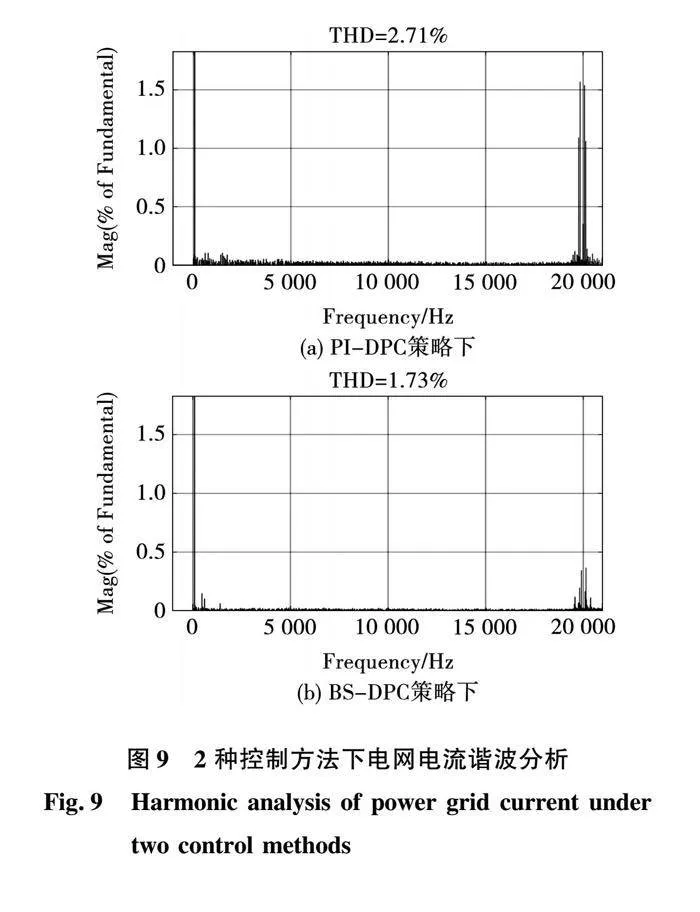
4.3 "THD仿真结果

PI-DPC及BS-DPC两种策略下网侧电流总谐波失真率对比如图9（a）和（b）所示。由图9可看出，由于电网侧使用了电感滤波器，在两种控制方法下，开关频率（20 kHz）附近都存在奇次谐波和高次谐波，所提BS-DPC方案可以将PI控制的THD值（2.71%）提高到1.73%，符合IEEE 519电流失真极限。

传统PI-DPC策略以其结构简单、成本低廉等广泛应用于工程实际中，然而，若受控对象是高度耦合、非线性和系统参数不确定的，采用基于线性化模型的PI-DPC策略瞬态响应速度慢、抗扰性差。而所提BS-DPC方案，其控制器设计基于Lyapunov稳定性理论，设计相应控制律使控制误差随时间增长渐进收敛至零。因此，所提BS-DPC方案对有功和无功功率的控制精度优于传统PI-DPC策略，特别是在系统参数不确定情况下。

3 实验验证

为验证上述分析的正确性，搭建一台2 kW的HFLMC实验平台进行实验验证。开关管采用型号为C3M0065090J的宽禁带SiC MOSFET器件；主控制器采用TMS320F28335PGFA型DSP芯片，其输出信号送入EPM1270T144C5N型CPLD进行逻辑解码，实验平台硬件参数与仿真参数一致，如表2所示。

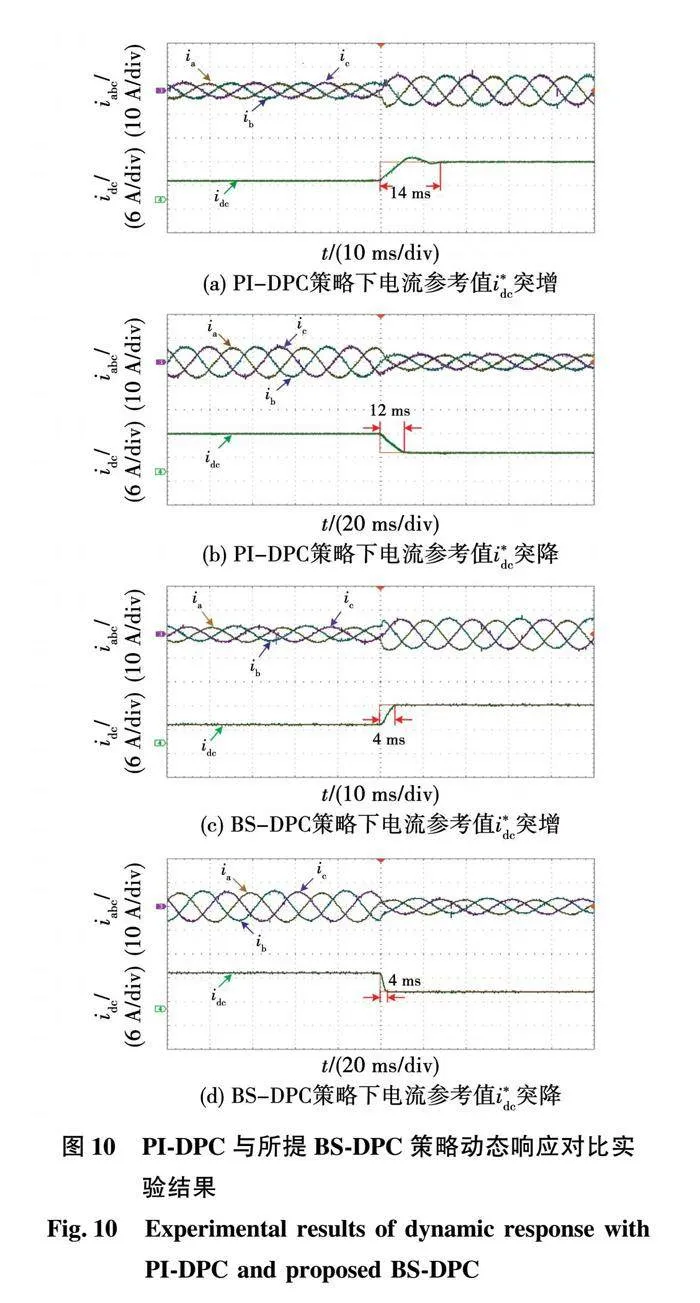
设置2种方案对比传统PI-DPC方法与所提BS-DPC方法的动态跟踪性能。方案一：输出电流参考值i* dc从5 A增加到10 A；方案二：输出电流参考值i* dc从10 A切换到5 A。如图10（a）、（b）所示，在PI-DPC策略下，输出电流idc的瞬态响应上升和下降时间分别为14 ms和12 ms；如图10（c）、（d）所示，在所提BS-DPC策略下，输出电流idc的瞬态响应上升和下降时间均降低至4 ms，输出电流几乎没有过冲；因此，所提BS-DPC策略具有更快的动态响应速度，可快速跟踪输出电流参考值。

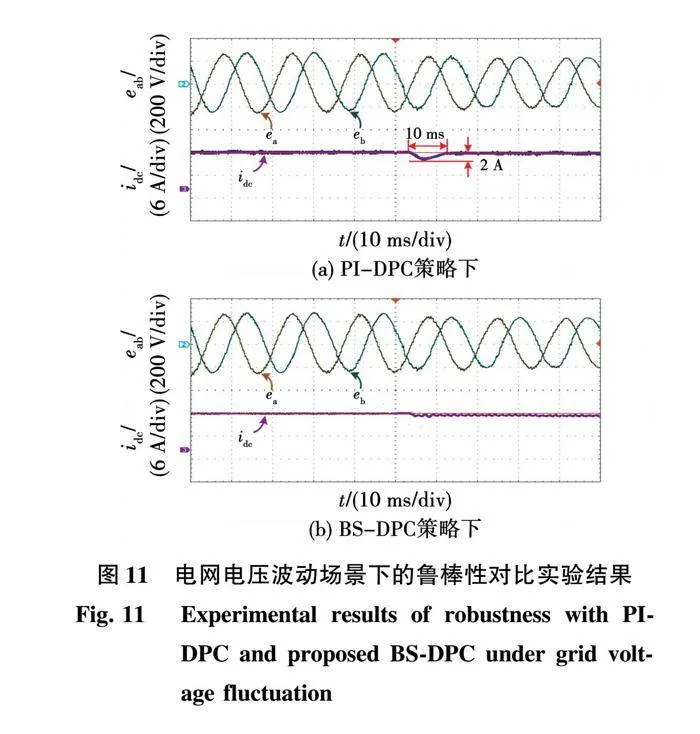
图11对比了电网变化场景下采用PI-DPC与所提BS-DPC方法的实验结果。输出电流参考值i* dc始终设定为10 A，当电网电压减小时，传统PI-DPC策略下输出电流idc波动值为2 A，并在10ms后达到稳态；相反，在所提BS-DPC策略下，idc几乎没有过冲并在1 ms内达到稳态，对比结果表明，所提BS-DPC方法比PI-DPC方法对电网变化具有更强的鲁棒性。

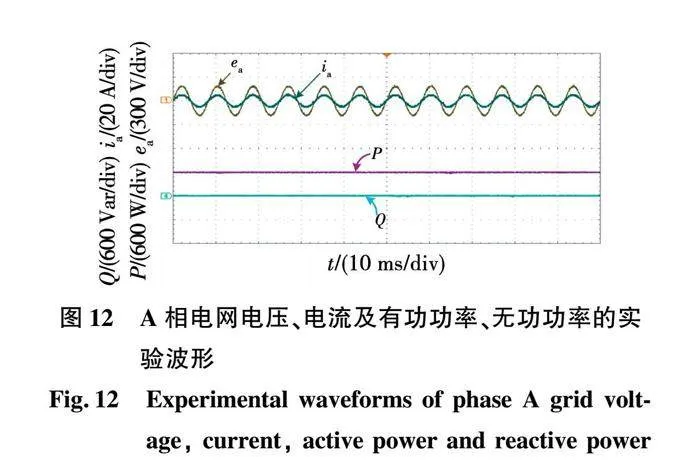
图12为A相电网电压、电流及有功功率、无功功率的实验波形。所设计的反步控制器能对无功功率进行独立控制，有功功率准确跟踪参考值，无功功率保持为0。实验结果可知，电网侧电压电流同相位，实现了单位功率因数。

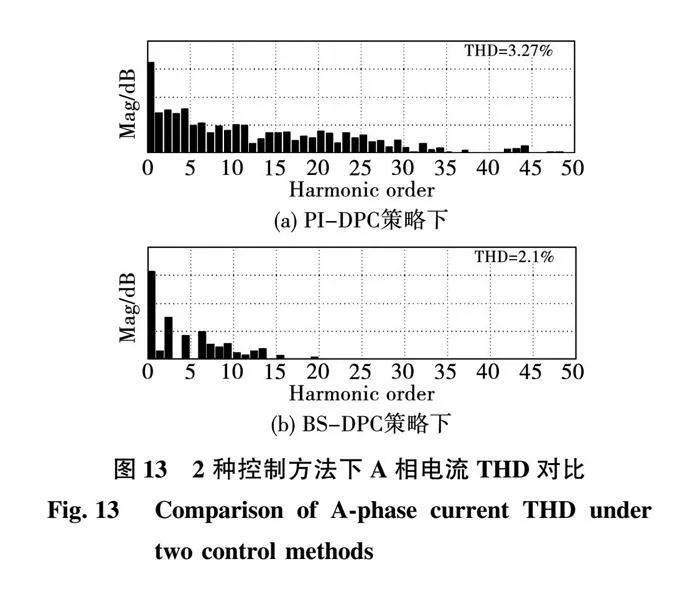
图13对比了PI-DPC及BS-DPC两种控制策略下的网侧电流THD。在传统PI-DPC方法控制下，THD为3.27%；在BS-DPC方法控制下，THD降低至2.1%。与PI-DPC方法产生的谐波阶次相比，所提BS-DPC的A相电流中的谐波阶数要少得多，因此谐波含量较传统PI-DPC策略有所减少。

4 结 "论

本研究提出一种基于非线性反步法的直接功率控制策略（BS-DPC），并验证了其正确性和有效性。仿真和实验结果表明：

1）考虑系统参数不确定性，BS-DPC策略实现了有功功率和无功功率的解耦控制，简化了控制器的参数整定。

2）与传统PI-DPC策略相比，BS-DPC策略控制的有功和无功功率跟踪动态响应速度更快以及对电网波动、直流滤波电感变化的鲁棒性更强，有效降低了网侧电流总谐波失真率，通过调节瞬时无功功率可实现单位功率因数和任意相位差控制。

3）直接功率非线性反步控制策略在电动汽车充电器、电池储能和光伏微电网等领域的电力电子变换器控制中具有很大潜力。

参 考 文 献：

[1] International Energy Agency. Global EV outlook 2022[R]. Paris： IEA， 2022.

[2] KUMAR R， SINGH B. Matrix converter based three phase isolated EV charger with direct power control[C]//2020 IEEE International Conference on Power Electronics， Drives and Energy Systems （PEDES）， December 16-19， 2020， Jaipur， India. 2020： 1.

[3] VARAJAO D， ARAUJO R E， MIRANDA L M， et al. Modulation strategy for a single-stage bidirectional and isolated AC–DC matrix converter for energy storage systems[J]. IEEE Transactions on Industrial Electronics， 2018， 65（4）： 3458.

[4] 王辉， 孙梅迪， 黄守道， 等. 高频链矩阵整流器的研究综述[J]. 电网技术， 2017， 41（3）： 969.

WANG Hui， SUN Meidi， HUANG Shoudao， et al. A review of high-frequency link matrix rectifier[J]. Power System Technology， 2017， 41（3）： 969.

[5] 梅杨， 鲁乔初， 黄伟超. 双向隔离型AC-DC矩阵变换器的软开关复合调制策略[J]. 中国电机工程学报， 2021， 41（7）： 2474.

MEI Yang， LU Qiaochu， HUANG Weichao. Soft-switching composite modulation strategy for bidirectional isolated AC-DC matrix converters[J]. Proceedings of the CSEE， 2021， 41（7）： 2474.

[6] LI X， WU F， YANG G， et al. Dual-period-decoupled space vector phase-shifted modulation for DAB-based three-phase single-stage AC-DC converter[J]. IEEE Transactions on Power Electronics， 2020， 35（6）： 6447.

[7] AFSHARIAN J， XU D D， WU B， et al. The optimal PWM modulation and commutation scheme for a three-phase isolated buck matrix-type rectifier[J]. IEEE Transactions on Power Electronics， 2018， 33（1）： 110.

[8] 刘洪华.双向隔离型AC-DC矩阵变换器控制策略研究[D].湖南：湘潭大学，2021.

[9] 李祥杰.高频链矩阵变换器高性能控制策略研究[D].济南：山东大学，2022.

[10] XIAO X， ZHANG Y， SONG X， et al. Virtual flux direct power control for PWM rectifiers based on an adaptive sliding mode observer[J]. IEEE Transactions on Industry Applications， 2018， 54（5）： 5196.

[11] SONG J， FU C， ZHANG G， et al. Backstepping control of high-frequency link matrix rectifier for battery chargers[J]. IEEE Transactions on Power Electronics， 2021， 36（9）： 10801.

[12] 宋金秋， 段彬， 付程， 等. 电网不平衡工况下高频链矩阵变换器非线性反步控制策略[J]. 中国电机工程学报， 2022， 42（2）： 761.

SONG Jinqiu， DUAN Bin， FU Cheng， et al. Nonlinear backstepping control strategy for high-frequency link matrix converter under unbalanced grid conditions[J]. Proceedings of the CSEE， 2022， 42（2）： 761.

[13] XIAN B， GUO J， ZHANG Y. Adaptive backstepping tracking control of a 6-DOF unmanned helicopter[J]. IEEE/CAA Journal of Automatica Sinica， 2015， 2（1）： 19.

[14] CHENG Peng， YUE Bai， XUN Gong， et al. Modeling and robust backstepping sliding mode control with Adaptive RBFNN for a novel coaxial eight-rotor UAV[J]. IEEE/CAA Journal of Automatica Sinica， 2015， 2（1）： 56.

[15] 杨立本， 章卫国， 黄得刚， 等. 欠驱动四旋翼飞行器反演模糊自适应控制[J]. 西北工业大学学报， 2015， 33（3）： 495.

YANG Liben， ZHANG Weiguo， HUANG Degang， et al. Adaptive fuzzy backstepping control for underactuated quadrotor UAV[J]. Journal of Northwestern Polytechnical University， 2015， 33（3）： 495.

[16] RASTEGAR Fatemi S M J， ABJADI N R， SOLTANI J， et al. Speed sensorless control of a six-phase induction motor drive using backstepping control[J]. Iet Power Electronics， 2014， 7（1）： 114.

[17] YU J， SHI P， DONG W， et al. Neural network-based adaptive dynamic surface control for permanent magnet synchronous motors[J]. IEEE Transactions on Neural Networks and Learning Systems， 2015， 26（3）： 640.

[18] ROY T K， MAHMUD M A， OO A M T， et al. Nonlinear adaptive backstepping controller design for islanded DC microgrids[J]. IEEE Transactions on Industry Applications， 2018， 54（3）： 2857.

[19] ZUNIGA Ventura Y A， LANGARICA Cordoba D， LEYVA-RAMOS J， et al. Adaptive backstepping control for a fuel cell/boost converter system[J]. IEEE Journal of Emerging amp; Selected Topics in Power Electronics， 2018， 6（2）： 686.

[20] JONG R W， YAN Y. Design of backstepping direct power control for three-phase PWM rectifier[J]. IEEE Transactions on Industry Applications， 2019， 55（3）： 3160.

[21] 夏志鹏， 金平， 常岭. 高频链式矩阵变换器的最小功率回流控制[J]. 电机与控制学报， 2022， 26（4）： 89.

XIA Zhipeng， JIN Ping， CHANG Ling. Minimum power reflux control for high frequency link matrix converter[J]. Electric Machines and Control， 2022， 26（4）： 89.