基于转矩跟踪电流误差校正的压缩机转速脉动抑制算法研究

摘 "要：针对空调用永磁压缩机在低频运行中存在转速脉动大、振动噪声高等问题，提出一种基于转矩跟踪电流误差校正的压缩机转速脉动抑制算法。首先，对压缩机的周期性转速脉动进行分析，并根据转速脉动特性建立转速环控制系统模型。然后，引入迭代学习算法，获得转矩跟踪电流，在此基础上，提出特征滤波函数，用来提取转矩跟踪电流基波分量，有效抑制特定次频率的转速脉动，同时引入转矩跟踪电流误差校正律，对转矩跟踪电流与参考交轴电流的误差进行校正，进一步获得前馈补偿电流，并施加到参考交轴电流中，该算法可以消除传统迭代学习转矩跟踪电流存在的误差累积，跟踪性能好。最后，在空调压缩机实验平台上对算法进行验证，实验结果表明，采用该算法可以显著抑制压缩机的转速脉动。

关键词：压缩机系统；低频转速脉动；特征滤波函数；转矩跟踪电流误差校正律；迭代学习

DOI：

中图分类号：TM351 " " " " " 文献标志码：A " " " " "文章编号：

Research on speed ripple suppression algorithm of compressor motor based on torque tracking current error correction

YANG Zhebin1， DENG Rongfeng1， ZHANG Xiaojun1， YANG Jiaqiang1， GU Tangtang2，

ZHUO Senqing2

（1. College of Electrical Engineering， Zhejiang University， Hangzhou 310027， China;

2. Ningbo AUX Electrical Limited Company， Ningbo 315191， China）

Abstract： The speed ripple suppression algorithm of compressor motor based on torque tracking current error correction is proposed to address the issues of large torque ripple and high vibration noise in the operation of a permanent magnet compressor for air conditioning. Initially， based on the characteristics of the torque ripple， an analysis of the compressor's periodic speed ripple is conducted. The iterative learning control approach is employed to obtain torque tracking current. On this basis， the optimized filtering function is introduced to extract the fundamental component of the torque tracking current. At the same time， the torque tracking current error correction law is introduced to correct the error between the torque tracking current and the reference torque current， and the feedforward compensation current is obtained and fed forward to the control system. The error accumulation of traditional iterative learning torque tracking current is eliminated， and the compressor speed ripple is effectively suppressed. Finally， The algorithm is validated on an experimental platform for air conditioning compressors， and the experimental results demonstrate effectively mitigating compressor torque ripple.

Keywords： compressor system; low frequency speed ripple; characteristic filter function; torque tracking current error correction law; iterative learning

0 引 "言

目前，压缩机作为空调系统的主要核心部件，其内部电机采用永磁同步电机（permanent magnet synchronous motor， PMSM），与其他电机相比，具有功率因数高、运行性能好等优点[1-4]。然而空调行业为了降低成本通常采用单转子压缩机，由于不对称曲轴设计，在一个周期内受到吸气压缩、吸气排气的影响，导致负载产生周期性转矩脉动，从而引起压缩机的周期性转速脉动。

压缩机转速脉动一直是空调行业的关键技术难题，容易造成系统振动与噪声，所以必须采取有效措施对转速脉动进行抑制，目前常见方法有电机优化设计[5]，对电机本体进行斜槽、斜极设计，但是针对单转子压缩机的负载特性，这种转速脉动抑制效果较差；另一种是电机优化控制[6-7]，通过控制电机参考交轴电流，实现电磁转矩的补偿，最终达到转速脉动抑制效果。

为了抑制空调压缩机转速脉动，国内外学者针对压缩机优化控制方法进行了大量的研究。文献[8-9]提出傅里叶变换补偿法，对转速进行傅里叶分解，提取转速基波量进行补偿。该方法需要进行查表离线补偿，不同类型的压缩机初始相位不一致，需要对初始相位进行调节，算法通用性差。文献[10-12]提出重复控制补偿算法，可用于跟踪或消除周期信号的误差，通过补偿控制延迟来实现周期性扰动抑制，但是该方法只能针对固定运行频率进行扰动抑制，当运行频率改变时，需要重新调整参数。文献[13-15]提出负载转矩观测算法，观测器可以对扰动转矩进行前馈补偿，够实时观测电机受到的时变且难以预测的扰动。但是观测出的负载转矩存在一定的相位延迟，且对于电机模型参数的依赖性较高。文献[16-17]提出迭代学习控制算法，获得转矩跟踪电流，并前馈到控制系统。这种方法对于周期性转速脉动抑制效果好，但获得的转矩跟踪电流存在误差累积。文献[18]提出基于分数阶比例微分迭代学习控制算法（proportional differential iterative learning control， PDILC），系统的高频谐波分量得到补偿，有效抑制周期性转速脉动，但是分数阶的参数配置复杂且容易造成参数摄动。文献[19]引入无模型自适应迭代学习算法，摆脱对于精确模型的依赖，但是算法复杂，程序执行时间长。在实际工况中，受到温度、环境等因素的影响，导致上述文献[16-19]的迭代学习控制算法获得的转矩跟踪电流补偿量均存在误差累积，压缩机转速脉动抑制效果受限。

在上述文献研究的基础上，本文提出一种基于转矩跟踪电流误差校正的压缩机转速脉动抑制算法（error correction iterative learning control， ECILC），首先对压缩机转速脉动的各次脉动分量进行分析，建立转速环控制系统模型。在迭代学习基础上，提出特征滤波函数，分析扰动项的零极点分布，提取转矩跟踪电流基波分量，参数配置遵循零极点对消原则，该方法与传统迭代学习算法相比，对于特定次频率的转速脉动抑制效果显著，算法跟踪性能好。同时引入转矩跟踪电流误差校正律，对转矩跟踪电流进行校正，获得前馈补偿电流，并施加到参考交轴电流中，消除了传统迭代学习转矩跟踪电流存在的误差累积，无需查表离线补偿，参数适应性强，算法稳定性能好。最后在压缩机实验平台上验证了算法控制策略的有效性，实验结果表明，采用该算法能有效抑制压缩机低频转速脉动。

1.1 压缩机转速脉动分析

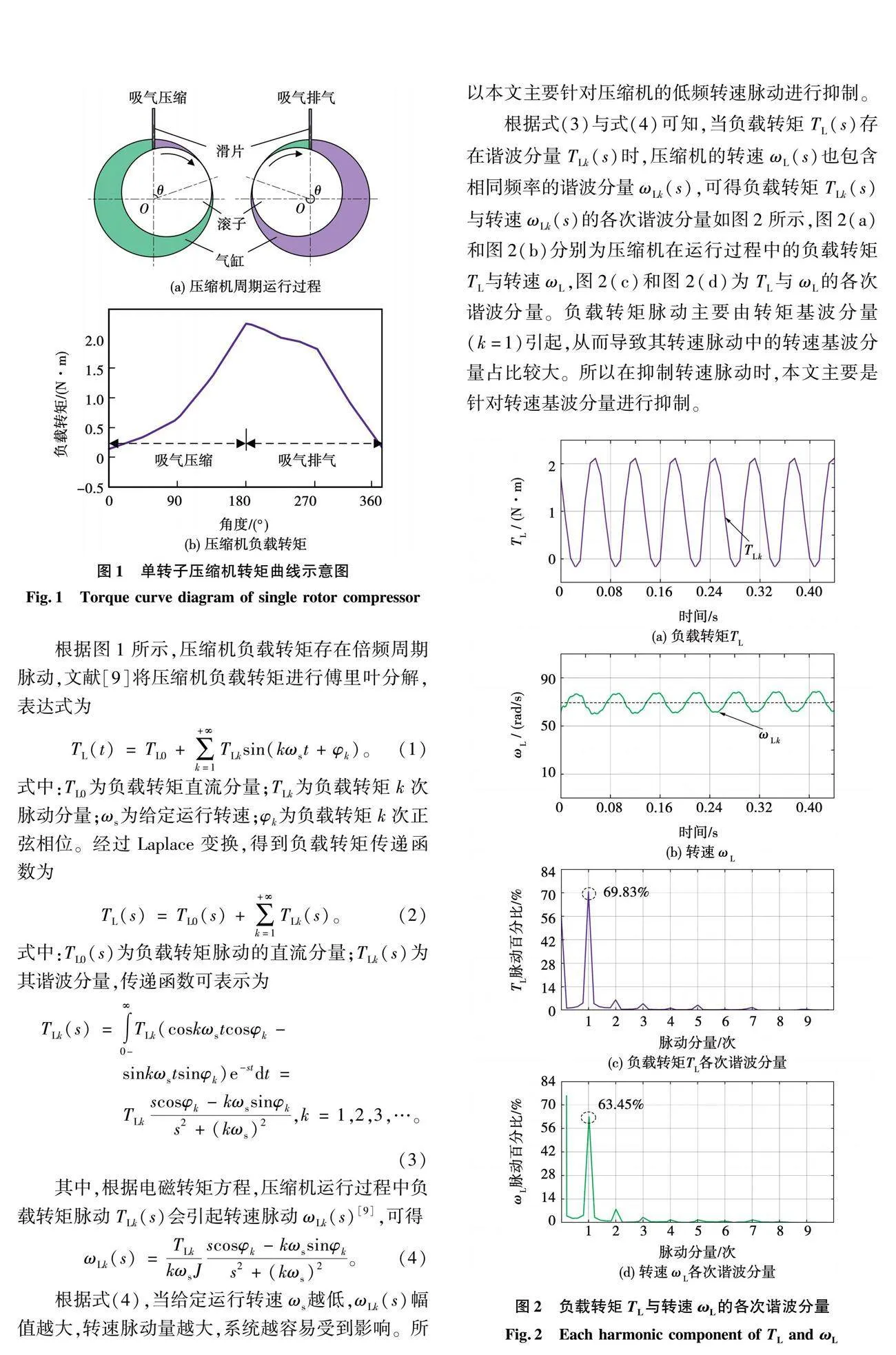
单转子压缩机采用不对称曲轴设计，在一个周期内受到吸气压缩、吸气排气的影响，产生不同的气体阻力，导致压缩机负载产生周期性的转矩脉动。单转子压缩机转矩曲线如图1所示，图1（a）和图1（b）分别为压缩机周期运行过程（吸气压缩、吸气排气）与压缩机负载转矩。

根据图1所示，压缩机负载转矩存在倍频周期脉动，文献[9]将压缩机负载转矩进行傅里叶分解，表达式为

。 （1）

式中：TL0为负载转矩直流分量；TLk为负载转矩k次脉动分量；ωs为给定运行转速；φk为负载转矩k次正弦相位。经过Laplace变换，得到负载转矩传递函数为

。 （2）

式中：TL0（s）为负载转矩脉动的直流分量；TLk（s）为其谐波分量，TLk（s）的传递函数可表示为

。 （3）

其中，根据电磁转矩方程，压缩机运行过程中负载转矩脉动TLk（s）会引起转速脉动ωLk（s）[9]，可得

。 （4）

根据式（4），当给定运行转速ωs越低，ωLk（s）幅值越大，转速脉动量越大，系统越容易受到影响。所以本文主要针对压缩机的低频转速脉动进行抑制。

根据式（3）与式（4）可知，当负载转矩TL（s）存在谐波分量TLk（s）时，压缩机的转速ωL（s）也包含相同频率的谐波分量ωLk（s），可得负载转矩TLk（s）与转速ωLk（s）的各次谐波分量如图2所示，图2（a）和图2（b）分别为压缩机在运行过程中的负载转矩TL与转速ωL，图2（c）和图2（d）为TL与ωL的各次谐波分量。负载转矩脉动主要由转矩基波分量（k=1）引起，从而导致其转速脉动中的转速基波分量占比较大。所以在抑制转速脉动时，本文主要是针对转速基波分量进行抑制。

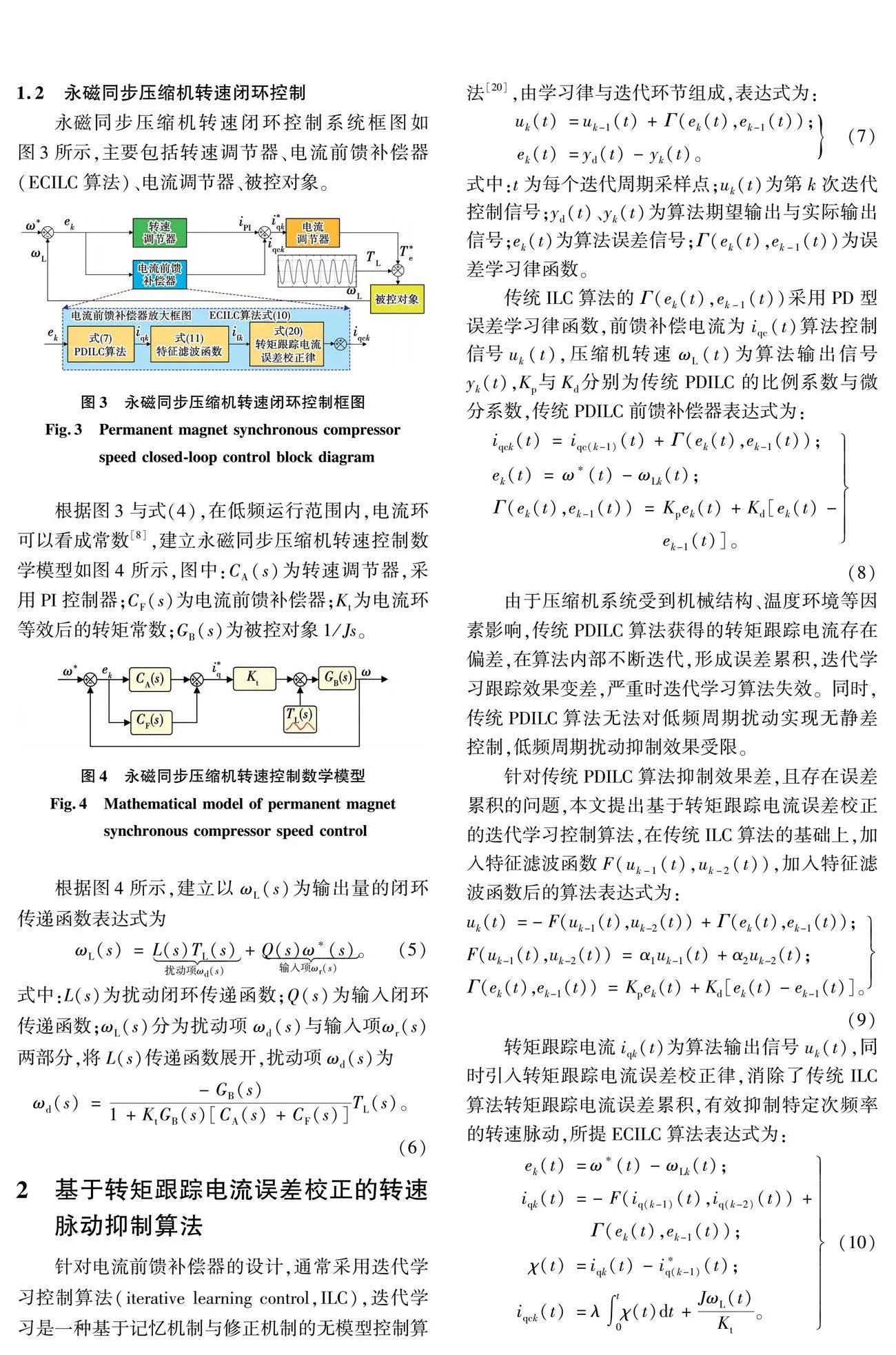
1.2 永磁同步压缩机转速闭环控制

永磁同步压缩机转速闭环控制系统框图如图3所示，主要包括转速调节器、电流前馈补偿器（ECILC算法）、电流调节器、被控对象构成。

根据图3与式（4），在低频运行范围内，电流环可以看成常数[8]，建立永磁同步压缩机转速控制数学模型如图4所示，图中：CA（s）为转速调节器，采用PI控制器；CF（s）为电流前馈补偿器；Kt为电流环等效后的转矩常数；GB（s）为被控对象1 / Js。

根据图4所示，建立以ωL（s）为输出量的闭环传递函数表达式为

。 （5）

式中：L（s）为扰动闭环传递函数；Q（s）为输入闭环传递函数。ωL（s）分为扰动项ωd（s）与输入项ωr（s）两部分，将L（s）传递函数展开，扰动项ωd（s）为

。 （6）

2 基于转矩跟踪电流误差校正的转速脉动抑制算法

针对电流前馈补偿器的设计，通常采用迭代学习控制算法（iterative learning control， ILC），迭代学习是一种基于记忆机制与修正机制的无模型控制算法[20]，由学习律与迭代环节组成，表达式为：

（7）

式中：t为每个迭代周期采样点；uk（t）为第k次迭代控制信号；yd（t）、yk（t）为算法期望输出与实际输出信号；ek（t）为算法误差信号；Γ（ek（t）， ek-1（t））为误差学习律函数。

传统ILC算法的Γ（ek（t）， ek-1（t））采用PD型误差学习律函数，前馈补偿电流为iqc（t）算法控制信号uk（t），压缩机转速ωL（t）为算法输出信号yk（t），Kp与Kd分别为传统PDILC的比例系数与微分系数，传统PDILC前馈补偿器表达式为：

（8）

由于压缩机系统受到机械结构、温度环境等因素影响，传统PDILC算法获得的转矩跟踪电流存在偏差，在算法内部不断迭代，形成误差累积，迭代学习跟踪效果变差，严重时迭代学习算法失效。同时，传统PDILC算法无法对低频周期扰动实现无静差控制，低频周期扰动抑制效果受限。

针对传统PDILC算法抑制效果差，且存在误差累积的问题，本文提出基于转矩跟踪电流误差校正的迭代学习控制算法，在传统ILC算法的基础上，加入特征滤波函数F（uk-1（t）， uk-2（t）），加入特征滤波函数后的算法表达式为：

（9）

转矩跟踪电流iqk（t）为算法输出信号uk（t），同时引入转矩跟踪电流误差校正律，消除了传统ILC算法转矩跟踪电流误差累积，有效抑制特定次频率的转速脉动，所提ECILC算法表达式为：

（10）

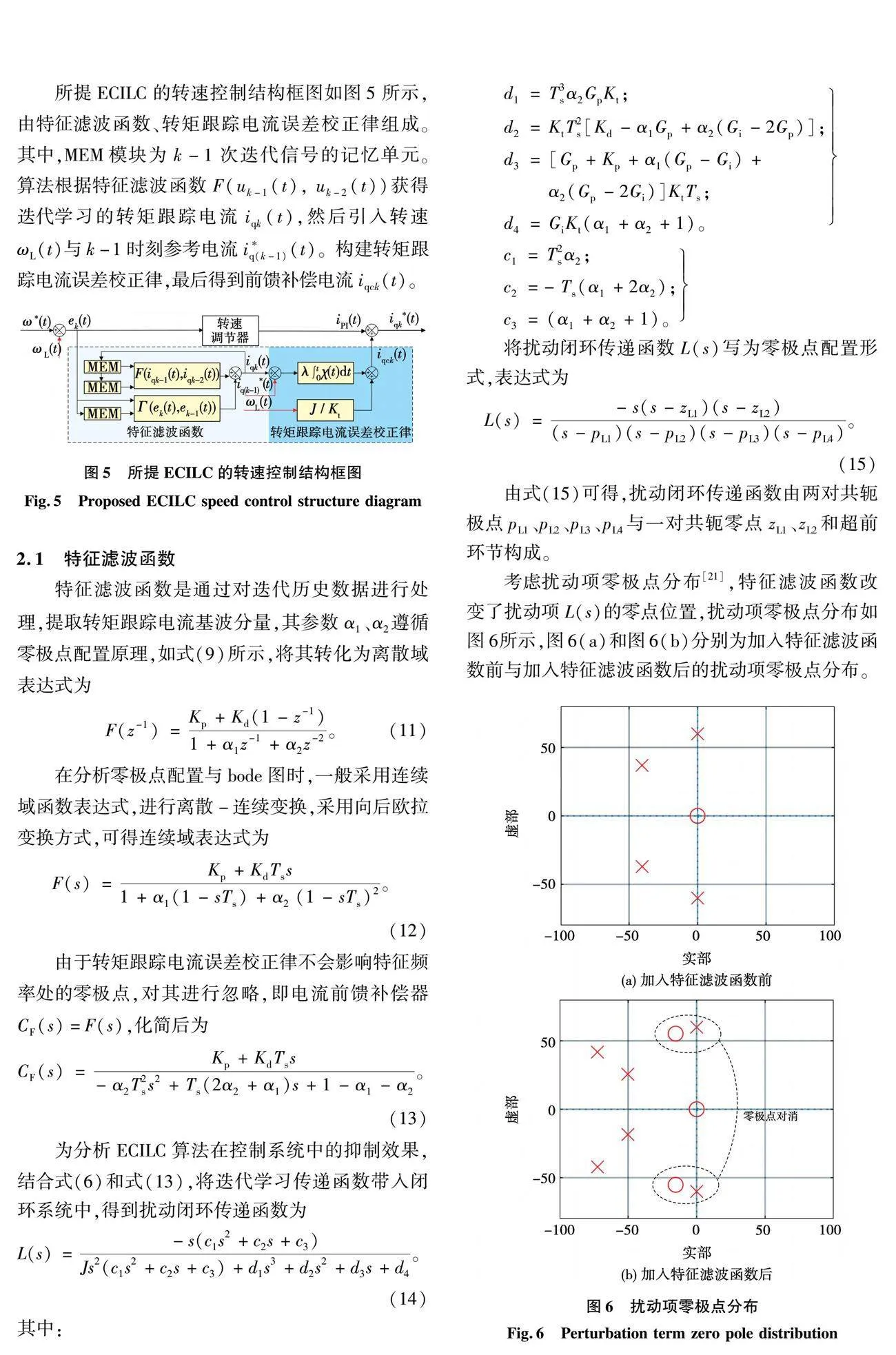
所提ECILC的转速控制结构框图如图5所示，由特征滤波函数、转矩跟踪电流误差校正律组成。其中，MEM模块为k-1次迭代信号的记忆单元。算法根据特征滤波函数F（uk-1（t）， uk-2（t））获得迭代学习的转矩跟踪电流iqk（t），然后引入转速ωL（t）与k-1时刻参考电流iq（k-1）*（t）。构建转矩跟踪电流误差校正律，最后得到前馈补偿电流iqck（t）。

2.1 特征滤波函数

特征滤波函数是通过对迭代历史数据进行处理，提取转矩跟踪电流基波分量，其参数α1、α2遵循零极点配置原理，如式（9）所示，将其转化为离散域表达式为

。 （11）

在分析零极点配置与bode图时，一般采用连续域函数表达式，进行离散-连续变换，采用向后欧拉变换方式，可得连续域表达式为

。 （12）

由于转矩跟踪电流误差校正律不会影响特征频率处的零极点，对其进行忽略，即电流前馈补偿器CF（s）=F（s），化简后为

。 （13）

为分析ECILC算法在控制系统中的抑制效果，结合式（6）和式（13），将迭代学习传递函数带入闭环系统中，得到扰动闭环传递函数为

。 （14）

其中：

将扰动闭环传递函数L（s）写为零极点配置形式，表达式为

。 （15）

由式（15）可得，扰动闭环传递函数由两对共轭极点pL1、pL2、pL3、pL4与一对共轭零点zL1、zL2和超前环节构成。

考虑扰动项零极点分布[21]，特征滤波函数改变了扰动项L（s）的零点位置，扰动项零极点分布如图6所示，图6（a）和图6（b）分别为加入特征滤波函数前与加入特征滤波函数后的扰动项零极点分布。

从图6可以看出，加入特征滤波函数后，扰动项中的L（s）零点位置与扰动项中的TL（s）的极点位置相近，配置特征滤波函数，保证L（s）的共轭零点zL1、zL2接近TL（s）的极点位置，即可有效抑制压缩机的转速脉动。

根据式（14）与图6，将c1s2+c2s+c3设计为s2+2ωcTs2s+ωs2。阻尼频率ωc保证系统有足够带宽，但不能过大，否则会引起零极点位置距离过远，TL（s）的零极点无法对消。参数α1、α2满足：

（16）

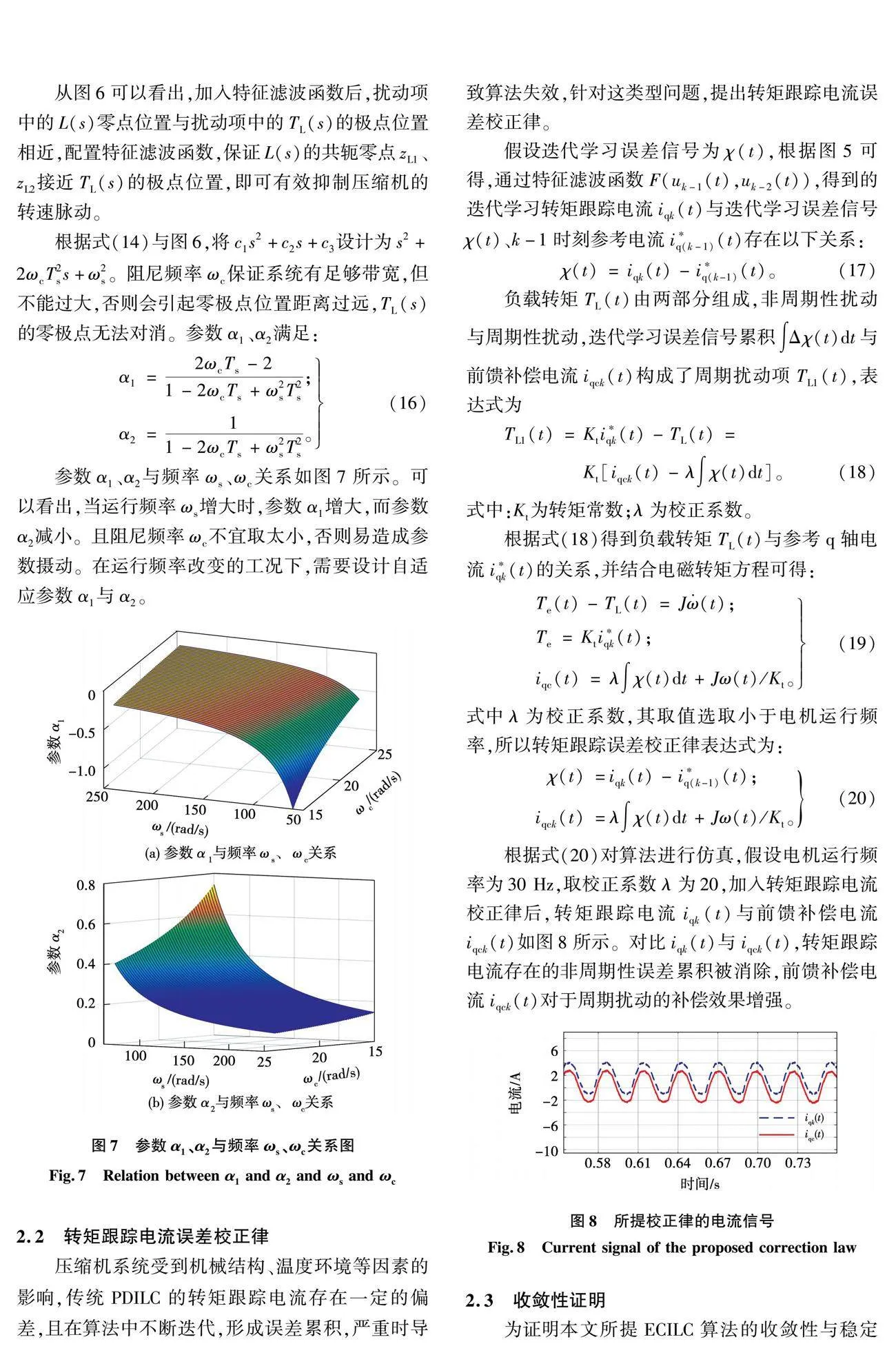
参数α1、α2与频率ωs、ωc关系如图7所示。从图中可以看出，当运行频率ωs增大时，参数α1增大，而参数α2减小。且阻尼频率ωc不宜取太小，否则易造成参数摄动。在运行频率改变的工况下，需要设计自适应参数α1与α2。

（a）参数α1与频率ωs、ωc关系 " "（b）参数α2与频率ωs、ωc关系

图7 "参数α1、α2与频率ωs、ωc关系图

Fig. 7 "Relation between α1 and α2 and ωs and ωc

2.2 转矩跟踪电流误差校正律

压缩机系统受到机械结构、温度环境等因素的影响，传统PDILC的转矩跟踪电流存在一定的偏差，且在算法中不断迭代，形成误差累积，严重时导致算法失效，针对这类型问题，提出转矩跟踪电流误差校正律。

假设迭代学习误差信号为χ（t），根据图5可得，通过特征滤波函数F（uk-1（t）， uk-2（t）），得到的迭代学习的转矩跟踪电流iqk（t）与迭代学习误差信号χ（t）、k-1时刻参考电流iq（k-1）*（t）存在以下关系：

。 （17）

负载转矩TL（t）由两部分组成，非周期性扰动与周期性扰动，迭代学习误差信号累积ʃ χ（t）dt与前馈补偿电流iqck（t）构成了周期扰动项TL1（t），表达式为

（18）

式中：Kt为转矩常数；λ为校正系数。

根据式（18）得到负载转矩TL（t）与参考q轴电流iqk*（t）的关系，并结合电磁转矩方程可得：

（19）

式中λ为校正系数，其取值选取小于电机运行频率，所以转矩跟踪误差校正律表达式为：

（20）

根据式（20）对算法进行仿真，假设电机运行频率为30Hz，取校正系数λ为20，加入转矩跟踪电流校正律后，转矩跟踪电流iqk（t）与前馈补偿电流iqck（t）如图8所示。对比iqk（t）与iqck（t），转矩跟踪电流存在的非周期性误差累积被消除，前馈补偿电流iqck（t）对于周期扰动的补偿效果增强。

2.3 收敛性证明

为证明本文所提ECILC算法的收敛性与稳定性，将式（20）的积分项进行消除，可化简为

。 （21）

设ECILC算法的控制信号uk（t）为前馈补偿电流iqck（t），状态信号xk（t）为转矩跟踪电流iqk（t），转速控制系统的输出信号yk（t）为实际转速信号ωL（t）。且λ取值小于电机运行频率，所以λ˂1/Ts。我们期望参考电流iqk*（t）轨迹按照转矩补偿电流iqck（t）轨迹流动，iqck（t）-iqc（k-1）（t）≈iqk*（t）-iq（k-1）*（t），结合式（10），可得

（22）

其中：

参数α1、α2的值见式（16），Δuk（t）=uk（t）-uk-1（t），由于转矩跟踪电流存在误差，所以Δxk（t）gt; Δuk（t）。两端同时取范数，可得

（23）

根据迭代学习高阶学习律定理[22]，存在ρigt;0（i=0，1，…，N），使得‖αi-1 + βiKt / J‖≤ρi，且多项式z3-ρ1z2-ρ2z-ρ3的所有零点均在单位圆内，则当初态xk（t）=xd（0），则ECILC算法产生的迭代输出一致收敛于期望轨迹。

3 实验结果

为验证本文提出的基于转矩跟踪电流误差校正的压缩机转速脉动抑制算法策略的有效性，搭建压缩机测试平台如图9所示，并进行实验验证。在该平台上对传统PDILC算法与本文提出的ECILC算法进行实验对比，实验压缩机用PMSM控制系统参数如表1所示，采用DSP芯片TMS320F28335作为控制器，其开关频率为10kHz，电流环执行周期为100μs，转速执行周期为1ms。

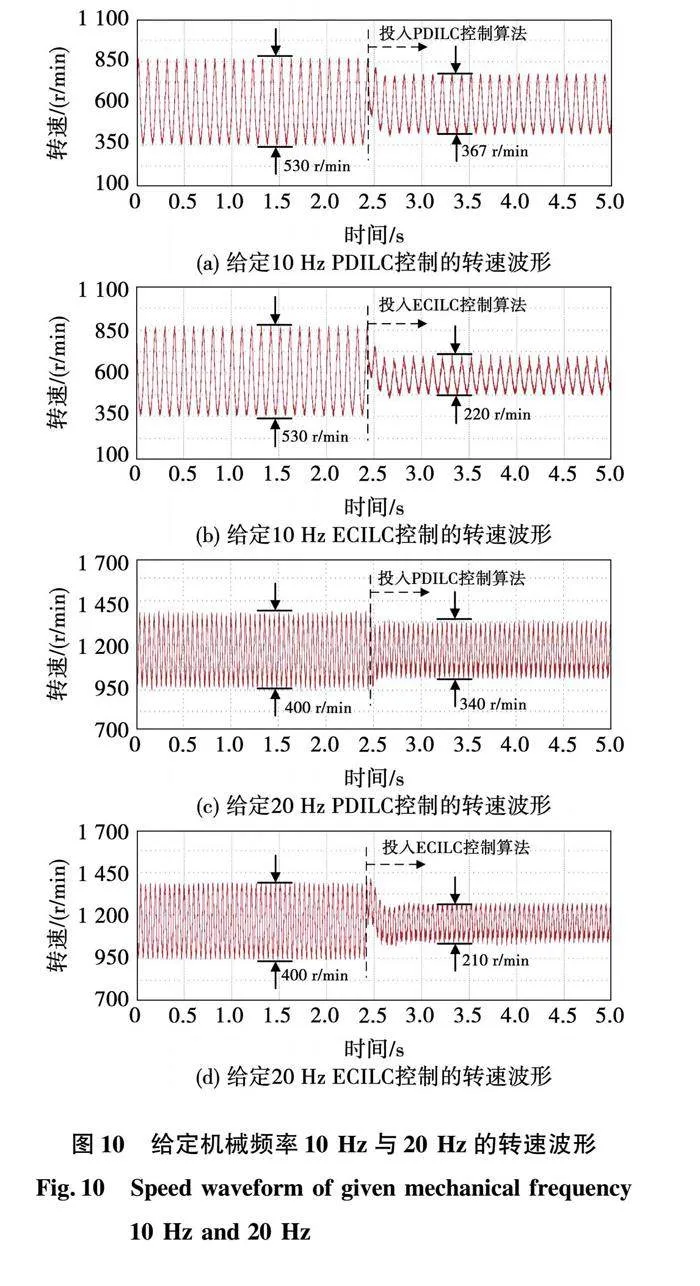
给定机械频率10Hz与20Hz下，传统PDILC控制和所提ECILC控制的转速波形如图10所示。可以看出，在10Hz下，传统PDILC控制算法将转速脉动峰峰值从530r/min抑制到367r/min，而所提ECILC控制算法可以抑制到220r/min。在20Hz下，传统PDILC将转速脉动峰峰值从400r/min抑制到340r/min，而所提ECILC控制算法可以抑制到210r/min。与传统PDILC控制算法相比，所提ECILC控制算法的转速脉动抑制效果更显著。

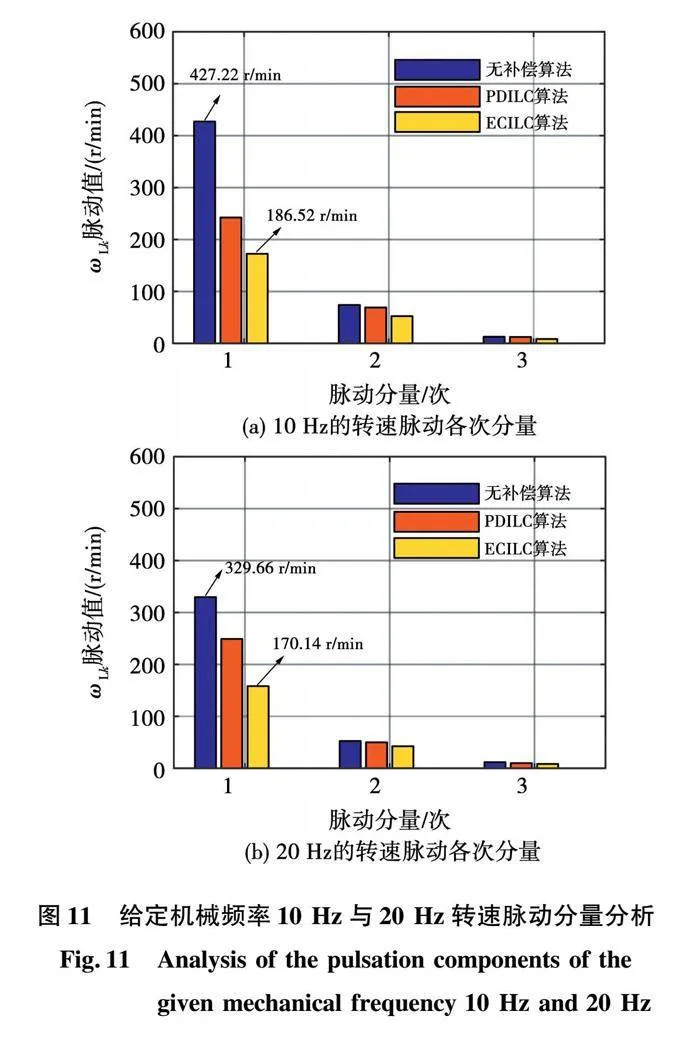
给定机械频率10Hz与20Hz转速脉动分量分析如图11所示。图11（a）和图11（b）分别为给定机械频率10Hz和20Hz的转速脉动各次分量。从图11可以看出，所提ECILC控制算法的转速脉动基波分量分别为186.52r/min（给定10Hz）和170.14r/min（给定20Hz），比传统PDILC控制算法的转速基波分量少，且相较于无补偿算法可以抑制1/3左右，而对于其他次脉动分量，所提ECILC算法抑制效果一般，说明所提ECILC控制算法主要是通过抑制转速基波分量，来抑制压缩机转速脉动。

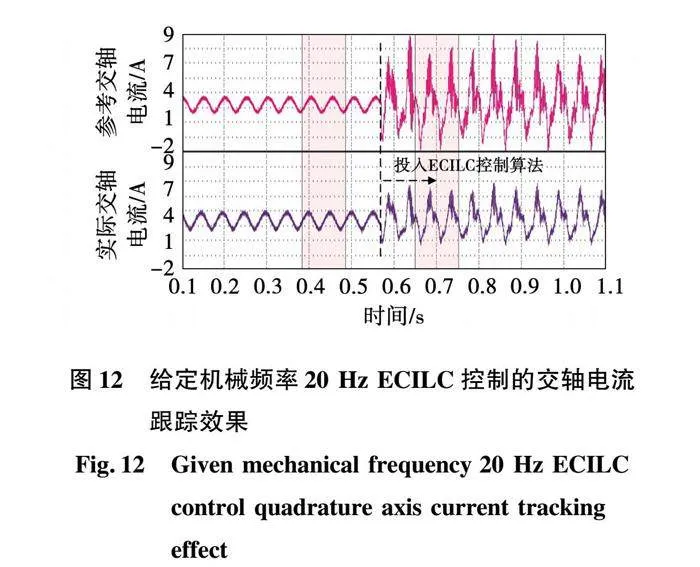
给定机械频率20Hz ECILC控制的交轴电流跟踪效果如图12所示。从图中可以看出，实际交轴电流iq按照参考交轴电流iq*轨迹进行实时跟踪，且在加入ECILC控制算法后，相当于注入电流谐波，实际交轴电流的iq谐波含量增加，所以本文所提的ECILC控制算法会导致电机部分铜耗增加。

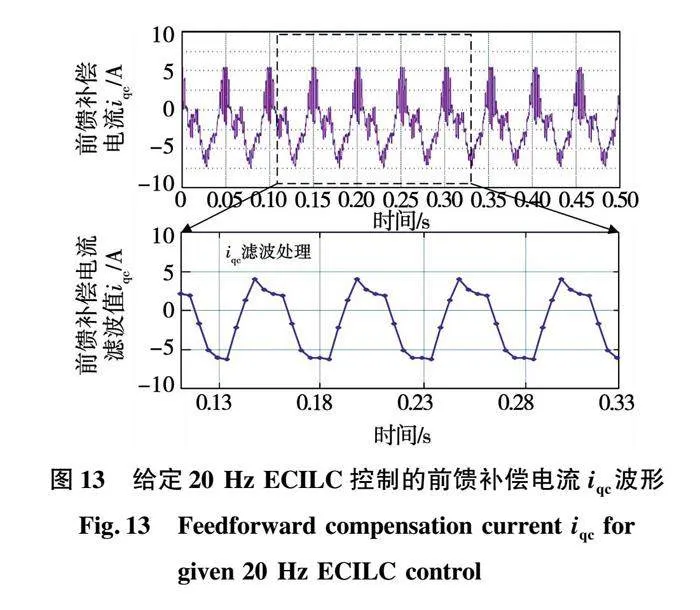
给定机械频率20Hz ECILC控制的前馈补偿电流iqc波形如图13所示。从图中可以看出，在加入所提的ECILC算法后，前馈补偿电流中存在高频次谐波分量。将前馈补偿电流iqc进行采样滤波处理，其波形与图1（b）所示的压缩机负载转矩曲线类似，证明前馈补偿电流可以跟踪压缩机负载转矩，从而抑制压缩机的转速脉动。

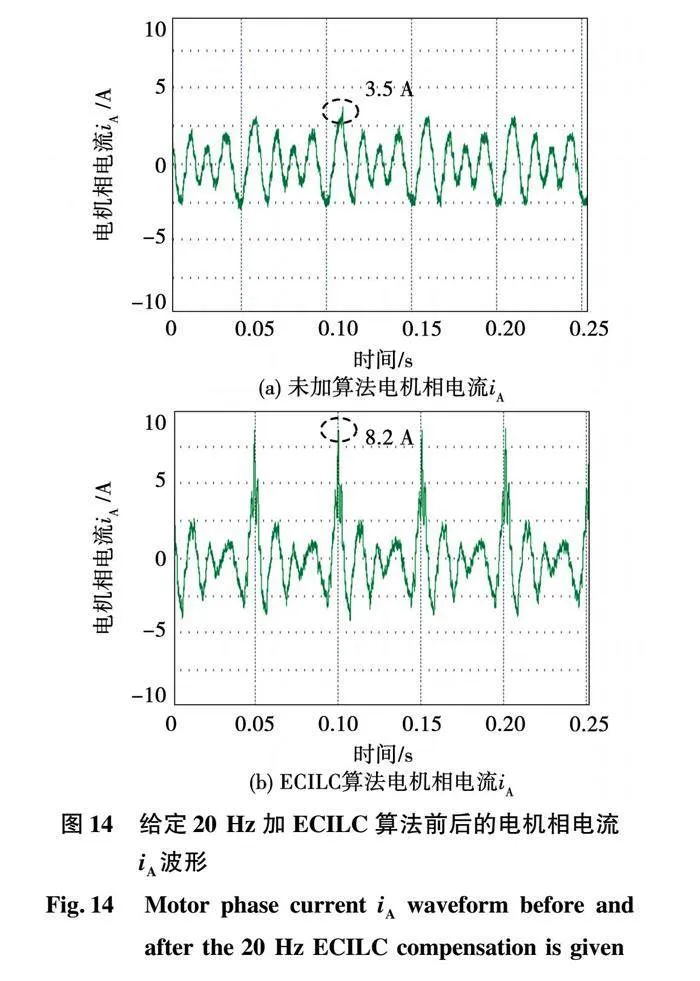
给定20Hz加ECILC算法前后的电机相电流iA波形如图14所示，从图中可以看出，加ECILC算法后，电机相电流中存在高频次谐波分量。未加转速脉动抑制算法与加ECILC算法相比，其相电流iA最大振幅值增大4.7A，主要原因是由单转子压缩机负载转矩峰值引起的，说明ECILC控制算法可以有效抑制压缩机负载转矩峰值，从而抑制压缩机的转速脉动。

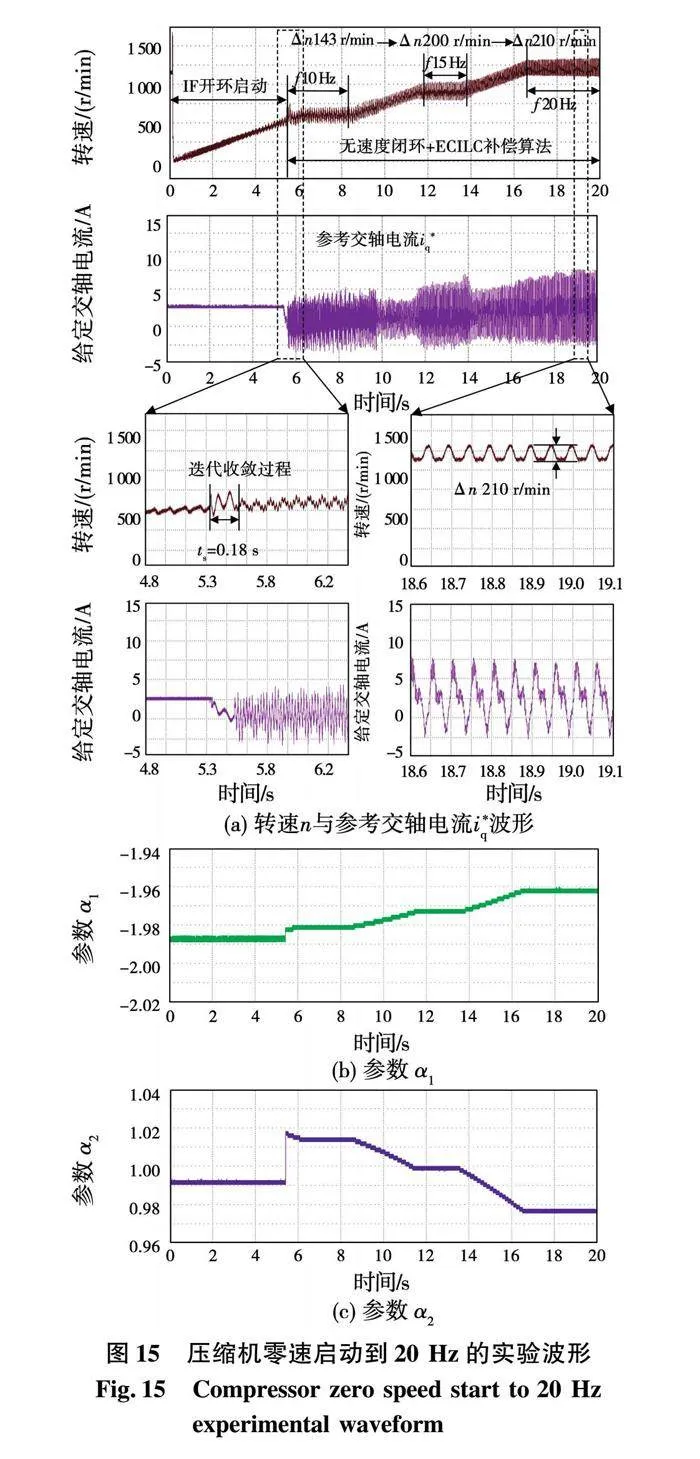
压缩机零速启动到20Hz的实验波形如图15所示，其中，图15（a）～图15（c）分别为转速n与参考电流iq*波形、参数α1、参数α2。运行频率按照0到10Hz到15Hz再到20Hz变化。从0到10Hz采用电流频比控制，即IF开环启动，在10Hz后投入无速度闭环算法与ECILC补偿算法。从图15可以看出，所提ECILC算法的转速脉动峰峰值在250r/min以下（10～20Hz），与图10未加转速脉动抑制算法时转速脉动峰峰值在530r/min（10Hz）、400r/min（20Hz）相比，转速脉动抑制效果显著；且算法在0.18s后可以快速收敛；同时，参数α1与α2适应运行频率fs变化，证明所提ECILC控制算法动态过程中具有良好的转速脉动抑制效果。

为进一步评估算法在低频运行频率范围内的转速脉动抑制效果，定义转速脉动抑制率，表达式为

。 （24）

式中 、 为无抑制算法、有抑制算法的转速纹波极差。转速脉动抑制率越低，转速脉动抑制效果越好。

给定10～30Hz两种算法转速脉动抑制率对比如图16所示。从图中不难看出，在整个低频运行频率范围内，所提的ECILC控制算法的转速脉动抑制率始终低于传统PDILC控制算法，ECILC抑制效果显著，但是随着压缩机运行频率的升高，两种控制方法的转速脉动抑制率也升高，这主要原因是由于高频运行受到转动惯量的影响较小，导致转速脉动较小，抑制效果变差。

4 结 "论

本文以抑制压缩机低频转速脉动为目标，研究了一种基于转矩跟踪电流误差校正的压缩机转速脉动抑制算法。通过与传统迭代学习转速脉动抑制算法进行理论分析、实验对比，得出如下结论：

1）本文所提的转速脉动抑制算法引入特征滤波函数，用来提取转矩电流基波分量，与传统迭代学习转速脉动抑制算法相比，压缩机在特定次频率处的转速脉动抑制效果更显著。

2）在引入特征滤波函数的基础上，提出转矩跟踪电流误差校正律，对转矩跟踪电流与参考交轴电流的误差进行校正，消除了传统迭代学习转矩跟踪电流存在的误差累积，算法跟踪性能好。

3）实验结果证明采用本文所提的转速脉动抑制算法在低频运行过程中参数可以实现自适应变化，无需查表离线补偿，且转速脉动抑制效果显著，算法稳定性好。

参 考 文 献：

[1] 张晓军，杨家强，杨昊林. 一种基于永磁同步电机绕组铜耗功率最大的电动汽车母线电容放电方法[J]. 中国电机工程学报，2022，42（17）： 6460.

ZHANG Xiaojun，YANG Jiaqiang，YANG Haolin，et al．A DC-bus capacitor discharge method based on maximum copper consumption power of permanent magnet synchronous motor windings in electric vehicles [J]．Proceedings of the CSEE，2022，42（17）： 6460.

[2] 兰志勇，李延昊，罗杰，等.一种自适应扩展卡尔曼滤波的永磁同步电机无位置传感器矢量控制[J].电机与控制报，2024，28（3）： 141.

LAN Zhiyong，LI Yanhao，LUO Jie，et al．Sensorless vector control of permanent magnet synchronous motor based on adaptive extended Kalman filter [J]．Electric Machines and Control，2024，28（3）： 141．

[3] 黄万奔，杨家强，邓鎔峰，等．高功率因数无电解电容永磁电机变频系统逆变器电流控制策略[J]．电机与控制学报，2022，26（8）： 1．

HUANG Wanben，YANG Jiaqiang，DENG Rongfeng，et al．Inverter current control strategy for high power factor electrolytic capacitor-less permanent magnet motor drive system[J]．Electric Machines and Control，2022，26（8）： 1．

[4] ZHAO N，WANG G，LI B，et al．Beat phenomenon suppression for reduced DC-link capacitance IPMSM drives with fluctuated load torque[J]．IEEE Transactions on Industrial Electronics，2018，66（11）： 8334．

[5] 宋守许，李诺楠，杜毅等．抑制永磁同步电机转速脉动的转子再设计方法[J]．中国机械工程，2019，30（17）： 2084．

SONG Shouxu，LI Nuonan，DU Yi，et al．Rotor redesign method for suppressing torque ripples of permanent magnet synchronous motors[J].China Mechanical Engineering，2019，30（17）： 2084．

[6] 韩雪岩，刘文彬，朱龙飞.基于自抗扰的永磁同步电机附加谐波损耗抑制方法[J].电机与控制学报，2024，28（2）： 87.

HAN Xueyan，LIU Wenbin，ZHU Longfei．Suppression method of additional harmonic loss of permanent magnet synchronous motor based on active disturbance rejection technology [J]．Electric Machines and Control，2024，28（2）： 87．

[7] 陈哲，张序轩，刘春强，等. 基于比例谐振型自抗扰控制的永磁同步电机电流解耦及谐波抑制策略研究[J]. 中国电机工程学报，2022，42（24）： 9062.

CHEN Zhe，ZHANG Xuxuan，LIU Chunqiang，et al．Research on current decoupling and harmonic suppression strategy of permanent magnet synchronous motor based on proportional resonance type ADRC [J]．Proceedings of the CSEE，2022，42（24）： 9062．

[8] HUO J，ZHAO N，GAO R，et al．Torque ripple compensation with anti-overvoltage for electrolytic capacitorless PMSM compressor drives[J]．IEEE Journal of Emerging and Selected Topics in Power Electronics，2022，10（5）： 6148．

[9] WANG S，ZHANG G，WANG Q，et al．Torque disturbance compensation method based on adaptive fourier-transform for permanent magnet compressor drives[J]．IEEE Transactions on Power Electronics，2022，38（3）： 3612．

[10] LI M，XIAO H，CHENG M，et al．An adaptive strategy based on repetitive predictive control for improving adaptability of LCL-type grid-connected inverters under weak grid[J]．IEEE Transactions on Power Electronics，2022，37（3）： 2562.

[11] ELIOMAR R C D ， LUNARDI A ， FILHO A J S . Current control for DFIG systems under distorted voltage using predictive–repetitive control[J]．IEEE Journal of Emerging and Selected Topics in Power Electronics， 2021，9（4）： 4354．

[12] 张巧芬，刘彦呈，郭昊昊，等. 用于永磁同步电机周期性转速脉动抑制的重复控制[J]. 控制理论与应用，2022，39（3）： 432.

ZHANG Qiaofen，LIU Yancheng，GUO Haohao，et al．Repetitive control for periodic speed ripples suppression of permanent magnet synchronous motor [J]．Control Theory and Applications，2022，39（3）： 432．

[13] 付兴贺，顾胜东，何航，等. 基于新型串联内模扩张状态观测器的PMSM齿槽转矩补偿控制方法[J]. 中国电机工程学报，2022，42（23）： 8729.

FU Xinghe，GU Shengdong，HE Hang，et al．Compensation and rejection of cogging torque of PMSM based on novel internal model observer in series with extended state observer [J]．Proceedings of the CSEE，2022，42（23）： 8729．

[14] 仲宇翔，林鹤云，王激尧，等. 基于滑模控制的记忆电机调磁转速波动抑制[J]. 中国电机工程学报，2023，43（7）： 2512.

ZHONG Yuxiang，LIN Heyun，WANG Jiyao，et al．Speed variation suppression for memory machine during magnetization state manipulation based on sliding mode control[J]．Proceedings of the CSEE，2023，43（7）： 2512．

[15] 卜飞飞，郭子韬，顾毅君，等. 基于改进型降阶观测器的永磁直驱伺服电动机转矩扰动抑制策略[J]. 电工技术学报，2022，37（16）： 4104.

BU Feifei，GUO Zitao，GU Yijun，et al．Torque disturbance suppression strategy of permanent magnet direct drive servo motor based on improved reduced order observer [J]. Transactions of China Electrotechnical Society，2022，37（16）： 4104．

[16] WANG Y，GAO Y，ZHAO C，et al．Iterative learning based torque ripple suppression of flux-modulation double-stator machine[J]．IEEE Transactions on Industrial Electronics，2021，69（7）： 6645．

[17] BI G，ZHANG G，WANG G，et al．Adaptive iterative learning control-based rotor position harmonic error suppression method for sensorless PMSM drives[J]．IEEE Transactions on Industrial Electronics，2021，69（11）： 10870．

[18] HUANG M，DENG Y，LI H，et al．Torque ripple suppression of PMSM using fractional-order vector resonant and robust internal model control[J]．IEEE Transactions on Transportation Electrification，2021，7（3）： 1437．

[19] 曹荣敏，郑鑫鑫，侯忠生. 基于改进多入多出无模型自适应控制的二维直线电机迭代学习控制[J]. 电工技术学报，2021，36（19）： 4025.

CAO Rongmin，ZHENG Xinxin，HOU Zhongsheng．An iterative learning control based on improved multiple input and multiple output model free adaptive control for two-Dimensional linear motor[J]．Transactions of China Electrotechnical Society，2021，36（19）： 4025．

[20] 哀薇，胡林威，李向阳，等.基于自抗扰迭代学习控制的开关磁阻电机转矩脉动抑制[J].控制理论与应用，2020，37（10）： 2098.

AI Wei，HU Linwei，LI Xiangyang，et al．Active disturbance rejection based iterative learning control for torque ripple suppression in switched reluctance motor [J]．Control Theory and Applications，2020，37（10）： 2098.

[21] 孙灿．基于氮化镓功率器件的高速永磁同步电机驱动系统若干关键技术研究[D]．杭州：浙江大学，2022.

[22] AI Q，KE D，ZUO J，et al. High-order model-free adaptive iterative learning control of pneumatic artificial muscle with enhanced convergence[J]．IEEE Transactions on Industrial Electronics，2020，67（11）： 9548.

（编辑：邱赫男）