关于几何中多情况问题的讨论探究

[摘 要] 多情况讨论在几何问题中十分常见，探究解析时学生先需要确定问题类型，再结合对应方法分别构建模型求解. 学生具体求解时可采用数形结合的方法，提取其中的特殊图形和特殊关系，借助几何定理转化求解. 研究者通过开展问题综述，并结合实例分别探究，提出相应的教学建议.

[关键词] 多情况;分类讨论;等腰三角形;直角三角形

问题综述

1. 问题类型

多情况讨论问题在初中数学中十分常见，也常作为中考压轴题综合考查学生的解析思维. 多情况讨论问题的类型较为多样，分析对比主要可以细分为四种类型：

①关于等腰三角形存在性问题，主要讨论三角形腰的多情况;

②关于直角三角形存在性问题，主要讨论直角的多情况;

③关于特殊点、特殊位置的问题，主要讨论点位置的多情况;

④关于图形线段的问题，主要讨论线段位置的多情况.

2. 解题策略

对于多情况讨论问题，解题时学生需要对其中的几何要素进行解析讨论，必要时可以采用数形结合的方法，结合问题条件分别构建模型，利用模型来转化分析. 涉及点、线、图形变换等情形不确定时，学生可以采用如下分析思路.

点的直线位置不确定时，若点在AB上时，则可分为三种情形：①点在线段AB上;②点在线段AB的延长线上;③点在线段BA的延长线上.

点在三角形、四边形、抛物线上的位置不确定时，则需要对其在各边、各线段上的位置进行分别讨论，如点在四边形的对角线上时，则需要讨论两种情况;如点在抛物线上时，则需要对点在对称轴的左、右两侧进行讨论.

线段的位置不确定时，则需要结合线段的属性来分别讨论. 若线段为三角形的高，则需要讨论高在三角形的内部和三角形的外部两种情形;若涉及两条线段且为圆中的弦，则需要讨论三种情形：①一条弦经过圆心;②两条弦在圆心的同侧;③两条弦在圆心的异侧.

涉及图形变换方向不确定时，则需要对其方向进行分情况讨论. 如图形平移方向的讨论、图形旋转方向的讨论.

实例探究

上述对几何中的多情况问题的类型和解题策略进行了归纳总结. 教学中教师需要指导学生进行实例探究，构建解题思路，下面结合实例解析过程，总结思考.

1. 等腰三角形多情况讨论

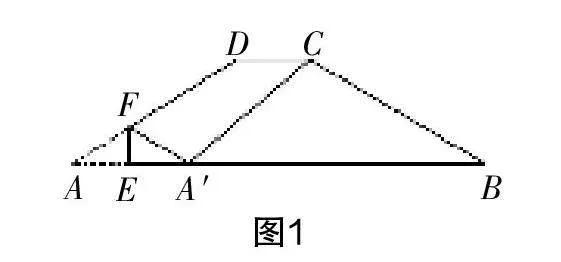
例1 如图1所示，在四边形纸片ABCD中，AB=12，CD=2，AD=BC=6，∠A=∠B. 现将纸片沿EF折叠，使点A的对应点A′落在AB边上，连接A′C. 若△A′BC恰好是以A′C为腰的等腰三角形，则AE的长为______.

分析：上述为等腰三角形多情况问题，虽然设定了A′C为腰，但依然存在两种情况：A′C=BC和A′C=A′B. 而在具体探究中，学生需要提取其中的特殊图形，讨论图形的具体情况. 后续针对等腰三角形的腰构建模型，分别讨论.

解析：过点C作CM⊥AB，设垂足为点M，再过点D作DN⊥AB，设垂足为点N.

因为AD=BC=6，∠A=∠B，∠DNA=∠CMB=90°，可证△ADN≌△BCM（AAS），由全等性质可得AN=BM，DN=CM. 又知DN∥CM，DN⊥AB，可证四边形DCMN是矩形，所以CD=MN=2，则AN=BM==5. 由题意可知将纸片沿着EF折叠，使得点A的对应点A′落在AB边上，可得AE=A′E.

①若A′C=BC，且CM⊥AB，如图2（1）所示，则BM=A′M=5，所以AA′=AB-A′B=12-10=2，可得AE=1.

②若A′C=A′B，过点A′作A′H⊥BC，如图2（2）所示. 由勾股定理可知CM2=BC2-BM2=A′C2-A′M2，代入线段长可求得A′B=，所以AA′=AB-A′B=，则AE=.

综上可知，AE的长为1或者.

评析 题目设定A′C为腰，故有两种情形，后续直接构建模型讨论即可. 解题的关键是作辅助线构建特殊图形矩形，推导出AN的长. 对等腰三角形的腰不确定问题，学生需要关注其中的设定条件，结合设定条件再确定不同的情形.

2. 直角三角形多情况讨论

例2 如图3所示，在矩形ABCD中，AB=6，BC=8，点E是对角线BD上一动点（不与点B、点D重合），将矩形沿过点E的直线MN折叠，使得点A、点B的对应点G、点F分别在直线AD与BC上，当△DEF为直角三角形时，CN的长为______.

分析：本题目为直角三角形多情况问题，涉及了矩形折叠，学生需要结合折叠特性，根据直角三角形特性来确定可能存在的情形. 由于点D为矩形的顶点，故△DEF为直角三角形时有两种情况：①∠DFE=90°;②∠EDF=90°. 后续构建模型提取其中的特殊图形来求解.

解析：当△DEF为直角三角形时，有如下两种情形.

①当∠DFE=90°时，△DEF为直角三角形，如图4（1）所示. 由于∠CDF+∠CFD=∠EFN+∠CFD=90°，所以∠CDF=∠EFN. 分析折叠过程，可得EF=EB，所以∠EFN=∠EBN，则∠CDF=∠CBD. 又因为∠DCF=∠BCD=90°，从而可证△DCF∽△BCD，由三角形相似性质可得=，即=，可求得CF=，所以FN=，可得CN=CF+NF=.

②当∠EDF=90°时，△DEF为直角三角形，如图4（2）所示. 由于∠CDF+∠CDB=∠CDB+∠CBD=90°，则∠CDF=∠CBD. 又知∠DCF=∠BCD=90°，可证△DCF∽△BCD，由三角形相似性质可得=，即=，可求得CF=，所以NF=，可得CN=NF-CF=.

综上可知，CN的长为或者.

评析 上述在解析直角三角形时，学生注意到点D为矩形的顶点，故不能以该点为直角顶点，从而将其细分为两种直角情形. 具体求解时，关键一步为提取其中的相似三角形，利用相似三角形的性质来构建线段长. 对于直角三角形的多情况讨论问题，需注意根据图形特征来确定可能存在的情形.

3. 特殊点、特殊位置多情况讨论

例3 如图5所示，在等边三角形ABC中，AB=4 cm，点M为边BC的中点，点N为边AB上的任意一点（不与点A、点B重合）. 若点B关于直线MN的对称点B′恰好落在等边△ABC的边上，则BN的长为______cm.

分析：本题目为关于特殊点、特殊位置的多情况讨论，点B关于直线MN的对称点B′恰好落在等边三角形ABC的边上，但其位置不确定，可有两种情形：①落在△ABC的边AB上，②落在△ABC的边AC上. 后续可分别构建模型，提取其中的特殊图形来求解.

解析：由于对称点B′恰好落在等边三角形ABC的边上，根据图形特征可知有如下两种情况：

①当点B关于直线MN的对称点B′恰好落在等边三角形ABC的边AB上时，则MN⊥AB，BN=B′N. 由于△ABC是等边三角形，则AB=AC=BC，∠ABC=60°. 由于点M为边BC的中点，所以BM=BC=AB=2，则BN=BM=1.

②当点B关于直线MN的对称点B′恰好落在等边三角形ABC的边AC上时，则MN⊥BB′，四边形BMB′N是菱形. 由于∠ABC=60°，点M为边BC的中点，所以BN=BM=BC=AB=2.

综上可知，BN的长为1 cm或者2 cm.

评析 上述讨论对称点的位置时分为了两种情况，其特殊之处为点在三角形的边上，故可直接确定点所在边的情形. 后续探究解析时学生充分利用等边三角形、轴对称的性质，结合菱形的性质来分析. 对于特殊点、特殊位置的多情况问题，学生要结合问题情形来确定具体的位置，尽量简化讨论情形，后续再构建模型.

4. 图形中线段的多情况讨论

例4 如图7所示，△ABC是一张等腰三角形纸片，且AB=AC=6，BC=4，将△ABC沿着某条过一个顶点的直线折叠，打开后再沿着所得到的折痕剪开，若剪开后的两个三角形能够拼成一个与原△ABC不全等的新三角形，则折痕的长为______.

分析：本题目分析剪切拼接后的三角形与原三角形不全等，进而求解线段长，实质上是关于线段的多情形讨论. 因折痕线段要过等腰三角形ABC的一个顶点，显然有两种情形：①过BC上的高;②过AC边上的中线.

解析：由于△ABC为等腰三角形，故折叠拼接有如下两种情形.

①过点A作AD⊥BC，设垂足为点D，如图8（1），此时沿着AD剪开后的两个三角形可以拼成一个与原△ABC不全等的新三角形.

由于AB=AC，则BD=CD=BC=2，在Rt△ABD中，由勾股定理可得AD==4.

②作AC上的中线BE，过点B作BH⊥AC，设垂足为点H，如图8（2），此时沿BE剪开后的两个三角形能够拼成一个与原△ABC不全等的新三角形.

设CH=x，则AH=6-x，由勾股定理可得BC2-CH2=AB2-AH2，代入线段可得42-x2=62-（6-x）2，可解得x=，所以BH=，可得EH=3-CH=，则由勾股定理可得BE==.

综上可知，折痕的长为4或.

评析 上述探究折叠拼接中的折痕长时，充分把握等腰三角形的特点，将其分为了两种情形：一是BC上的垂线;二是AC上的中线. 探究关于线段特殊位置的多情况问题，要充分利用其中的几何特性，提取模型，借助勾股定理、中线性质来推导求解线段长.

思考建议

几何中的多情况讨论是其中较为特殊的问题，学生在求解时很容易由于审题不严谨造成漏解或错解. 因此在探究教学中，教师要注意引导学生审题读题，把握题干的关键词，确定是否存在多情况，后续再根据总结的知识方法破解. 笔者提出以下几点建议：

一是归纳常见的多情况问题，从点、线、角、图形等视角进行总结，教学中引导学生关注等腰三角形腰的情形、直角三角形的直角顶点情形.

二是总结常见问题的破解方法，造成问题多情况的因素很多，但破题时总体上还是要落实到分析几何的点、线、图形中. 教学中教师要指导学生进行方法总结，如总结点在直线上的位置情形、线段位置不确定的讨论方法等.

三是渗透数形结合的分析方法，指导学生掌握该方法的构建思路，根据条件分别构建模型，再结合模型特征进行分析推导. 分析模型时注意提取其中的特殊图形，充分利用特殊图形和特殊关系来推导求解.