对提高初三复习课教学质量的策略研究

[摘 要] 在初三复习教学中，教师要更新教学观念，创新和改革课堂教学模式，结合教学实际制定教学策略，以此提升复习教学的质量，提高学生的能力，培养学生的素养. 在具体实施过程中，教师应树立“以生为本”的教学理念，结合教学内容和学生学情精心制定教学任务，并根据课堂生成进行有效的启发和指导，以此帮助学生夯实基础，突破难点，提升学习品质.

[关键词] 初三复习教学;教学观念;教学质量

根据新课标的要求，初中数学教学中，教师要充分发挥学生的主体价值，让学生学会用数学思维方式思考，增强学生发现、提出、分析和解决问题的能力. 在实际教学中，尤其在初三复习教学中，由于时间紧、任务重，为了完成教学任务，部分教师通过讲授的方式让学生理解数学知识，掌握解题方法. 但在此过程中，因为缺少学生独立思考和合作探究的过程，学生数学能力难以得到发展. 如何落实好新课标的要求，提高和发展学生的数学能力与数学素养呢？笔者结合教学实践谈谈初三复习的一些教学策略.

任务驱动，提升课堂活力

在传统复习教学中，部分教师在备课时会准备好思维导图，然后引导学生回顾定义、公式、概念等相关内容. 通过以上过程确实能够帮助学生完成知识的梳理，但是学生的思路往往被教师牵着走，学生容易出现消极的情绪，影响学习热情. 从课堂表现上来看，学生能够按照要求熟背概念、定理等内容，但是在应用时还是感觉束手无策，这样既浪费时间，又没有达到预期效果. 为了改变这一局面，教师不妨采用任务驱动的方式来完成，以此提高学生的积极性、主动性.

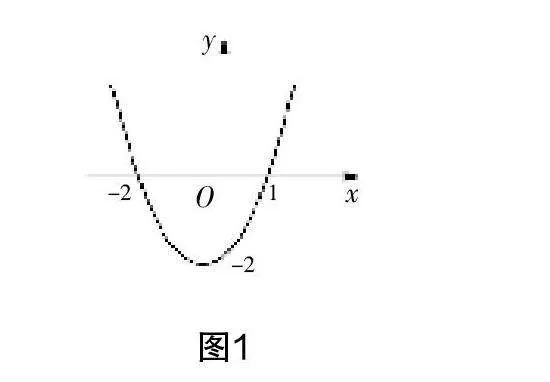
例如，在复习二次函数性质时，若在传统复习教学中，教师会给出二次函数的一般式，然后让学生说一说它的开口方向、对称轴、顶点坐标等. 传统教学模式虽然完成了知识的梳理，但是其理论解说过多，难免会让学生产生枯燥无味的感觉. 基于此，教师不妨设计如下任务：根据图1所示的抛物线可知这个二次函数的解析式是______，顶点坐标是______，对称轴是______，当x______时，y随x值的增大而减小，当x______时，y随x值的增大而增大. 借助任务驱动思考，既能帮助学生复习相关的知识点，又可以避免解说式复习的枯燥感，还锻炼了学生分析和解决问题的能力.

又如，在复习锐角三角函数时，教师在课上没有让学生背诵相关的概念，而是出示了如下任务：在Rt△ABC中，∠C=90°，a=6，b=3，则c=______，sinA=______，cosA=______，tanA=______，cotB=______. 通过任务的驱动，既帮助学生复习了锐角三角形的定义、锐角三角函数的定义、直角三角形三边的关系，又检测了学生对相关知识的掌握情况.

以生为本，激发学生的学习

动机

在初三复习教学中，教师时常遇到这样的困惑：对于一些基础题，若统一讲不仅会浪费宝贵的时间，还难以激发学优生的学习兴趣，但是不讲，有些学生依然存在问题. 面对这样的困惑，教师不妨发挥小组合作的优势，通过小组学习让学生相互帮扶，这样既能锻炼学优生的组织协调能力，又可以帮助学优生夯实基础，同时还能帮助学困生通过深层次的交流突破难点，增强学习信心. 另外，通过小组合作学习，可以充分发挥学生的主体价值.

例如，在复习等腰三角形相关知识时，教师出示了这样两道练习题：（1）在等腰三角形ABC中，AB=5，AC=9，求等腰三角形ABC的周长. （2）在等腰三角形ABC中，AB=4，AC=9，求等腰三角形ABC的周长. 以上两道题难度不大，但是很多学生在解题时还是出现了错误，出现错误的主要原因有以下两点：一是学生缺乏分类讨论意识;二是解题时忽视了三角形的三边关系. 为了让学生能够自主发现错误，并能主动解决问题，教师鼓励学生通过小组合作学习的方式来完成，通过调动学生参与活动的积极性，以加深学生对知识的理解，培养学生思维的严谨性.

问题暴露，提高反思能力

在传统复习教学中，教师会根据学生平时作业、考试反馈，以及自己的教学经验归纳总结一些重点和难点，然后采用重复讲、反复练的方式突出重点、突破难点. 采用这种模式确实能够起到一定的巩固和强化的作用，但是其中也会出现一些问题，比如通过重复讲、反复练，学生容易出现思维定式，表现为解题时生搬硬套;学生课上听清楚了、听明白了，在教师的带领下也顺利地解决了问题，但是在独自解题时依然束手无策，出现了“懂而不会”的情况;还有学生“坐享其成”，对教师产生了过度的依赖，影响自主学习能力的提升. 基于此，教师不妨将课堂交给学生，让没有顺利求解的学生讲思路、写过程，其他学生进行讲评，这样既能充分展示学生在学习中出现的问题，又能让学生在纠错和析错中加深对知识的理解，提高总结和反思的能力. 当学生充分暴露问题后，教师再进行针对性讲解，定能获得事半功倍的效果.

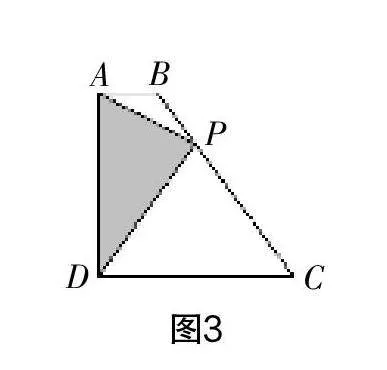
例如，在复习动点这一专题时，教师给出了这样一道题：如图3所示，在四边形ABCD中，AB∥CD，∠ADC=90°，点P从点A出发，以每秒1个单位的速度匀速运动，其运动路径为A→B→C→D. 设点P的运动时间为t秒，△ADP的面积为S，S关于t的函数图象如图4所示，当P运动到BC边的中点时，S=______.

动点问题一直是困扰学生的难点问题，也是中考的重要考点. 教师有必要通过专题训练的方式进行强化，以此帮助学生突破该难点. 本题将动点问题和函数问题有机地结合在一起，增加了问题的综合性，可以很好地考查学生的数学知识综合应用能力. 对于该题，解题的关键就是理解面积和时间的关系，弄清楚（6，8），（10，0）的实际意义. 如果能弄清楚这两点，学生就能读出以下信息：CD=4，当点P运动到C点时，△PAD的面积最大，其最大值为8，由此可知AD=4. 结合图4可知，当点P运动到B时，△PAD的面积为2，由此可知AB=1. 分析至此，结合梯形的中位线性质以及面积公式，问题迎刃而解.

在教学中，教师没有直接呈现解题过程，而是预留充足的时间让学生独立思考，从学生的解题反馈来看，很多学生因为没有理解题意，找不到解题的突破口. 在教学中，若教师仅呈现标准答案让学生独自理解，学生在学习中势必会出现“懂而不会”的情况，因此不妨先让没有解答出该题的学生谈谈自己的想法，充分暴露问题，然后由其他学生进行补充，最后由教师进行归纳和总结. 这样做可以充分发挥学生的主观能动性，有效规避定式思维和惰性思维的发生，切实提高学生的数学综合学习能力.

总之，在初三复习教学中，教师要提供时间和空间让学生思考、合作、交流，以此激活学生的思维，提高学生的学习能力，增强学生的学习信心，提升复习教学品质.