着眼全局谋发展 合作探究促落实

[摘 要] 促进学生核心素养发展是初中数学教学的基本导向. 在几何教学中，教师应从全局视角出发，教会学生几何研究方法，让学生学会学习. 在此过程中，教师应结合教学实际设计有效的实践探究活动，以此发展学生逻辑推理能力，培养学生抽象概括能力，提升学生数学核心素养.

[关键词] 全局视角;实践探究活动;数学核心素养

随着时代的进步，现代社会对人才的要求越来越高，数学作为基础学科，得到了人们的广泛关注. 数学课堂不仅要重视学生基础知识、基本技能和基本经验的培养，还要重视学生数学核心素养的培养. 教学中，教师应认真研究教材，着眼于整体，根据教学内容和学生实际学情设计问题情境，引导学生进行自主探究和合作交流，让学生既要明晰概念、定理等基础知识，又要掌握蕴含其中的数学思想和数学方法，以此提升学生数学核心素养.

笔者在教学“直线的相交”时，从学生已有经验出发，引导学生共同探寻知识形成过程，充分发挥学生的主体性，让学生在独立思考和合作探究中构建知识体系.

教学简录

1. 复习旧知，引入新知

师：几何是一门研究图形的形状、大小和位置关系的学科. 请大家回忆一下，我们现在已经学习了哪些几何图形呢？

生1：点、线、面.

生2：体. （学生补充）

师：很好，现在先看点，我们可以如何描述点与点的位置关系呢？

教师提示学生表达，学生互动交流，确定用“方向和距离”来描述点与点的位置关系.

师：怎样描述点与线之间的位置关系呢？

生3：点在直线上或点在直线外.

师：直线与直线存在怎么样的位置关系呢？

设计意图 教学初，教师从整体视角出发，给出“几何”的定义，让学生明晰几何研究的本质，培养学生全局意识. 教学中，教师引导学生回顾点与点和点与线的位置关系，自然引出本课研究的主题——直线与直线的位置关系.

2. 师生合作，探索新知

师：请大家动手画一画，想一想，两条直线存在怎样的位置关系呢？

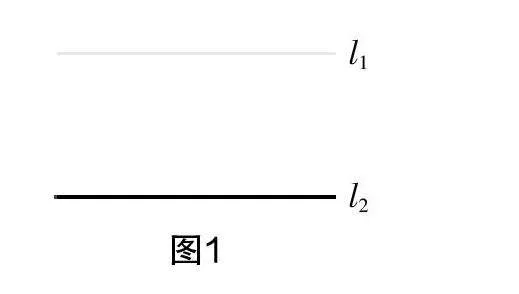
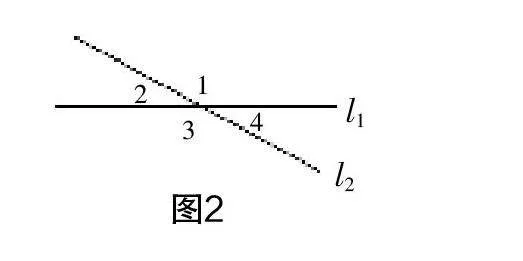
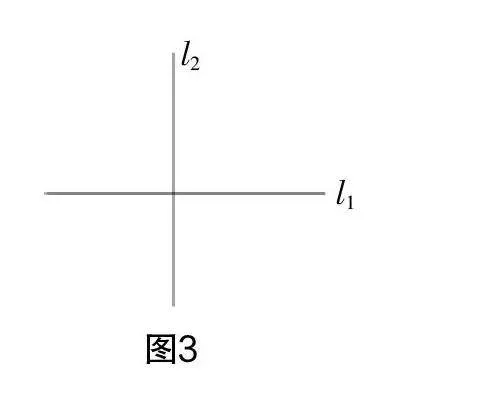
教师预留时间让学生动手画，然后进行组内交流，接下来教师投影展示学生作品，如图1、图2、图3.

师：如果两条直线不在同一平面内，还可能存在怎样的位置关系？（学生边思考边比画）

生4：不平行也不相交.

师：很好，今天我们重点先来研究平面内两条直线的位置关系，观察以上图形，请大家说一说，它们有什么共同点和不同点呢？（学生积极观察）

生5：共同点，都是两条直线，且两条直线在同一平面内;不同点，两条直线的交点个数不同，图1中两条直线没有交点，图2和图3中两条直线有1个交点.

师：总结得非常好，对于形如图2、图3这种只有一个交点，我们称两条直线相交，其公共点叫作这两条直线的交点. （教师板书）

师：图1这种不相交的情况我们后续研究，今天我们主要研究相交的直线. 请进一步观察图形，看看你还能找到其他相同点或不同点吗？（教师启发学生观察角）

生6：相同点是都有四个角;不同点是角的大小不一样.

师：这四个角有什么关系呢？（教师启发学生从顶点、边、位置关系等方面进行分析与交流）

生7：四个角有着公共顶点，该顶点即为两线的交点.

生8：四个角的边都在两条直线上，四个角相加等于360°.

师：非常好，大家发现了这么多秘密. 三个角会有怎样的关系呢？（学生继续思考）

生9：三个角除了有着相同的公共顶点，似乎也没有其他固定的数量关系.

师：没有固定的数量关系，看来我们没有研究三个角的必要. 这两个角之间存在怎样的关系？

为了便于研究，教师将图2中四个角进行标注.

师：现在请大家想一想，若将四个角两两组合，会出现几种组合呢？

生10：共有6种，分别为∠1与∠2，∠1与∠3，∠1与∠4，∠2与∠3，∠2与∠4，∠3与∠4.

师：很好，它们之间存在怎样的关系呢？我们先来看∠1与∠2.

生11：这两个角有相同的顶点，还有一条公共边.

生12：∠1+∠2=180°.

师：很好，我们将∠1与∠2这样的角称为邻补角.

接下来教师进一步解释邻补角，并给出邻补角的定义. （教师板书邻补角定义）

师：图2中还有哪些邻补角呢？

生13：∠1与∠4，∠2与∠3，∠3与∠4.

师：很好，接下来我们要研究哪组角了呢？

生：∠1与∠3，∠2与∠4.

师：很好，结合研究∠1与∠2的经验，说一说它们存在怎样的关系.

生14：它们有着相同的公共点，且角的两边互为反向延长线.

师：很好，像具有以上特征的角称为对顶角. （教师板书对顶角定义）

师：这样的角具有怎样的数量关系呢？

生15：∠1=∠3，∠2=∠4.

师：说一说你的理由.

生15：因为∠1+∠2=180°，∠2+∠3=180°，所以∠1=∠3. 同理可证∠2=∠4.

师：非常好，你能进一步进行归纳总结吗？

教师提供机会让学生总结归纳，从而得到“对顶角相等”这一重要性质.

设计意图 教学中，教师以探究为主线，引导学生从位置关系和数量关系两个层次进行深入的剖析，从而得到相关的定义及性质. 在此过程中，教师引导学生观察、分析、分类，促进了学生几何直观、抽象能力、推理能力等素养的提升.

3. 例题解析，深化新知

例1 如图2，∠1=130°，求∠2，∠3的度数.

问题给出后，教师让学生独立完成，学生根据邻补角互补求得∠2=50°，根据对顶角相等求得∠3=130°.

例2 如图2，已知∠1比∠2大80°，求∠3的度数.

例2难度略有提升，但是依然考查的是学生的基础知识掌握情况，学生通过列方程的方法很快求得∠1=130°. 又∠1=∠3，所以∠3=130°.

例3 如图2，若其中两个角的度数分别为（x+50）和（2x-10），则两条相交线形成的角分别是多少度？

教师先让学生独立思考，然后让学生简述自己的解答思路.

生16：题设中并未给出两角是对顶角还是邻补角，所以解题时需要分类讨论.

（1）若两角为对顶角，则有x+50=2x-10，即x=60，两条相交线形成的角的大小分别为110°、70°.

（2）若两角为邻补角，则有x+50+2x-10=180，即x=

°，两条相交线形成的角的大小分别为

°，

°.

例4 如图4，已知直线AD与BE相交于点O，∠DOE与∠COE互余，∠COE=62°，求∠AOB的度数.

师：谁来说一说你的解题思路？

生17：若想求∠AOB的度数，只要求∠DOE的度数，又∠DOE与∠COE互余，∠COE=62°，易得∠DOE=28°，所以∠AOB=28°.

设计意图 教师设计以上基础练习旨在进一步强化学生对对顶角、邻补角的定义及相关性质的理解，提高学生的分析和推理能力. 在此过程中，教师重视方程思想、分类讨论思想和转化思想的渗透，有效地培养了学生思维的严谨性和变通性，促进了学生解题能力的提升.

4. 课堂小结，内化新知

师：回顾本课学习内容，请大家从知识、方法、思想等方面进行归纳总结，谈谈你有哪些收获.

此环节教师让学生自主归纳总结，然后交流展示，以此逐渐丰富认知，促进知识的内化.

设计意图 通过课堂小结了解学生对知识、技能及方法的掌握情况，以便通过师生和生生的有效交流进一步完善学生的认知体系，最终让学生将知识内化为能力，为后续几何内容的学习打下坚实的基础.

教学思考

1. 关注数学知识体系的建构

在数学教学中，部分教师往往着眼于当堂教学内容的解决，忽视知识间的前后联系，使得学生的“学”缺乏系统性，不仅影响知识理解的深度，而且会加快遗忘的速度，这样学生在学习过程中很难提出自己的想法，只能被动接受，不利于学生培养数学核心素养. 在本课教学中，教师着眼于整体，让学生理解和掌握研究几何知识的方法，为后续研究三角形、四边形、圆等内容提供了方法保障，这样既可以提升学生举一反三能力，又能促进其对知识的理解及对几何知识体系的建构.

2. 关注数学思想方法的渗透

数学思想是数学教学的灵魂. 在课堂教学中，教师应重视引导学生挖掘蕴含其中的数学思想方法，让学生充分感知数学思想为学习带来的便利，培养终身学习能力. 在本课教学中，教师将无形的数学思想方法渗透于例题教学中，让学生充分体会学习分类讨论、方程、转化等数学思想方法的必要性和重要性，发展了学生的数学核心素养.

3. 关注数学推理能力的培养

在解决几何问题时，学习者有时从正向出发，根据知识条件推导所求结论;有时从逆向出发，根据所求结论，一步步向已知靠拢;也有时从正逆两个方向出发，推导所求结论. 无论从哪个角度出发，其都推动了学生数学推理能力的提升. 对于同一问题，若出发点不同，其推理过程也会有所不同，因此，教师应预留时间让学生去思考、去推理，主动探寻适合自己的解题方式，以此培养数学推理能力.

总之. 在几何教学中，教师不要拘泥于单一知识、单一问题的解决，应善于从整体的角度出发，用核心素养理论指导教学实践，以此让数学课堂更加饱满，更具质感，有效提升课堂教学品质，发展学生数学核心素养.