深度学习视域下的初中数学课堂教学实践探索

[摘 要] 深度学习是一种契合新课改背景的学习方式，为学科教学提供了导向. 研究者从深度学习的特征出发，以“反比例函数的图象与性质”的教学为例，着重引导学生经历“猜图—画图—悟图—赏图”的探究过程，以促使深度学习的发生.

[关键词] 深度学习;理解教学;反比例函数

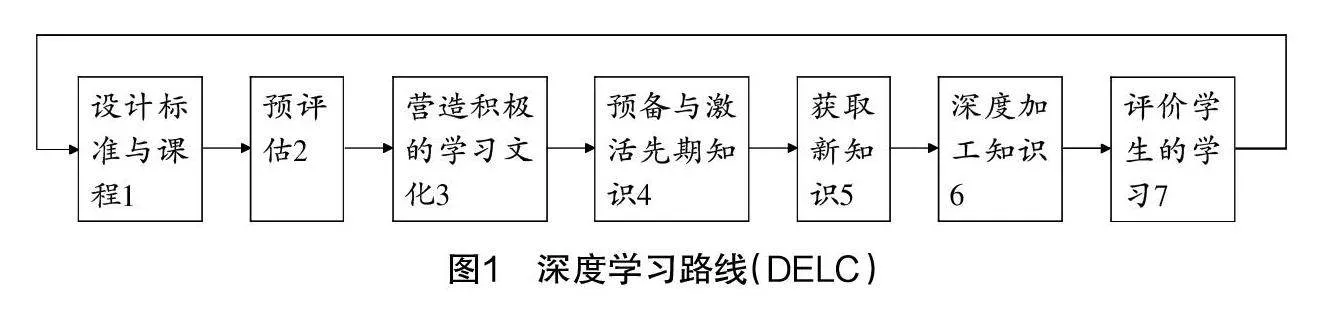
随着新课改的不断深入，深度学习为初中数学教育教学提供了新的导向. 美国学者Eric Jensen与LeAnn Nickelsen在《深度学习的7种有力策略》中提出了深度学习路线（DELC，The Deeper Learning Cycle）（见图1），对数学课堂教学具有指导意义. 本文以“反比例函数的图象与性质”为例，对基于深度学习的初中数学教学策略展开了实践与研究.

深度学习的特征

1. 深度学习属于理解性的学习

深度学习是相对于浅层学习而言的一种学习方式，相较于浅层学习的模式化、表面化，深度学习更强调对知识的理解性，需要学习者通过自主观察、分析、思考对所学内容产生疑问，从而批判性地理解知识本质，发现隐匿在知识背后的观念与思想. 学生在此过程中，不再是机械地记忆新知，而是在理解的基础上，带着自己的思维去建构新知.

2. 深度学习属于体系化的学习

浅层学习所建构的知识比较零碎，缺乏体系化，学生在应用时常因为思绪混乱而错误百出. 深度学习更注重知识的整体性与结构化，它是在学生已有的认知基础上，通过各种方法获取新知，形成新的知识体系的过程. 在此过程中，学生的认知不断得以优化，建立知识层级，使得基础知识在理解中沉淀，让学生学会从宏观的角度看待问题，同时不断补充、完善、拓展新知，扩大认知角度.

3. 深度学习是主动发生的学习

学习动机是学习的根本动力. 浅层学习的学习动机往往源自外部，不少学生是为了获得他人的认同而学习，但因为一些因素的影响就会减弱学习动机;深度学习更注重学生的终身可持续发展，其学习动机主要源自学习者的本身，因此这是一种有价值的学习，学生在学习过程中因不断获得良好的体验而形成良好的思维习惯.

教学分析

为了践行深度学习，笔者在备课时着重思考了如下两个问题：

思考一 学生的知识生长点在何处？

本节课之前，学生已经接触过了平面直角坐标系与一次函数有关的内容，对于坐标、一次函数、函数等有一定的认知基础，探索函数图象时积累了“列表、描点与连线”的基本方法. 鉴于知识存在正、负迁移两类情况，一些学生在画反比例函数图象时容易受思维定式的影响，因此引导学生深刻理解并感悟反比例函数的图象为平滑的双曲线是本节课教学的重点.

思考二 什么样的活动能深化学生对反比例函数图象的认识？

结合以往的教学经验，学生对于为什么反比例函数的图象是平滑的双曲线难以理解. 与一次函数探索方法进行类比，明确本节课探索的方法与方向：①由“数”出发猜想“形”，感知反比例函数的图象特征;②通过列表、描点与连线尝试自主画反比例函数的图象;③进行错例辨析，体会数形的一致性;④从特殊出发，总结图象的共性特征，明确反比例函数为平滑的双曲线;⑤感知反比例函数图象的美.

教学简录

1. 提出类比问题

问题1 一次函数的定义是什么，当时是怎样研究一次函数的？

问题2 与一次函数类比，本节课我们将会探索反比例函数的哪些方面？会用到什么方法进行探索？

设计意图 明确知识的生长点是践行深度学习理念的根本，鉴于学生已经有了探索一次函数的经验，反比例函数与一次函数属于一脉相承的关系. 由此可确定一次函数的研究方法就是反比例函数的知识生长点. 这种结合知识特点发展学生数学逻辑思维的教学方式，不仅能让学生进一步夯实知识基础，还能让学生通过学习方法的迁移获得自主探索新知的能力.

2. 开展探究活动

活动一 猜图

问题3 反比例函数y=的图象是什么？说明理由.

问题4 能否自主画出反比例函数y=的图象？设法验证其正确性.

设计意图 从学生认知“最近发展区”出发，鼓励学生根据式子来猜想图象，此为由数猜形的过程，属于数形结合思想的应用. 学生从式子出发自主尝试画图象，需思考该图象和坐标轴是否存在交点，图象在坐标系中位于哪个象限，呈现怎样的走势等. 这是揭露反比例函数图象本质的必经之路.

活动二 画图

问题5 怎样用“列表、描点、连线”的方法画出反比例函数y=的图象？

师生活动 列表环节，着重引导学生关注自变量的取值范围与所取值是否合理;描点环节，着重引导学生感知有序数对和坐标系内点的对应关系;画图环节，鼓励学生自主画图之后再交流，及时发现错误并纠正错误.

如图2，此为学生所画的典型错误图象.

问题6 （投影图2）该图象画得对不对？

学生经过独立思考、合作交流，对图2的画法进行正误的辨析，并说明错误的理由. 教师在此过程中进行适当引导，着重强调函数存在三种表达方式，想要辨别图2的画法的正误，关键在于回归到列表环节，从数与形两个维度出发进行思考与分析.

从“形”的角度来看，计算与描点方面可在列表时取x≠0的整数值，在描点后取相邻整数间的其他实数，比如在1和2之间取1.2或1.5等，那么y所对应的值就是5或4，即在点A（1，6）与点B（2，3）中间还存在点（1.2，5）与（1.5，4），如图3所示，实际描点后发现这两点并不位于线段AB上.

问题7 点A、点B之间还存在多少这样的点呢？其他任意两点间是否和点A、点B之间的情况一样呢？

为了深化学生的理解，让学生能直观地看到问题的本质，教师可借助几何画板进行描点操作，随着点个数的不断增加，平滑的曲线呈现出来.

从数的角度来看，图2是用线段将各个点进行了依次联结，显然这种方法是不科学的. 因此，笔者要求学生重新画反比例函数y=的图象，并分析所画图象与之前自己心中所想的图象是否一样.

设计意图 “用平滑的曲线来连线”为本节课教学的重点与难点，受一次函数图象画法的影响，不少学生在初次画图时会呈现出类似于图2的错误，利用好学生在课堂中的错误资源是促进深度学习的重要手段，学生的思维随着错例辨析的深入而清晰.

此过程，教师引导学生从“数、形”两个角度进行错因辨析，并借助几何画板展示从有限到无限，不仅让学生深刻理解了反比例函数的图象，还让学生进一步认识到知识迁移需要考虑周全，避免思维定式带来的负面影响. 随着探究的深入，学生不仅能自主画出反比例函数的图象，还进一步感知了图象的本质与“数形”的一致性，提炼了从有限到无限的数学思维，为促进深度学习的真实发生奠定了基础.

活动三 悟图

问题8 请自主画出反比例函数y=与y=-的图象，它们形态的异同点是什么？

问题9 若k发生变化，图象形态特征会不会随之发生改变？（借助几何画板探索）

设计意图 带领学生从特例出发进行画图、观察、分析与比较，鼓励学生自主发现反比例函数图象是由两个分支的平滑曲线组成，虽然无限趋近坐标轴，却不会与坐标轴相交. 几何画板的直观性，让学生进一步感知结论的合理性，并从中提炼由特殊到一般的数学思想方法.

活动四 赏图

问题10 反比例函数的双曲线带给你什么感受？

学生一致认为平滑的双曲线给人一种美的享受，反比例函数图象具有特别的平滑美、简约美、对称美等.

随着赞颂声，本节课的教学也接近尾声，教师可在此时带领学生对本节课进行整体性的回顾与总结，对研究方式方法、重点难点、涉及的数学思想方法等进行归纳.

设计意图 数学美的体验是践行新课标要求的过程，这种以美激趣的方法不仅能陶冶学生的情操，增强学生对数学学习的兴趣，还能提高学生的个人修养，赋予双曲线以独特的生命，让深度学习在学生良好的感悟中发生.

教学思考

1. 深度学习需理解数学本质

“知识的宽度、深度以及思维的高度”是构成深度学习的三个维度，实践证明所谓的深度学习并非是线性发展的过程，而应是三维立体逐渐深化的过程. 章建跃提出“三个理解”的理念，即理解数学、理解学生、理解教学. 一线数学教师首先要理解数学，即对知识的生长点、本质、内涵等有明确的认识，如知识的形成背景、逻辑发展规律与蕴含的数学思想方法等要一清二楚.

教师在一次函数的基础上类比教学本节课，通过对知识生长点的剖析，带领学生在类比分析中深刻认识什么是反比例函数，它具备怎样的特征与逻辑发展规律等. 反比例函数图象的探究是本节课教学的重点与难点，因此笔者由始至终借助反比例函数y=的图象探索设计活动，引导学生经历“猜图—画图—悟图—赏图”的过程，让学生对反比例函数的图象为什么是平滑的双曲线产生深刻理解.

在对图象的探索过程中，学生切身体会了数形结合思想、特殊到一般的数学思想方法等，尤其是几何画板的介入，让抽象的数学知识变得更加直观，有效发展了学生的抽象素养与直观想象力，这些都是践行深度学习的基础.

2. 深度学习需关注学生的认知发展

对学生认知发展的预设与评估是实现深度学习不可或缺的环节，教师作为课堂的组织者，需思考如何让学生完成自主建构，怎样将所学知识转化成个人能力等. 澳大利亚的John Biggs作为深度学习的资深学者，他认为学生在学习新知之前的知识、智力、能力、家庭背景与个性是影响深度学习的主要因素. 同时，学习环境等是影响深度学习的另一重要因素（见图4）. 因此，教师在预设与评估方面需着重关注学生原有的认知.

笔者在“John Biggs深度学习的3P模型”基础上对本节课的教学进行了思考，分别从“知识的生长点”与“如何设计探究活动”两个方面对课堂进行了预设与评估，取得了不错的教学成效.

3. 深度学习离不开问题导向

问题是推进教学的灵魂，想要让学生积极主动地参与探究活动，离不开任务的驱动. 而任务的驱动往往隐藏在一个个的问题中，合理的问题可有效激发学生学习的主观能动性，让学生的思维有明确的方向，这也是激活课堂的重要方法.

一环接一环的问题是派发给学生的指令，学生在问题的导向下深受启发. 本节课中，学生在十个问题的启发下，自主探索反比例函数的概念与图象，对图象的画法、易错点进行了辨析，从根本上掌握了反比例函数图象的本质，实现了深度学习.

总之，新课标背景下的数学教学应将“三个理解”放在首位，教师可结合学情与教情从对知识的关注转化成对学力发展的关注，从对结果的关注转化到对教学过程的关注，这是培养创新人才的关键，更是践行深度学习的重要方法.