家长数学教育观念与幼儿数学过程性能力的关系：亲子数学活动的中介作用

*基金项目：浙江省省级课程思政项目“学前儿童数学教育”、浙江省教研重点课题“幼儿园表现性评价赋能园所质量的行动研究”（编号：21gzz05）

**通信作者：李娟，温州大学教育学院教授，博士，硕士生导师

［摘 要］ 家长数学教育观念与亲子数学活动对幼儿数学过程性能力的发展有非常重要的影响。为讨论家长数学教育观念、亲子数学活动、幼儿数学过程性能力三者之间的关系，本研究从浙江省W市3所幼儿园抽取280名大班幼儿及父母作为被试，采用家长数学教育观念量表、亲子数学活动问卷和幼儿数学过程性能力检核表来考察家长数学教育观念和亲子数学活动对幼儿数学过程性能力发展的影响，并分析亲子数学活动的中介作用。结果显示，家长数学教育观念、亲子数学活动和幼儿数学过程性能力基本处于中等水平。家长数学教育观念、亲子数学活动和幼儿数学过程性能力三者之间呈显著正相关关系。家长数学教育观念和亲子数学活动均能显著正向预测幼儿数学过程性能力的发展。亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间起部分中介作用，其中：示范式教导对幼儿数学推理与验证能力以及数学关联能力起完全中介作用；对话式教导对幼儿数学关联能力起完全中介作用；游戏式教导对幼儿数学推理与验证能力起部分中介作用，对数学关联能力起完全中介作用；直接式教导的中介效应不显著。家长可从树立建构型教育观念、提高亲子活动水平、采用不同亲子活动方式、重视幼儿非智力因素等方面来发展幼儿的数学过程性能力。

［关键词］ 家长数学教育观念；数学过程性能力；亲子数学活动

一、问题提出

幼儿数学过程性能力是指幼儿理解和运用数学知识的能力，[1]具体包括数学交流、数学表征、数学推理与验证以及数学关联四个方面。[2]数学过程性能力不仅是数学素养的重要组成部分，对幼儿的数学学习至关重要，还是个体终身学习能力和创新实践能力的核心。《3～6岁儿童学习与发展指南》中对数学认知领域虽没有明确提出数学过程性能力，但是在子目标中提到的“理解数与数之间的关系”“解决生活中的问题”等都与数学过程性能力密切相关。大量的实证研究指出，良好的数学过程性能力对幼儿的问题解决能力[3]、理解力[4]、创造力和自我效能感[5]、数学成绩[6]以及日后的学业成就等方面的发展均具有积极影响。然而，我国对幼儿数学过程性能力的政策导向不够突出，关注不够充分，也缺乏相关的实证研究。因此，为了提高人们对幼儿数学过程性能力的重视，促进幼儿数学高阶思维的发展，探讨幼儿数学过程性能力的影响因素及影响机制尤为重要。

梳理已有文献发现，家庭因素是影响幼儿数学学习的重要因素之一，[7]家庭因素中的家长数学教育观念[8]、亲子数学活动[9]、家庭社会经济地位[10]、家庭文化资本[11]、数学谈话频率[12]、家长参与程度[13]和父母教养方式[14]等都会对幼儿数学学习能力的发展产生影响。其中，家长数学教育观念对幼儿的数学学习的影响更为深远。家长数学教育观念是指家长对如何进行数学教育以及幼儿如何学习数学的理念与看法，具体包括幼儿数学学习观和幼儿数学教导观两个维度。[15]已有研究表明，家长数学教育观念对儿童数概念的发展[16]、数学学习成绩[17]、数学学习能力[18]以及未来学业成就[19]等方面均有影响，而幼儿数学能力的发展也会对家长的数学教育观念产生影响，幼儿数学能力发展得越好，家长就会越重视幼儿的数学学习。[20]还有研究指出，家长教育观念不仅是影响幼儿发展的直接因素，它还可以通过影响家长的教育行为、教养方式来间接促进幼儿的发展，而亲子数学活动能更多地体现家长的教育行为、教养方式和参与情况。亲子数学活动是指在家长与幼儿之间进行的与数学学习有关的活动。[21]另有研究指出，家庭中存在着大量的亲子数学活动。[22]在幼儿期，将亲子数学活动有意或无意地融入幼儿的一日生活当中，不仅能够激发幼儿对数学学习的兴趣与好奇心，还能提高其早期数学能力。[23][24]

家长数学教育观念和亲子数学活动都会影响幼儿数学能力的发展，但是家长数学教育观念、亲子数学活动和幼儿数学过程性能力三者之间是否存在关系及其作用路径如何，尚无研究对此进行全面的考察。弗斯坦（R. Feuerstein）的中介学习经验理论（The Theory of Mediated Learning Experience，MLE）指出，儿童的认知结构主要通过两种方式与环境相互作用而得到发展：一种是直接与环境接触的直接学习，另一种是中介学习。中介学习是人类特有的学习方式。在这一学习形式中，由环境所发出的刺激信息被中介所转换，中介在注意、文化、情绪、经验等因素的影响下被儿童选择和组织刺激，在交互作用中促进儿童认知结构的发展。[25]结合中介学习经验理论，幼儿的数学学习是一种中介学习，是一种有目的、有挑战性的活动。家长会在与幼儿互动之前对相关的数学内容进行策划、组织或安排，持有不同数学教育观念的家长会选择不同的亲子数学互动方式，进而对幼儿数学能力的发展产生不同的影响。

鉴于此，本研究基于中介学习经验理论，选取大班幼儿及父母为研究对象，在深入了解家长数学教育观念、亲子数学活动和幼儿数学过程性能力现状的基础上，尝试构建家长数学教育观念影响幼儿数学过程性能力发展的中介模型，以期从家庭教育的角度为改善家长数学教育观念、提高亲子数学活动水平、加强家长对幼儿数学过程性能力发展的支持提供依据。本研究提出以下家长数学教育观念如何影响幼儿数学过程性能力发展的模型，主要探讨以下两个问题：（1）家长数学教育观念对幼儿数学过程性能力的影响；（2）亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间的中介作用。（见图1）

■

图1 家长数学教育观念、亲子数学活动和幼儿数学过程性能力之间的关系模型图

二、研究方法

（一）研究对象

本研究选取浙江省W市一所一级公办园和两所二级公办园共14个班为样本，采取幼儿与家长一一对应的方法，根据随机抽取的幼儿名单来确定家长样本。研究共选择280名大班幼儿及其家长为研究对象。（见表1）

表1 被试情况一览表（N=280）

■

续表

■注：依据张瑞峰的研究，本研究把照顾孩子的主要方式分为六类[26]：一类，一直由孩子的父母独自照顾；二类，由孩子父母和保姆共同照顾；三类，三代同住，由父母和祖辈共同照顾；四类，白天放在祖辈家，晚上接回父母家；五类，一直放在祖辈家，偶尔接回父母家；六类，其他（主要为和祖辈不同住，但祖辈有帮忙照顾）。依据师保国和申继亮的研究，本研究把家长职业分为六类[27]：一类，临时工、失业人员、待业人员、非技术及农业劳动者阶层（如农民）；二类，体力劳动工人、个体经营人员、技术工及同级工作者（如建筑工人及相关人员）；三类，一般管理人员与一般专业技术人员、事务性工作人员（包括商业服务业员工阶层、办事人员阶层，如售货员、司机等）；四类，中层管理人员与中级专业技术人员、助理专业人员，包括在各种经济成分的机构（如国家机关、党群组织、全民企事业单位、集体企事业单位和各类非公有制经济企业）中专门从事各种专业性工作和科学技术工作的人员，如教师、医生、技师等；五类，职业高级管理人员与高级专业技术人员、专业主管人员，包括在党政、事业和社会团体机关单位中行使实际行政管理职权的领导干部、大中型企业中非业主身份的中高层管理人员或私营企业主阶层，如公务员、公司经理等；六类，其他。

（二）研究工具

1. 家长数学教育观念量表。

本研究采用台湾学者林惠雅编制、黄瑾和程祁修订的家长数学教育观念量表，[28]对家长数学教育观念进行考察。该工具主要从家长的幼儿数学学习观和幼儿数学教导观两个方面来考察家长的数学教育观念，具体分为幼儿数学学习角色、幼儿数学学习历程、家长教导角色和家长教导历程四个维度。在问题的设计上，本研究分别依据传统和建构主义的观点来进行表述，将教育观念区分为偏向传统或偏向建构的观点，从而考察家长数学教育观念的基本取向。在本研究中，每一个层面的观点取向并不是绝对二分的，只是偏向程度不同。基于此，本研究将家长数学教育观念具体划分为建构教导历程观、传统教导历程观、建构知识学习观和传统知识学习观四个维度共20个子项目。其中建构教导历程观是指家长在对幼儿数学学习进行教导时更多地强调幼儿的能力，借由提供问题解决及探索的机会来促进幼儿的学习，鼓励幼儿思考，家长起的作用是引导和促进。传统教导历程观是指家长在对幼儿数学学习进行教导时更多地强调对幼儿灌输知识，认为教导中应多提供题目让幼儿反复练习，家长起的作用是教导和监督。持建构知识学习观的家长会认为幼儿的数学学习主要靠幼儿自身的操作和探索，注重对数学知识的理解和应用。持传统知识学习观的家长会认为幼儿学习数学主要靠学习者之外的因素，尤其是老师或家长的教导，且幼儿的学习主要靠记忆和背诵。该量表由家长进行评定，采用李克特（Likert Type）5点计分法，从1（非常不同意）到5（非常同意），得分越高表明该维度上的家长数学教育观念越趋向建构主义的观点，其中1、2、5、7、8、9、10、15、17为反向计分题。本研究中该量表的Cronbach’s α系数为0.70，其中建构教导历程观、传统教导历程观、建构知识学习观和传统知识学习观四个维度对应的Cronbach’s α系数分别为0.833、0.828、0.766和0.754。有学者认为，如果α系数大于0.80，则内部一致性较高。[29]有些学者则指出，α系数在0.70以上即为可接受的最小信度值。[30]在探索性研究中，信度最低标准是α系数在0.50以上，0.60以上为较佳。[31]因此，家长数学教育观念量表在本研究中具有较好的信效度。

2. 亲子数学活动问卷。

本研究采用Jong编制、黄瑾和程祁修订的亲子数学活动问卷，[32]对父母的亲子数学活动进行考察。该量表涉及示范示教导、对话式教导、游戏式教导和直接式教导四个维度共23个子项目。其中，对话式教导主要指家长采取问答、解释或告知等方式来支持幼儿的数学学习，游戏式教导主要指家长采取游戏、娱乐活动等方式来支持幼儿的数学学习，直接式教导主要指家长采取直接教导的方式来支持幼儿的数学学习，示范式教导主要指家长采取举例说明或利用实物等方式来支持幼儿的数学学习。虽然在实际的亲子数学活动中，家长的某一行为可能会具备两种或两种以上教导方式的特征，但该问卷主要根据这四种教导方式的定义来判断某一行为体现哪种教导方式的特性更多，就将其归为哪一类。例如，“我会跟孩子一起念唱有关数的儿歌”这一行为包含了家长和儿童的数学语言，同时也是一种以语言为材料的游戏，那么它到底归为对话式教导还是游戏式教导呢？对话式教导更强调幼儿与成人之间的对话与交流，突出亲子数学活动过程中数学语言多回合的输入与输出，而游戏式教导往往具有想象和假装等特点，更强调趣味性、自主性、情景性和体验性。本指标体系并没有凸显亲子间多回合的对话，而更多体现了对语言的嬉戏性运用，符合以语言为材料的游戏的特点，因此将其归为游戏式教导。

还需要说明的是，对照四种教导方式的定义，本研究发现原有问卷个别指标有归类不清的问题。因此，研究者基于专家意见（2名学前教育专业博士、教授，1名学前教育专业博士、副教授），在与问卷开发者讨论的基础上，对个别指标的归类进行了调整。其中示范式教导中的第13题“我教孩子数数1、2、3、4、5……”划归为直接式教导，因为这一题更多体现了家长直接教孩子数学知识这一特点；第23题“我会和孩子讨论他/她衣服上的颜色”划归为对话式教导，因为讨论更多体现了亲子之间的对话与交流。对话式教导中的第9题“我会让孩子分类整理自己的玩具”和第17题“我让孩子帮我量米量水”划归为游戏式教导，因为根据刘焱等人的观点，[33]“整理玩具”和“量米量水”是由“拿、放”“盛、运”等简单且重复的动作构成的，符合练习性游戏的特点。

该量表由家长进行评定，采用李克特（Likert Type）5点计分法，从1（从未做）到5（每天做），得分越高表示家庭的亲子数学活动频率越高。本研究中该量表的Cronbach’s α系数为0.913，其中示范式教导、对话式教导、直接式教导和游戏式教导四个维度的Cronbach’s α系数分别为0.810、0.803、0.744和0.734。因此，亲子数学活动问卷在本研究中具有较好的信效度。

3. 幼儿数学过程性能力量表。

本研究采用周晶和郭力平编制的5～7岁儿童数学过程性能力检核表[34]来测查幼儿的数学过程性能力。该量表主要包括数学交流能力、数学表征能力、数学推理与验证能力和数学关联能力四个维度共18个子项目，由研究者根据现场提问、儿童书写答案以及录制视频进行数据收集，采用三分制评分法对幼儿的回答进行打分，从0（不正确）到2（完全正确），得分越高表示幼儿的数学过程性能力发展越好。本研究中该量表的Cronbach’s α系数为0.775。

（三）研究过程

首先，在获得幼儿园教师及家长的同意后，利用幼儿园自由活动时间，研究者对共计280名大班幼儿的数学过程性能力进行测查。研究采用小组施测的方式进行“10的分解与组合”活动，每5名儿童为一组，每组测试时间为30分钟左右。活动分为三个环节，即教师提问、儿童操作和集体讨论，并对整个环节进行录像。其次，在测查一周后，由班主任在家长群里采取线上调研的形式发放问卷，并向家长介绍问卷填写的注意事项，强调问卷填写的真实性和匿名性，并由孩子的主要辅导者进行填写。

（四）数据处理

本研究采用SPSS 26.0统计软件对所有数据进行校对核查，并对收集到的数据进行描述性统计、独立样本t检验、单因素方差分析、相关分析、回归分析，并用SPSS？鄄PROCESS 插件进行Bootstrap方法检验亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间的中介作用。

三、研究结果与分析

（一）家长数学教育观念、亲子数学活动与幼儿数学过程性能力的现状分析

本研究以平均数、标准差等描述性统计分析的方法对家长数学教育观念、亲子数学活动和幼儿数学过程性能力进行探查。（见表2）

表2 各变量的描述统计

■

结果显示，家长数学教育观念整体均分为3.37，略高于3分，表明本研究中家长数学教育观念的基本取向略倾向于建构主义的观点。亲子数学活动整体均分为3.00，表明本研究中的大多数家庭能够为幼儿提供一定的亲子数学活动，其中示范式教导得分最高，游戏式教导得分最低，也就是说在亲子数学活动过程中，家长运用最多的互动方式是示范，而游戏互动最少。幼儿数学过程性能力整体均分为1.12，发生频率介于“明白但不完全正确”和“完全正确”之间，表明本研究中大部分幼儿的数学过程性能力处于中等偏上一点的水平，即大多数幼儿的回答情况能够表明幼儿对问题的理解，但是不能做出完全正确的解释。本研究进一步对家长数学教育观念、亲子数学活动与幼儿数学过程性能力在人口学变量上的差异进行了检验，结果显示：家长数学教育观念在园所等级、家庭年收入、父母学历、父母职业上存在显著差异；亲子数学活动在家长年龄、家庭年收入、父母学历、父亲职业上存在显著差异；幼儿数学过程性能力在家庭年收入、父亲学历上存在显著差异。

（二）家长数学教育观念、亲子数学活动与幼儿数学过程性能力的相关分析

本研究采用皮尔逊（Pearson）相关分析对家长数学教育观念、亲子数学活动与幼儿数学过程性能力的总体维度得分进行检验。（见表3）

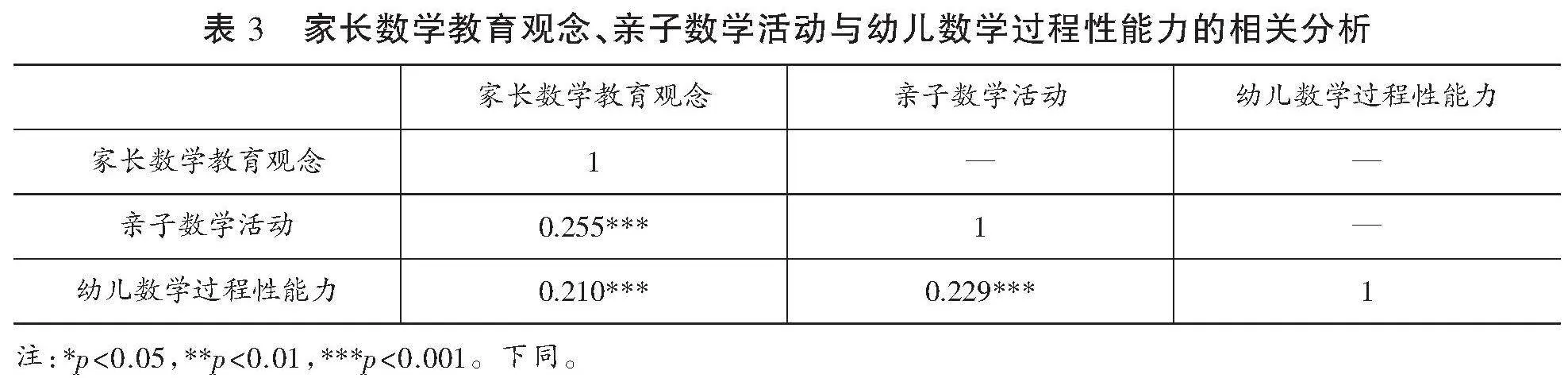
表3 家长数学教育观念、亲子数学活动与幼儿数学过程性能力的相关分析

■

注：*p<0.05，**p<0.01，***p<0.001。下同。

结果显示：家长数学教育观念与幼儿数学过程性能力呈显著正相关（r=0.210***，p<0.001）；亲子数学活动与幼儿数学过程性能力呈显著正相关（r=0.229***，p<0.001）；家长数学教育观念与亲子数学活动呈显著正相关（r=0.255***，p<0.001）。

（三）家长数学教育观念对幼儿数学过程性能力的直接预测效应

以家长数学教育观念总体为预测变量，幼儿数学过程性能力为结果变量，采用线性回归检验家长数学教育观念对幼儿数学过程性能力的直接效应。由于家庭年收入和父亲学历是影响幼儿数学过程性能力的人口学变量，因此需要将二者纳入控制变量，随后把幼儿数学过程性能力总体作为因变量，最后将家长数学教育观念总体作为自变量放入。（见表4）由于家长数学教育观念中的建构教导历程观和传统知识学习观与幼儿数学交流能力存在显著相关，为进一步探索二者对幼儿数学交流能力的影响，本研究以这二者为预测变量，以幼儿数学交流能力为效果变量，进行线性回归分析。结果显示，家长的建构教导历程观可以显著预测幼儿的数学交流能力，而家长的传统知识学习观不能显著预测幼儿的数学交流能力。（见表5）

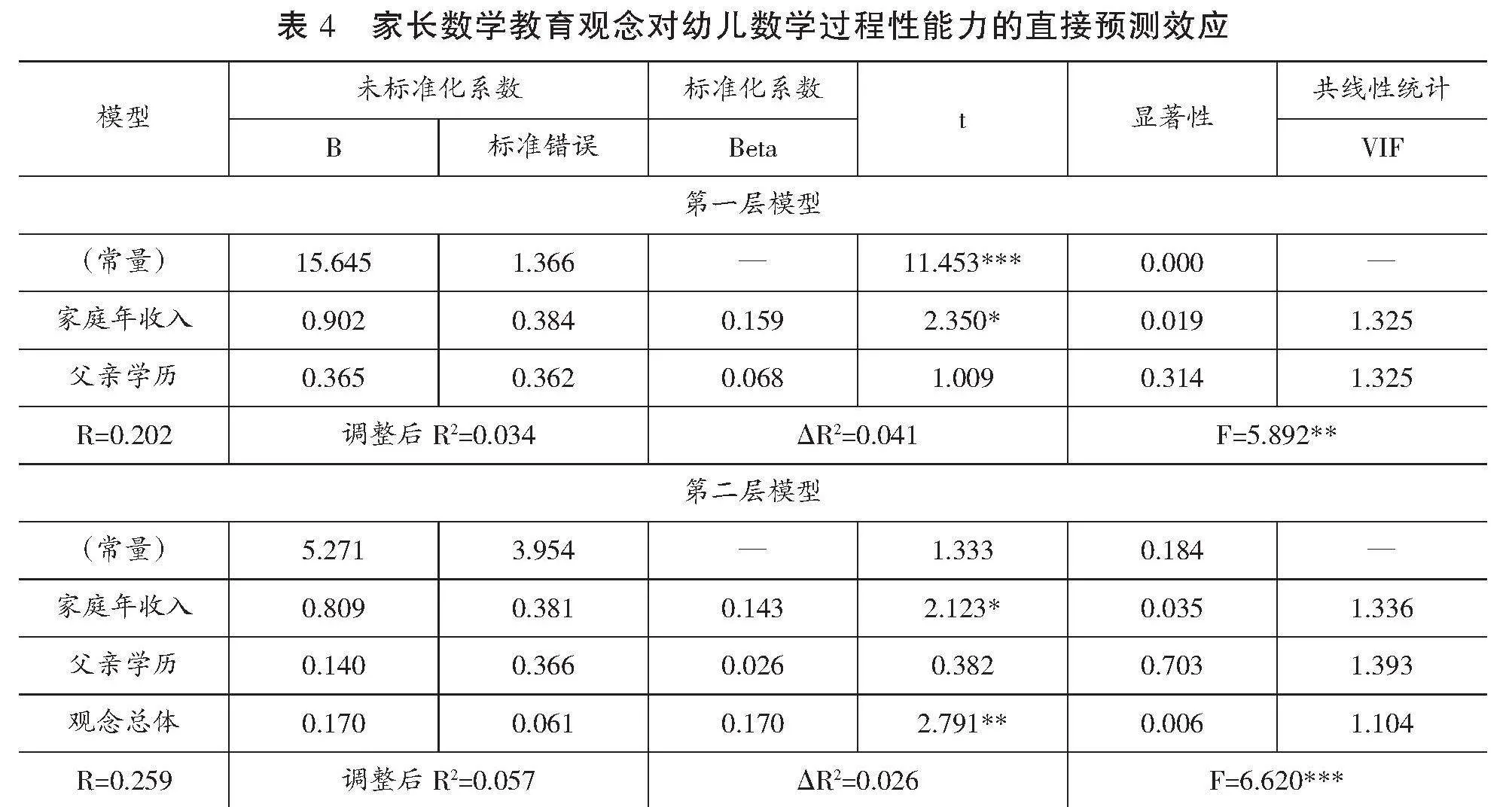
表4 家长数学教育观念对幼儿数学过程性能力的直接预测效应

■

根据表4的统计结果，自变量之间不存在多重共线性（VIF<5），意味着本次结果运算准确可靠。在控制了家庭年收入与父亲学历之后，整体模型有统计学意义上的显著差异，F=6.620，p<0.001，调整后R2=0.057，ΔR2=0.026。家长数学教育观念对幼儿数学过程性能力有显著的正向预测作用。

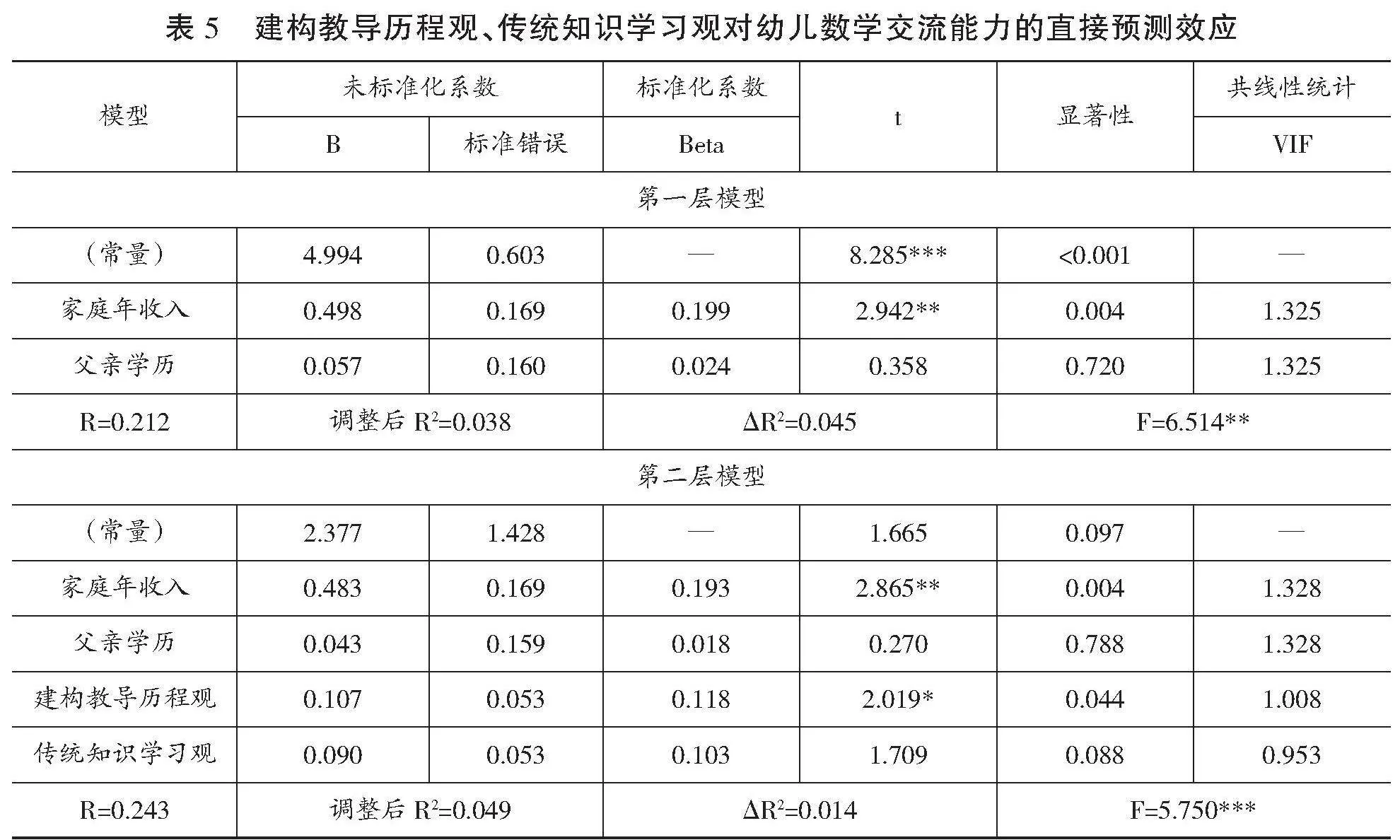
表5 建构教导历程观、传统知识学习观对幼儿数学交流能力的直接预测效应

■

根据表5的统计结果，自变量之间不存在多重共线性（VIF<5），意味着本次结果运算准确可靠。在控制了家庭年收入与父亲学历之后，整体模型有统计学意义上的显著差异，F=5.750，p<0.001，调整后R2=0.049，ΔR2=0.014。家长的建构教导历程观对幼儿数学交流能力有显著的正向预测作用，而家长的传统知识学习观对幼儿的数学交流能力没有显著预测作用，也就是说持有建构教导历程观的家长在对幼儿数学进行教导时，会更注重引导和促进幼儿的数学交流能力的发展。

（四）亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间的整体中介效应

上述结果表明，家长数学教育观念、亲子数学活动和幼儿数学过程性能力两两之间存在显著正相关，且家长数学教育观念可以显著正向预测幼儿数学过程性能力，因此可以进行下一步的中介效应检验。采用海耶斯（Hayes）编制的SPSS？鄄PROCESS插件对亲子数学活动在家长数学教育观念作用于幼儿数学过程性能力的中介效应进行检验。检验模型选择Model 4，并采用偏差校正的百分位Bootstrap方法（重复抽样5 000次）对回归系数的显著性进行检验。（见表6、表7）

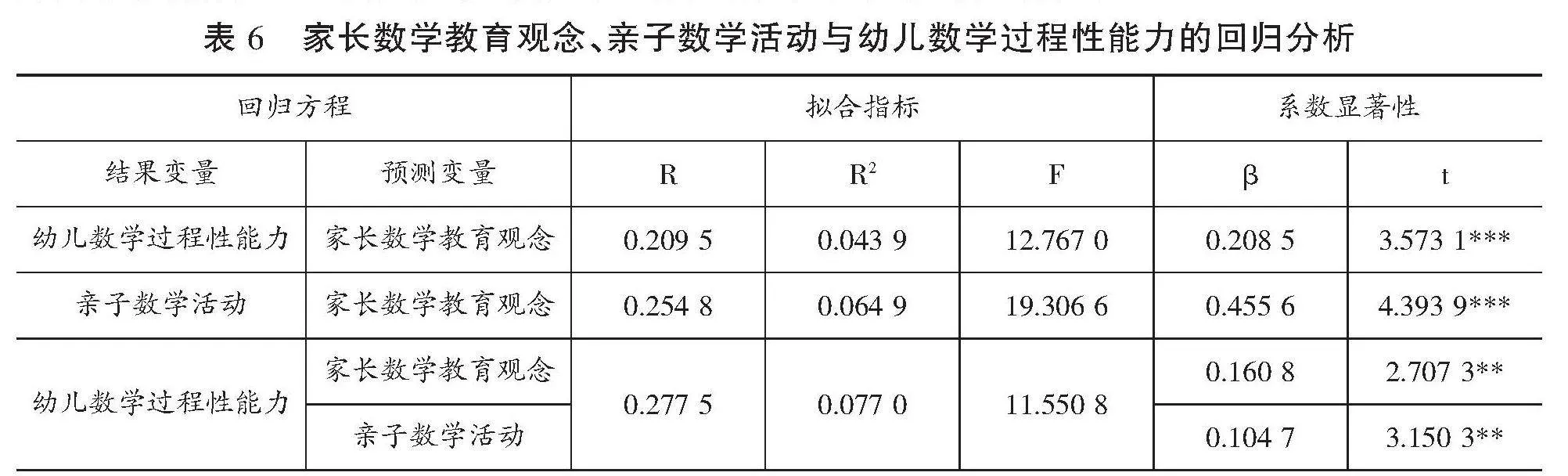
表6 家长数学教育观念、亲子数学活动与幼儿数学过程性能力的回归分析

■

结果显示，家长数学教育观念对幼儿数学过程性能力的预测作用显著（β=0.208 5，t=3.573 1，p＜0.001），且当放入中介变量后，家长数学教育观念对幼儿数学过程性能力的直接预测作用依然显著（β=0.160 8，t=2.707 3，p＜0.01）。家长数学教育观念对亲子数学活动的正向预测作用显著（β=0.455 6，t=4.393 9，p＜0.001），亲子数学活动对幼儿数学过程性能力的正向预测作用也显著（β=0.104 7，t=3.150 3，p＜0.01）。（见表6）

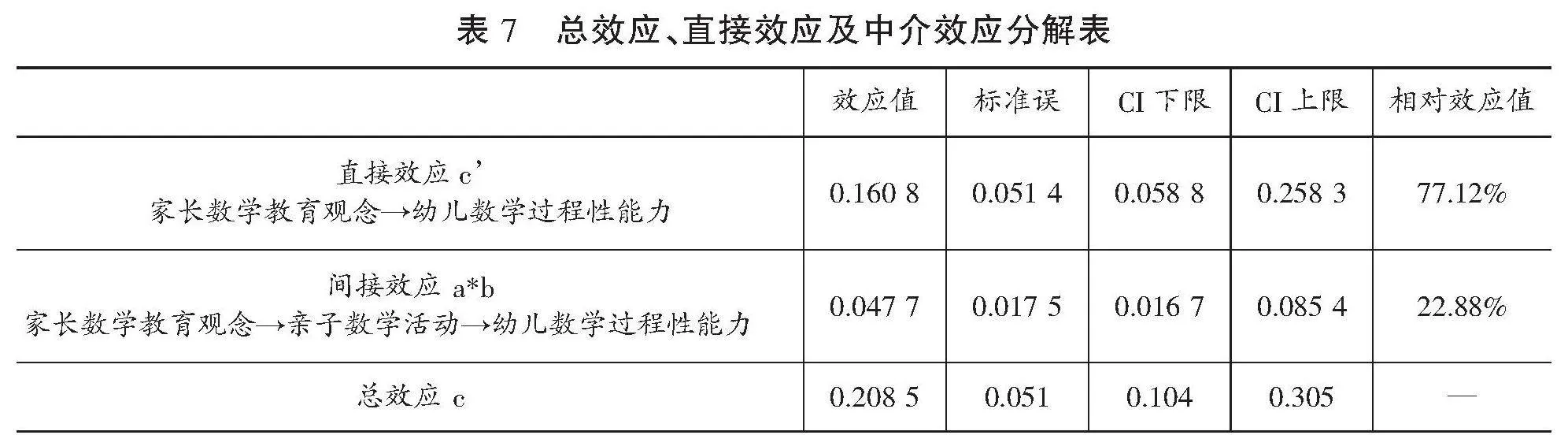
表7 总效应、直接效应及中介效应分解表

■

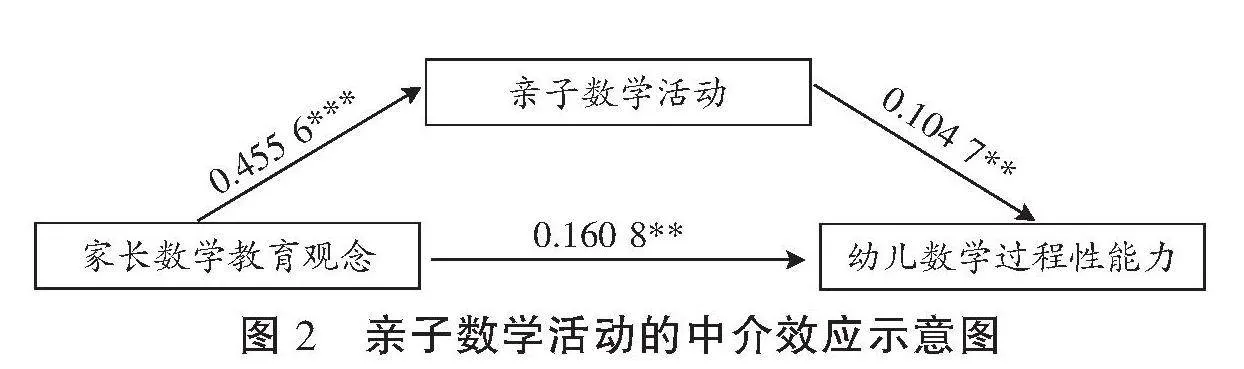
结果显示，亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间的中介效应95%置信区间为[0.016 7，0.085 4]，不包括0，说明亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间的中介效应显著，中介效应大小为0.047 7。此外，在控制中介变量亲子数学活动后，自变量家长数学教育观念对因变量幼儿数学过程性能力的95%置信区间为[0.058 8，0.258 3]，不包括0，说明家长数学教育观念对幼儿数学过程性能力的影响显著。因此，亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间起到部分中介作用，直接效应占比77.12%，间接效应占比22.88%。据此构建出家长数学教育观念影响幼儿数学过程性能力的中介效应图。（见图2）

■

图2 亲子数学活动的中介效应示意图

（五）亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间的具体中介效应

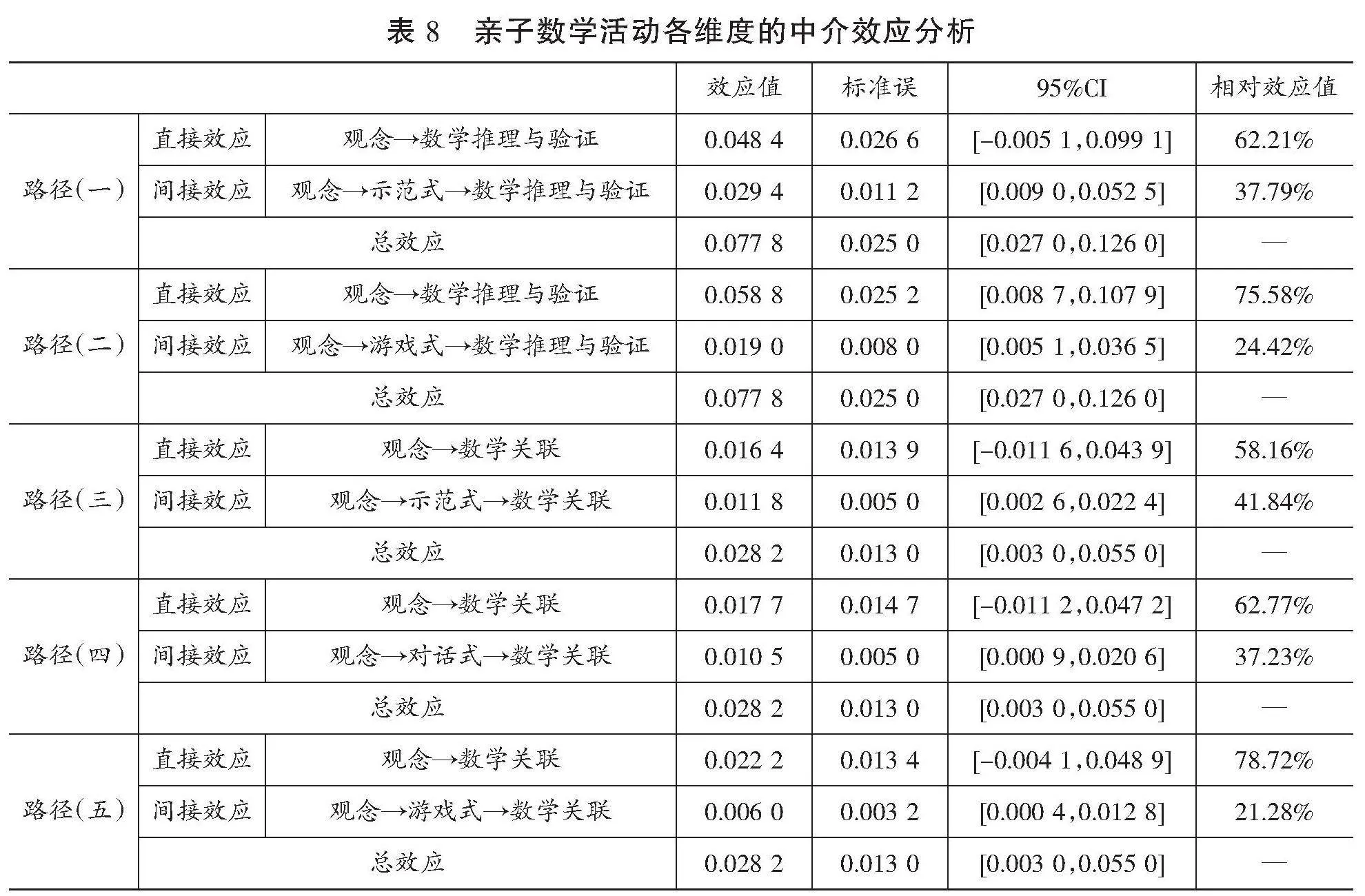
前文研究结果表明，亲子数学活动各个维度与家长数学教育观念以及幼儿数学过程性能力中的数学推理与验证能力、数学关联能力存在显著相关，且家长数学教育观念可以显著正向预测幼儿的数学推理与验证能力和数学关联能力。同时通过线性回归检验可知，示范式教导（t=3.519，p＜0.001；t=2.933，p＜0.01）、对话式教导（t=2.823，p＜0.01；t=2.695，p＜0.01）、直接式教导（t=2.587，p＜0.05；t=2.077，p＜0.05）和游戏式教导（t=3.325，p＜0.01；t=2.317，p＜0.05）可以分别显著正向预测幼儿的数学推理与验证能力以及数学关联能力。因此，可以探究亲子数学活动各个维度在家长数学教育观念及幼儿的数学推理与验证能力、数学关联能力之间的具体中介作用机制。本研究将亲子数学活动的各个维度作为中介变量加入家长数学教育观念对幼儿的数学推理与验证能力和数学关联能力之间构建多重中介模型。（见表8）

表8 亲子数学活动各维度的中介效应分析

■

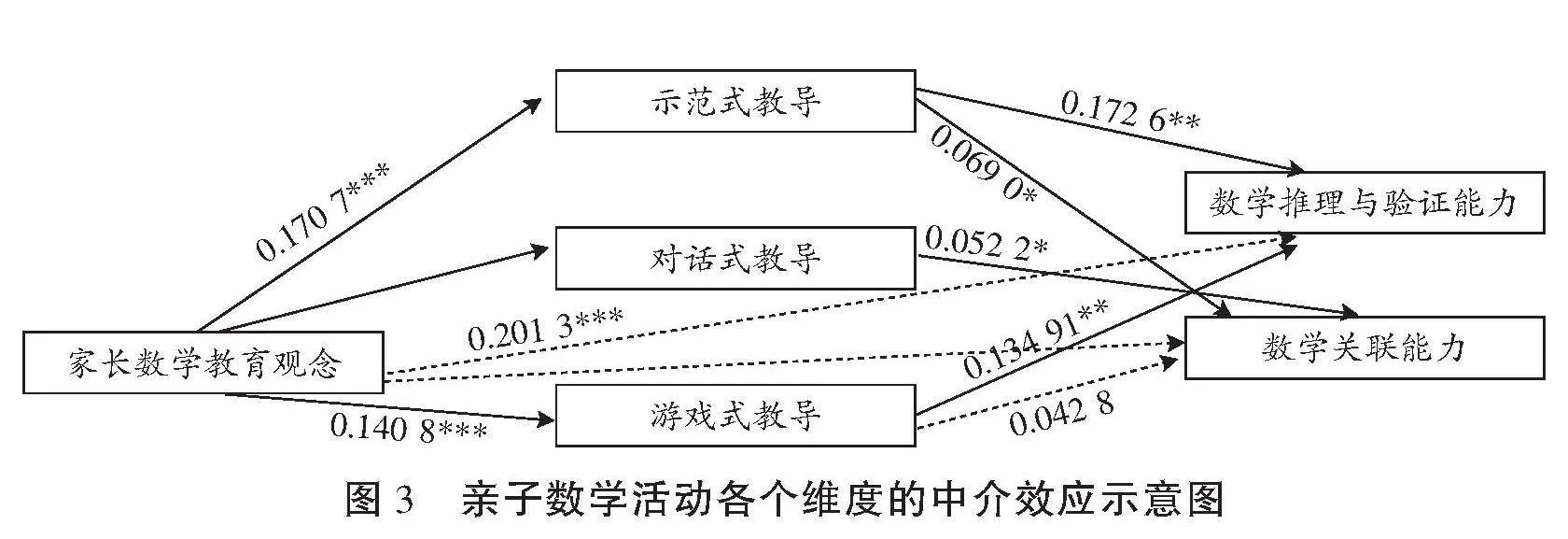
结果显示，示范式教导在家长数学教导观念和幼儿的数学推理与验证能力、数学关联能力之间起完全中介作用；对话式教导在家长数学教导观念和幼儿的数学关联能力之间起完全中介作用；游戏式教导在家长数学教导观念和幼儿的数学推理与验证能力之间起部分中介作用（效应占比为24.42%），在家长数学教导观念和数学关联能力之间起完全中介作用（95%的置信区间均不包含0）；直接式教导的中介效应不显著（95%的置信区间包含0）。这表明在亲子数学活动内部，学前儿童家长的示范式教导、对话式教导和游戏式教导的中介效应值得关注。本研究据此构建出亲子数学活动各个维度在家长数学教育观念和幼儿数学过程性能力之间的中介效应图。（见图3）

■

图3 亲子数学活动各个维度的中介效应示意图

四、讨论

（一）家长的建构式教导观念更能促进幼儿数学过程性能力的发展

本研究结果显示，家长的数学教育观念越趋向于建构型，幼儿的数学过程性能力就发展得越好。其原因可能如下。第一，从数学过程性能力的内在发生机制来看，幼儿数学过程性能力是幼儿在数学学习过程中所获得的理解和运用数学知识的能力，是幼儿数学思维的具体体现，而这种能力的获得往往发生在亲子、师幼之间的数学互动过程中，[35][36]具有过程性、生活性、游戏性等特点。家长在指导幼儿进行数学学习时，会依据自己的目的和意图，采取相应的互动行为，进而影响幼儿的数学学习。如果家长的数学教育观念趋向于建构型，那么其教育往往会以教会幼儿如何学习为主，而非掌握具体的数学知识，进而影响幼儿数学过程性能力的发展。比如，在建构教导历程观维度得分越高的家长越认同应该为幼儿提供问题解决及探索的机会的理念，鼓励幼儿思考，此时家长主要承担引导者和促进者的角色。在建构知识学习观维度得分越高的家长，越认同幼儿的数学学习主要靠幼儿操作、探索来建构知识的理念，强调幼儿对数学的理解和应用。由此可见，持建构型数学教育观念的家长会更注重儿童的数学问题解决、探索建构和理解应用，这正好能够促进数学过程性能力中数学推理与验证、数学交流、数学关联以及数学表征能力的发展。第二，家长数学教育观念会影响家庭数学环境的设置。有研究表明，家长数学教育观念越趋向于建构主义，就越容易给幼儿提供一些具体的、生活化的、可操作的低结构材料，如快递盒子、冰棍棒、毛线球、泡沫板、积木块、七巧板以及数字棋盘游戏等，这些低结构、多玩法的数学玩教具更易于满足幼儿的不同需求，能够激发其创造力，进而提升幼儿的数学思维能力。

（二）亲子数学活动在家长数学教育观念作用于幼儿数学过程性能力时的中介作用

本研究结果表明，亲子数学活动在家长数学教育观念与幼儿数学过程性能力之间起部分中介作用。这一研究结果与前人研究结果相似。如杨青青等人在研究中指出，家庭简单数学活动在父母对幼儿简单数学技能学习的年龄期望与幼儿简单数感能力的关系中起部分中介作用，而家庭复杂数学活动在父母对幼儿复杂数学技能学习的年龄期望与幼儿复杂数感能力的关系中起完全中介作用。[37]儿童的学习方式是由直接学习和成人带有意图、超越和意义互动的中介学习组成。[38]在中介学习中，家长把自己已有的意图和理念实施到亲子互动过程中，并根据幼儿现有发展水平调整与其互动的方式和内容，进而促进幼儿数学思维的发展。[39]国外学者Sigel总结了家长教育观念影响幼儿发展的三种方式，其中一种指出，作为行为发生的心理来源，教育观念以教育行为为中介来促进幼儿的发展，而这一中介作用必须通过亲子互动来完成。[40]本研究结合前文数据，进一步讨论亲子数学活动在家长数学教育观念对幼儿数学推理与验证能力以及数学关联能力发展影响的具体中介作用过程。

其一，亲子数学活动在家长数学教育观念作用于幼儿数学推理与验证能力发展中的中介作用。幼儿的数学推理与验证能力是指幼儿通过对数学对象进行逻辑思考，提出数学设想，并通过给出证明或举出反例来说明自己的数学设想是否合理的能力。[41]数学推理就是从相似的或已知的问题推出新问题的过程。在推理过程中，儿童不仅需要正确操作关系映射，还要反思先前的知识，这个过程就是元认知监控的过程。[42]因此，幼儿在问题解决的过程中对认知过程的监督、调整、反思和评价能够促进幼儿数学推理与验证能力的发展。在示范式教导中，家长主要采取举例说明或利用实物等方式支持幼儿的数学学习。在这一过程中，家长会向幼儿展示某些数学问题的解决策略（如利用实物进行加减运算）。有研究表明，策略使用与幼儿的元认知调节有关，[43]如果幼儿能够采用较好的策略，其元认知调节也会得到更好的发展，进而促进幼儿推理验证能力的发展。在游戏式教导中，幼儿的数学行为往往是自发的，具有积极、自主等特点，[44]他们会更加自主和放松地提出自己的数学设想，按照自己的设想去解决问题，并在尝试中验证自己的设想。幼儿的元认知体验主要是在游戏活动中发生的，[45]他们通过游戏获得对各种事物的认识，进而丰富自己的元认知体验。游戏式教导为幼儿提供了重复练习的机会，让幼儿按照自己的方式去建构、探索和验证自己的设想，进而寻找合适的策略来解决问题。[46]因此，示范式教导和游戏式教导可以通过发展幼儿的元认知能力来影响其数学推理与验证能力的发展。

其二，亲子数学活动在家长数学教育观念作用于幼儿数学关联能力发展中的中介作用。幼儿的数学关联能力是指幼儿在数学知识、数学观点之间建立联系，并能够用数学知识去解决数学以及非数学情境中的问题的能力。[47]在示范式教导中，家长会向幼儿示范如何将新知识与已有知识进行联系，以及如何运用不同的数学方法去解决数学问题，[48]幼儿则会把家长示范的这些信息同化到他们已有的知识结构中去并对这些信息做出解释和重构，进而生成新的认知结构。幼儿在同化和顺应过程中所表现出的整合以及应用能力能够在一定程度上促进其数学关联能力的发展。此外，幼儿的迁移和概括能力也会促进其数学关联能力的发展。[49]在示范式教导中，家长通过提供与幼儿原有知识经验相似的示范内容，能够在一定程度上促进幼儿数学迁移能力的发展。家长向幼儿示范表征某一数学学习对象的具体实物模型或物理情境的各种变式，不仅可以满足不同幼儿的认知风格，还能帮助他们从多种具体模型中抽象出数学结构，进而促使幼儿把从当前情境中获得的数学知识迁移和运用到其他学习情境中去。[50]此外，幼儿的多元表征能力也能促进其数学关联能力的发展，多元表征在不同程度上可以为幼儿提供有关学习对象内部的更多信息，从而使幼儿将一种较为熟悉的表征形式的理解迁移到另一种表征形式上去。在对话式教导中，家长可以在与幼儿对话的过程中进行不同表征形式的变换，通过语言与非语言表征的置换或是将语言表征与现实情境相联系来促进幼儿数学关联能力的发展。例如，“带孩子一起买东西的时候，家长和他/她讨论商品的价格”这一方式便能够在口头数词和数学符号表征方面进行关联，且与幼儿的现实生活相关。[51]

另外，幼儿可以通过玩数学游戏来学习数学知识和发现数学结构，这些游戏的对象就是数学学习对象的多元具体化表征。[52]在游戏式教导中，家长所采用的数学游戏，如情境性游戏、操作性游戏、感官游戏、口头游戏以及竞赛性游戏等都蕴含了多元表征。这种将幼儿所学到的数学概念在游戏中进行表征和表现的方式，能够锻炼幼儿的迁移和转换能力，促进幼儿数学关联能力的发展。

五、教育建议

（一）帮助家长树立建构型数学教育观念

当前家长数学教育观念、亲子数学活动以及幼儿数学过程性能力均处于中等水平，仍然存在家长数学教育意识淡薄、家长对幼儿数学过程性能力的理解存在偏差等问题，因此需要进一步帮助他们树立建构型数学教育观念。波斯纳提出的概念转变模型认为，当学习者学习一个新概念时，若能满足四个条件（不满足、可理解性、合理性、有效性），学习者自然而然就愿意接受新概念。[53]具体到家长建构型数学教育观念的转变，就可以解释为：首先要让家长对自己原有的数学教育观念（传统型数学教育观念）产生不满，然后将一个通俗易懂、听起来合理的、可理解的、新的数学教育观念（建构型数学教育观念）呈现给家长，最后让家长看到建构型数学教育观念对幼儿的数学学习是有促进作用的。

在幼儿园层面，一是要帮助家长了解传统型数学教育观念的弊端。幼儿园可以提供一些传统型数学教育活动视频，让家长观察在传统型数学活动中幼儿注意力不集中、学习兴趣低下、数学能力得不到提升等情况，进而反思传统数学教育观念；通过模拟情景课堂，让家长扮演孩子，分别让其体验和感知教授型和探究型数学活动带给自己的不同感受，进而将其迁移到孩子身上。二是让家长认同并接受建构型数学教育观念。幼儿园可以通过拍摄高质量的幼儿数学活动录像，让家长通过生动的画面，看到孩子在游戏、生活、操作中所体现出来的数学问题解决能力，或者通过设置“我和孩子共同活动”“家庭数学教育活动优秀案例分享”等活动让家长感知建构型数学教育观念带给幼儿数学学习的有效性，[54]以此来强化家长对建构型数学教育观念的认识。三是开展家庭数学教育指导项目，让家长在真实的数学亲子互动中践行建构型数学教育观念。大量实证研究表明，此类项目通常能够取得良好效果。以“带回家的数学包”干预项目为例，家长每周从幼儿园领取一些数学操作材料，回家与孩子一起操作，干预者给家长提供一些与孩子互动时的指导语言和回应策略。5周后，家长对数学的态度明显更加积极。[55]

在社区层面，社区在推动父母教育理念变革方面扮演着举足轻重的角色。社区通过组织集体行动和构建对话与合作平台，能够有效促进家长间的深入交流，进而拓展其对教育实践的理解与认知，为家长教育观念的改变提供了可能性。[56]但鉴于家长分散在社区各处，不易组织面对面的活动，社区可以考虑利用网络资源，积极探索构建家长教育信息交流平台。借鉴前人的研究结果，[57]在线平台可以涵盖专家讲座、数学启蒙案例分享、亲子活动推荐、数学教育问答等模块，定期邀请儿童数学教育领域的专家开展专题讲座，分享成功的数学启蒙实践案例，为不同年龄段的幼儿提供详细的数学亲子活动指南及所需材料清单，鼓励家长提出关于数学启蒙的问题，形成互动的学习氛围。

（二）提高家长的亲子数学活动水平

2018年，美国教育部通信与外联办公室（OCO）发布的《家长的力量：搭建通往成功的桥梁》报告指出，家长参与是学校教育成功的重要因素，在缩小不同学生群体成绩差距方面尤为显著。[58]但从本文的调查数据来看，“每天与孩子开展亲子数学活动”的家长仅占2.2%，那些“生活中开展亲子数学活动”的题目，家长汇报的频率也都不高。为此，一方面，家长应敏锐地捕捉生活中的数学教育机会，为幼儿提供实用资源和个性化指导。在日常生活中，家长可以巧妙地融入数学元素。例如，在超市购物时，家长可以与幼儿一起讨论10块钱可以买哪些东西，鼓励孩子表达自己的思考过程，如“你是怎么想的？”“为什么要这么做呢？”以及“你还有其他方法吗？”等等，让幼儿通过这些活动在日常生活中自然地接触和理解数学概念，锻炼数学思维，在生活实践中发展幼儿的数学过程性能力。[59]

另一方面，社区、图书馆等公共机构也可以为亲子数学活动的开展提供支持。例如，在加拿大，有200多个玩具图书馆向家长开放，旨在教父母如何游戏和使用玩具，帮助家长获得与其他家长、教师交流的机会以及育儿、玩具选择等方面的知识。[60]韩国的绿色玩具图书馆也围绕玩具开展了各类主题活动（如操作性游戏、拼图等），为幼儿及家长提供服务和互动指导。[61]我国各种形式的玩具图书馆约有1 700家，[62]以儿童和家庭为服务对象的“公益+低偿”社区玩具图书馆在北京、上海、杭州等地均有设立，这些都为亲子互动和家庭教育提供了支持。[63]在未来，政府及有关部门可以采取更广泛的政策措施，加大有关场馆的建设，为更广泛地区的幼儿及其家庭提供教育支持。

（三）采取不同的亲子数学活动方式提升幼儿的数学过程性能力

幼儿的元认知能力是影响其数学推理与验证能力的重要因素，幼儿对新旧知识的联结能力、迁移能力以及多元表征能力与其数学关联能力密切相关。而亲子互动中家长的支持策略又能够影响幼儿的元认知等能力，进而影响其数学能力的发展。[64]因此，家长可以利用亲子数学活动中的示范式教导、对话式教导、游戏式教导来促进幼儿数学推理与验证能力以及数学关联能力的发展。

首先，在示范式教导中，家长可以在给幼儿讲解数学问题时，把自己做题的思路示范给幼儿，向幼儿阐述自己在问题解决过程中监控、反思和调节的过程。在示范过程中，家长要观察幼儿对实际问题的掌握情况，并结合数学知识的难易程度来调整示范程度，较难理解的数学知识采取小步子原则并提供具体的指导，较易理解的数学知识则给予幼儿更多自主探索的机会，[65]以此来锻炼幼儿的数学推理与验证能力。家长还可以采取这一教导方式来促进幼儿数学关联能力的发展。比如，一家人准备乘坐火车旅游，幼儿不知道自己是否需要买票，家长可以向幼儿示范测量身高的方法和过程。在这个过程中，幼儿就能够把测量的相关知识（起点与终点、尺子拉平等）、数符号和自己的生活情境关联起来，进而锻炼数学关联能力。再如，家长可以为幼儿提供多元化的操作材料（包括具体的真实物体、相关的教具模型等不同类型的材料），让幼儿在操作中理解数学知识。家长在示范的过程中可采取不同的表征形式来呈现数学知识，如家长示范数数时，可以数3个橘子、3颗糖，也可以数3个点子或者3条竖线，以此促进幼儿数学关联能力的发展。[66]

其次，在对话式教导中，家长可以通过刺激幼儿多元表征能力的发展来促进其数学关联能力的发展。值得注意的是，对话的内容和层次不同，其所达到的教育效果也不同。因此，家长在与幼儿对话时要注意对话的深度、宽度和层次，对话的内容要具有一定的启发性，蕴含一定的数学思维。在与幼儿对话的过程中，家长可以选取与幼儿生活经验相联系的问题，将抽象的数学概念用幼儿熟悉的内容表征出来，以此来锻炼幼儿的数学关联能力。[67]如在送幼儿去幼儿园的路上，引导幼儿观察并说出斑马线或者红绿灯的排列规律；在与幼儿玩低结构数学玩具时，让幼儿说一说“你是怎么想的？”“为什么要这么做呢？”“你还有其他办法吗？”等等。

最后，在游戏式教导中，家长可以利用“元认知游戏循环圈”促进幼儿数学推理与验证能力的发展。在游戏活动前，家长可以与幼儿讨论任务和策略问题，引导幼儿对数学活动进行计划和设想；在游戏活动中，为幼儿提供丰富的游戏材料和时间，家长充当幼儿学习的“脚手架”，丰富幼儿的元认知体验；在游戏活动后，引导幼儿对自身的认知过程进行反思，以此来促进幼儿数学推理与验证能力的发展。[68]以“套圈”这一竞赛性游戏为例，游戏前家长要和幼儿一起讨论每人几个圈、站在哪里扔圈等游戏规则，并启发幼儿思考如何才能套中更多，如何才能记清每个人的套圈清楚成绩，等等。游戏中，家长要提供充足的套圈材料并全身心投入游戏，不要过多干预幼儿，当幼儿出现诸如不清楚如何记录每人每轮的套圈成绩等问题时，家长可以及时与他们讨论并提供适当的帮助。游戏后，家长应与幼儿一同回顾游戏过程，分析赢家胜出的原因，探讨在记录成绩过程中遇到的困难及其解决方案。在数学关联能力发展方面，家长可以利用游戏活动中道具、形象及操作等多种表征的作用，提高幼儿的数学关联能力。[69]比如，家长可以和幼儿玩“算数扑克牌”的游戏，每次选择两张扑克牌，家长和幼儿通过比赛的形式将扑克牌上的数字换算成数学等式，看看谁的办法多，算得又正确，通过对多种表征形式的迁移和转换来帮助幼儿感知、理解和掌握数概念。

（四）重视动机、兴趣、态度、情感等非智力因素对幼儿数学过程性能力发展的影响

幼儿数学过程性能力的发展不仅会受到认知能力的影响，还会受到动机、兴趣、态度、情感等非智力因素的影响，而成功的数学学习者往往具有积极的数学学习态度、兴趣、情绪、情感和自信心。[70]具有高度自信的幼儿不会怕自己出错、出糗，他们在数学学习中会积极地开展数学问题解决活动、表达自己的数学观点、大胆地提出自己的数学设想并敢于尝试去验证，这些积极的非智力因素会在一定程度上促进幼儿的数学思维、数学问题解决以及数学过程性能力的发展。[71]因此，家长在进行亲子数学活动时要注重对幼儿进行鼓励，避免向幼儿传递出数学是枯燥或难以掌握的观点。美国教育心理学家卡罗尔·德韦克的研究就指出，如果家长鼓励孩子将努力而非天赋视为成功的关键，那么孩子就会对学习数学表现出积极的态度，从而在面对数学难题时更坚韧、更有自信。[72]因此，家长在利用对话式教导时要给予幼儿解决问题的信心，尽量减少自身消极情绪的输出，多鼓励、多表扬幼儿；在利用示范式教导时，要时刻关注幼儿的态度和兴趣，尽量给幼儿提供直观、形象、可操作的玩教具，根据幼儿的发展水平因材施教；在利用游戏式教导时注重幼儿自主性的发挥，选择幼儿感兴趣的数学游戏，同时注意游戏的深度和难度，防止游戏互动流于表面。

（本研究得到了温州大学附属实验幼儿园陈娴园长、温州市龙湾罗西幼儿园邵云连园长、温州市瓯海梧田欣园幼儿园林盈盈副园长、温州市乐清教育局叶旭丹老师的大力支持，在此一并表示感谢！）

参考文献：

[1]MACK N K. Engaging young children in mathematics： standards for early childhood mathematics education[J]. Teaching Children Mathematics，2004，11（1）：46-47.

[2][34]周晶，郭力平.5～7岁儿童数学过程性能力构成要素探索与模型建构[J].学前教育研究，2018（02）：12-24.

[3]SERAFINO K， CICCHELLI T. Cognitive theories， prior knowledge， and anchored instruction on mathematical problem solving and transfer[J]. Education and Urban Society，2003，36（1）：79-93.

[4]NUNES T， BRYANT P， EVANS D， et al. The contribution of logical reasoning to the learning of mathematics in primary school[J]. British Journal of Developmental Psychology，2007，25（1）：147-166.

[5]CHUNG N， RO G. The effect of problem？鄄solving instruction on children’s creativity and self？鄄efficacy in the teaching of the practical arts subject[J]. Journal of Technology Studies， 2004，30（2）：116-122.

[6]NUNES T， BRYANT P， BARROS R， et al. The relative importance of two different mathematical abilities to mathematical achievement[J]. British Journal of Educational Psychology，2012，82（1）：136-156.

[7]MANOLITSIS G， GEORGIOU G K， TZIRAKI N. Examining the effects of home literacy and numeracy environment on early reading and math acquisition[J]. Early Childhood Research Quarterly，2013，28（4）：692-703.

[8]DEL R？魱O M F， SUSPERREGUY M I， STRASSER K， et al. Early sources of children’s math achievement in chile： the role of parental beliefs and feelings about math[J]. Early Education and Development， 2021，32（5）：637-652.

[9]LEECH K A， HERBERT K， YANG Q T， et al. Exploring opportunities for math learning within parent？鄄infant interactions[J]. Infant and Child Development，2022，31（2）：e2271-e2286.

[10][18]张华，庞丽娟，许晓晖，等.家庭生态环境与儿童早期数学认知能力[J].北京师范大学学报（社会科学版），2005（03）：55-61.

[11]程祁.家庭文化资本及其对幼儿数学学习的影响研究[D].上海：华东师范大学，2009：97-98.

[12]LEVINE S C， SURIYAKHAM L W， ROWE M L， et al. What counts in the development of young children’s number knowledge？[J]. Developmental Psychology，2010，46（5）：1309.

[13]PEZDEK K， BERRY T， RENNO P A. Children’s mathematics achievement： the role of parents’ perceptions and their involvement in homework[J]. Journal of Educational Psychology，2002，94（4）：771.

[14]王曲.母亲教养方式与幼儿数学水平发展[D].芜湖：安徽师范大学，2010：31-33.

[15][28][32]黄瑾，程祁.家庭文化资本对幼儿数学学习的影响[J].心理科学，2011，34（6）：1385-1389.

[16]胡丽园.父母数学教育观念及其与儿童数概念发展关系的研究[D].广州：华南师范大学，2007：46-47.

[17]SKWARCHUK S L， SOWINSKI C， LEFEVRE J A. Formal and informal home learning activities in relation to children’s early numeracy and literacy skills： the development of a home numeracy model[J]. Journal of Experimental Child Psychology，2014，121（1）：63-84.

[19]LEFEVRE J A， POLYZOI E， SKWARCHUK S L， et al. Do home numeracy and literacy practices of Greek and Canadian parents predict the numeracy skills of kindergarten children？[J]. International Journal of Early Years Education，2010，18（1）：55-70.

[20]王洛丹.母亲的教养方式与儿童数概念的发展[D].上海：华东师范大学，2005：66-67.

[21]黄瑾.家庭与幼儿早期数学认知能力发展[J].幼儿教育（教育科版），2006（11）：45-48.

[22]ZHOU X， HUANG J， WANG Z， et al. Parent？鄄child interaction and children’s number learning[J]. Early Child Development and Care，2006，176（7）：763-775.

[23]周欣，黄瑾，王正可，等.父母—幼儿共同活动中的互动与幼儿的数学学习[J].心理科学，2007，30（3）：579-583.

[24]周欣，赵振国，毛尼娜，等.日常家庭生活中父母—儿童互动对儿童数学发展的影响[J].学前教育研究，2007（7-8）：116-121.

[25]刘育明.弗斯坦中介学习经验理论及其工具强化[J].外国教育资料，1988（01）：45-48+29.

[26]张瑞峰.回应式养育理论下亲子游戏互动质量研究[D].大连：辽宁师范大学，2021：57-58.

[27]师保国，申继亮.家庭社会经济地位、智力和内部动机与创造性的关系[J].心理发展与教育，2007（01）：30-34.

[29]GAY L R， MILLS G E， AIRASIAN P W. Educational research： competencies for analysis and applications[M]. Boston： Pearson，2012：165-167.

[30]NUNNALLY J C. Psychometric theory[M]. 2nd ed. New York： McGraw？鄄hill，1978：269-270.

[31]吴明隆.SPSS统计分析实务：SPSS操作与应用[M].重庆：重庆大学出版社，2010：243-244.

[33][44]刘焱.儿童游戏通论[M].福州：福建人民出版社，2015：193，226.

[35]费广洪，赵嘉茹，汪文娟.成人提问的认知水平与模式对5岁儿童问题解决的影响[J].学前教育研究，2012（11）：20-25.

[36]SHIAKALLI M A. Constructing squares as a mathematical problem solving process in pre？鄄school[J]. Review of Science， Mathematics and ICT Education，2014，8（1）：43-61.

[37]杨青青，潘月娟，朱媛媛，等.父母对幼儿数学学习的年龄期望与幼儿数感能力的关系：家庭数学活动的中介作用[J].幼儿教育，2019（18）：32-37+54.

[38]丁邦平.中介学习经验理论与幼儿智力发展[J].学前教育研究，1995（05）：6-8.

[39]邹晓燕，陈巍.维果茨基社会文化发展理论及其对幼儿园社会教育的启示[J].学前教育研究，2007（06）：27-30.

[40]SIGEL I E. The relationship between parental distancing strategies and the child’s cognitive behavior[C].//Families as learning environments for children. Boston， MA： Springer US，1982：47-86.

[41][47]周晶.5～7岁儿童数学过程性能力的构成要素及应用性研究[D].上海：华东师范大学，2016：61，62.

[42]孙崇勇.儿童元认知发展对推理能力的影响[J].陕西学前师范学院学报，2016，32（1）：69-74.

[43]张亚杰.5～6岁儿童数学活动中的元认知发展和干预研究[D].上海：华东师范大学，2014：36.

[45]江玲，朱琦，王红，等.本体性游戏与幼儿元认知发展的研究[J].集美大学学报（教育科学版），2003（01）：47-55.

[46]张亚杰.5～6岁儿童数学元认知知识的发展研究[J].早期教育（教科研版），2017（10）：11-15.

[48]赵南.“最近发展区”概念解析及其对幼儿园教学的启示[J].学前教育研究，2006（09）：5-9.

[49][70]曹才翰，蔡金法.数学教育学概论[M].南京：江苏教育出版社，1989：97-106，120.

[50]黄瑾，徐雅萍.多元表征与早期儿童的数学学习[J].幼儿教育，2013（1-2）：14-15.

[51]严秀英.多元表征学习模型对幼儿双语教学的启示[J].黑龙江教育学院学报，2013，32（9）：90-91.

[52]黄瑾.论学前儿童数学学习中的多元表征[J].全球教育展望，2011，40（1）：60-63.

[53]李娟.促进教师观察了解儿童学习与发展水平的研究[D].上海：华东师范大学，2011：65.

[54]何黎明.家园互动：提升家长的家庭教育观念和教育能力[J].早期教育（增刊），2004（09）：17-19.

[55]LINDER S M， EMERSON A. Increasing family mathematics play interactions through a take？鄄home math bag intervention[J]. Journal of Research in Childhood Education，2019，33（3）：323-344.

[56]WILLIS L D. Exploring cogenerativity for developing a coteaching community of practice in a parent？鄄teacher engagement project[J]. International Journal of Educational Research，2016，80（1）：124-133.

[57]SHERIDAN K M， WEN X. Evaluation of an online early mathematics professional development program for early childhood teachers[J]. Early Education and Development，2021，32（1）：98-112.

[58]U.S. Department of Education. Parent power： build the bridge to success[EB/OL].（2018-11-19）[2023-10-03].https：//www2.ed.gov/parents/academic/help/parentpower/booklet.pdf.

[59]LEYVA D， DAVIS A， SKORB L. Math intervention for Latino parents and kindergarteners based on food routines[J]. Journal of Child and Family Studies，2018，27（6）：2541-2551.

[60]王伊莹，蔡迎旗.国外儿童玩具图书馆的运行机制及启示[J].幼儿教育，2022（1-2）：92-95.

[61]陈璐.韩国首尔绿色玩具图书馆的服务及启示[J].图书馆工作与研究，2020（06）：49-54+80.

[62]石晶.我国省级公共图书馆玩具图书馆服务[J].图书馆论坛，2018，38（3）：2-5.

[63]雷万鹏，向蓉.家庭教育指导服务的双重差异与政策启示[J].南京师大学报（社会科学版），2022（06）：14-23.

[64]HUANG Q， SUN J， LAU E Y H， et al. Linking Chinese mothers’ and fathers’ scaffolding with children’s initiative and mathematics performance： a moderated mediation model[J]. Early Childhood Research Quarterly，2022，59（1）：74-83.

[65]SAXE G B， GUBERMAN S R， GEARHART M， et al. Social processes in early number development[J]. Monographs of the Society for Research in Child Development，1987，52（2）：101-162.

[66]章佳颖.4～6岁儿童数学认知中的多元表征研究[D].上海：华东师范大学，2011：62-63.

[67]俞莉.多元表征：数学区域活动中发展幼儿数学能力的支持策略[J].福建基础教育研究，2021（09）：124-126.

[68]陈晨.“元认知游戏循环圈”课程提升5～6岁幼儿元认知的实践研究[D].杭州：杭州师范大学，2023：48-49.

[69]秦慧芳.基于多元表征的幼儿数学游戏设计研究[J].延边教育学院学报，2020，34（6）：80-82.

[71]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009：198-199.

[72]WECK C S. Motivational processes affecting learning[J]. American Psychologist，1986，41（10）：1040.

The Relationship Between Parents’ Conceptions on Mathematics Education and Young Children’s Mathematical Process Ability： the Mediating Role of Parent？鄄child Mathematics Activities

LI Juan， DENG Xuechun， WANG Shuqi， ZHANG Yiting

（School of Education， Wenzhou University， Wenzhou 325000 China）

Abstract： Parents’ conceptions of mathematics education and parent？鄄child mathematical activities have a very important influence on young children’s mathematical process ability. In order to discuss the relationship between parents’ conceptions of mathematics education， parent？鄄child mathematical activities， and young children’s mathematical process ability， this study took 280 pairs of kindergarten children and their parents from three kindergartens in W City， Zhejiang Province as subjects， and used the Parents’ Conceptions of Mathematics Education Scale， Questionnaire of Parent？鄄Child Mathematical Activities， and Checklist of Young Children’s Mathematical Process Ability to investigate the effects of parents’ conceptions of mathematics education and parent？鄄child mathematical activities on young children’s mathematical process ability and to analyze the mediating role of parent？鄄child mathematical activities. The results showed that parents’ conceptions of mathematics education， parent？鄄child mathematical activities and young children’s mathematical process ability were basically in the middle level， and that there was a significant and positive correlation between parents’ conceptions of mathematics education， parent？鄄child mathematical activities and young children’s mathematical process ability. Meanwhile， parents’ conceptions of mathematics education and parent？鄄child mathematical activities positively predicted young children’s mathematical process ability. Parent？鄄child mathematical activities partially mediated the relationship between parents’ conceptions of mathematics education and young children’s mathematical process ability， while the specific dimensions of parent？鄄child mathematical activities， i.e.， demonstrative teaching styles， fully mediated young children’s mathematical reasoning and validation competence and mathematical associative competence. Conversational teaching styles fully mediated young children’s mathematical associative competence； playful teaching styles partially mediated young children’s mathematical reasoning and validation competence， and fully mediated their mathematical associative competence. The mediating effect of direct teaching styles was not significant. The development of young children’s early childhood mathematical process skills can be achieved by establishing parents’ concept of constructive education， improving parents’ level of parent？鄄child activities， adopting different ways of parent？鄄child activities， and emphasizing children’s non？鄄intellectual factors.

Key words： parents’ conceptions on mathematics education； mathematics process skills； parent？鄄child mathematics activities

（责任编辑：黎勇）