实践中明理 探究中寻法

刘群 黄家兴

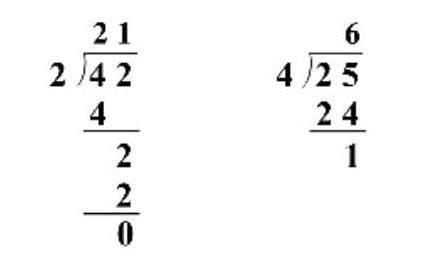
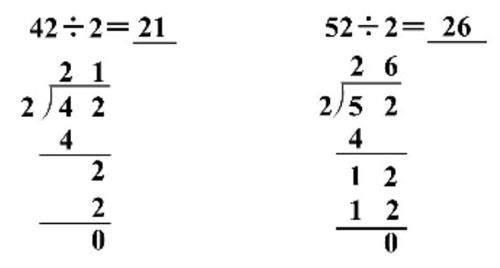
计算教学不仅是提升小学生运算能力的重要方法，还是锻炼他们逻辑思维的重要途径。因为学生只有在深入理解算理的基础上熟练掌握算法，才能真正提升运算能力，所以教师在教学中不能局限于传授计算技巧，而要注重算理与算法的融合。笔者以人教版数学三年级下册“一位数除两位数（商是两位数）的笔算除法”教学为例，阐述如何引导学生在实践探究中明理、寻法。

一、读懂教材和教参，明晰教学目标

教材和教参是教师理解学科知识体系、把握教学重难点的重要工具。教师必须在熟悉课程标准要求的基础上认真研读教材和教参，深入理解其编排意图，确保教学的科学性和有效性。

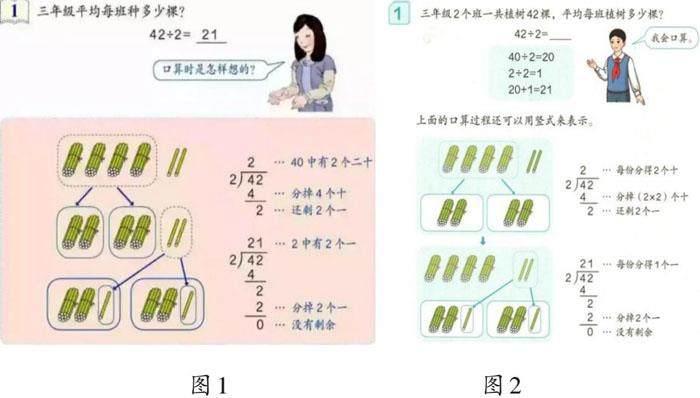
对比新旧两版教材（图1旧版、图2新版）可以发现，新版教材细化了口算过程和小棒图呈现的内容。新版教材的学习提示语由旧版“口算时是怎样想的”改为“我会口算”，意在向学生渗透可以直接借助前面学习口算（一位数除两位数）获得的经验解决问题，即结合口算思路，借助小棒图理解除的过程和竖式写法。新版教材的小棒图分两层呈现，强调两次平均分的过程和结果，先分4个十，每份分得2个十，再分2个一，每份分得1个一，旨在使学生明确每一次计算的含义，突出计数单位。两次分小棒的过程与除法竖式的两层计算过程结合起来的编排方式，借助“分”的操作，呈现“除”的过程，有助于学生理解算理，掌握除的顺序和竖式写法。

人教版数学教材在编排《除数是一位数的除法》这一单元内容时，将“一位数除两位数”分为两个课时（被除数最高位除完没有余数和被除数最高位除完有余数），体例大致相同。这两个课时的教学内容旨在引导学生用竖式计算除法，例2（52÷2）要解决的主要问题是十位上的数除后有余数应该怎么办。基于这样的思考，笔者尝试将例1（42÷2）和例2进行整合教学，让学生从整体上感受相关计算方法的核心原理和关键环节，在理解和掌握相关数学知识技能的同时锻炼思维能力，感悟思想方法。

二、创设问题情境，激发深度思考

教学中，笔者先让学生思考：“口算42÷2时除了几次？先算什么？再算什么？”学生发现“除了两次，先算40÷2=20，再算2÷2=1”。接着，笔者创设问题情境：“你能把42根小棒平均分成2份，表示出刚刚口算除两次的过程吗？”同时，笔者提示：“平均分42根小棒时分了几次？先分的什么？再分的什么？”学生回答：“分了两次，先分4捆小棒，再分2根小棒。”然后，笔者发放学习单，引导学生尝试用竖式记录两次平均分小棒的过程。学生在学习单上独立尝试后，笔者请学生说说自己的竖式计算过程。一名学生回答：“先分4个十，4个十平均分成2份，每份分得2个十，在十位上商2，分后没有剩余。再分2个一，2个一平均分成2份，每份分得1个一，在个位上商1，分后也没有剩余。”将竖式的建构建立在理解除法意义之上的做法，让学生深入理解了除法竖式中每个数的含义，实现了整数除法算法与算理的贯通。

以上教学，教师通过反复提问“分了几次？先分什么？再分什么？”促进学生操作和思考，使学生明白除法竖式记录的是两次平均分的过程，竖式计算与口算、摆小棒具有一致性，笔算除法就是把口算、摆小棒计算的过程用竖式形式写下来，三者本质上都是依次平均分计数单位的个数。

三、多重对比，实现深度探究

首先，例1（42÷2）竖式与二年级下册表内除法（25÷4）竖式对比。

在教学例1即笔算42÷2后，笔者让学生比较42÷2的笔算除法和二年级下册学习的表内除法25÷4的区别。学生能直观感受到现在学的笔算除法竖式更加复杂，要写两层，商是两位数；以前学的只需要写一层，商只有一位数。通过对比，学生发现一次平均分对应一层竖式，两次平均分对应两层竖式。这样教学打破了学生对除法竖式只有一层结构的原有认知，提升了学生对一位数除两位数的笔算除法算理和算法的理解，为后续学习奠定了基础。

其次，例1（42÷2）竖式与例2（52÷2）竖式对比。

通过例1与例2的除法竖式对比，学生不难发现，两者都是一位数除两位数，商都是两位数，但前者被除数最高位除完没有余数，这时就把个位上的数落下来继续除，而后者被除数最高位除完还有余数，就要把余数和下一位上的数合并后再除。从“最高位能整除”迁移到“最高位不能整除”，学生再次整体比较后发现，虽然被除数的最高位不能全部分完产生了余数，但是除法计算过程中细分计数单位个数的算理是不变的，这体现了“最高位能整除”和“最高位不能整除”的除法算法和算理的一致性。

学习两道例题后，学生对笔算除法的掌握仍然停留在表面，他们更多的是在模仿除的程序，而非真正理解除法算理。因此，教师引导学生对比两道例题的异同，目的在于总结和提炼算法，将知识内化，形成两位数除以一位数的笔算除法的计算模型。通过对比，学生不仅深入理解了算理，还进一步掌握了算法。更重要的是，对比教学使学生感知到知识间的内在联系，为构建相对完整的知识结构提供了连接点和支撑点。

四、分层设计习题，满足多元发展需求

巩固练习环节，原本的设计是直接出示96÷3，78÷2，68÷2，51÷3四道竖式笔算除法题，让所有学生独立写出完整的竖式计算过程。经过教学实践，笔者发现，对少数基础较为薄弱的学生而言，直接写出完整的竖式计算过程有难度。为了充分尊重学生的学习起点，笔者改进了练习设计，先让学生完成下图中左边两道竖式练习，按照提示进行计算，以巩固分两步除、每一步除得的商是多少、应写在哪里等知识点。在指导性练习之后，笔者组织学生巩固算法，完成下图中右边两道竖式练习，帮助学生进一步内化算理，熟悉算法。

学生之间的学习差异是客观存在的，教师在设计习题时应充分考虑学生的实际情况，按照难易程度、知识点覆盖面等维度分层设计。这样做既能让基础薄弱的学生在练习中巩固基础，又能让能力较强的学生在挑战中提升水平，从而更好地满足学生的个性化学习需求，促进全体学生共同进步。

（作者单位：武汉经济技术开发区三角湖小学）

责任编辑  孙爱蓉