基于深度学习的高中新教材概念教学实践研究

［摘 要］ 深度学习是一种新的学习方式，是对传统学习的一种可贵突破，其立足学生的学习实际，强调在学习过程中追求应有的深度；深度学习指向的是学生的思维，指向的是学生在学习过程中的思维深度，强调只有处于深度思维中的学生才能有深度学习的体验. 在理解深度学习时，还应当站在学生的角度去思考，只有适合学生思维深度的学习才是真正有效的深度学习. 基于深度学习的概念教学，一是要关注教学设计能否为学生打开深度学习的大门，二是要关注学生在学习过程中能否真正进入深度学习的状态.

［关键词］ 深度学习；新教材；概念教学；实践研究；三角函数

有人说，深度学习是当今教育改革下一种新的学习方式［1］. 对于这一判断，笔者是认同的，深度学习确实是对传统学习的一种可贵突破，其立足学生的学习实际，强调在学习过程中追求应有的深度，直指传统教学的不足. 也就是说，深度学习指向的是学生的思维，指向的是学生在学习过程中的思维深度，强调只有处于深度思维中的学生才能有深度学习的体验. 在核心素养的背景下，这样的认识显然具有较强的生命力. 与此同时，也应当注意到在理解深度学习的时候，还应当站在学生的角度去思考，只有适合学生思维深度的学习才是真正有效的深度学习. 如果教师完全站在自己的角度，或站在考试的角度去看深度学习，极有可能出现传统教学中的问题，即忽视学生的基础而实施教学，这样的教学很难适合学生的需要，自然也就无法达成真正的深度. 如果教师以为学生在学习时感觉到有难度存在，这样的学习就是深度学习的话，那么显然是对深度学习的错误理解，不利于深度学习的有效开展. 本文以人教A版高中数学（2019版）必修第一册教材第五章“三角函数”的教学为例，重点从概念教学的角度来谈谈一些思考与实践.

深度学习对数学概念教学的影响

在《普通高中数学课程标准（2017年版）》颁布之后，教材也做了相应的修改，因此现在所用的高中数学教材可以说是新教材. 在2020年，课程标准又做了修订，进一步明确了相关要求，这对高中数学教学尤其是概念教学带来了深远的影响.

众所周知，概念是教材中的基础内容，相较于公式的运用、问题的解决，概念的讲解看起来很简单，使得部分教师认为只要学生看一眼就能大概明白其意思. 正因为如此，部分教师在开展课堂教学时会忽视概念，不愿意花费大量时间在概念的讲解上，而愿意让学生去多练习几道题. 但概念是基础、是核心，只有学生真正理解了概念，在接下来的学习中才能得心应手［2］.

上述情形在日常教学中确实客观存在，由于高考并不直接考查数学概念，因此在日常教学中，部分教师会将概念教学的时间节省下来用于学生训练习题，从而让学生在熟能生巧的过程中提升自己的解题能力. 尽管从应试的角度来看，这样的措施能够在一定范围内起到一些效果，但是从长久来看，这样的做法并不能培养学生真正的能力，更谈不上核心素养的发展. 近两年来，数学高考的难度不断增加，仅凭简单的记忆和重复训练已经不足以培养学生的能力，这意味着传统cfb61dade55e9c949de7cbf6ab05751b的重复训练思路已经不适合核心素养以及新高考背景下的教学需求了. 当前的高中数学教学，应当从最基本的概念教学入手，引导学生进入深度学习的状态，让学生在深度学习的过程中建构数学知识，培养数学知识运用能力，从而发展自身的深度思维，培育数学学科核心素养.

在这样的视角下来看深度学习对高中数学概念教学的影响，笔者认为至少应当关注两点：

一是关注教学设计能否为学生打开深度学习的大门.

教师的教学设计对学生学习的影响巨大，教师有怎样的教学设计，基本上就决定学生有怎样的学习过程. 因此，学生能否真正进入深度学习的状态，关键就取决于教师的教学设计. 这意味着教师要想设计具有深度学习特征的教学，首先自己必须清楚深度学习的基本内涵. 有研究表明，深度学习最基本的特征就是让学生从简单的记忆走向深度的理解，也就是摆脱死记硬背的学习，走向理解性学习. 从深度学习的角度来看，学生在理解概念的过程中，必须明白概念之间的关系，带着批判的意识主动建构新概念.

二是关注学生在学习过程中能否真正进入深度学习的状态.

习惯被动接受知识的学生，想要有效切入深度学习，并不是一件容易的事情. 教师的教学设计再好，如果学生不能进入深度学习的状态，也会前功尽弃. 不仅如此，如果教师过于急切地将学生引入深度学习，一样会出现欲速不达的状态，这被多次教学实践证实了. 在教学中，教师并不能完全放弃浅层学习，而应当将必要的浅层学习作为深度学习的基础，让学生在这一基础上能够自主进入深度学习的状态. 这样不仅可以让学生思维的切换更加自如，而且可以激活学生学习的主动性，当学生在这一主动性的作用下进入深度学习并成功建构相关概念时，学生会有更强的收获感，而这又会进一步激活学生的概念学习乃至于整个数学学习的动机，于是深度学习也就能进入良性循环的境界.

基于深度学习的“三角函数”概念教学

从上述分析来看，基于深度学习的概念教学，既适合学生的学习需要，也呼应数学学科核心素养的发展. 在教学实践中，本着学生理解概念与发展核心素养的目的，可以问题驱动核心任务研究，有组织地探索一系列相关问题，帮助学生自主搭建知识结构框架，发展学生的思维链，建立系统的单元知识体系，进而彰显单元知识的整体性和系统性，促进学科核心素养的落地生根［3］.

“三角函数”是高中数学知识体系中的重要知识，学生对三角函数概念的理解程度，不仅影响着三角函数这一知识的学习，还影响着后续与之相关知识的学习. 那么，如何深度学习三角函数这一概念呢？笔者在教学中做了这样的尝试：

首先，创设情境，激活学生已有的经验.

情境对于学生建构数学概念来说，意义不言而喻. 如果能用情境将学生已有的函数学习经验激活，那么学生学习三角函数的概念就有了一个坚实的基础. 在创设情境时，笔者先让学生去思考二次函数的解析式以及图象的变化关系，然后引导学生将思维从角度制转换至弧度制——这一转换比较关键，因为不少学生此时还没有习惯用弧度制来研究问题. 笔者在这里跟学生强调：将角度改成弧度，本质上是将研究的对象从角度转换为实数. 事实证明，通过这样的强调，不仅能激活学生已有的经验，还能让学生期待学习. 弧度制下的函数学习，会有怎样的新内容呢？当学生有了这一问题时，就可以将教学切入下一个环节.

其次，利用直角坐标系，帮助学生建立三角函数的模型.

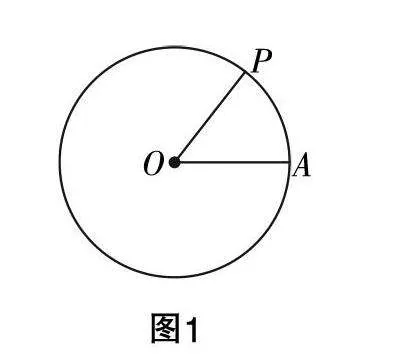
概念的学习本质上就是模型的建构，三角函数模型的建构，关键是在单位圆上进行研究. 借鉴教材进行设计，此处给学生提出的问题是：在单位圆☉O上有一点P，以A为起点做逆时针方向旋转（如图1所示），这可以建立一个怎样的数学模型？描述点P位置的变化情况.

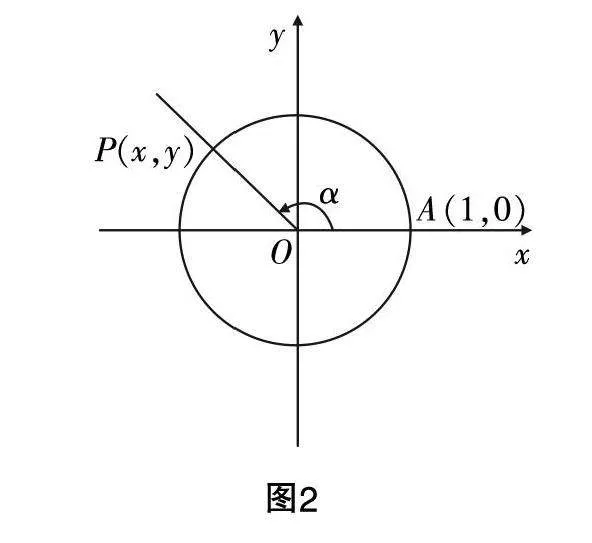
学生面对这一问题时，起初找不到解题方向，这时笔者加以提醒，让学生去建立直角坐标系. 有了这一提醒后，学生就在原有的经验基础上想到将单位圆的圆心作为坐标系的原点，以OA连线作为坐标系的x轴，与之垂直的线作为y轴，于是就建立起了平面直角坐标系，而且点A的坐标是（1，0）（如图2所示）.

当学生能够自主作出这样的图象时，就意味着学生进入了深度学习的状态（此前的经验激活与动机激发过程，可以看作一个浅层学习的过程）. 学生在这样的过程中能够充分建构关于三角函数的认识，如知道P点的运动具有周期性，P点的位置变化可以看作射线OA从非负半轴开始，绕点O按逆时针方向旋转的过程. 此过程中如果借助旋转的角度α，那么就可以描述点P的位置变化. 很显然，当学生认识到这一点的时候，三角函数概念的模型也就被基本建立出来了.

当然，要想丰满模型，还必须进行下一步的探究，比如给α具体数值，然后去探究P点的坐标，并且在此过程中思考：当P点处于同一位置时，α的值是不是唯一的……类似于这样问题的探究，可以让学生进一步认识该模型的作用，从而在强化该模型认同的同时，对三角函数的概念也有了深入的理解.

再次，运用数学语言，帮助学生建构三角函数的概念.

一个数学概念是需要通过数学语言来描述的，此时所用的数学语言可以表现为数学概念的定义，也可以表现为描述数学概念的其他形式，如表格、图象等. 广义的数学模型认识中，在描述高中数学概念时，通常都允许多种形式的存在，三角函数当然也不例外. 教材对三角函数概念的概述，所用的“一般地，任意给定一个角……”就是用文字语言表达与三角函数相关的数学意义，其后所给出的正弦函数、余弦函数，就是对三角函数的进一步丰富. 事实证明，当学生掌握了这些数学语言之后，他们对三角函数概念的理解会更加完整.

对数学概念教学中的深度学习的思考

在上述教学案例中，学生的自主建构过程是非常充分的，学生在这一学习的过程中充分利用自己的经验去建构新概念，通过自主学习与讨论交流，充分利用自己已有的知识去理解三角函数，一旦理解出现了困难，或者当自己的思考与他人不一致的时候，也不会简单地盲从他人，而是在坚持自己思考的基础上去判断他人的观点. 这些学习特征已经充分满足了深度学习的特征，这样的学习过程才是深度学习的过程.

大量的事实表明，通过深度教学，可以促使学生深刻理解概念的内涵和外延，牢固掌握概念，灵活运用概念，指引学生从“浅层学习”走向“深度学习”［4］. 从“三角函数”教学角度来探究深度学习原则，笔者以为在教学中应当坚持这样的起点：一是深度学习的设计与实施要围绕学生展开，这个过程中学生的最近发展区依然需要得到尊重，让学生“跳一跳，摘得到”，才是从浅层学习走向深度学习的合理步骤；二是深度学习要围绕学生的思维展开，学习中的深度本质上是思维的深度，概念教学中的思维深度，体现在学生建构数学概念的时候，能够激活自身的经验，能够与其他概念产生关系，能够形成一个相对完整的模型，当然也能够在具体的情境中加以运用；三是深度学习实施后要进行相应的评价，这是一个容易被忽视的环节，如果教师能够放弃想当然的思路，真正从学生的角度去判断学生的学习过程，那就可以对深度学习有更加准确的把握.

参考文献：

［1］ 姜春冬. 基于深度学习理念下高中数学教学研究——以“对数函数的概念”为例［J］. 数理天地（高中版），2022（12）：39-41.

［2］ 宋艳丽. 基于深度学习的高中数学概念教学［J］. 数理化解题研究，2022（21）：52-54.

［3］ 程仕然. 以学科大概念为链的单元教学研究——以人教A版三角函数单元教学为例［J］. 中学数学月刊，2023（04）：12-15+18.

［4］ 徐利花. 基于深度学习优化概念教学——以“事件的独立性”为例［J］. 中学数学杂志，2022（03）：11-15.