核心素养视角下高中数学教材习题与课程标准的一致性研究

［摘 要］ 基于SEC模型，并结合数学学科核心素养相关理论框架，从内容主题和认知水平两个维度对人教A版教材和北师大版教材高中数学教材中的三角函数习题与《普通高中数学课程标准（2017年版2020年修订）（简称课程标准）》进行一致性研究. 研究发现，北师大版教材与课程标准的一致性更高.

［关键词］ 核心素养；一致性研究；教材习题；课程标准

提出问题

《普通高中数学课程标准（2017年版2020年修订）》（简称课程标准）正式提出数学学科核心素养，并将其描述为学生通过数学学习而逐步形成的正确价值观、必备品格和关键能力，具体包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析［1］.

课程标准是教材编写、教学、评估和考试命题的依据，是国家管理和评价课程的基础［2］. 教材作为课程内容的重要载体，其编写需要与课程标准保持一致. 习题作为教材内容的重要组成部分，是教学过程中不可或缺的因素. 一方面，习题是帮助学生掌握知识、提升能力的重要工具；另一方面，习题是教师了解学生的知识掌握情况的重要途径. 余元庆认为习题配备得好不好，直接影响学生的学习质量的高低［3］. 虽然学界对试卷与课程标准有大量的一致性研究［4-7］，但有关教材习题与课程标准的一致性研究较少. 有学者发现，在数学教学实践中，不少教师没有充分挖掘教材中习题的功能，盲目使用教辅［8］. 三角函数是一类最典型的周期函数，提供了对周期性变化的思考，在高中数学教材中占有重要地位［9］.

通过上述多方面的思考，本研究以核心素养为出发点，对现行教材中的三角函数习题与课程标准进行了一致性比较，希望从中发现问题，以便为后续改进提供参考和借鉴.

研究设计

1. 研究对象

鉴于人民教育出版社和北京师范大学出版社2019年出版的普通高中数学教科书（分别简称人教A版教材和北师大版教材）使用范围较广且影响较大，本研究选定这两版教材中的三角函数习题与课程标准进行一致性比较，涉及教材中的“例题”“练习题”“习题”“复习参考题”等版块.

2. 研究工具

John Smithson和Andrew Porter等人在Norman L.Webb的研究基础上开发了SEC一致性分析模型，通常用于判断教学项目与课程标准之间的一致性［10］.

本研究采用SEC模型从内容主题和认知水平两个维度来探讨教材习题和课程标准的一致性程度. 研究过程大致分为三步：

第一，建立“5×3”的二维矩阵. 在内容主题维度上，参照课程标准，将“三角函数”章节划分为“角与弧度”“三角函数的概念与性质”“同角三角函数的基本关系式”“三角恒等变换”和“三角函数的应用”五部分. 在认知水平维度上，根据喻平教授所提的数学核心素养评价框架，划分为知识理解、知识迁移、知识创新三类［11］. 知识理解表现为初步了解、初步体会、感受、认识知识；知识迁移表现为掌握、利用知识，运用多种知识解决复杂问题；知识创新表现为设计不同方法，选择不同知识解决非常规问题［11］.

第二，将二维数据转化为比率分别填入三张二维矩阵表.

第三，利用Porter一致性公式［12］P=1-算出结果. 其中n是二维框架单元格的总数，a表示课程标准矩阵的第i个单元格所对应的数值，b表示教材矩阵的第i个单元格所对应的数值；P为一致性系数，范围在0到1之间，越趋近于1代表一致性越高.

3. 编码方法

分析教材和课程标准时，首先，将三角函数的五个内容主题“角与弧度”“三角函数的概念与性质”“同角三角函数的基本关系式”“三角恒等变换”和“三角函数的应用”分别编码为1，2，3，4，5；其次，将数学抽象、逻辑推理、数学建模、数学运算和直观想象分别编码为A，R，M，O，I（由于“三角函数”章节基本不涉及数据分析素养，所以将其去除）；再者，将知识理解、知识迁移和知识创新分别编码为L1，L2，L3. 在认知水平分布时，可简写为1，2，3，例如A1表示数学抽象知识理解水平.

需要特别说明的是，分析教材时，若一道题有多个小问，则将每一小问记为一道习题，根据已有研究［13］，若一道习题涉及多个核心素养，则编码时只选取其中最主要的两个核心素养.

编码结果

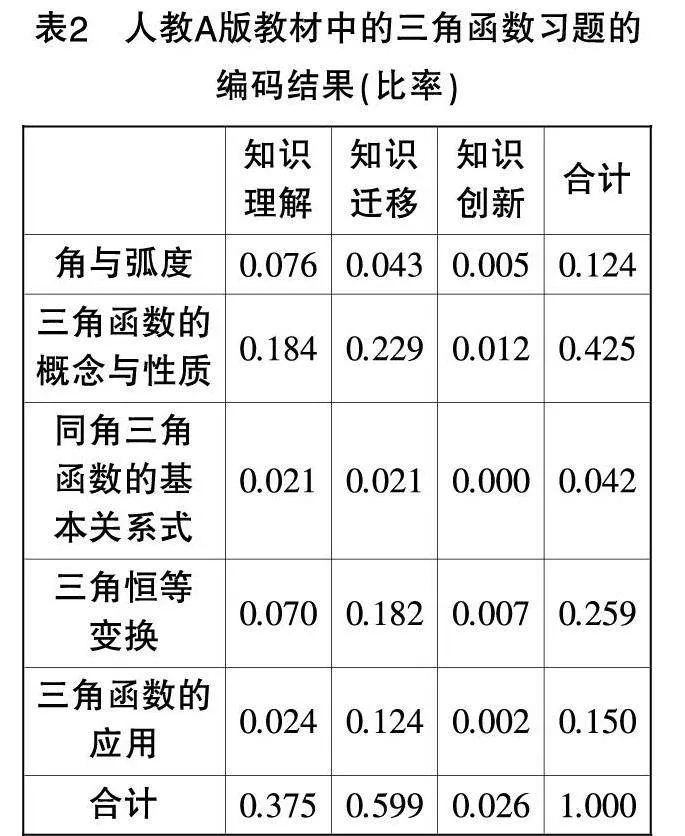
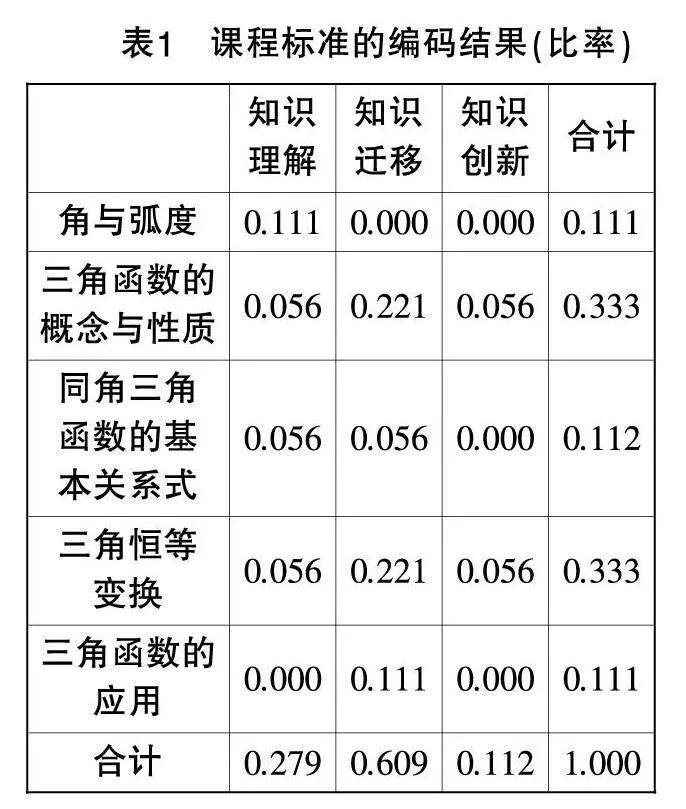
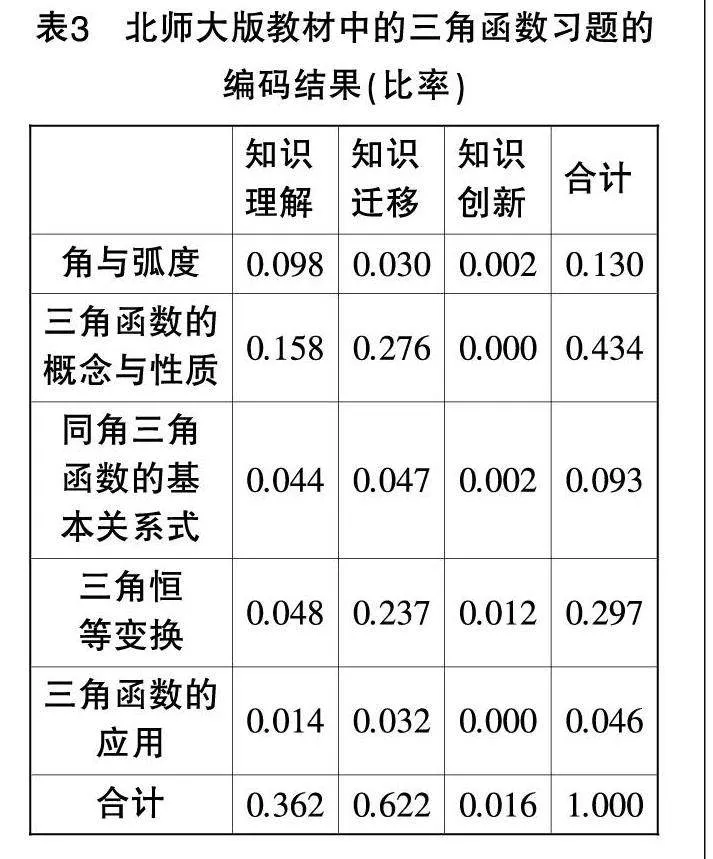
为了减少人工编码的误差，编码工作由两位研究人员独立完成，然后用SPSS26.0软件对编码结果进行Kappa一致性检验，得出Kappa值为0.867，说明编码结果具有良好的一致性，对分歧点进行讨论修改，形成最终一致的编码结果，数据结果见表1至表3.

结果与分析

1. 两版教材中的三角函数习题与课程标准的一致性系数

根据Porter一致性公式，计算人教A版教材和北师大版教材中的三角函数习题与课程标准的P值分别为0.7641，0.7807.Gavin W.Fulmer利用R软件通过随机模拟，得出“5×3”编码标准（30标准点）临界值范围为0.8667～0.9444［14］. 虽然北师大版教材与课程标准的一致性系数略高于人教A版教材与课程标准的一致性系数，但二者均低于临界值下限0.8667，说明两版教材中的三角函数习题与课程标准的一致性程度较弱.

2. 内容主题维度

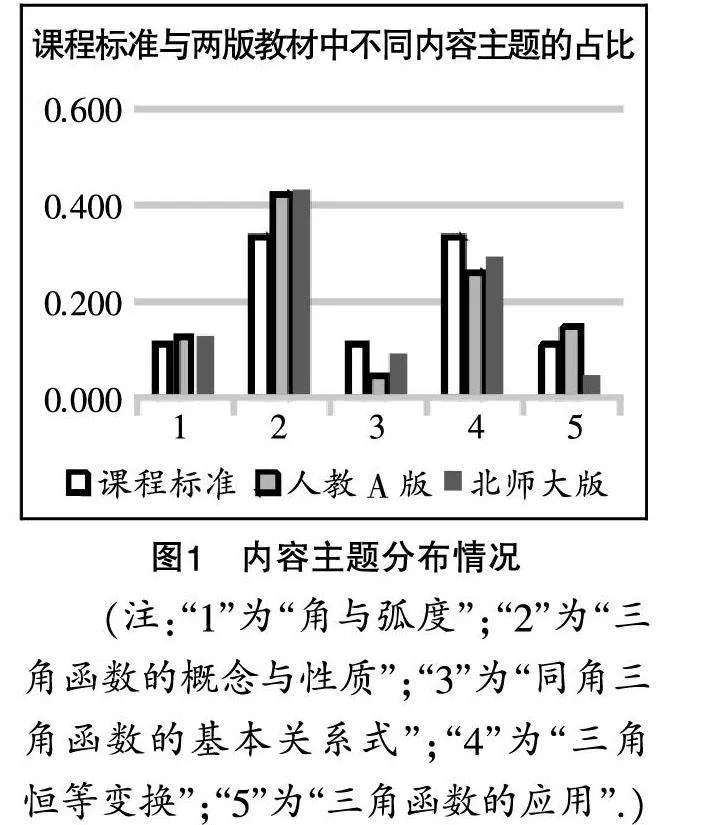
（1）内容主题维度下的两版教材与课程标准之间的差异

由图1可知，总体上课程标准中内容主题的占比为：三角函数的概念与性质=三角恒等变换>角与弧度=同角三角函数的基本关系式=三角函数的应用. 两版教材与课程标准差别不大. 其中，“三角函数的概念与性质”和“三角恒等变换”的占比均超过均值0.2，而“角与弧度”“同角三角函数的基本关系式”和“三角函数的应用”的占比则均在均值0.2之下.

从内容主题来看，对于“三角函数的概念与性质”和“角与弧度”，在两版教材中的占比都高于课程标准，其中人教A版教材更接近课程标准；对于“同角三角函数的基本关系式”和“三角恒等变换”，在两版教材中的占比都低于课程标准，其中北师大版教材更接近课程标准；对于“三角函数的应用”，在人教A版教材中的考察比重高于课程标准，而北师大版教材的考察比重则低于课程标准.

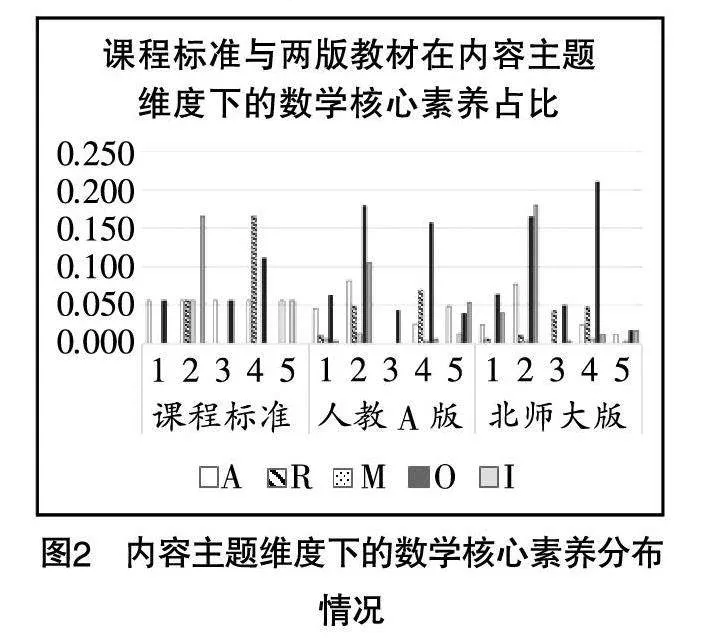
（2）内容主题维度下的数学核心素养分布情况

根据统计后的编码结果得到课程标准、人教A版教材和北师大版教材在内容主题维度下的数学核心素养的分布情况，如图2所示.

由图2可知，在“角与弧度”的维度下，课程标准侧重于培养数学运算和数学抽象；人教A版教材同样如此，但考查数学抽象的比重略小于课程标准，考查数学运算的比重略大于课程标准；相较于课程标准，北师大版教材侧重于培养数学运算的同时，考查直观想象的比重大于数学抽象.在“三角函数的概念与性质”的维度下，课程标准侧重于培养直观想象，同时注重对数学建模、逻辑推理和数学抽象的培养，并未涉及数学运算；而人教A版教材对数学运算的考查比重最大，其次为直观想象，考查数学建模的比重最小，且明显小于课程标准；北师大版教材考查比重最大的核心素养与课程标准相同，均为直观想象，其次为数学运算，数学建模最小，其中直观想象、数学建模的比重明显小于课程标准. 在“同角三角函数的基本关系式”的维度下，课程标准侧重于数学运算和数学抽象的培养；人教A版教材只涉及数学运算的考查；北师大版教材侧重于数学运算和逻辑推理的培养. 在“三角恒等变换”的维度下，课程标准侧重于逻辑推理、数学运算和数学抽象的培养；人教A版教材考查数学运算的比重高于课程标准，考查逻辑推理和数学抽象的比重均低于课程标准，此外，人教A版教材还有较少的关于数学建模和直观想象的考查；北师大版教材考查数学运算的比重明显高于课程标准，考查逻辑推理和数学抽象的比重则均低于课程标准，此外，北师大版教材还考查了直观想象和数学建模. 在“三角函数的应用”的维度下，课程标准侧重于数学建模和数学抽象的培养；人教A版教材在这两项上的考查比重均低于课程标准，另外考查了数学运算和直观想象；北师大版教材对该主题的考查比重较低，且对数学建模和数学抽象的考查比重均低于课程标准.

3. 认知水平维度

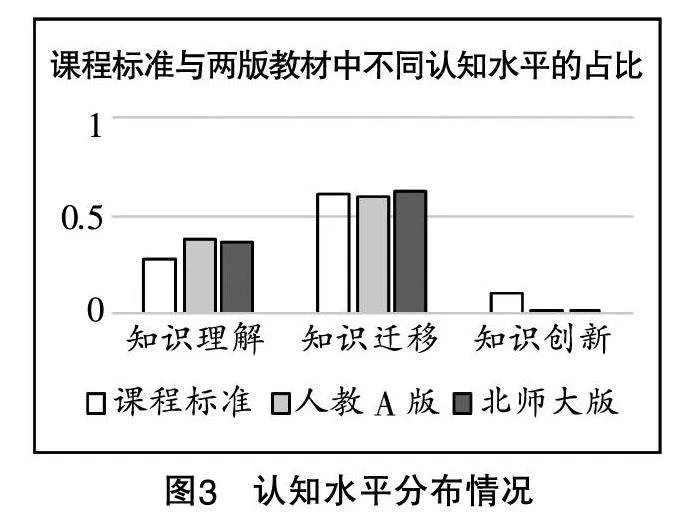
（1）认知水平维度下的两版教材与课程标准之间的差异

由图3可知，对于认知水平的分布，课程标准主要集中在知识迁移，其次是知识理解，最后是知识创新，两版教材也有同样的趋势.对于知识迁移水平，在人教A版教材中的占比低于课程标准，而在北师大版教材中的占比则高于课程标准；对于知识理解水平，在两版教材中的占比均高于课程标准；对于知识创新水平，在两版教材中的占比均远低于课程标准.

（2）认知水平维度下的数学核心素养分布情况

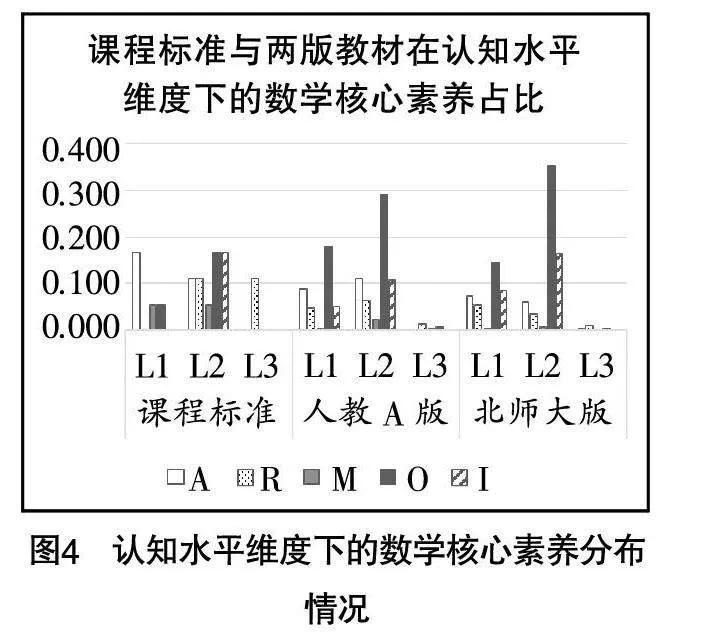
根据统计后的编码结果得到课程标准、人教A版教材和北师大版教材在认知水平维度下的数学核心素养分布情况，如图4所示.

由图4可知，参照课程标准，在认知水平上，两版教材习题的数学核心素养的分布很不均衡.在知识理解上，在课程标准中，数学抽象的占比最多，其次为数学运算和数学建模；在人教A版教材中，数学运算的占比最大，其次为数学抽象，数学建模的占比最小，数学运算的占比大于课程标准，数学抽象和数学建模的占比均小于课程标准；在北师大版教材中，占比最大的依然是数学运算，大于课程标准，数学抽象和数学建模的占比均小于课程标准.在知识迁移上，课程标准对五项核心素养均有所考查，占比最大的是直观想象和数学运算；在人教A版教材中，占比最大的是数学运算，而且明显大于课程标准，但逻辑推理、数学建模和直观想象的占比均小于课程标准；在北师大版教材中，数学运算的占比最大，超过了课程标准两倍. 在知识创新上，课程标准只涉及逻辑推理，两版教材均涉及逻辑推理，且占比均小于课程标准.此外，人教A版教材还涉及数学运算、数学建模和直观想象，北师大版教材涉及数学抽象和数学运算.

结论与建议

通过对课程标准与两版教材的一致性比较，得到如下结论：

根据Porter一致性公式可得，人教A版教材和北师大版教材中的三角函数习题与课程标准的一致性系数均低于临界值下限，两版教材中的三角函数习题与课程标准的一致性不强，北师大版教材比人教A版教材更接近临界值下限.

在内容主题上，人教A版教材与北师大版教材的内容占比与课程标准相差不大，差距基本上都不超过0.1. 两版教材在不同内容主题上的数学核心素养的考查有所不同，在“角与弧度”“同角三角函数的基本关系式”和“三角恒等变换”三个内容主题上，人教A版教材习题对数学核心素养的考查，相较于北师大版教材，更符合课程标准的核心素养要求；在“三角函数的概念与性质”和“三角函数的应用”两个内容主题上，北师大版教材习题对数学核心素养的考查，相较于人教A版教材，更符合课程标准的核心素养要求.

在认知水平上，以课程标准作为参照，两版教材在认识水平维度下的核心素养占比不同. 整体上，课程标准和两版教材对认知水平的考查均是“知识迁移>知识理解>知识创新”，这与课程标准是相吻合的.在知识理解上，课程标准中数学抽象的占比最大，而北师大版教材和人教A版教材是数学运算占比最大. 在知识迁移上，两版教材中数学运算的占比都远超课程标准，但对于直观想象的重视程度存在不足；在知识创新上，课程标准只考查逻辑推理，两版教材对五项核心素养均有考查，北师大版教材对核心素养的考查与课程标准的要求更加一致.

课程标准对核心素养的考查比例适中，但两版教材对三角函数习题的编制都倾向于培养学生的数学运算核心素养，这可能导致学生发展失衡. 在今后教材修订与完善的过程中，可从以下几方面去考虑.

《普通高中数学课程标准（2017年版）》首次提出六大数学核心素养，它们既相互独立，又彼此交融，是一个有机整体. 以课程标准作为参照，人教A版教材和北师大版教材中的三角函数习题对核心素养的考查分布并不均衡，两版教材习题尤其注重培养数学运算，这与课程标准的要求并不一致. 教材代表编写者对课程标准的一种理解，却未必真正代表课程标准的本来含义［15］. 因此，在教材编写过程中，教材习题编写者应仔细研读课程标准，围绕课程标准要求，合理设置对数学核心素养的考查比例，培养和提升学生的数学核心素养. 两版教材中的三角函数习题对数学建模素养和直观想象素养的考查较少，而数学建模素养和直观想象素养都是培养学生数学能力的重要素养，因此建议教材增加培养数学建模和直观想象素养的习题.

长期以来，我国中学生的数学水平在国际上遥遥领先，与多年来我国重视“双基”密不可分. 但在知识创新水平上，两版教材的权重都低于课程标准. 因此，教材应增加一些创新性、开放性习题，引导学生多角度分析问题、解决问题，增强学生的创新意识. 例如北师大版教材第八节中的“水车问题”，要求学生利用所学的三角函数知识建立水车运动模型，并且考虑当河水上涨或旱季河流量减少对数学模型的影响. 这种富有浓厚生活气息，具有开放性、发展性与实践性的习题，结合阅读、写作、建模等实践活动，可为学生的发展搭建平台.

参考文献：

［1］ 中华人民共和国教育部. 基础教育课程改革纲要（试行）［S］. 北京：人民教育出版社，2001.

［2］ 中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［S］. 北京：人民教育出版社，2020.

［3］ 余元庆. 谈谈习题的配备与处理——介绍几本外国中学数学课本中的习题配备［J］. 数学通报，1980（03）：6-10.

［4］ 缪琳，陈清华，苏圣奎. 义务教育课程标准与中考试卷一致性分析——以2013—2016年厦门市中考数学试卷为例［J］. 数学教育学报，2017，26（05）：44-48.

［5］ 徐帆，张胜元，孙庆括. 初中数学学业评价与课程标准的一致性研究——以福建省五套中考数学试卷为例［J］. 数学教育学报，2019，28（03）：98-102.

［6］ 张定强，裴阳. 新高考改革背景下数学试卷与课标一致性研究——以2017—2018年全国Ⅱ卷与浙江卷为例［J］. 数学教育学报，2019，28（04）：55-60.

［7］ 武丽莎，朱立明，王久成. 数学学科核心素养高考测评与课程标准一致性研究——以2019—2021年高考数学Ⅰ试卷为例［J］. 数学教育学报，2022，31（03）：39-44+83.

［8］ 张琥. 新课标高中数学教材习题教学现状分析与建议［J］. 数学教育学报，2012，21（04）：60-63.

［9］ 陈振宣. 三角函数在中学数学中的核心地位［J］. 数学通报，2009，48（06）：25-30.

［10］ 郑蕾，雷浩. 美国“实施课程调查”项目进展及运作机制——SEC项目主任约翰·史密森博士专访［J］. 全球教育展望，2017，46（10）：11-23.

［11］ 喻平. 数学核心素养评价的一个框架［J］. 数学教育学报，2017，26（02）：19-23+59.

［12］ Porter A C. Measuring the Content of Instruction： Uses in Research and Practice［J］. Educational Resear[-]cher，2002，31（07）：3-14.

［13］ 王彦棋，石玲瑜. 基于数学学科核心素养的普通高中数学教科书与课程标准比较分析——以人教A版中的“函数”习题为例［J］. 辽宁师专学报（自然科学版），2021，23（03）：1-7.

［14］ Fulmer G W.Estimating Critical Values for Strength of Alignment Among Curriculum， Assessments， and instruction［J］. Journal of Edu[-]cational and Behavioral Statistics，2011，36（6）：381-402.

［15］ 孔凡哲. 完善基础教育课程标准的若干思路——来自中小学教科书实验的启示［J］. 教育研究，2008，（04）：56-62.