系统设计问题 问道单元教学

［摘 要］ 文章以“用向量法解决三角形问题”为例，探究大单元背景下的问题系统设计与实施，启发学生探索与寻求问题解决路径，引导学生深度思考，促进学生数学学科核心素养的提升.

［关键词］ 单元教学；问题系统；深度学习

单元教学是指从单元整体出发，把相关知识与应用方式关联成一条教与学的线索，形成一个不可分离的教学整体. 对单元教学的实施，需要教师进一步转变教育方式，确立新的教育理念.

单元教学意识的形成需求

《普通高中数学课程标准（2017年版2020年修订）》强调：为促进核心素养的阶段性、持续性发展，应把握教学内容的整体性［1］. 这要求教师以整体研读教材为基础，领会单元教学的主题知识与方法，按照系统设计问题的思路，以实现单元教学目标为前提，开展单元下每一个课时的教学活动，使学生通过单元学习，有效提升数学学科核心素养.

课例研究

以“用向量法解决三角形问题”为例，教学目标为：用向量法证明已学的三角形的性质，以及解决三角形问题，让学生进一步体验向量的工具性作用.

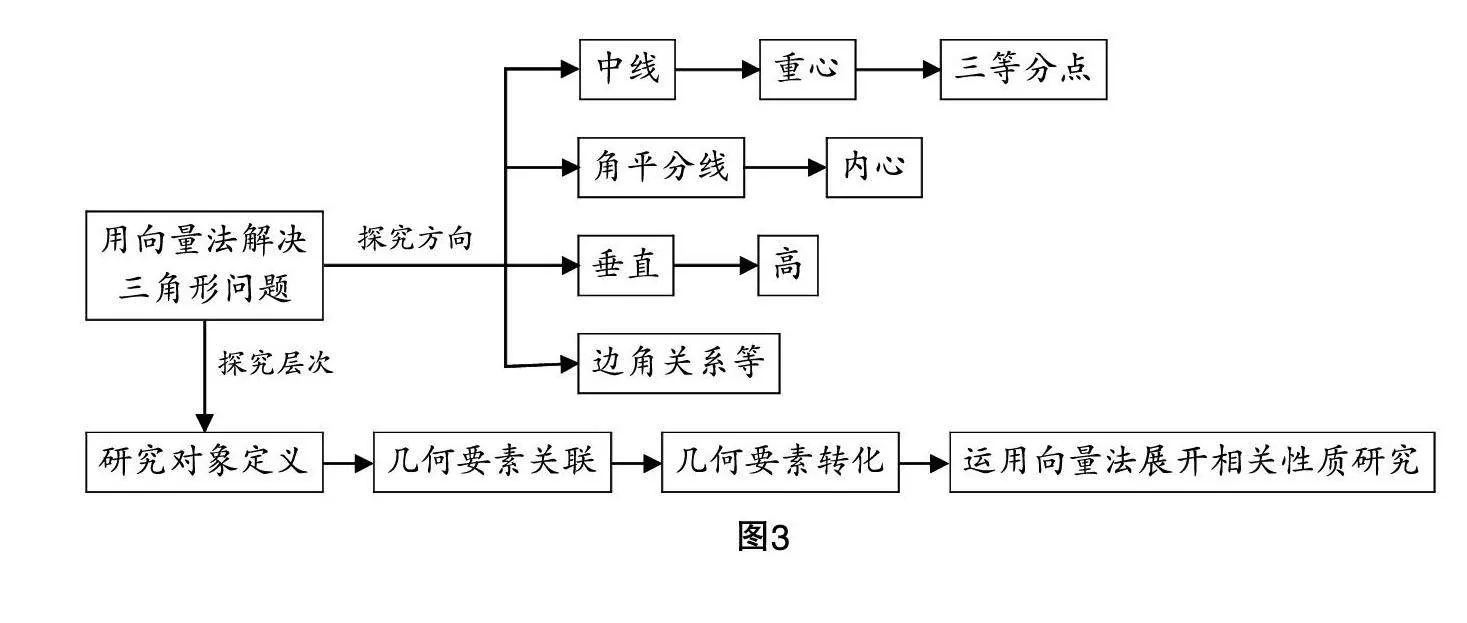
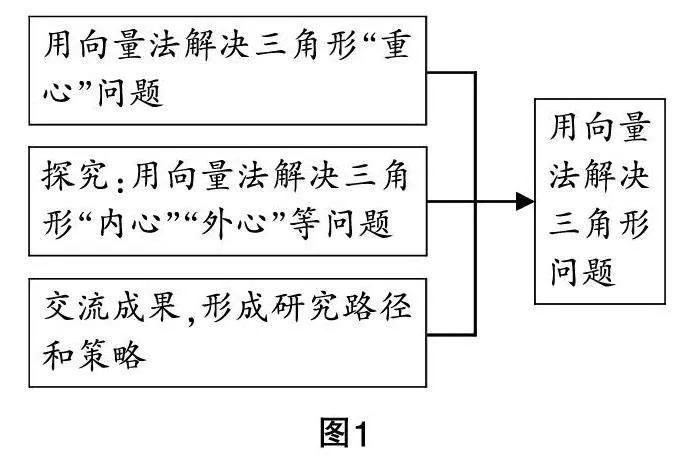
本课例以三角形为探究对象，大致包括以下探究要点：①目标的定义；②几何要素之间的关联与转化；③相关性质的延伸. 探究起点是：用向量法将三角形的重心与三角形的边角关系准确地表达出来. 具体课时安排如图1所示.

本课例承接“正弦、余弦定理及其应用”课程. 在“正弦、余弦定理及其应用”课程中，学生已对三角形的基本要素以及正弦、余弦定理有了较为深刻的印象和使用经验，但是思考正弦、余弦定理形成的过程，是应用向量法的结果，因此“用向量法解决三角形问题”是一个切实可行的探究方向.

三角形的四“心”（重心、内心、外心、垂心）是三角形很重要的基本量，也是学生学习的难点，而向量是“数”与“形”结合的桥梁，它与数学各个方面有着紧密联系，是解决三角形问题的有力工具［2］，因此本课例将重点介绍用向量法解决三角形重心问题，并以其为探究起点，为学生继续用向量法解决三角形外心、内心等问题提供可行的探究路径与思考方式，让学生在完成必修二的学习后能够更有效地运用向量法解决更多有关三角形的问题. 在此过程中，本课例通过设计三角形特性问题，引导学生切实体验用向量法解决三角形问题具有运算与推理兼顾的优势，并通过向量的数形结合的展现，促使学生学会文字语言、符号语言和图形语言之间的相互转化，加深学生对向量法的认识.

本课例的首要任务是通过三角形几何要素与平面向量运算法则的关联探究，对比几何法与向量法的研究路径，架构更合理的研究方式.

1. 问题系统设计

问题系统是指建立在学科素养分析基础上，指向目标、提升学习有效性的问题集合，并且表现为动态的、逻辑化的问题结构. 问题系统的设计目的是尊重学习主体的普适性，结合学习主体已有的学习经验，进一步驱动其主观能动性，明确其探索意向.

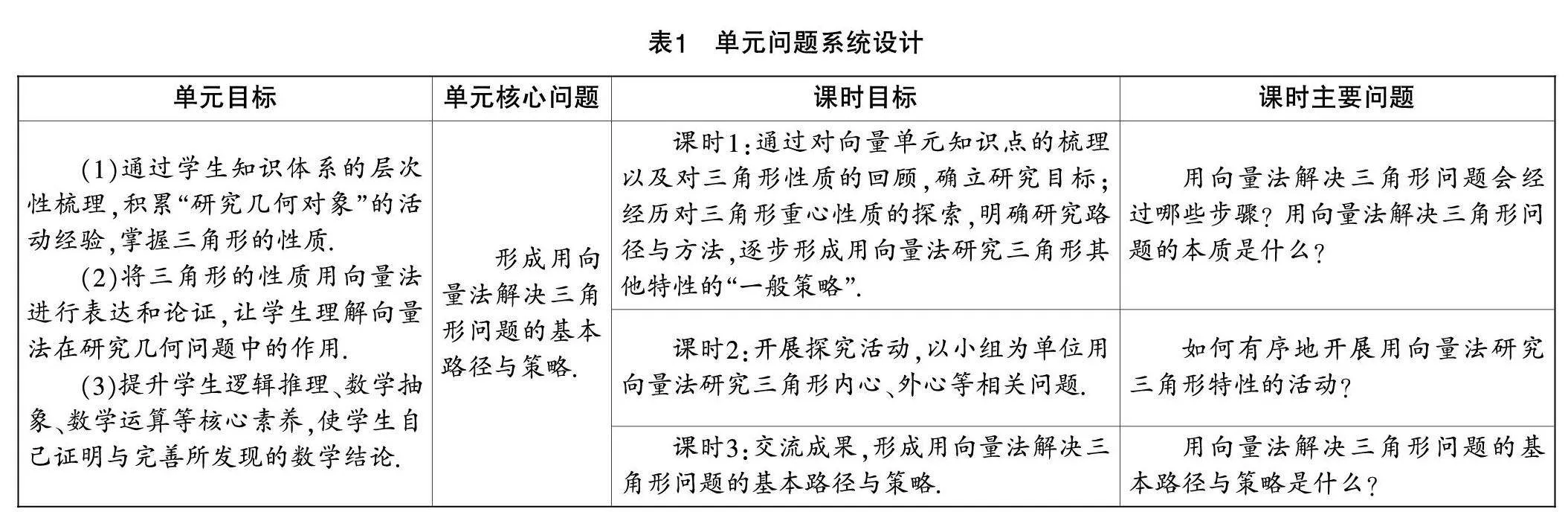
在教学过程中，以问题为导向，使教学目标更加明确，任务更加具体，教学过程更加清晰，有利于学生抓住要旨、教师驾驭课堂［3］. 这里教师应该根据学生的知识结构体系和思维故障点，从教材出发，依据教学重点与难点设计单元问题系统，保证问题环环紧扣、层层递进、步步深入，确保知识的整体性与连贯性，为发展学生的数学学科核心素养提供有力抓手. 以“用向量法解决三角形问题”为例，问题系统设计思路如表1、表2所示（分别为单元问题系统设计和课时问题系统设计）.

以“四何”问题为基础设计课时问题矩阵，可有效规避所提问题的离散与低效；将问题层次进行划分，可帮助学生完善用向量法解决三角形问题的认知结构体系；通过师生互动与生生互动的方式化解认知冲突，可使学生整体把握用向量法解决问题的基本策略.

新课程采用“主线引导主题，指向核心内容”结构展现课程实施内容，故问题链设计的本源在于使学生在单元知识领域下把握主题核心内容，通过探究活动掌握向量这一工具的基本应用方式，在经历抽象、概括、迁移等探究过程后，将用向量法解决三角形问题的基本结构模式纳入已有的知识体系中.

2. 单元思维导图引领与策略总结

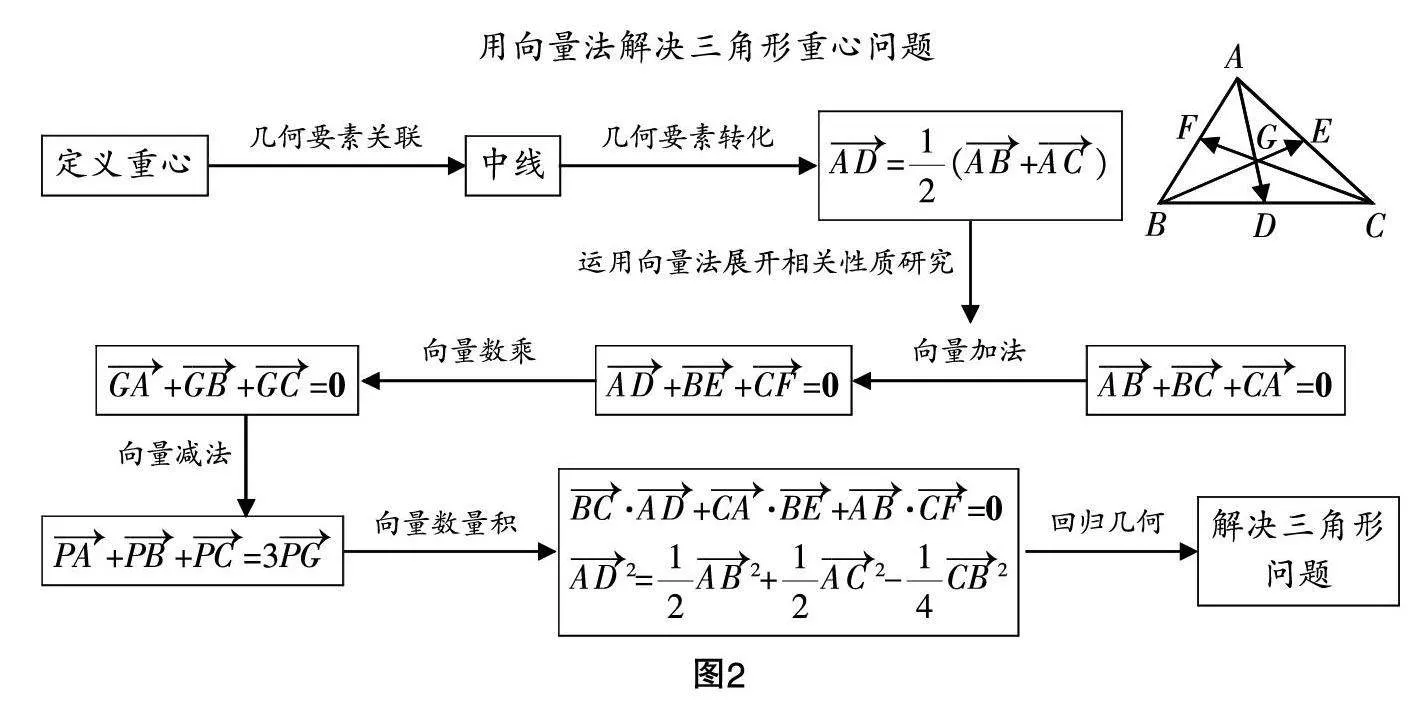
单元教学设计追求：知识的完备性、逻辑的连贯性、思想的统一性、方法的普适性以及思维的系统性. 本节课作为初始探究课程，可以通过思维导图的形式，引导学生整理探究过程，引发学生多角度思考问题. 以本节课为例，探究过程的思维导图如图2所示.

经历上述探究过程，学生对向量和几何之间的关系有了较深刻的认识，也体验到了多维度探索几何问题的方式，提炼了向量法在其他几何问题中的基本应用策略. 例如将平面内的任意一点P转化成空间中的任意一点，引发对空间向量基底的探索与思考，甚至引发对用向量法解决空间立体几何问题的探究，等等. 开放式的主题探究也充分体现了单元教学对培养系统性思维、连贯性逻辑等的要求，为提升学生的思维能力奠定了基石.

另外，经历“探究—综合—整理—提炼”的过程，深入学习“用向量法研究三角形重心问题”的内容之后，引导学生对三角形其他性质进行探究，即在总结主要探究路径的基础上，鼓励学生更加深层次地思考如何用向量法解决三角形的其他性质问题，也就是将“重心”的研究方式进行迁移，为课时2的教学做好铺垫，协助学生架构更完整的思维体系. 本单元教学范例如图3所示.

单元主题内容一般以单元课程内容为基础，让学生把握本单元思想、知识、方法，再到素养的一次深层次提升，这也是数学学习的重要目标. 通过单元主题内容的深度研究，让课堂得到延伸，是培养学生探究精神和创新意识的有效路径. 本节课的总结环节对后续探究方向提出了展望，鼓励学生合情推理、大胆猜想，通过类比与化归等方式进行逻辑推理，体验“再创造”的过程，为单元学习拓展提供新契机.

课例实践后反思

从学科的角度来说，单元主题教学的关键是引导学生有效地进行学科深度学习，而深度学习是教学中的学生学习而不是一般的学习者的自学，必有教师的引导和帮助［4］，这就要求教师在教学过程中改变教学理念，通过教学过程中问题的系统设计，培养学生积极探寻解决问题的有效策略，真正实现学生深度学习. 让学生在关注知识目标的基础上，超越知识表象学习而进入深层次的构造式学习，积累并把握学科知识与研究方法，从而提升学生的基本素养；让学生在深刻理解数学知识的前提下，思维得到充分的训练，智慧得到有效的启迪，从而提升学生的核心素养，实现知识与智慧的转化与升华.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］. 北京：人民教育出版社，2020.

［2］ 赵光辉. 向量与三角形“谈心”［J］. 考试：高考数学版，2011（Z3）：93-94.

［3］ 李志敏. “问题化”数学教学中的“问题设计”［J］. 中学数学教学参考，2016（05）：18.

［4］ 郭华. 深度学习及其意义［J］. 课程·教材·教法，2016，32（11）：23-32.