基于DBO-MPC的混合动力汽车能量管理策略

毛星宇，蒙艳玫，许恩永，赵德平，陈远玲，刘鑫

摘要： 混合动力汽车（hybrid electrical vehicle，HEV）的能量管理策略直接决定了车辆的燃油经济性、驾驶性能和寿命，为解决HEV能量管理策略的最优性与实时行驶工况不确定性之间的矛盾，以混联式HEV为研究对象，提出一种基于模型预测控制（model predictive control，MPC）与蜣螂优化算法（dung beetle optimizer，DBO）的HEV能量管理策略。首先，该策略采用基于堆叠式长短时记忆神经网络（stacked long-short term memory neural network，Stacked LSTM-NN）的车速预测模型预测未来行驶车速。其次，根据预测车速将混合动力汽车的功率分配问题描述为MPC预测范围内的滚动优化问题，提出考虑燃料消耗和电池保护的成本函数，利用DBO算法对预测时域内发动机功率进行优化求解。最后，在城市道路循环（urban dynamometer driving schedule，UDDS）工况下分别对所提策略的车速预测精度和经济性与其他策略进行仿真对比验证。结果表明：与传统LSTM速度预测模型相比，Stacked LSTM速度预测模型的RMSE降低了13.9%，每步平均预测时间减少1 ms；与基于规则的策略相比，基于DBO-MPC的策略模型节油率达到25.3%，同时SOC状态波动更为平稳，对电池的保护效果更好。

关键词： 混合动力汽车；能量管理；控制策略；车速预测

DOI： 10.3969/j.issn.1001-2222.2024.03.009

中图分类号：U469.7文献标志码： B文章编号： 1001-2222（2024）03-0050-08

随着全球汽车数量迅猛增长，环境污染和能源消耗问题变得日趋严重，各国对可持续发展和碳中和的重视程度也越来越高，对汽车进行结构性改革迫在眉睫［1］。在过去的几十年里，人们对新能源汽车，尤其是混合动力汽车（HEV）进行了广泛研究。混合动力汽车作为传统燃油汽车向电动汽车（EV）转变的过渡产物，其对二者的优势进行了融合，既可以纯电动行驶，减少排放，又能有效解决纯电动带来的续航里程焦虑问题。然而，混合动力汽车的多源动力系统引发了与能量管理相关的问题，这也成为了过去十年研究的焦点之一［2-6］。

目前，针对HEV能量管理策略（EMS）的研究主要分为基于规则的EMS和基于优化的EMS两类。基于规则的EMS因其控制简单且稳定，被引入插电式混合动力汽车以提高发动机效率［7］。但其对驾驶循环的适应性较差，并且由于设定目标单一，系统参数固定，难以达到最佳的整体性能。基于优化的EMS则以动态规划算法（DP）［8］和庞特里亚金极小值原理（PMP）［9］为代表。混合动力系统的最佳能量管理问题实际上是一个多阶段控制问题。相对于其他优化算法，DP算法更适合解决多阶段决策的最优化问题［10］。在实际行驶过程中，基于全局优化的EMS虽然可以实现最优的整体性能，但其计算成本高，且需预知整个工况信息，导致其难以在线应用。而模型预测控制（MPC）通过在线预测车辆未来短期车速，将全局最优控制转变为基于预测时域的局部最优控制，可以采用不同种类的优化算法以实现对预测时间窗口内的最优化问题的连续迭代求解，从而使MPC成为EMS的一种有效应用［11］。魏丽青等［12］提出了一种基于组合预测模型的速度预测模型，并以燃油经济性最优为目标，建立基于MPC的控制策略，该策略显著提高了车速预测精度与燃油经济性。He等［13］提出了分层MPC-EMS与深度确定性策略梯度算法相结合的插电式混合动力公交车能量管理策略，通过上层控制器和下层MPC生成的SOC轨迹，再根据深度神经网络的预测信息快速求解目标方程，有效降低了公交车的油耗。

为提高在线预测的精确性并减小HEV的燃料消耗，本研究结合模型预测控制和蜣螂优化算法（DBO），提出一种基于DBO-MPC的混合动力汽车能量管理策略。首先，采用基于Stacked LSTM的速度预测模型预测未来行驶车速；其次，根据预测车速将混合动力汽车的功率分配问题描述为MPC预测范围内的滚动优化问题，提出考虑燃料消耗和电池保护的成本函数，利用DBO算法对预测时域内发动机功率进行优化求解，并使用UDDS工况数据对此策略进行仿真验证。

1HEV动力模型建模

研究对象为混联式HEV，其结构简图见图1，由发动机、离合器、电池、电机、耦合机构、变速箱等组成。在混联HEV的驱动系统中，发动机和两个电机通过行星齿轮组连接，行星齿轮组由一个太阳齿轮、一个齿圈、一个行星齿轮架和几个小齿轮组成。其中，主驱动电机MG1、发电机MG2、发动机分别与行星齿轮机构中的齿圈、太阳轮、行星架相连，耦合机构作为结构的核心部件，可以实现发动机转速和扭矩的解耦以及发动机与两台电机的功率分配。整车及动力部件参数见表1。

1.1车辆纵向动力学模型

利用纵向力平衡方程式（1），能够推导出运行过程中动力系统需要提供给车辆的驱动力。

Ft=Ff+Fw+Fi+Fj

Ff=Gfcosi

Fw=CDA21.15ua2

Fi=Gsini

Fj=δmdudt。（1）

式中：Ft为车辆所需驱动力；Ff为滚动阻力；Fw为空气阻力；Fi为坡度阻力；Fj为加速阻力；G为车辆重力；f为滚动阻力系数；i为道路坡度；CD为空气阻力系数；A为车辆迎风面积；ua2为车速；δ为车辆旋转质量系数；m为车辆质量；du/dt为车辆行驶加速度。

1.2耦合机构模型

耦合机构是混合动力系统实现发动机转速、扭矩与路载双解耦的核心部件，各动力源部件与行星齿轮配合从而实现自动变速。在行星齿轮中，齿圈、太阳轮及行星架之间转速和扭矩的关系［14-15］如下：

Rrωr+Rsωs=（Rr+Rs）ωp，（2）

Rr+RsRrTr=Tp=Rr+RsRsTs。（3）

式中：Rr为齿圈的半径；Rs为太阳轮的半径；ωr为齿圈角速度；ωs为太阳轮角速度；ωp为行星架角速度；Tr为齿圈扭矩；Ts为太阳轮扭矩；Tp为行星架扭矩。

1.3发动机模型

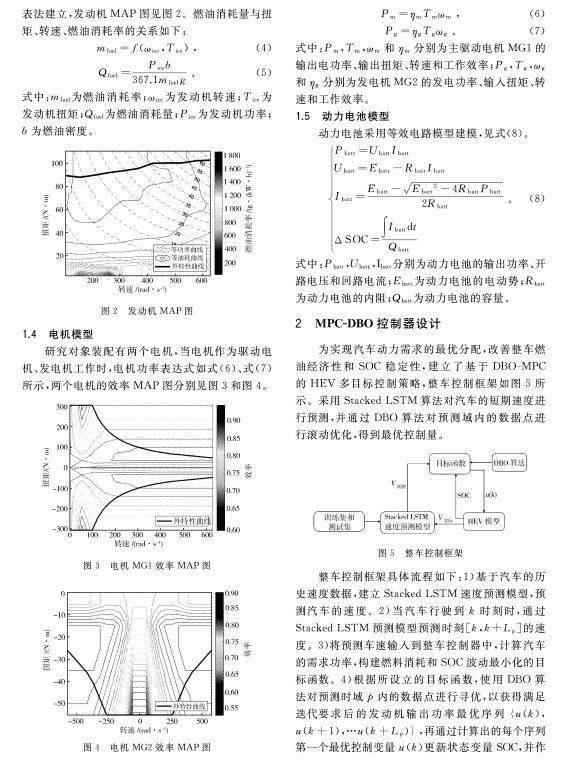
由于发动机在工作时具有显著的非线性，难以建立准确的仿真模型，因此发动机油耗模型通过查表法建立，发动机MAP图见图2。燃油消耗量与扭矩、转速、燃油消耗率的关系如下：

mfuel=f（ωice，Tice），（4）

Qfuel=Piceb367.1mfuelg。（5）

式中：mfuel为燃油消耗率；ωice为发动机转速；Tice为发动机扭矩；Qfuel为燃油消耗量；Pice为发动机功率；b为燃油密度。

1.4电机模型

研究对象装配有两个电机，当电机作为驱动电机、发电机工作时，电机功率表达式如式（6）、式（7）所示，两个电机的效率MAP图分别见图3和图4。

Pm=ηmTmωm，（6）

Pg=ηgTgωg。（7）

式中：Pm，Tm，ωm和ηm分别为主驱动电机MG1的输出电功率、输出扭矩、转速和工作效率；Pg，Tg，ωg和ηg分别为发电机MG2的发电功率、输入扭矩、转速和工作效率。

1.5动力电池模型

动力电池采用等效电路模型建模，见式（8）。

Pbatt=UbattIbatt

Ubatt=Ebatt－RbattIbatt

Ibatt=Ebatt－Ebatt2－4RbattPbatt2Rbatt

ΔSOC=∫IbattdtQbatt。（8）

式中：Pbatt，Ubatt，Ibatt分别为动力电池的输出功率、开路电压和回路电流；Ebatt为动力电池的电动势；Rbatt为动力电池的内阻；Qbatt为动力电池的容量。

2MPC-DBO控制器设计

为实现汽车动力需求的最优分配，改善整车燃油经济性和SOC稳定性，建立了基于DBO-MPC的HEV多目标控制策略，整车控制框架如图5所示。采用Stacked LSTM算法对汽车的短期速度进行预测，并通过DBO算法对预测域内的数据点进行滚动优化，得到最优控制量。

整车控制框架具体流程如下：1）基于汽车的历史速度数据，建立Stacked LSTM速度预测模型，预测汽车的速度。2）当汽车行驶到k时刻时，通过Stacked LSTM预测模型预测时刻［k，k+Lp］的速度。3）将预测车速输入到整车控制器中，计算汽车的需求功率，构建燃料消耗和SOC波动最小化的目标函数。4）根据所设立的目标函数，使用DBO算法对预测时域p内的数据点进行寻优，以获得满足迭代要求后的发动机输出功率最优序列｛u（k），u（k+1），…u（k+Lp）｝，再通过计算出的每个序列第一个最优控制变量u（k）更新状态变量SOC，并作用于前文所建立的HEV模型中。5）车辆进入第k+1时刻，重复第k时刻的动作，直到行驶状态结束。

2.1基于Stacked LSTM的速度预测

传统RNN在记忆之前的长序列时很难给出准确的预测。因此，引入LSTM（long-short term memory） RNN架构［16］来解决传统RNN的这一问题。LSTM架构在其隐藏层中有一个基本单元，称为内存块。 LSTM的内存块有一个或多个内存单元，此外还有3个门（输入门、输出门和遗忘门）。根据LSTM架构，计算LSTM存储单元隐层的运算（如图6所示），并在每个时间步长t下更新，如式（9）所示：

ft=σ（WfhHt－1+WfxXt+bf）

it=σ（WihHt－1+WixXt+bi）

Ct′=tanh（WchHt－1+WcxXt+bc）

Ct=it⊙Ct′+ft⊙Ct－1

Ot=σ（WohHt－1+WoxXt+bo）

Ht=tanh［Ct］⊙Ot。（9）

式中：ft为 t 时刻的遗忘门，控制从上一时刻进入的状态变量Ct－1中遗忘的信息数量；it为t时刻的输入门，控制保存t时刻Ct′的信息数量；Ct′为t 时刻的候选状态变量，实现选择性通过信息的功能；Ct为t时刻 LSTM 内部的状态变量；Ot为t时刻的输出门，控制向外部状态Ht输出t时刻Ct的信息数量；σ为sigmoid 计算模块；tanh为tanh计算模块；Ht－1为t－1时刻的外部状态变量；Ht为t时刻的外部状态变量；W为各个门的权重；b为各个门的偏差；ε为Hadamard积，即两个相同维度矩阵对应元素相乘产生另一个新的相同维度矩阵的运算。

在本研究提出的方法中，将构建一个Stacked LSTM模块的深度网络，用于预测未来车速。Stacked LSTM有以下两个优势：1）Stacked LSTM层使模型能够在每个时间步从不同方面学习原始时间信号的特征；2）模型参数分布在模型的整个空间，不增加内存容量，使模型能够加速收敛，细化原始数据的非线性运算。本研究中Stacked LSTM网络主要由4个LSTM层组成，如图7所示。首先，输入层将窗口大小为L=10的一维序列作为输入，再将其输入馈送到Stacked LSTM网络的第一个LSTM层，输入层隐藏单元的大小等于输入序列窗口的大小L。第一个LSTM层馈送到第二个LSTM层，依此类推，上一层的输出即为下一层的输入。4个LSTM层均有50个隐藏单元。最后，LSTM层馈入只有一个神经元的全连接层，输出时间步长为10的预测车速序列，全连接层的激活函数为线性激活函数。采用均方根误差（RMSE）作为此预测模型的损失函数：

R（k）=∑Li=1（vp（k+i）－v（k+i））2/L，（10）

R=∑Sk=1R（k）2/S。（11）

式中：v（k+i）为第k+i时刻的实际速度；vp（k+i）为k+i时刻的预测速度；R（k）为预测时域L在k时刻的均方根误差；R为整个驾驶周期的均方根误差。

2.2基于BDO算法的多目标优化

Jiankai Xue等［17］于2022年提出了一种新的群体智能优化算法——蜣螂优化算法（dung beetle optimizer，DBO），该算法同时兼顾全局搜索和局部开发，具备快速收敛和高精度求解的优势。

DBO算法对蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为进行模仿来搜索数值范围内的最佳参数。其实现概述如下：1）设置最大迭代次数、蜣螂种群数量等参数，并在搜索空间中随机初始化每只蜣螂个体的位置；2）每次迭代后，不同的蜣螂根据自己的更新规则更新自己的位置，比较所有蜣螂的适应值，记录当前迭代时间下最优蜣螂的信息；3）重复上述步骤，直到满足终止条件，输出全局最优蜣螂个体信息。DBO算法流程图见图8。其各个行为的位置更新公式如下。

1） 滚球行为

滚球行为的更新公式如下：

xt+1i=xti－α×k×xt－1i+b×Δx

Δx=｜xti－xworst｜。（12）

式中：t为当前迭代次数；xti为第i只蜣螂在第t次迭代时的位置信息；k∈（0，0.2］表示挠度系数，为定值；b为属于（0，1）的定值；α为自然系数，赋值为－1或1；xworst表示全局最差位置；Δx用于模拟光强的变化。

2） 跳舞行为

跳舞行为的更新公式如下：

xt+1i=xti+tan（θ∈［0，π］）｜xti－xt－1i｜。（13）

式中：｜xti－xt－1i｜为第i只蜣螂第t和t－1次迭代之间的差异。因此蜣螂位置的更新与当前和历史信息密切相关。

3） 繁殖行为

繁殖行为的更新公式如下：

xt+1i=X*－b1×（xti－Lb*）+b2×（xti－Ub*）， （14）

Lb*=max（X*×（1－R），Lb）， （15）

Ub*=max（X*×（1+R），Ub）。（16）

式中：xti为第i个卵球在第t次迭代的位置信息；b1和b2为两个独立的大小为1×dim维的随机向量；X*表示当前局部最优位置；Lb*和Ub*分别为产卵的下界和上界；R=1－tmaxiter，maxiter为最大迭代次数；Lb和Ub分别为优化问题的下界和上界。

4） 觅食行为

觅食行为的更新公式如下：

xt+1i=xti+C1×（xti－Lbb）+C2×（xti－Ubb），（17）

Lbb=max（Xb×（1－R），Lb），（18）

Ubb=max（Xb×（1+R），Ub）。（19）

式中：xti为第i个蜣螂在第t次迭代的位置信息；C1为服从正态分布的随机数；C2为（0，1）范围内的随机向量；Xb表示全局最优位置；Lbb和Ubb分别为最佳觅食区域的下界和上界。

5） 偷窃行为

偷窃行为的更新公式如下：

xt+1i=Xb+S×g×（｜xti－X*｜+｜xti－Xb｜。（20）

式中：xti为第i个蜣螂小偷在第t次迭代的位置信息；g为大小为1×dim维的服从正态分布的随机向量；S为常数。

将DBO算法嵌入到MPC模型控制器中，目的是对整车的燃料消耗和SOC稳定性两个目标进行优化，并选择发动机输出功率为优化参数。采用DBO算法时，设定蜣螂种群数量为30只，算法最大迭代次数为100次，每个蜣螂都被视为给定搜索空间中的一个点和一个可行的解决方案，它根据自身的变化规律，不断迭代更新自己的位置，减小目标函数的值。

系统的目标函数如式（21）所示：

J=∫tft0αmfuel+βPbat3 600+γ（SOCref－SOC）2dt。（21）

式中：α为燃料的成本价格；β为电价；γ为SOC惩罚因子［18-19］。

以电池SOC作为系统的状态变量，发动机功率作为系统的控制变量，构造的状态转换方程如式（22）所示：

xk+1=f（xk，uk）

xk=SOC（k）

u（k）=Peng（k）。（22）

式中：xk为系统状态变量；uk为系统控制变量。

最优控制应满足以下约束条件：

0≤SOC（k）≤1

0≤neng（k）≤neng_max

Peng_min≤Peng（k）≤Peng_max

0≤Teng（neng（k））≤Teng_max（neng（k））

nmot_min≤nmot（k）≤nmot_max

Tmot_min（nmot（k））≤Tmot（nmot（k））≤

Tmot_max（nmot（k））

Ibat_max_char（k）≤Ibat（k）≤Ibat_max_disch（k）。（23）

式中：neng为发动机转速；Peng为发动机功率；Teng为发动机扭矩；nmot为电机转速；Tmot为电机扭矩；Ibat为动力电池电流。

3分析与讨论

在Python环境下构建基于Stacked LSTM神经网络的短期车速预测模型，并调用采集到的工况数据进行训练和车速预测。此外，本研究也在Python环境下搭建MPC框架，该框架利用速度预测模型提供的实时预测车速进行仿真试验。仿真试验在一台配备Intel（R） Core（TM） i5-10200H CPU @ 2.40 GHz处理器和16 GB运行内存的电脑上运行。

3.1速度预测模型有效性分析

针对车辆实际行驶环境复杂多变的特点，该模型的训练集数据通过实际车辆在南宁道路工况下采集得到，包括拥堵路段、城区和高速公路等不同工况。经过降噪和数据处理后的训练集如图9所示，测试集则采用UDDS工况（如图10所示）。为验证基于Stacked LSTM速度预测模型的有效性，选取传统LSTM速度预测模型与该模型进行对比试验。两个速度预测模型的预测时域范围为10 s，从历史车速数据集中选取当前时刻t前10 s的车速数据作为输入。图11示出两个速度预测模型对UDDS工况的短期预测结果。图12示出两个速度预测模型的均方根误差在预测时域的分布。由图知，在一些速度突变的数据点，两个模型的均方根误差均有些偏高，这是因为速度预测模型主要通过历史车速进行预测，当车速急剧变化时预测精度则会变低。但相对于传统LSTM模型，Stacked LSTM算法学习能力提高，在一定程度上可以降低速度突变带来的影响，并且可以看出，在整个驾驶工况中，Stacked LSTM速度预测模型的均方根误差要比传统LSTM速度预测模型低，经过计算，Stacked LSTM速度预测模型的均方根误差为2.622 0 km/h，传统LSTM速度预测模型的均方根误差为3.044 2 km/h。同时，在实时性方面，Stacked LSTM速度预测模型每步平均预测时间为3 ms，而传统LSTM速度预测模型为4 ms，满足实时运行的要求。因此，Stacked LSTM速度预测模型对行驶工况的短期速度实时预测是有效的。

3.2整车经济性分析

为了验证所提出策略的优越性，建立了基于规则的模型和全局最优DP模型，并在基于速度预测模型所预测的实车工况车速下对三种策略进行比较。设定3种策略的SOC初始值均为0.55，仿真结果见图13至图16。由表2和图14可知，基于规则的策略模型在整个行驶工况中发动机起动频繁且输出功率最大，油耗最高，100 km燃油消耗量达到4.667 5 L，与之相比，基于DBO-MPC的策略模型和基于DP的策略模型相对合理地使用动力电池提供需求功率，其发动机输出功率较低且平稳，DP策略模型的发动机使用频率相对较少，油耗最低，相比基于规则的策略节油率达到了30.6%，基于DBO-MPC策略模型节油效果也比较明显，相比基于规则的策略节油率达到25.3%。电量消耗方面，由图13可知，DP策略模型初始阶段大量使用电池提供能量，电池电量消耗较快，充电后SOC状态依然不够稳定，且末期对电池大量充电也会对电池造成损耗；基于规则策略模型的电池大部分时间处于充电状态，中期经历连续放电，整个行驶周期电池SOC状态波动较大。而基于DBO-MPC的策略模型SOC状态全程较为稳定，避免连续或急速充放电对电池造成的损耗。

4结束语

提出了一种基于DBO-MPC的HEV能量管理策略。建立了基于Stacked LSTM的车速预测模型对未来车速进行短期预测，再以整车燃料消耗量最低与行驶过程电池SOC平衡为目标，采用DBO算法对预测时域内发动机的功率分配进行优化求解，得到最优控制序列。仿真结果表明：基于Stacked LSTM的车速预测模型比传统LSTM预测模型的RMSE 降低了13.9%；基于DBO-MPC策略模型的燃油消耗量比基于规则策略模型节省了25.3%，SOC轨迹也更为平稳，验证了所提策略的有效性。

参考文献：

［1］LIAN R，PENG J，WU Y，et al.Rule-interposing deep reinforcement learning based energy management strategy for power-split hybrid electric vehicle［J/OL］.Energy，2020，197：117297.

［2］WANG B，XU J，CAO B，et al.A novel multimode hybrid energy storage system and its energy management strategy for electric vehicles［J/OL］.Journal of Power Sources，2015，281：432-443.

［3］ZHANG S，XIONG R，CAO J.Battery durability and longevity based power management for plug-in hybrid electric vehicle with hybrid energy storage system［J/OL］.Applied Energy，2016，179：316-328.

［4］CASTAINGS A，LHOMME W，TRIGUI R，et al.Comparison of energy management strategies of a battery/supercapacitors system for electric vehicle under real-time constraints［J/OL］.Applied Energy，2016，163：190-200.

［5］CHEN Z，XIA B，YOU C，et al.A novel energy management method for series plug-in hybrid electric vehicles［J/OL］.Applied Energy，2015，145：172-179.

［6］Dehghani N L，Mohammadi Darestani Y，Shafieezadeh A.Optimal Life-Cycle Resilience Enhancement of Aging Power Distribution Systems：A MINLP-Based Preventive Maintenance Planning［J/OL］.IEEE Access，2020，8：22324-22334.

［7］Banvait H，Anwar S，Chen Y.A rule-based energy management strategy for Plug-in Hybrid Electric Vehicle （PHEV）［C/OL］//2009 American Control Conference.St.Louis：［s.n.］，2009.

［8］顾琰浩，吴晓东，许敏.增程式电动车自适应工况辨识策略研究［J］．车用发动机，2021（1）：1-8.

［9］张新亮，周童.基于双模式优化算法的并联混合动力汽车能量管理策略研究［J］．车用发动机，2020（6）：48-52.

［10］韦超毅，吴雨轮，林长波，等.基于行驶工况识别的混合动力货车能量管理策略［J］．陕西科技大学学报，2022，40（4）：158-164.

［11］张风奇，胡晓松，许康辉，等.混合动力汽车模型预测能量管理研究现状与展望［J］．机械工程学报，2019，55（10）：86-108.

［12］魏丽青，万幸.插电式混合动力汽车车速预测及能量管理策略［J］．车用发动机，2022（3）：69-75.

［13］HE H，HUANG R，MENG X，et al.A novel hierarchical predictive energy management strategy for plug-in hybrid electric bus combined with deep deterministic policy gradient［J/OL］.Journal of Energy Storage，2022，52：104787.

［14］ZENG X，CUI H，SONG D，et al.Jerk Analysis of a Power-Split Hybrid Electric Vehicle Based on a Data-Driven Vehicle Dynamics Model［J/OL］.Energies，2018，11（6）：1537.

［15］崔皓勇.混联式两档AMT客车模式切换协调控制研究［D］．长春：吉林大学，2019.

［16］HOCHREITER S，SCHMIDHUBER J.Long Short-Term Memory［J/OL］.Neural Computation，1997，9（8）：1735-1780.

［17］XUE J，SHEN B.Dung beetle optimizer：a new meta-heuristic algorithm for global optimization［J］．The Journal of Supercomputing，2023，79（7）：7305-7336.

［18］霍志伟.基于预测控制的混联式插电混合动力汽车能量管理策略研究［D］．重庆：重庆理工大学，2022.

［19］LI J，WU X，XU M，et al.A real-time optimization energy management of range extended electric vehicles for battery lifetime and energy consumption［J/OL］.Journal of Power Sources，2021，498：229939.

Energy Management Strategy of Hybrid Electric Vehicle Based on DBO-MPC

MAO Xingyu1，MENG Yanmei1，XU Enyong2，3，ZHAO Deping3，CHEN Yuanling1，LIU Xin1

（1.College of Mechanical Engineering，Guangxi University，Nanning530004，China;2.School of Mechanical Science and Engineering，Huazhong University of Science and Technology，Wuhan430074，China;3.Dongfeng Liuzhou Motor Co.，Ltd.，Liuzhou545005，China）

Abstract： The energy management strategy of hybrid electric vehicle（HEV） directly determines the fuel economy， driving performance and life of vehicle. In order to solve the contradiction between the optimal energy management strategy of HEV and the uncertainty of real-time driving conditions， the energy management strategy of HEV based on model predictive control（MPC） and Dung beetle optimizer（DBO） was proposed based on the research object of hybrid HEV. First， the strategy used the vehicle speed prediction model to predict future driving speed based on stacked long-short term memory neural network（Stacked LSTM-NN）. Then， according to the predicted vehicle speed， the power distribution problem of HEV was described as a rolling optimization problem within the MPC prediction range. Considering the cost function of fuel consumption and battery protection， the DBO algorithm was used to optimize the engine power in the forecast time domain. Finally， under urban dynamometer driving schedule（UDDS） conditions， the speed prediction accuracy and fuel economy of proposed strategy were simulated and compared with other strategies. Compared with the traditional LSTM speed prediction model， the RMSE of Stacked LSTM speed prediction model reduces by 13.9%， and the average prediction time of each step reduces by 1 ms. Compared with the rule-based strategy， the fuel saving rate of DBO-MPC strategy model reached 25.3%， and the SOC state is more stable and the battery protection effect is better.

Key words： hybrid electric vehicle;energy management;control strategy;vehicle speed prediction

［编辑： 袁晓燕］