深度学习视角下的初中数学大单元教学策略研究

【摘要】文章以人教版数学九年级上册“圆”的教学为例，从设计问题链、开展探究活动、迁移所学知识、构建评价体系等多个维度提出深度学习视角下初中数学大单元教学的路径，以期为初中数学教学改革提供理论支撑和实践指导。

【关键词】深度学习；初中数学；大单元教学；教学实践

作者简介：李启艺（1990—），男，福建省厦门集美中学附属滨水学校。

《义务教育数学课程标准（2022年版）》强调教学设计应从关注课时转变为注重单元整体教学。这种转变旨在揭示数学知识间的内在联系以及学习内容与核心素养之间的逻辑关系。近年来，深度学习逐渐成为教育领域的热门话题，其强调学生对知识的理解和应用，关注学生高阶思维的培养。大单元教学策略作为一种新兴的教学方式，为实现深度学习提供了新的思路。具体而言，教师需要以单元为教学核心，紧密联系各个教学环节，围绕深度学习理念开辟大单元教学新路径，引导学生开展深度探索，逐渐由浅层次学习走向深层次学习。

笔者以人教版数学九年级上册第二十四章“圆”的教学为例，阐述深度学习视角下初中数学大单元教学的实施策略。

一、设计“问题之链”，明确大单元教学方向

设计问题链是大单元教学的基础和前提。问题作为单元教学的核心，是学生学习的动力源泉。大单元概念并非具体的知识，而是知识的抽象和概括，它能连接不同的知识层次，使学生更容易理解和吸收知识。为了让学生了解单元大概念，教师需要将大概念分解成一系列问题，将单元知识有机地串联起来，形成问题链。在问题链的引导下，学生能够通过自主探索和合作学习等方式，根据单元中的关键知识，寻找问题的答案，从而进行深度思考。这个过程有助于学生理解单元的重难点知识，探究知识之间的逻辑关系，逐步提炼大单元概念［1］。

在深度学习视角下，初中数学大单元教学策略的实施需要教师充分理解教材，把握学科本质，将大概念转化为具体、可操作的问题链。这一章涉及圆的基本性质，点和圆、直线和圆、圆和圆的位置关系等内容［2］。为了使学生深入理解这些内容，教师可以构建以下问题链：1.什么是圆？如何用数学语言描述圆的基本性质？2.点和圆的位置关系有哪些？如何判断一个点是否在圆上？3.直线和圆的位置关系有哪些？如何判断一条直线是否与圆相切？4.圆和圆的位置关系有哪些？如何判断两个圆是否相切或相交？这一系列问题能够将“圆”这一大概念分解为具体的知识点，引导学生深入思考。在问题链的引导下，学生能够通过多维探索、实践互动、合作交流等，逐步掌握“圆”这一单元的重点与难点，自主构建知识间的逻辑联系。

二、遨游“探索之海”，探究大单元教学内容

（一）开展探究活动，推开探究之门

在大单元教学模式下，教师需要关注学生的学习过程，鼓励学生积极参与探究活动。教师应明确核心素养培养目标和课时教学目标，利用“探究链”确定学习主题，提高教学内容的关联性和完整性，确保学生在探究活动中构建清晰的认知结构，逐渐提升探究能力和综合素养。接着，教师应创设丰富的教学情境，设计形式多样的探究活动，提高学生的学习兴趣和参与度。值得注意的是，在这一环节，教师需要关注学生的思维发展，通过有效的引导，帮助学生克服探索过程中的困难。

这一章节内容丰富，知识点较多。在大单元教学中，教师可以基于核心素养，利用“探究链”确定以下学习主题：1.圆的有关性质，包括圆的定义、圆周率、圆的对称性等；2.点和圆、直线和圆的位置关系，包括点和圆的位置关系、直线和圆的位置关系等［3］；3.正多边形和圆，包括正多边形的定义、正多边形和圆的关系等；4.弧长和扇形面积，包括弧长的计算、扇形面积的计算等。在这一基础上，教师可以探究情境为基石，以探究活动为载体，注重教学内容的内在联系，助力学生在深度探索的过程中构建清晰的知识体系。例如，在讲解“圆的有关性质”时，教师可以利用“如何求圆的周长”的问题进行导入，引导学生探究圆的周长公式，进而引出圆周率。在讲解“点和圆、直线和圆的位置关系”时，教师可以通过游戏探索的方式，让学生通过动手操作理解点和圆的位置关系、直线和圆的位置关系。

（二）布置学习任务，深度探索知识

在大单元教学中，教师需要布置具有挑战性的学习任务，如实验探究、项目学习人物等，引导学生对单元知识内容进行深度加工，开展多维实践、探索，助力学生逐步从低阶思维转变为高阶思维。

在深度探索环节，教师可以实验探究、项目学习任务为切入点，引导学生对单元知识内容进行深度加工，走进更绚丽多彩的数学世界。例如，在讲解“点和圆、直线和圆的位置关系”时，教师可以设计以下实验活动：1.给学生提供大头针和圆形纸板，让学生自己动手确定点和圆的位置关系［4］。2.引导学生通过测量和计算来确定直线和圆的位置关系。教师可以让学生将大头针插入纸板中，观察大头针和圆之间的关系，引导学生思考：“当大头针在圆内、圆上或圆外时，它们之间的位置关系如何？”教师还可以给学生提供直尺和圆形纸板，要求学生用量角器和直尺测量当直线和圆相交、相切或相离时，直线和圆之间的角度和距离关系。

又如，在讲解“正多边形和圆”时，教师可以设计剪正多边形图案的项目任务。项目实施步骤如下：1.明确自己想剪的正多边形的边数、大小和形状等。2.挑选合适的圆规、直尺、量角器等工具，并根据正多边形的特点和要求设计相应的制作步骤。3.通过合作、互动、实践等，完成剪正多边形图案的任务。这个过程能够使学生更深入地理解正多边形和圆的关系及相关的几何知识。

三、铺设“迁移之桥”，建构大单元知识结构

（一）搭建知识之间的桥梁，帮助学生构建知识网络

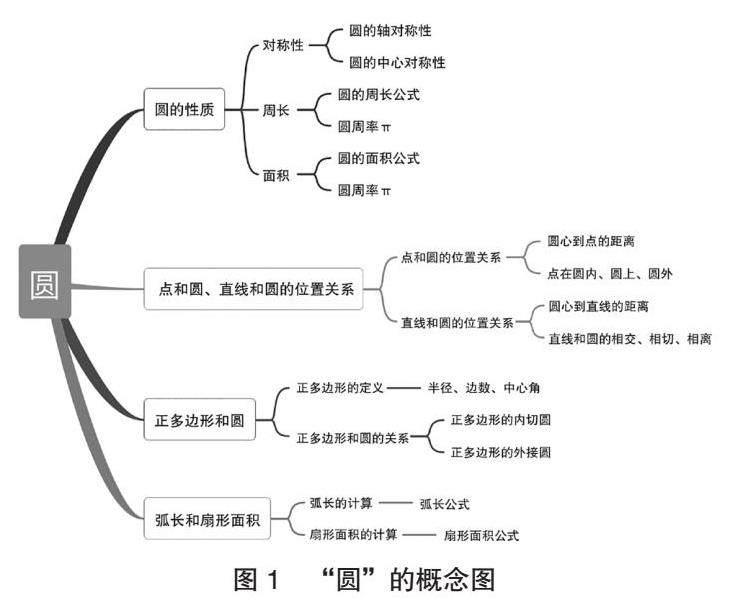
在大单元教学中，教师需要关注知识之间的内在联系，并通过有效的教学手段，帮助学生搭建知识之间的桥梁。具体而言，教师可以利用思维导图、概念图等，直观地展示知识之间的联系，帮助学生构建系统的知识网络，引导学生发现知识之间的相似性，从而实现知识的迁移［5］。

教师可以将“圆”这一章的知识点以概念图的形式呈现（如图1所示），帮助学生理解和掌握知识点之间的联系。接着，教师可以引导学生发掘知识间的共性，如圆的部分性质和直线、三角形等其他几何图形的性质相似。教师可以引导学生进行类比学习，通过对比发现知识之间的相同和不同之处，加深学生对圆的理解和记忆。

（二）关注数学思想方法的迁移，提高学生的思维品质

数学思想方法是数学学习的精髓，可以帮助学生更好地理解和应用数学知识。在大单元教学中，教师应该有意识、有针对性地揭示所学内容中蕴含的数学思想方法，如分类讨论、数形结合、化归思想等，并通过具体的例子，引导学生理解和掌握数学思想方法。同时，教师要鼓励学生将这些思想方法迁移到解决其他数学问题的过程中，循序渐进地提高学生的数学思维品质。

在这一章的教学中，教师可以从不同角度阐述分类讨论、数形结合、转化思想等数学思想方法，揭示数学内容中的深刻原理。例如，在探究直线和圆的位置关系时，教师可以引导学生根据圆心到直线的距离与圆的半径之间的关系，分类讨论圆与直线相离、相切、相交三种情况的特点，并用符号语言表示它们之间的关系，让学生掌握分类讨论思想。又如，在探究圆的对称性时，教师可以引导学生借助圆的示意图，发现圆绕它的圆心旋转任意角度后都能与自身重合；在探究圆的周长和面积时，教师可以让学生利用圆规来测量圆的周长和面积，从而发现圆的周长与直径之间的关系，以及圆的面积与半径之间的关系。这样能让学生掌握数形结合思想。再如，在探究弧长和扇形面积时，教师可以引导学生利用化归思想，将弧长和扇形面积的计算转化为线段和扇形的计算。

四、奏响“评价之歌”，提高大单元教学质量

评价是促进学生深度学习，提高大单元教学质量的重要保障。教师作为教学评价的核心人物，可以从评价指标、评价主体、评价方法等多个维度着手，构建评价体系。首先，评价指标多元化。评价指标应围绕大单元教学的目标进行设计，关注学生在学习过程中的认知、技能和情感等方面的发展。教师可以设置概念理解、问题解决、探究能力、合作精神、创新思维等评价指标。其次，评价主体多元化。评价主体应包括教师、学生等。教师应让学生参与评价过程，开展学生自评、学生互评。在学生完成评价后，教师需要对学生的学习情况进行综合评价。最后，评价方法多元化。教师应采用具有多样性和灵活性的评价方法，将形成性评价、总结性评价和表现性评价相

结合，从而更全面地了解学生的学习情况，提高教学效果。

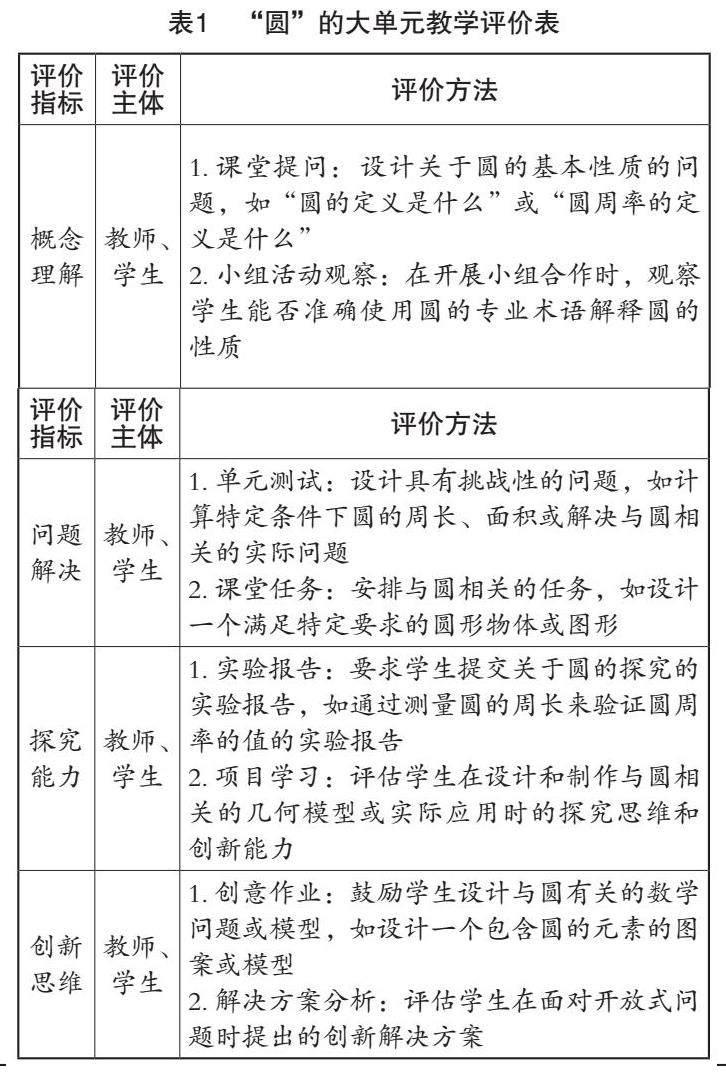
在这一章的大单元教学中，教师可以从评价指标、评价主体、评价方法等维度着手，构建大单元教学评价新体系（如表1所示）。

结语

文章以人教版数学九年级上册第二十四章“圆”的教学为例，从设计问题链、开展探究活动、迁移所学知识、构建评价体系等多个维度，详细探讨了深度学习视角下开展初中数学大单元教学的实践策略。通过实施这些策略，教师可以有效开展初中数学大单元教学，引导学生开展深度学习，真正提高学生的数学核心素养。未来，教师应进一步深化大单元教学实践，培养学生的核心素养。

【参考文献】

［1］朱宏.以核心素养为导向的初中数学大单元教学探究［J］.教学管理与教育研究，2023，8（22）：88-90.

［2］黄秋燕.基于大单元教学的初中数学整体教学实践［J］.数理化解题研究，2023（32）：32-34.

［3］詹雅木.立足大单元有效实施复习：大单元教学视域下初中数学单元复习课教学设计的探究［J］.考试周刊，2023（46）：66-71.

［4］王文明.新课改背景下初中数学大单元教学的实践探索［J］.数理天地（初中版），2023（21）：71-73.

［5］吴岚.基于核心素养的初中数学大单元教学设计与实践［J］.天津教育，2023（33）：10-12.