基于鲸鱼优化算法支持向量回归的汽车运动状态估计

尤勇 孟云龙 吴景涛 王长青

摘要：

为了不依赖动力学模型精度而准确地获取车辆运动状态信息，提出一种基于鲸鱼优化算法支持向量回归（WOA-SVR）的车辆状态估计算法。首先通过分析车辆动力学基本特性，设计了侧向速度、横摆角速度与车速分离的支持向量回归估计架构；然后对支持向量回归（SVR）模型进行多种行驶工况组成的数据集训练，在训练过程中运用鲸鱼优化算法对松弛变量中的惩罚因子c与核函数参数g进行寻优；最后对估计算法进行单移线、扫频试验虚拟仿真和实车ABS制动、双移线试验验证。结果表明，该算法有效提高了估计精度，且对车速的变化具有鲁棒性，可以实现准确的不依赖动力学模型精度的汽车运动状态估计。

关键词：车辆状态估计；动力学模型；机器学习；支持向量回归；鲸鱼优化算法

中图分类号：U461.1

DOI：10.3969/j.issn.1004132X.2024.06.003

开放科学（资源服务）标识码（OSID）：

Vehicle Motion State Estimation Based on WOA-SVR

YOU Yong1，2  MENG Yunlong1，2  WU Jingtao1，2  WANG Changqing3

1.College of Mechanical Engineering，Hebei University of Technology，Tianjin，300400

2.Tianjin Key Laboratory of Power Transmission and Safety Technology for New Energy Vehicles，

Tianjin，300131

3.CATARC Automotive Test Center（Tianjin） Co.，Ltd.，Tianjin，300300

Abstract： In order to accurately obtain vehicle motion state information without relying on the accuracy of the dynamics model， a vehicle state estimation algorithm was proposed based on WOA-SVR. Firstly， by analyzing the basic characteristics of vehicle dynamics， a SVR architecture was designed for estimating the separation of lateral velocity， yaw rate， and vehicle speed. Then， the SVR model was trained on a dataset composed of multiple driving conditions， and the WOA was used to optimize the penalty factor c and kernel function parameter g in the relaxation variables during the training processes. Finally， the estimation algorithm was validated through virtual simulation of single line shift and frequency sweep tests， as well as ABS braking and double line shift actual vehicle tests. The results show that this algorithm effectively improves estimation accuracy and is robust to changes in speed， enabling accurate estimation of vehicle motion states without relying on dynamics models.

Key words： vehicle state estimation； dynamics model； machine learning； support vector regression（SVR）； whale optimization algorithm（WOA）

收稿日期：20231008

基金项目：天津市教委科研项目（2023KJ298）；国家自然科学基金（52205052）

0  引言

随着汽车向电动化与智能化发展，汽车主动控制系统与智能驾驶辅助系统逐渐被采用。主动控制、驾驶辅助系统的实现均是以获取汽车基本运动状态为基础的，但由于受传感器精度、成本等问题限制，有些车辆状态参数无法直接用传感器进行测量，如纵向速度、侧向速度和横摆角速度等，合理的办法是利用低成本的传感器得到易获取的状态信息，如纵向加速度、侧向加速度、轮速等，再通过估计算法得到所需参数［1-2］，因此如何准确并快速地获取汽车行驶状态参数成为研究的热点［3-6］。

目前，汽车状态估计算法有传统的卡尔曼滤波（Kalman filter，KF）算法及其改进算法，融合估计算法、基于机器学习的回归算法以及其他相关估计算法等。

扩展卡尔曼滤波（extended Kalman filter，EKF）算法和无迹卡尔曼滤波（unscented Kalman filter，UKF）算法是常用的卡尔曼滤波（KF）改进算法［7-11］。为了提高估计精度，一些研究者将KF改进算法与其他算法作了融合［12-15］。如文献［12］将EKF与模糊算法结合，实现了EKF估计自适应调节，提高了行驶状态估计的准确性和鲁棒性；文献［13］与文献［14］分别将遗传算法和自适应神经模糊推理系统（adaptive network-based fuzzy inference system，ANFIS）融合进行汽车状态估计；文献［15］基于建立的三自由度车辆动力学模型提出EKF的分级串联状态估计，并进行了联合仿真验证。大多数基于KF的估计算法有较高的估计精度，但它们受限于整车运动学模型，需要精准的模型参数才能求解，因此基于KF的算法具有一定的局限性。

为了解决依赖运动学模型的问题，一些研究者将机器学习算法运用到车辆状态估计上。基于机器学习的回归算法不依赖汽车运动学模型精度和车辆固有参数，通过模型结构和训练数据集来估计车辆状态参数。文献［16］提出了粒子群优化神经网络的机器学习回归算法，通过低成本传感器获取易测量的参数来进行模型训练并估计出所需的变量；文献［17］设计了适合于车辆运动状态估计的混合神经网络（hybrid neural network，HNN）架构，此方法对路面附着系数变化具有鲁棒性，实现了车辆运动状态的深度学习估计；文献［18］使用多层长短期记忆网络（long short-term memory，LSTM）估计质心侧偏角；文献［19］使用人工神经网络构建了质心侧偏角的估计算法，并通过CarSim仿真软件验证了估计性能。目前，支持向量回归（support vector regression，SVR）应用在汽车行驶状态估计方面的研究较少，但SVR算法已经在其他领域得到应用，并取得了较好的估计效果［20-21］。

基于鲸鱼优化算法支持向量回归的汽车运动状态估计——尤  勇  孟云龙  吴景涛等

中国机械工程 第35卷 第6期 2024年6月

本文提出了一种基于鲸鱼优化算法（whale optimization algorithm，WOA）支持向量回归（SVR）的车辆运动状态估计算法。通过分析车辆本身的动力学基本特性，设计了SVR算法结构，实现了车辆运动状态的机器学习估计；然后运用CarSim/Simulink软件对多种工况数据进行采集，并对SVR模型进行训练；在模型训练过程中运用鲸鱼优化算法（WOA）对SVR松弛变量中的惩罚因子c与核函数参数g进行寻优；最后通过MATLAB仿真和实车试验验证了采用WOA-SVR算法估计车辆状态的可行性。

1  WOA-SVR工作原理

1.1  支持向量回归

支持向量回归算法是一种监督学习算法，用于预测离散值。它是支持向量机（support vector machine，SVM）对回归问题的一种应用［20-21］。支持向量机是对数据进行二元分类的广义线性分类器。如图1所示，在一个二维平面内分布有m个圆点，则给定数据集T为

T={（x（1），y（1）），（x（2），y（2）），…，（x（m），y（m），）}（1）

将数据集T中的样本点拟合到超平面h（x（i））中，表达式为h（x（i））=φ（x（i））θ（i）+b。其中，φ（x（i））为平面上的数据点，θ为模型参数向量，θ=（θ（1），θ（2），…，θ（i）），b为偏置量。将离超平面最远的一些样本点称为支持向量，计算支持向量到超平面h（x（i））的几何间隔d：

d=y（i）（φ（x（i））θ（i）+b）1‖θ‖（2）

SVR问题的求解要点就是求间隔d集合的最大值，从而最终求得有最大间隔dmax的超平面。求d的最大值问题可转化为求‖θ‖最小值的问题，即可以转化为二次规划问题。假设共有n个支持向量，加入松弛变量使间隔最大化，则目标函数变为

minθ，b，ξup，ξdown12‖θ‖22+c∑ni=1（ξupi+ξdowni）（3）

s.t. y（i）－φ（x（i））θ（i）－b≤ξupi+ε

φ（x（i））θ（i）+b－y（i）≤ξdowni+ε

ξupi≥0  ξdowni≥0

式中，ξup、ξdown为松弛变量的上下限向量，ξup=（ξup1，ξup2，…，ξupm），ξdown=（ξdown1，ξdown2，…，ξdownm）；c为惩罚系数；ε为容忍损失。

惩罚系数c（c＞0）用来控制间隔和松弛变量惩罚的平衡。将二次规划问题转化为凸优化问题，构造拉格朗日函数如下：

L（θ（i），b，ξupi，ξdowni，λupi，λdowni，μupi，μdowni）=

c∑ni=1（ξupi+ξdowni）+∑ni=1μupiξupi－∑ni=1μdowniξdowni+

12‖θ‖22+∑ni=1λupi（y（i）－φ（x（i））θ（i）－b－ξupi－ε）+

∑ni=1λdowni（φ（x（i））θ（i）+b－y（i）－ξdowni－ε）（4）

式中，λupi、λdowni、μupi、μdowni为拉格朗日变量。

将优化问题转化为等价的对偶问题，对参数θ（i），b，ξupi，ξdowni求偏导，并令各偏导式为0，解方程得到各参数结果后代入到式（4）中，可得

L（θ（i），b，ξupi，ξdowni，λupi，λdowni，μupi，μdowni）=

12θTθ+c∑ni=1ξupi－

∑ni=1μupiξupi－∑ni=1λupiφ（x（i））θ（i）－

∑ni=1λupib+∑ni=1λupiy（i）－∑ni=1λupiξupi－∑ni=1λupiε+

c∑ni=1ξdowni－∑ni=1μdowniξdowni+∑ni=1λdowniφ（x（i））θ（i）+

∑ni=1λdownib－∑ni=1λdowniy（i）－∑ni=1λdowniξdowni－∑ni=1λdowniε=

∑ni=1y（i）（λupi－λdowni）－ε∑ni=1（λupi+λdowni）－

12［∑ni=1（λupi－λdowni）φ（x）］［∑nj=1（λupj－λdownj）（φ（x））T］=

∑ni=1［y（i）（λupi－λdowni）－ε（λupi+λdowni）］－

12∑ni=1∑nj=1（λupi－λdowni）（λupj－λdownj）φ（x）（φ（x））T（5）

求出式（5）极小化对应的ξupi、ξdowni的值，便可推导出模型参数θ对应的最优值：

θ*=∑ni=1（λupi－λdowni）（φ（x））T（6）

SVR的KKT（Karush-Kuhn-Tucker）条件为

0≤λupi  λdowni≤c  λupiλdowni=0

λupi（y（i）－φ（x（i））θ（i）－b－ξupi－ε）=0

λdowni（φ（x（i））θ（i）+b－y（i）－ξdowni－ε）=0

y（i）－φ（x（i））θ（i）－b－ξupi－ε≤0

φ（x（i））θ（i）+b－y（i）－ξdowni－ε≤0

（c－λdowni）ξdowni=0  （c－λdowni）ξdowni=0

ξupiξdowni=0  ξupi≥0  ξdowni≥0（7）

根据SVR的KKT条件，对于［x（i），y（i）］，都有（c-λupi）ξupi=0，在得到λupi后，如果0＜λupi＜c，则一定有λdowni=0，ξupi=0。λupi可以取（0，c）的任意值，即可以通过b（i）=y（i）-φ（x（i））θ（i）-ε求取多个b（i）值，用多个b（i）的平均值作为最后结果：

b*=1n∑ni=1b（i）（8）

将θ*与b*代入到超平面表达式中，最终求得SVR超平面为

y^（i）=φ（x（i））θ*（i）+b*=

∑ni=1（λupi－λdowni）φ（x）（φ（x））T－1n∑ni=1（y（i）+ε）－

1n∑ni=1［∑nj=1（λupi，j－λdowni，j）］φ（x）（φ（x））T（9）

1.2  核函数的选取

当数据集在原始特征中不是线性可分时，在支持向量机中引入核函数Φ（·），通过核函数将原始特征空间映射为更高维的空间，将原始空间中不可分的数据在高维空间中变成线性可分，此时再在高维空间进行数据集分类。核函数是用来解决映射后高维空间中样本距离‖Φ（xi）-Φ（xj）‖计算的，通常表示为

‖Φ（xi）－Φ（xj）‖2=

k（xi，xi）－2k（xi，xj）+k（xj，xj）（10）

选用常用的高斯核函数为

k（xi，xj）=exp（－‖xi－xj‖22g2）（11）

式中，g为核函数参数。

1.3  WOA优化算法

SVR中惩罚因子c与核函数参数g都将影响估计的效果。惩罚因子c影响算法的容忍程度，c越大越能容忍出现误差，但这样容易欠拟合；c越小则越容易出现过拟合。核函数参数g决定了数据映射到新的特征空间后的分布，g越大支持向量越少。c、g过大或过小都影响估计的速度与精度。本文中运用鲸鱼优化算法（WOA）对c和g进行优化。

WOA是根据鲸鱼围捕猎物的行为而提出的算法，采用随机或最佳搜索代理来模拟捕猎行为。WOA算法机制简单、参数少、寻优能力强［22］。算法流程如图2所示。

WOA算法中个体之间距离与位置向量分别为

D=CX*（t）－X（t）

X（t+1）=X*（t）－AD（12）

其中，t为当前迭代次数；D为当前鲸鱼与随机鲸鱼之间的距离向量；X（t）为位置向量；X *（t）为目前得到的最佳解的位置向量；A、C为系数，A=2a（t）r1（t），C=2r2（t）。在整个迭代过程中收敛因子a由2线性降到0；r1、r2为［0，1］中的随机向量。

WOA算法中鲸鱼捕食主要有两个机制：包围捕食和气泡网捕食。因此根据概率P来选择气泡网捕食或者收缩包围，位置更新公式如下：

X（t+1）=X（t）－AD          P≤0.5

D′exp（BL）cos（2πL）+X（t）P＞0.5（13）

式中，D′为当前搜索个体与当前最优解的距离向量；B为螺旋形状参数；L为在［-1，1］均匀分布的随机数；P为捕食机制概率，值域为［0，1］的随机数。

随着迭代次数t的增加，参数A和收敛因子a逐渐减小，若|A|<1，则鲸群逐渐包围当前最优解，处于局部寻优阶段。为保证所有鲸鱼都能在解空间中充分搜索，WOA根据鲸鱼彼此间的距离来更新位置，达到随机搜索的目的。因此，当|A| ≥ 1时，搜索个体会游向随机鲸，从而得到最优解：

D″=CXrand（t）－X（t）

X（t+1）=Xrand（t）－AD（14）

式中，D″为当前搜索个体与随机个体的距离向量；Xrand（t）为当前随机个体的位置。

以SVR训练结果的均方根误差（RMSE）最小值作为目标函数：

XRMSE=∑Nk=1（Xo，k－Xm，k）2N（15）

式中，XRMSE为均方值误差值；N为估计次数；Xo，k为真实值；Xm，k为估计值。

惩罚因子c与核函数参数g的优化范围分别为［10-2，103］与［2-5，28］。WOA参数设置如表1所示。

2  车辆状态估计算法设计

2.1  三自由度车辆模型

为了对纵向速度、侧向速度和横摆角速度这

三个变量进行估计，在二自由度车体模型的基础上引入纵向速度建立三自由度车辆模型［1］，如图3所示。

车辆状态方程为

γ·=a2cCf+b2cCrIzvx+（acCf－bcCr）β－acCfδIz

β·=acCfγ－bcCrγMv2x－γ+（Cf+Cr）β－CfδMvx

v·x=vxβγ+ax（16）

式中，γ为横摆角速度；β为质心侧偏角；ac、bc分别为质心到前后轴距离；Iz为绕z轴转动惯量；vx为纵向车速；δ为前轮转角；M为汽车质量；ax为纵向加速度；ay为侧向加速度；Cf、Cr分别为前后轮侧偏刚度。

车辆建模忽略了车辆悬架系统的影响，只考虑车辆三个方向的自由度，包括沿x轴的前向速度vx，沿y轴的侧向运动vy与绕z轴的横摆运动γ，由于β=vy/vx，故沿y轴的侧向运动可由β代替。将EKF算法作为对比验证算法，将式（16）作为状态方程，则观测方程为

ay=acCf－bcCrMvxγ+Cf+CrMβ－CfMδ（17）

2.2  车辆状态估计结构

从车辆状态方程可以看出，侧向速度与横摆角速度取决于前轮转角和纵向速度。纵向速度为控制输入，而非状态变量，纵向速度主要取决于轮速，它们之间为非线性耦合关系，不具有显式的时序依赖［16］，所以应将纵向速度单独进行估计，再利用估计出来的车速进行侧向速度与横摆角速度估计，在训练SVR模型时也应进行单独的训练。

本文设计了图4所示的SVR估计双层结构：纵向估计层与侧向估计层。考虑成本与精度问题，目前传感器较容易测得的车辆状态参数有轮速以及纵横向加速度等。纵向估计层以四个车轮轮速与纵向加速度为输入，以车速为输出。侧向估计层以车速、纵向加速度和侧向加速度为输入，以侧向速度和横摆角速度为输出。

2.3  训练数据采集

在前期工作中通过参数调整进行某款电动汽车CarSim建模，与实际整车性能进行匹配。然后选择多种常见仿真工况，通过CarSim与Simulink联合仿真采集车辆动态响应数据，从而构建多种工况数据集，采集数据过程如图5所示。

数据采集工况包含纵向和侧向两个部分。纵向工况包括加速工况和制动工况。加速工况纵向加速度分别为0.1g、0.2g、0.3g；制动工况为50～100 km/h下全力制动，间隔为10 km/h。侧向工况包括双移线工况、正弦转向输入工况以及稳态回转工况。双移线与正弦转向工况下车速在50～100 km/h范围内变化，间隔为10 km/h；稳态回转工况侧向加速度应达到0.7g，如表2所示。其中纵向参数训练集包括四个车轮的轮速、车速以及质心的纵向加速度，共计19 608个样本；侧向参数训练集包括车速、侧向速度以及质心的纵向加速度、侧向加速度和横摆角速度，共计28 639个样本。

2.4  数据处理与模型训练

数据处理与模型训练的过程如图6所示。采用10 Hz低通滤波方式对车辆信息有较好的滤波效果，能有效地分离有用数据和噪声，提高分析精度。然后对滤波后的数据进行归一化处理，可以有效缩短回归拟合的时间，提高估计准确率；运用

WOA算法对SVR松弛变量中的惩罚因子c与核函数参数g进行寻优，得到最佳参数，然后采用独立训练的方式获得最佳的SVR估计模型。

纵向训练模型输入参数为轮速与纵向加速度，输出参数为车速；侧向训练模型输入参数为车速、侧向加速度与纵向加速度，输出参数为侧向速度以及横摆角速度。

3  仿真结果验证

试验测试工况为扫频工况和单移线工况，扫频工况验证WOA-SVR算法在高频、小侧向加速度工况下的估计效果，单移线工况验证WOA-SVR算法在瞬态、大侧向加速度工况下的估计效果。扫频工况输入频率由0.1 Hz增加到0.5 Hz，幅值从40°降低到5°，车速为100 km/h，图7为扫频工况转向盘转角曲线；单移线工况车速为100 km/h，单移线路径如图8所示，驾驶员预瞄时间为0.5 s。

扫频工况与单移线工况模型输入参数为轮速、纵向加速度与侧向加速度，输出参数为车速、侧向速度与横摆角速度。在CarSim软件中运行上述两种测试工况，在MATLAB/ Simulink中编写状态估计程序，并与EKF估计值进行对比，得到图9、图10所示的估计结果。两种算法估计误差值对比如表3所示，其中，MAE为平均绝对值误差，RMSE为均方根误差。

如图9所示，在扫频工况中，与WOA-SVR算法相比，EKF算法对车速的估计误差较大，以及在转向盘转角较大时对侧向速度和横摆角速度估计误差较大。如图10所示，在单移线工况中， EKF算法在车辆进行单移线动作时对车速、侧向速度和横摆角速度估计误差较大。结合表3所示估计误差，WOA-SVR算法在仿真验证工况下相较于传统的EKF算法具有明显优势。

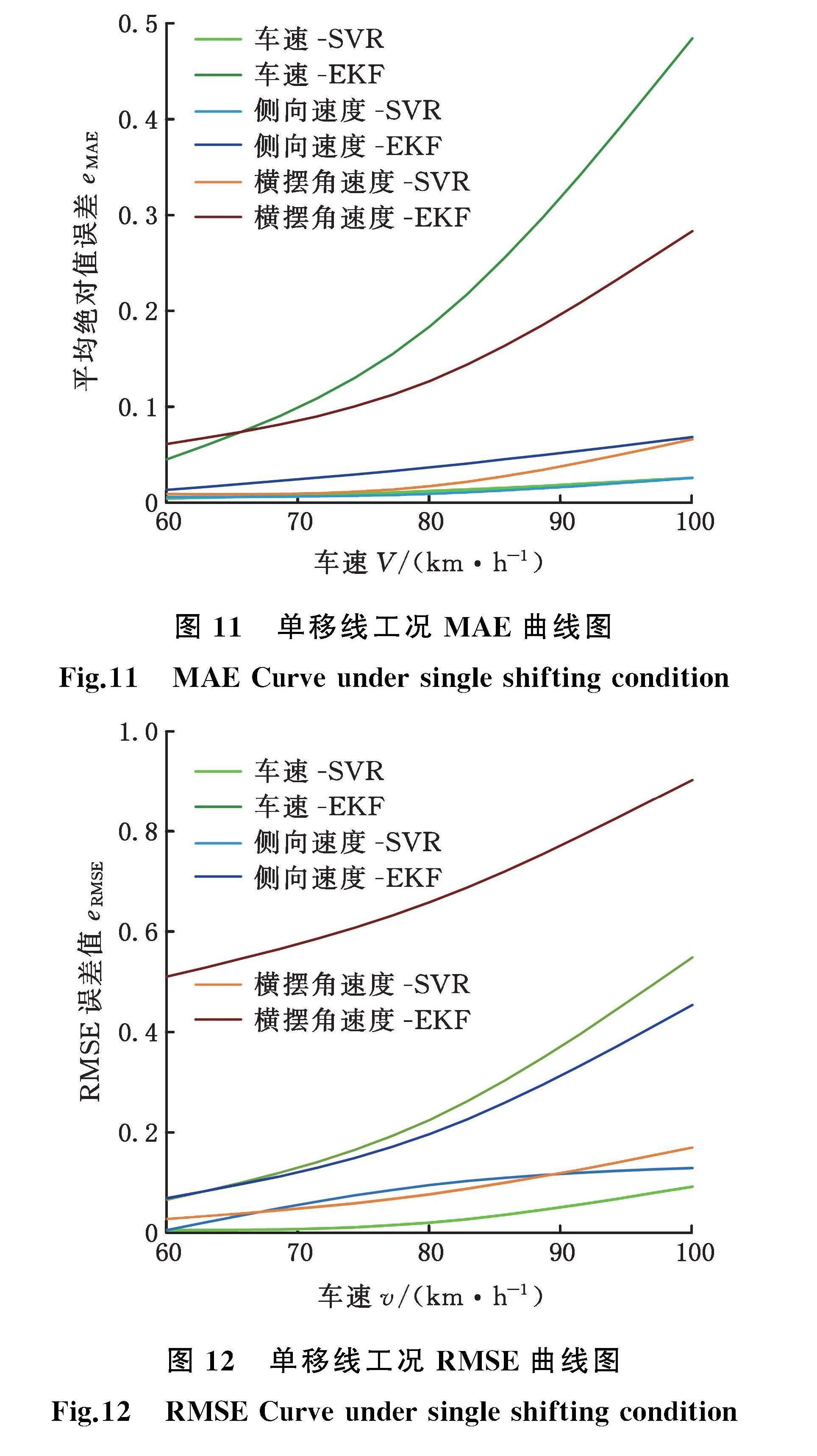
为进一步研究车速对估计误差的影响，分别以60，70，80， 90，100 km/h的车速进行单移线仿真试验，并将得到的MAE和RMSE误差值与车速的关系曲线进行线性拟合，得到图11、图12所示的结果。如图11、图12所示，传统的EKF算法随着车速的增大，车速和横摆角速度的MAE值以及所有估计参数的RMSE值会显著提高， OA-SVR算法在车速增大时MAE值与RMSE值增大并不明显，可以说明本文提出的WOA-SVR算法对车速的增大具有鲁棒性，在不同车速工况下仍可以保持较小的估计误差。

4  实车试验验证

为进一步验证所提出算法的可行性，在某试验场地进行实车试验。实车试验共包含两部分：ABS制动试验（GB 21670—2008）与80 km/h双移线试验（ISO 3888-1）。在汽车进行紧急制动时，会出现ABS系统介入使汽车轮速不接近于车速的情况，此时依据轮速对车速进行估计会有一定的困难。ABS制动试验是为了验证面对复杂、紧急的制动工况下保证纵向状态参数（车速）估计的准确性。双移线试验是为了验证侧向状态参数（侧向速度、横摆角速度）估计的准确性。

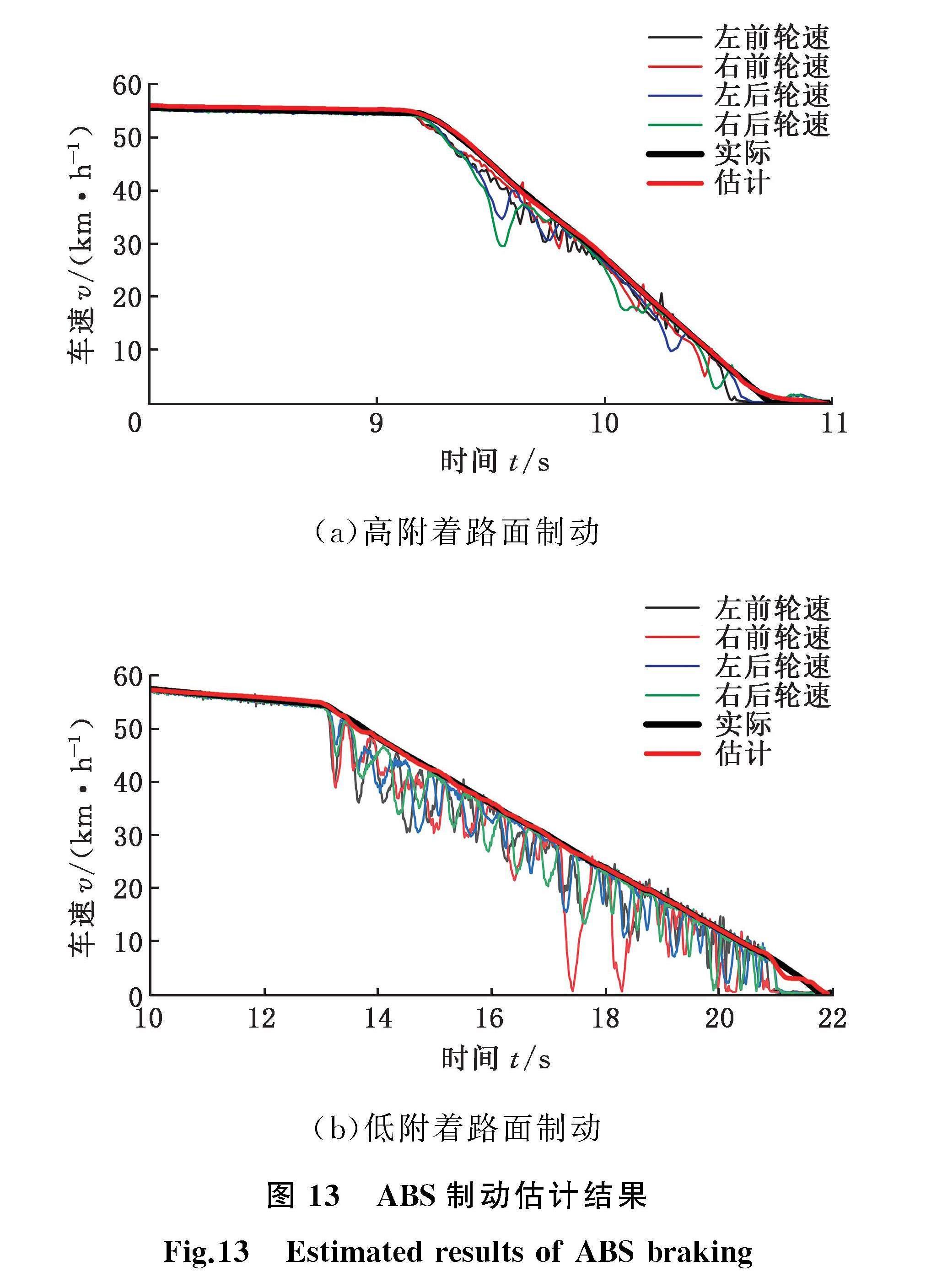
ABS制动试验即在高附着路面和低附着路面从55 km/h的初速度下制动，并触发ABS功能。通过采集车辆的CAN信号，获得车辆轮速、车速和纵向加速度等试验数据。双移线试验时在试验车辆上安装陀螺仪、数据采集装置等试验设备，采集车速、侧向速度、纵向加速度、侧向加速度和横摆角速度等试验数据。

ABS制动试验中根据四个车轮的轮速和纵向加速度估计车速，并与实际车速进行对比，结果如图13所示。80 km/h车速下的双移线试验中根据车速、纵向与侧向加速度估计侧向速度与横摆角速度，结果如图14所示。

ABS制动试验和双移线试验的估计误差值如表4所示。

由图13、图14与表4可知，估计结果与实车结果的误差较小，进一步说明WOA-SVR算法可以在实车复杂的工况与环境下准确地对车辆的纵向和侧向运动状态参数进行估计。

5  结论

本文提出了一种不依靠车辆动力学模型和车辆参数精度的基于鲸鱼优化支持向量回归（WOA-SVR）的运动状态估计算法。

首先，对车辆动力学特性进行分析，将车速估计与侧向速度、横摆角速度估计分离，构成两层SVR估计结构。

然后运用CarSim对多种工况数据进行采集，利用采集到的数据对两侧估计结构分别进行SVR模型训练，在训练过程中运用WOA算法对SVR算法中的惩罚因子c与核函数参数g进行寻优，得到最佳算法参数。

最后在MATLAB/Simlink仿真和实车试验中验证WOA-SVR算法的可行性。仿真验证中选择单移线与扫频工况，实车试验中选择制动与双移线工况。验证结果表明，WOA-SVR算法具有良好的估计精度，且对车速的变化具有鲁棒性，可以实现准确的不依靠动力学模型的汽车运动状态估计。

参考文献：

［1］  李亮.汽车动力学与控制［M］.北京：清华大学出版社，2022：130-147.

LI Liang.Vehicle Dynamics and Control［M］.Beijing：Tsinghua University Press，2022：130-147.

［2］  GUO Hongyan，CAO Dongpu，CHEN Hong，et al. Vehicle Dynamic State Estimation：State of the Art Schemes and Perspectives［J］. IEEE/CAA Journal of Automatica Sinica，2018，5（2）：418-431.

［3］  PENDLETON S D，ANDERSEN H，DU X X，et al. Perception，Planning，Control，and Coordination for Autonomous Vehicles［J］. Machines，2017，5（1）：54.

［4］  章仁燮， 熊璐， 余卓平. 智能汽车转向轮转角主动控制［J］.机械工程学报， 2017， 53（14）：106-113.

ZHANG Renxie， XIONG Lu， YU Zhuoping. Active Control of Steering Wheel Angle of Smart Car［J］.Journal of Mechanical Engineering， 2017， 53（14）：106-113.

［5］  KUUTTI S，BOWDEN R，JIN Y，et al. A Survey of Deep Learning Applications to Autonomous Vehicle Control［J］. IEEE Transactions on ITS，2021，22（2）：712-733.

［6］  ZHA Y，QUAN X，MA F，et al. Stability Control for a Fourwheel-independent-drive Electric Vehicle Based on Model Predictive Control［J］. SAE International Journal of Vehicle Dynamics，Stability，and NVH，2021，5（2）：191-204.

［7］  李旭，宋翔，张为公.基于扩展卡尔曼滤波的车辆状态可靠估计［J］.东南大学学报（自然科学版），2014，44（4）：740-744.

LI Xu， SONG Xiang， ZHANG Weigong. Reliable Vehicle State Estimation Based on Improved Extended Kalman Filter［J］. Journal of Southeast University（Natural Science Edition）， 2014，44（4）：740-744.

［8］  宗长富，潘钊，胡丹，等.基于扩展卡尔曼滤波的信息融合技术在车辆状态估计中的应用［J］.机械工程学报，2009，45（10）：272-277.

ZONG Changfu， PAN Zhao， HU Dan，et al. Information Fusion Algorithm for Vehicle State Estimation Based on Extended Kalman Filtering［J］. Journal of Mechanical Engineering，2009，45（10）：272-277.

［9］  KATRINIOK A，ABEL D. Adaptive EKF-based Vehicle State Estimation with Online Assessment of Local Observability［J］. IEEE Transactions on Control Systems Technology，2016，24（4）：1368-1381.

［10］  芦冰，解小华，蔡可天，等.UKF车速估计器的算法研究与仿真［J］.吉林大学学报（信息科学版），2015，33（1）：7-11.

LU Bing， XIE Xiaohua， CAI Ketian，et al. Speed Estimation Research and Simulation Based on UKF Algorithm［J］.Journal of Jilin University（Information Science Edition），2015，33（1） ：7-11.

［11］  李行健.四轮独立驱动电动汽车状态估计算法研究［D］. 重庆：重庆大学，2018.

LI Xingjian. Study on State Estimation Algorithm for Four-wheel-independent-drive Electric Vehicles［D］. Chongqing ：Chongqing University，2018.

［12］  刘明春，彭志波，吴晓建.基于自适应模糊扩展卡尔曼滤波的车辆运动状态联合估计［J］.汽车技术，2022， 559（4）：23-30.

LIU Mingchun， PENG Zhibo， WU Xiaojian. Joint Estimation of Vehicle Motion State Based on Adaptive Fuzzy Extended Kalman Filter［J］.Automobile Technology， 2022， 559（4）：23-30.

［13］  周卫琪，齐翔，陈龙，等. 基于无迹卡尔曼滤波与遗传算法相结合的车辆状态估计［J］. 汽车工程，2019，41（2）：198-205.

ZHOU Weiqi，QI Xiang，CHEN Long，et al. Vehicle State Estimation Based on the Combination of Unscented Kalman Filtering and Genetic Algorithm［J］. Automotive Engineering， 2019， 41（2）：198-205.

［14］  BOADA B L， BOADA M J L， DIAZ V. Vehicle Sideslip Angle Measurement Based on Sensor Data Fusion Using an Integrated ANFIS and an Unscented Kalman Filter Algorithm［J］. Mechanical Systems and Signal Processing， 2016， 72：832-845.

［15］  陈龙，刘巧斌，陶磊.基于GS-EKF滤波方法的车辆状态参数估计［J］.东北大学学报（自然科学版），2023，44（8）：1144-1151.

CHEN Long， LIU Qiaobin， TAO Lei. Vehicle State Parameter Estimation Based on Graded Series Extended Kalman Filter Method［J］. Journal of Northeastern University（ Natural Science）， 2023， 44（8）：1144-1151.

［16］  LIU Y J， SUN Q Y， CUI D W. Vehicle State Estimation Based on PSO-RBF Neural Network［J］. International Journal of Vehicle Safety， 2019， 11（1）：93-106.

［17］  高振海，温文昊，唐明弘，等.基于混合神经网络的汽车运动状态估计［J］.汽车工程，2022，44（10）：1527-1536.

GAO Zhenhai， WEN Wenhao， TANG Minghong，et al. Estimation of Vehicle Motion State Based on Hybrid Neural Network［J］. Automotive Engineering，2022，44（10）：1527-1536.

［18］  TONOLI A， AMATI N， GHOSH J. A Deep Learning Based Virtual Sensor for Vehicle Sideslip Angle Estimation：Experimental Results［J］.SAE Paper， 2018- 01-1089.

［19］  CHINDAMO D， GADOLA M. Estimation of Vehicle Side-slip Angle Using an Artificial Neural Network［C］∥2nd International Conference on Mechanical， Aeronautical and Automotive Engineering（ICMAA 2018）. Online， 2018 ：201816602001.

［20］  梁杨，周永军，蒋淑霞，等.基于改进GWO-SVR的锂电池SOH估计［J］.电子测量技术，2023，46（7）：13-18.

LIANG Yang， ZHOU Yongjun， JIANG Shuxia，et al.Lithium Battery SOH Estimation Based on Improved GWO-SVR［J］. Electronic Measurement Technology， 2023，46（7）：13-18.

［21］  何彦，肖圳，李育锋，等.使用CNN-SVR的汽车组合仪表组装质量预测方法［J］.中国机械工程，2022，33（7）：825-833.

HE Yan， XIAO Zhen， LI Yufeng，et al. An Assembly Quality Prediction Method for Automotive Instrument Clusters Using CNN-SVR［J］.China Mechanical Engineering， 2022， 33（7）：825-833

［22］  许傲然，戴菁，谷彩莲，等.基于WOA优化扩展卡尔曼算法的锂离子电池SOC估算研究［J/OL］.电源学报：1-11［2023-10-08］. http：∥kns.cnki.net/kcms/ detail/ 12.1420.TM.20220826.1321.005.html.

XU Aoran， DAI Jing， GU Cailian，et al. Research on SOC Estimation of Lithiumion Battery Based on WOA Optimization Extended Kalman Algorithm［J/OL］. Journal of Power Supply：1-11［2023-10-08］. http：∥kns.cnki.net/kcms/detail/12.1420.TM. 20220826.1321.005.html.

（编辑  王艳丽）

作者简介：

尤  勇，男，1989年生，讲师、博士。研究方向为车辆动力传动及综合控制、新能源汽车底盘智能控制及能量管理。E-mail：yongyou@hebut.edu.cn。