数形结合在高中数学解题中的应用

邓军民

我国著名数学家华罗庚曾针对数形结合思想作了一首著名的诗：“数缺形时少直观，形少数时难入微.数形结合百般好，隔离分家万事休.”数形结合，主要指的是数与形之间的一种对应关系.数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，达到“以形助数”或“以数解形”， 即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题形象化.我们在解决函数、三角函数、平面向量等问题的过程中，经常会遇到这样的一种困境：做题时总是感觉式子比较抽象，不容易理解，想来想去都没有头绪.此时便需要我们将其具体化，而具体化最好的途径便是借助图像.利用数形结合的思想可使所要研究的问题化难为易、化繁为简.把代数和几何相结合，能促进代数问题与图形之间的相互表征，使我们能较快地从所给问题的情境中探究出熟悉的模型，从而迅速、准确、科学地解决问题．

应用1：数形结合在比较大小问题中的应用

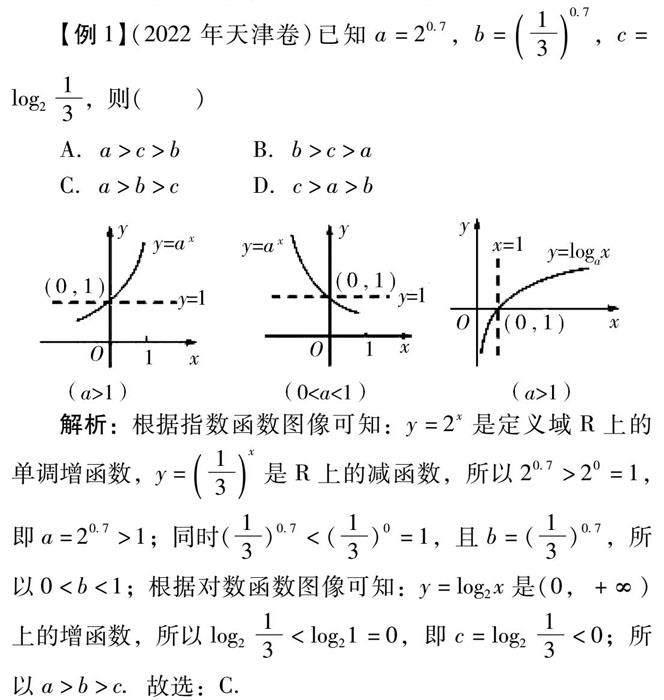
【例1】（2022年天津卷）已知a=207，b=1307，c=log213，则（  ）

A.a>c>b   B.b>c>a

C.a>b>c  D.c>a>b

解析：根据指数函数图像可知：y=2x是定义域R上的单调增函数，y=13x是R上的减函数，所以207>20=1，即a=207>1；同时（13）07<（13）0=1，且b=（13）07，所以0b>c.故选：C．

点评：在做题的过程中，我们经常会遇到比较大小问题，这类题中出现的每个数往往是不能计算出具体值的，我们只能借助函数图像的性质来辅助我们进行求解，如果题目比较简单，我们只需利用熟知的基本初等函数的图像即可求解，如果题目复杂，我们还需通过求导研究函数的单调性，再结合函数的草图去进一步求解．

【变式1】已知正实数a，b满足12a=log2a，13b=log2b，则（  ）

A.a

C.b<1

解析：依题意，在同一坐标系内，分别作出函数

y=（12）x，y=13x，y=log2x的图像（如上图），结合图像可得：1

应用2：数形结合的思想在函数最值或不等式问题中的应用

【例2】（2023年上海虹口高三阶段测试）已知函数f（x）=x-lnx，x>0

x+4e，x≤0若存在x1≤0，x2>0使得f（x1）=f（x2），则x1f（x2）的最小值为     ．

解析：当x>0时，f（x）=x-lnx，f′（x）=1-1x=x-1x，

当x>1时，f′（x）>0，当0

即当x=1时，f（x）取得极小值为f（1）=1.当x≤0时，f（x）=x+4e为增函数，且f（x）≤4e，由函数f（x）的图像得：设f（x1）=f（x2）=t，由题可知1≤t≤4e，由f（x1）=t得x1+4e=t，则x1=t-4e，则x1f（x2）=t（t-4e）=（t-2e）2-4e2，∵1≤t≤4e，所以当t=2e时，［x1f（x2）］min=-4e2.故答案为：-4e2．

应用3：数形结合在函数的切线问题中的应用

【例3】（2021年新高考Ⅰ卷）若过点（a，b）可以作曲线y=ex的两条切线，则（  ）

A.eb

B.ea

C.0

D.0

解析：数y=ex是增函数，函数的图像如图所示，切点在x轴上方．

如果点（a，b）在x轴上或x轴下方时，有且只有一条切线；如果点（a，b）在曲线y=ex上，有且只有一条切线；如果点（a，b）在曲线左上方，则没有切线；由图像可知，点（a，b）在图像的下方，且在x轴上方时，有两条切线，所以0

点评：通过本题不难发现，对于过某点作已知曲线的切线问题，可以借助函数图像判断切线的大致位置，通过分类讨论一一排除不符合要求的情况，最终得到需要的答案.这种方法对于解决解析几何类似的问题同样适用．

应用4：数形结合在函数零点问题中的应用

【例4】（2023年河南新乡市三模）已知函数f（x）=xex，若函数f（x）=［f（x）］2-m［f（x）］+m-1有3个不同的零点，则实数m的取值范围为（  ）

A.（0，1）      B. -1e，0

C.1-1e，1   D.1-1e，1∪（1，+∞）

解析：因为f（x）=xex，所以f′（x）=ex+xex=（x+1）ex，令f′（x）>0，得x>-1，令f′（x）<0，得x<-1，

所以f（x）在（-∞，-1）上是减函数，在（-1，+∞）上是增函数，所以f（x）min=f（-1）=-1e.

又因为当x<0时，f（x）=xex<0，当x>0时，f（x）=xex>0，f（x）的图像如图所示：

则f（x）有3个不同的零点，即关于x的方程［f（x）］2-m［f（x）］+m-1=0

有3个不同的实数根.令t=f（x），则t2-mt+m-1=0，解得t1=1，t2=m-1.由图可知方程f（x）=1有一个正根，因为方程F（x）=0有3个不同的实数根，所以方程f（x）=m-1有两个不相等的负根，

所以-1e

应用5：数形结合在含绝对值的三角函数中的应用

【例5】（2023年山东高三统考）已知函数f（x）=sin x+cos x+｜sin x-cos x｜，下列结论正确的是（  ）

A.函数图像关于x=π4对称

B.函数在-π4，π4上单调递增

C.若｜f（x1）｜+｜f（x2）｜=4，则x1+x2=π2+2kπ（k∈Z）

D.函数f（x）的最小值为-2

解析：由题意可得：f（x）=sin x+cos x+sin x-cos x

=2cos x，sin x

2sin x，sin x≥cos x

=2cos x，x∈-34π+2kπ，14π+2kπ

2sin x，x∈14π+2kπ，54π+2kπ

（k∈Z） ，

即可绘出函数图像，如下所示：

故对称轴为x=π4+kπ（k∈Z），A正确；

由图像易知，函数在-π4，0上单调递增，0，π4上单调递减，B错误；

要使｜f（x1）｜+｜f（x2）｜=4，则f（x1）=f（x2）=2，由图像可得x1=2k1π或x1=π2+2k1π、x2=2k2π或x2=π2+2k2π（k1，k2∈Z），故x1+x2=2kπ或x1+x2=π2+2kπ或x1+x2=π+2kπ（k∈Z），C错误；

当x=5π4+2kπ（k∈Z）时，函数取最小值，最小值f（x）min=-2，D错误.故选：A．

点评：通过本题我们不难发现，对于给定类似于函数y=｜sin x±cos x｜、y=｜sin x+cos x｜+｜sin x-cos x｜等函数解析式，可以先去掉绝对值，再画出图像，从而利用数形结合思想来求解相关问题，可通过学习这一道题会一类题的效果.未来我们也可以用同样的方法来研究稍复杂型带绝对值的同类题型求解．

应用6：数形结合思想在三角函数求ω问题中的应用

【例6】（2022年山西运城高三联考）已知函数f（x）=cos ωx-3sin ωx（ω>0），若f（x）在区间［0，2π］上有且仅有4个零点和1个极大值点，则ω的取值范围是（  ）

A.53，2312

B.1912，136

C.53，136 D.1912，116

解析：f（x）=cosωx-3sinωx=2cos（ωx+π3），令t=ωx+π3，由x∈［0，2π］，则t∈π3，2πω+π3；

因为f（x）在区间［0，2π］上有且仅有4个零点和1个极大值点，即y=2cos t在π3，2πω+π3上有且仅有4个零点和1个极大值点.作出y=2cos t的图像（如图所示），

则7π2≤2πω+π3<4π，解得1912≤ω<116，

故ω的取值范围是1912，116.故选：D．

点评：通过本题我们不难发现，在三角函数已知零点或极值点求ω，往往可以利用数形结合的思想来作图求解，对于较复杂的函数，则可通过诱导公式或三角恒等变换公式，将其转化为形如y=Asin（ωx+φ）+b等形式，再将ωx+φ看成一个整体，进而结合正、余弦函数的图像与性质求解，我们要通过学习这一道题，掌握好解题通法，达到会解一类题的效果．

应用7：数形结合在三角函数求图像交点相关的问题中的应用

【例7】（2023年福建龙岩高三统考）函数f（x）=1+cos12-xπ+xsin（1+x）π在区间-72，112上的所有零点之和为（  ）

A.6   B.8   C.12   D.16

解析：由题意可得：f（x）=1+cos12-xπ+xsin（1+x）π=1+cosπ2-πx+xsin（π+πx）=1+sin πx-xsin πx，

令f（x）=0，且f（1）=1≠0，可得sin πx=1x-1（x≠1），∵y=sin πx与y=1x-1均关于点（1，0）对称，

由图可设y=sin πx与y=1x-1的交点横坐标依次为

x1，x2，x3，x4，x5，x6，x7，x8，根据对称性可得

x1+x8=x2+x7=x3+x6=x4+x5=2，故函数f（x）

在-72，112上所有零点之和为2×4=8.故选：B．

点评：数形结合处理函数零点相关的问题，若给定的函数不能直接

求解或不能直接画图，则需通过分解转化，将一个函数的零点问题，转化为为两个函数图像交点的问题，然后数形结合，看其交点的个数有几个，其中交点的横坐标有几个不同的值，或判断横坐标之间有何关系，然后再进一步解决问题．

应用8：数形结合在平面向量隐圆问题中的应用

【例8】（2023年吉林市三模）已知，是单位向量，且·=0.若向量满足--2=1，则的最大值是   ．

解析：由·=0，得⊥，建立如图所示的平面直角坐标系，

则OA==（1，0），OB==（0，1），设=OC=（x，y） ，由--2=1，

得（x-1）2+（y-2）2=1 ，所以点C在以Q（1，2）为圆心，1为半径的圆上．

所以||max=｜OQ｜+1=5+1，故答案为：5+1．

数形结合是重要的数学思想，又是常用的数学方法.把数量关系的研究转化为图形性质的研究，或者把图形性质的研究转化为数量关系的研究，这种解决问题过程中“数”与“形”相互转化的研究策略，往往能够使困难问题简洁化、抽象问题详细化，能够变抽象思维为形象思维，有助于挖掘数学问题的本质，它是数学的规律性和敏捷性的有机结合．

【本文系全国教育规划课题（教育部重点课题）“粤港澳大湾区背景下中学拔尖创新人才高中-高校贯通式培养的路径研究”（立项号：DHA230397，主持人：叶丽琳）研究成果】

责任编辑  徐国坚