情境启发探究，合作促进创新

刘培杰

[ 摘 要 ]如何借助情境激发学生的探究兴趣，让学生在合作学习中形成良好的创新意识呢？文章以“锐角三角函数”的教学为例，从“创设情境，激趣启思”“理性归纳，建构新知”“问题设置，促进迁移”“适当启发，拓展延伸”等方面展开教学，并谈几点思考：生活化的情境可激发探究欲，关联问题可发展数学思维，互动交流是促进创新的动力，“问题化”总结新颖且有意义.

[ 关键词 ]情境；探究；合作；创新

数学对发展学生的思维与创新能力具有重要作用.创设恰到好处的情境能触动学生的内心，激发学生对知识的探索欲；和谐、民主的合作学习可发散学生的思维，促进创新意识的形成[1].为了验证这种说法，笔者在这方面做了大量研究，现以“锐角三角函数”的教学为例，与同行交流.

教学简录

1.创设情境，激趣启思

结合学生认知发展规律，初中数学课堂常用的情境有问题情境与思维情境等，这些情境都是激发学生学习兴趣，使其产生探究行为，发展高阶思维的重要举措.同时，良好的情境会营造自由、民主的课堂环境，让学生有更广阔的表现空间.

情境创设 众所周知，测算的应用十分广泛，如测算隧道的方向、平行岸的宽度、飞机与地面的距离、月球和地球的距离……

如图1，今天我们就一起来探讨如何测算旗杆的高度.已知测架AD的高度为1米，你能根据图中所标示的数据推算出旗杆EB的高吗？

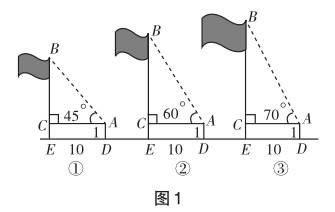
要求学生以小组合作学习的方式探讨这个问题，每组派一名代表将组内研究成果展示出来.

组1：前两幅图可以推导出旗杆的高度，但第三幅图不行.具体过程为：

组2：我们组赞同前两幅图的测算方法，但认为第三幅图中的旗杆高度也能推导出来，且与前两幅图所用方法类似.既然∠CAB的度数是确定的，那么AC∶BC的值必然也是恒定的，旗杆高度就可以计算出来，但我们不知道计算方法是怎样的.

组3：同意组2的观点，问题是我们不会计算.

师：你们是如何确定当∠CAB的度数确定时，AC∶BC的值是恒定的呢？

生1：（操作几何画板）如图2，已知Rt△ABC中的∠A为70°，无论点B与点C的位置在哪儿，AC∶BC的值恒定不变.

生2：即使知道它们的比值不变，也求不出旗杆的高度呀.

生3：若获得AC∶BC的近似值，或许就能获得BC的值.

师：很好！那有没有办法获得AC∶BC的近似值呢？

生4：只要能测量出AC，BC的长度即可.根据图2所显示的原理，只要能准确地画出任意一个三角形，并测出AC，BC的长度，那所获得的比值与原图是相等的.

在这种理念的驱使下，学生自主画图、取值、计算，发现当∠CAB为70°时，AC∶BC的值可能是无理数，难以获得精确值，那么计算而来的旗杆高度也只能取近似值.

2.理性归纳，建构新知

教师充分肯定了学生在上一个环节的表现，并与学生再次确认当∠CAB=70°时，获取旗杆高度的方法.接下来教师趁热打铁，要求学生分析“当∠CAB=41°时，BC∶AC的值也是确定的吗”.学生一致表示确定.在此基础上，教师设计了一张表格投影到电子白板上，让学生填写BC∶AC的值（见表1），并说说比值与∠A的关系.

生5：如图3，通过画图并对应表格数据来看，BC∶AC的值会随着∠A度数的变化而改变，若∠A确定了，那么BC∶AC的值就是恒定的，这与之前接触过的函数关系一致，即BC∶AC可理解为∠A的函数.

3.问题设置，促进迁移

问题是数学的心脏，数学学习离不开问题的引导.教师精心设计问题串，可让学生从更深层次内化新知，形成技能，促进知识的迁移与创新意识的发展.

问题1 （1）在Rt△ABC中，∠C为直角，AC=15，BC=8，分别求∠A，∠B的三角函数值.

（2）在△CDE中，已知DE=6，CE=8，CD=10，试求∠D的三角函数值.

（3）已知△ABC中，AB=AC= 5，BC=6，求sin∠B，tan∠A.

分析 问题（1）需先确定斜边的值；问题（2）需判断△CDE是否为直角三角形；问题（3）需通过作高来构造直角三角形.这三个问题成功地开启了学生的思维，让学生通过问题的解决，进一步夯实了知识基础.

师：是否能以BC为轴作对称？（答案是否定的）想要获得sin2α，必须求出x，y的值，该怎么求呢？

生7：可借助三角形相似与勾股定理来列方程组求解.

学生交流，并总结：sinα，cosα，tanα均为独立的个体，符号不可随意分割，不可将它们视作sin？α，cos？α，tan？α. sin 2α≠2 sin α，同理，tan（α+β）≠tanα+ tanβ.

学生的思维非常活跃，对这部分知识的理解相当透彻.此时，教师要求学生思考本节课为什么要研究直角三角形的锐角三角函数，并分析其本质、求解注意事项等.

4.适当启发，拓展延伸

师：大家对本节课的教学还存在什么想法与问题吗？

此问意在让学生通过对本节课的回顾、总结、反思，提出自己的看法.在这个问题的启发下，学生提出如下疑惑：①为什么直角三角形的锐角存在三角函数，而钝角与直角却不存在三角函数呢？②41°，70°的三角函数值能准确求出来吗？③要测量一座山的高度，但无法进入山底，该怎么构造直角三角形呢？④地球与月球的距离那么远，是否可以通过构造直角三角形来解决距离问题呢？

学生所提出的每一个问题都具有现实研究意义，由此也可以看出学生处于思考的状态，这是促进创新的基础.当然，课堂时间是有限的，教师不可能在课堂上逐一探讨每一个问题.因此，笔者挑选出几个具有代表意义的问题要求学生课后查阅资料、合作交流，争取自主答疑解惑.

教学感悟

1.生活化的情境可激发探究欲

生活化的情境与学生的生活息息相关，以此作为教学的起点，往往能成功激发学生的探索欲.测量旗杆的情境源自学生的实际生活，学生虽然都见过旗杆，却从来没有想过要测量它的高度，这个情境成功地激起了学生的探索兴趣，让学生对本节课充满了渴望.

2.关联问题可发展数学思维

面对情境中呈现的三幅图，学生经过自主探索发现前两根旗杆的高度能顺利求出，但第三根旗杆却无法快速求出，由此引发了AC∶BC是否为确定值的问题，近似值也自然生成.该情境成功引起了学生的认知冲突，让学生产生了更多思考，创新意识也在思维的不断深化中萌发.通过合作交流与探索，学生不仅发现了蕴含其中的规律，还体验到了学习带来的愉悦，建立了学习信心.

3.互动交流是促进创新的动力

教师着重应用合作交流的方式进行授课，学生积极思考，表达自己的观点，各组将组内成果与大家共享，加速了解决问题的进程，也优化了学生的思维，让信息加工变得更为深入[2].学生的群体认知随着交流的深入变得更加深刻，这不仅刷新了学生原有的知识，还帮助学生建构了新的知识网络，这是传统“注入式”教学无法达到的教学成效.交流时，师生、生生积极地表达自己的观点，呈现出较多的思维亮点，作为教师，不仅捕捉到了学生的发光点，还给予积极的引导与启发，开启了学生的思维，激发了创新意识，高质量课堂也在互动中动态生成.

4.“问题化”总结新颖且有意义

课堂尾声，在教师的启发下，学生自主提出一些高质量且具有探究价值的问题，让课堂总结显得新颖且有意义.“问题化”的课堂总结不仅引发了学生的思考，也引起了笔者的反思：究竟该如何满足学生的好奇心？通过怎样的方式才能有效提升学生的思维品质？

总之，精心创设教学情境为学生的探究搭建了良好的平台，自主探索与合作交流是开阔学生视野、促进学生掌握新技能、提炼学习方法、积累学习经验的重要方式.情境启发探究、合作促进创新的课堂充满了灵气与智慧，是促进学生全面发展的重要途径.

参考文献：

[1]冯卫东.“自学·议论·引导”教学法的基本原理与操作要义[J].课程·教材·教法，2011，31（05）：43-48.

[2]唐怀萍，都日娜.探究小组合作下初中数学纠错能力实施策略[J].数学学习与研究，2019（17）：86.