基于“8”字模型的变式拓展

何勇

[ 摘 要 ]文章从教材上图形简单的习题切入，立足“8”字模型进行变式拓展、逐步探究、发散延伸、激发兴趣，挖掘知识点之间的联系，使学生熟练掌握全等三角形的判定.通过变式深挖教材习题的价值，跳出题海、寻找规律、减轻负担、触类旁通，能让学生对“8”字模型融会贯通、灵活运用，并掌握基本模型、强化模型意识、丰富知识结构、提升思维能力，提高分析问题、解决问题的能力.

[ 关键词 ]习题变式；全等三角形；“8”字模型；模型思想

基金项目：中山市教育科研2023年度青年项目课题“新课标下基于项目式学习的初中数学解决问题的教学研究”（C2023042）.

徐利治教授的《数学方法论选讲》一书谈到，数学模型是指采用形式化语言反映特定问题或特定具体事物系统的数学关系，是运用数学的语言和工具对现实世界一些信息进行适当的简化.模型思想是学生体会和理解数学与外部世界联系的基本途径，模型的建立能帮助学生从具体到抽象、从抽象到本质感悟数学思想.模型的感悟过程就是学生数学思维发展的动态过程.

几何模型是指带有明显特征的典型图形，它是我们快速找到突破口、作出辅助线、完成几何构图从而解决综合问题的关键.“8”字模型的结构特征明显，看似简单，但在复杂几何图形的推导中往往有巧妙的作用，是连接知识的载体，承载着丰富的知识内涵.它在全等与相似中应用广泛，是探究角相等、线段相等的一种工具，是初中阶段最重要、最常见的几何模型之一，有助于提高解题效率.

“8”字模型应用广泛、变式灵活，学生可在不同的情境中识别和构建“8”字模型，从中体会数形结合、转化、分类等数学思想方法；经历数学建模的过程，从变中发现不变，从不变的数学本质中探究变的规律，可见其是学生数学素养培养的良好载体.下面以一节全等三角形的复习课为例予以阐述.

内容分析

全等三角形是初中几何的重点，是证明边或角关系的重要工具.全等三角形的学习不仅关系到三角形的学习，更关乎四边形等众多几何的学习，所以其在整个初中阶段具有承上启下的作用.运用“8”字模型证明三角形全等的知识、方法和技巧更是研究几何图形的重要基础，其应用十分广泛，在相似综合性问题中识别、构造“8”字模型更是历届教与学中的疑难问题，一直是中考数学必考内容之一.因此，在中考复习阶段总结并提炼“8”字模型十分重要.

学习目标

1.触类旁通，掌握全等三角形的判定方法，熟练运用“8”字模型解决综合问题，增强应用意识.

2.变式拓展，初步形成几何直观，强化模型意识，提升推理能力，获得思考乐趣，发展数学核心素养.

重点和难点

1.学习重点：获得分析和解决问题的基本方法，快速识别出“8”字模型，体验方法的多样性.

2.学习难点：掌握构建“8”字模型的作辅助线技巧，锻炼利用“8”字模型解决综合问题的意志，提高实践能力.

教学实施

1.简单习题做铺垫——初步识别“8”字模型

教师出示题目和图形，铺垫课堂.题目：如图1，AC和BD相交于点O，OA=OC，OB=OD，求证：AB∥DC（人教版教材八年级上册第44页练习10）.

教学说明 从教材简单习题入手，图形是常见“8”字模型的原型，学生熟悉判定全等三角形的数学语言表述，能为后面变式、挖掘习题价值做铺垫.中考复习课应该通过一些虽简单但意义深远的题目，来帮助学生深挖问题本质，探究知识联系，构建数学模型，使学生通过学习，打开“8”字模型的大门，进入“8”字模型的知识领域，激发兴趣，启发思维，积极投入，实现知识的融会贯通.

2.问题开放增自信——进阶认知“8”字模型

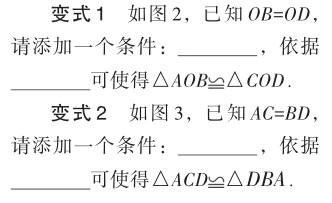
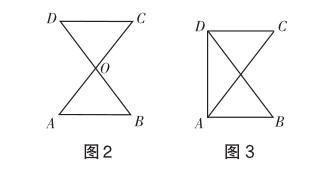
教学说明 教材例题、习题是学生发展的立足点，可借助习题中的简单图形，改变提问方式，让学生先思考后回答，总结归纳“8”字模型成立的条件.添加的条件不一样，依据的判定方法也不一样，这样能让学生全面复习全等三角形的判定方法.不同学生熟悉的全等三角形判定方法不一样，营造轻松、愉快的学习环境，能唤醒学生的知识记忆，激发学生的学习兴趣，增强学生的数学自信.学生进阶认知“8”字模型、巩固内化模型意识、增强主动参与学习的动力后，会乐意参与并积极投入到整节课的学习中.

3.变式练习拓思维——巧妙构造“8”字模型

教师同时出示变式3和变式4两道题及相应图形，并提问：题目条件有什么共同点？可以如何找“8”字模型？

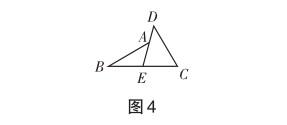
变式3 如图4，E是BC的中点，点A在DE上，且AB=CD，求证：∠BAE=∠D.

变式4 如图5，在△ABC中，AB=AC.点E在AB上，点F在AC的延长线上，且BE=CF，EF与BC交于点N，求证：EN=FN.

变式3和变式4看似与我们熟悉的“8”字模型没有关系，但条件或问题中出现中点时，实则隐藏着我们熟悉的“8”字模型.这是本节课的延伸.倍长中线是常见的辅助线，全等三角形对应边相等的代换是解决本题的关键.图形在改变，但不变的依然是全等三角形的判定和性质，本质就是“8”字模型.“8”字全等三角形模型是证明线段相等的一种方法，有时没有全等三角形，此时可以借助辅助线，通过构造我们熟悉的几何模型来解决问题.证明全等三角形的方法很多，不同层次的学生熟悉的判定方法不同，思考方式也不同，所作辅助线也不同.

实际上两道习题都还可以通过问题和条件互换等方式进行变式拓展，启发学生思考探究，使学生乐意投入到探索性的数学活动中，让不同的学生得到不同的发展.上述过程能让学生认识到“8”字模型的应用价值，初步学会在具体情境中思考运用学过的数学知识来分析、解决问题，提高实践能力，增强“8”字模型的应用意识.

接下来，教师出示变式5的题目和图形，小组讨论后看哪个小组说的思路和方法多.

变式5 如图6，在四边形ABCD中，∠B=∠C=90°，AN平分∠BAD，DN平分∠ADC，试探索AB，AD，CD之间的数量关系.

学生通过交流讨论、猜想验证、推理证明，感受“8”字模型在探究线段相等中的巧妙运用.一题多解不仅能使学生更牢固地掌握和运用所学知识，把学过的知识和方法使用自如、融会贯通；更能在分析、比较、寻找解题最佳途径的过程中培养创造性思维能力.多一些一题多解的变式练习，能让学生在变中求进、举一反三，能帮助学生总结、提炼通性通法，能培养学生的发散性思维.循序渐进，对巩固知识、增强解题能力、提高学习成绩、培育数学素养大有益处.学生经历从不同角度分析、解决问题，在研究图形性质、借助图形思考问题的过程中，会发现不变的本质就是“8”字模型，进而融会贯通，初步建立“8”字模型的几何直观，强化逻辑推理，通过会一道题懂一类题，内化模型意识，发展数学核心素养.

4.综合探究促发展——融会贯通“8”字模型

题目 在矩形ABCD中，AB= 2BC.E是直线AB上一点，F是直线BC上一点，且满足AE=2CF，连接EF交AC于点G.

（1）tan∠CAB= .

（2）如图10，当点E在线段AB上，点F在BC的延长线上时，

①求证：EG=FG；

②试探究CG与BE的关系.

（3）如图11，当点E在BA的延长线上，点F在线段BC上时，记AC与DF相交于点H.

①试说明EG=FG的结论仍然成立；

②当CF=1，BF=2时，求出GH的长.

教学说明 无论“8”字模型身处何地，学生都能精准地识别出来，哪怕它的形态发生改变，学生也能抓住“8”字模型的本质特征，通过添加辅助线灵活地重新构造，让问题通过转化得到解决.

解题的时候选择合适的模型，能够让解题事半功倍.全等三角形的“8”字模型在中考数学中往往是证明几何综合题的桥梁，时常和特殊四边形的基本性质、三角函数、勾股定理、相似三角形、圆、函数等综合考查.解决此题时，需要运用知识之间的密切联系，学生经历从条件和问题出发，猜想验证、大胆尝试，感受“8”字模型在全等三角形、相似三角形的拓展融合中的应用，自主强化基本模型的灵活运用、综合提升.教师要引导学生认清问题的核心，掌握作辅助线构建“8”字模型的思想方法，培养学生思维的灵活性与延展性，提高解题效率，助力学生构建完整的知识体系.

教学反思

1.反思积累，树立模型意识

罗增儒教授曾说，“要善于对新问题展开联想，辨别其是否属于某个类型，如果不直接属于则进行变化，使之属于某个类型”.巧作辅助线构造基本模型，或进行图形分解识别隐含的基本模型，是解决几何综合问题的关键与桥梁.解几何题时，教师要引导学生积累所学的基本图形，把图形的基本特征和构造方法进行加工提炼，得出通用的几何模型.解题时选择合适的模型，能够让解题事半功倍，进而提升解题能力.

强化几何模型的总结和训练，是培养学生的几何直观、逻辑思维和推理能力的重要方法和途径.虽说得模型者得几何，但是需要在几何解题中不断积累、总结，通过展开表征联想、巧作辅助线构造、图形简化重组等展现基本模型，使学生牢固掌握相关的数学模型，切实加强数学模型意识的培养.

2.整合优化，强化思想方法

几何综合题是对学生综合知识的应用考查，对学生的逻辑思维和分析推理能力有着较高的要求.在学习过程中，学生要循序渐进，明确条件特点、图形特征，巧作辅助线将几何图形转化为自己熟悉的基本模型，渗透模型思想和转化思想，灵活使用思想方法寻找解决问题的基本策略.解题的目的不在于解题本身，而在于学习其中的解题方法，然后将其上升到思想高度，获得思想的提升.教师要引导学生在数学思想的引导下探寻解题策略，反思解题过程，提炼解题思想.

将模型思想融入初中数学教学中，有助于深化学生对数学知识本质的理解，有助于学生掌握运用数学知识解决问题的思路与方法，能促进学生学习能力的进一步提升.复习几何综合题时，教师应结合学生的认知规律进行例题精练、系列变式，设计思考环节，深挖隐形模型，合理铺垫搭建梯子，减缓解决问题的思维坡度，让数学思想与思维方法在课堂上更好地生根发芽.学习并运用模型思想，是学生提高思维能力、发展数学素养必不可少的训练.

3.拓展应用，发展数学素养

“8”字模型在从全等三角形到相似三角形的拓展融合中的应用，通过变式优化知识结构，螺旋上升地理解和掌握一系列数学知识；以点带面分析和解决一连串数学问题；多题归一提炼和生成一系列通性解法.鼓励学生模仿表达、创新变式，提升感官认识，严谨推理逻辑，激发学习兴趣，延伸课程应用，内化渗透重要的思想方法，领悟万变不离其宗的数学本质，让学生减轻学习负担，增强数学学习兴趣，获得成功自信.

学习最好的方法是经历思索探究后的自我领悟、自主构建、自然发展.在复习教学中，教师要确定教学主线贯穿课堂、整理知识、归纳题型，引导学生重回知识起点，在已有的认知水平上，挖掘知识间的本质联系，分析题目中的隐含条件，掌握问题的内在特征.学生在变式拓展的学习中不断深化探究，加强思维的渗透和方法的提炼，真正做到活学活用、融会贯通、循序渐进、拓展提升；在一题多解的思考中激活认知结构，激发求知欲望，主动体验知识的发生和发展过程，丰富知识体系，使不同的人在数学上得到不同的发展；在多样、全面的探索中强化几何直观，提炼熟悉模型，掌握思想方法，学会思考，严谨推理逻辑，提升思维能力，发展数学核心素养.