路基不均匀沉降与刚度变异联合作用影响分析

裴彤彤 张加宝 李宏洲 马帅 卫佳

摘 要：为探究无砟轨道路基不均匀沉降与刚度变异对行车安全性和轨道服役性能的影响规律，文章以CRTS Ⅲ型板式无砟轨道为研究对象，基于有限元方法建立CRTS Ⅲ型板式无砟轨道非线性分析模型，研究路基不均匀沉降作用下轨道结构的变形规律；结合多体动力学方法，建立车辆-轨道-路基耦合系统动力学模型，分析沉降作用及刚度变异作用下车-线-路基耦合系统动力响应。结果表明：随着沉降幅值的增大，会逐渐出现脱空；随着沉降波长的增大，将会减小无砟轨道与路基表层间的沉降差异；在路基不均匀沉降和扣件刚度变异联合作用下，扣件刚度增加，钢轨的垂向位移减小，轨道板上拱变形增大；联合作用会增大动力响应，对车辆运行安全和轨道结构受力造成影响。

关键词：路基不均匀沉降；刚度变异；有限元分析；车辆动力学性能

中图分类号：U271 文献标志码：A

0 引言

无砟轨道在高速铁路建设中应用广泛，具有高平顺性、稳定性和低维修量的优点。CRTS Ⅰ型、CRTS Ⅱ型和CRTS Ⅲ型板式无砟轨道在铁路建设中应用广泛。CRTS Ⅲ型板式无砟轨道是铁路建设中常用的轨道类型之一，能减缓基础变形、降低维护工作，保持高稳定性和平顺性。但由于其整体刚性强，对基础结构变形敏感，仅能通过扣件调整几何形状。受土壤差异、填料不均、地下水影响，路基不均匀沉降难以避免。大幅度路基沉降会导致脱空现象，严重时影响行车安全。下部刚度变异会放大冲击作用，加剧轮轨间冲击力，损害行车安全。

目前，研究多关注无砟轨道在高速铁路建设中的关键问题。李国芳等[1]研究了扁疤-路桥过渡段不均匀沉降与刚度变异联合作用下车辆动力特性分析。郭宇等[2-3]研究了无砟轨道轨面变形与路基沉降的映射关系，轨下局部脱空状态的影响，以及板式无砟轨道对路基不均匀沉降的敏感性。张乾等[4]探究了无砟轨道路基不均匀沉降区、高速列车动力特性的变化情况，并强调了车体的垂向加速度对路基沉降幅值的敏感性。Chen等[5]进行了不同类型的无砟轨道的动态性能比较研究，发现动力学响应随着车速增加而增加，垂直紧固件刚度增加则减少钢轨位移。Guo等[6]研究了中国高速铁路的车辆-轨道-路基系统在路基沉降差异情况下的动态评估和混凝土轨道结构的滤波效应，以及车辆荷载引起的特殊动态响应。

文章综合考虑了无砟轨道在高速铁路建设中的多个关键问题，特别是针对CRTS Ⅲ型板式无砟轨道，结合路基不均匀沉降和刚度变异的联合作用进行了深入研究。通过建立有限元模型，运用动力学仿真软件，系统性分析了轮轨病害对车辆动力学性能的影响。此外，文章还突出了对路基不均匀沉降波长、幅值与钢轨、轨道板、底座板之间的关系，以及在模拟刚度参数变化的基础上分析刚度变异对车辆动态性能的影响。总结路基不均匀沉降和刚度变异联合作用对车辆系统动力学性能的影响，并提出解决方案，为相关领域的进一步研究提供帮助。

1 路基不均匀沉降下列车-轨道-路基间相互作用基本原理

1.1 路基不均匀沉降作用原理

当路基发生不均匀沉降时，会导致无砟轨道表面发生垂向差异变形，使轨面变得不平顺。由于无砟轨道具有较高的刚度和整体性，其相对于路基来说具有更强的抵抗基础变形能力[7]。然而，这也会导致无砟轨道和路基之间的变形不协调，可能引发局部脱空甚至空吊现象。

当局部脱空发生时，路基对无砟轨道的支撑效果会失效，导致力量转移到两侧区域，增加接触力并引起支撑刚度不均匀。高速列车通过不均匀沉降区域时，支撑刚度不平顺和轨面几何变形加剧了轮轨之间的相互作用，影响轨道结构和动力学性能，加剧路基沉降。列车通过脱空区域时，路基和无砟轨道之间会出现动态周期性循环，使得对这段区域的路基和无砟轨道间不断形成脱空-接触-脱空的动态周期性循环，这种“拍打”作用在列车长期的运营过程中，严重影响列车运行稳定性与安全性，同时对无砟轨道的使用寿命也有影响。

1.2 路基不均匀沉降模型模拟

路基不均匀沉降可分为余弦型、错台型和折角型3种形式[8]，其中余弦型是最主要的类型。错台型和折角型则常见于路基、隧道和桥梁过渡段。文章选择余弦型路基不均匀沉降进行模拟，在有限元模型中通过设定强制位移边界条件来模拟这种类型的沉降[9]，用下凹全波余弦型曲线来模拟路基的不均匀沉降，如图1所示。

余弦型曲线表达式为：

式中：Z 0 为铁路纵向在某位置处的路基沉降值，A为余弦型沉降幅值，S为余弦型沉降波长，X为发生路基不均匀沉降位置，X 0 为路基沉降起点。

2 CRTSⅢ型板式无砟轨道有限元模型

CRTSⅢ型板式无砟轨道是一种纵连板式结构，由钢轨、弹性扣件、轨道板、自密实混凝土、底座板和路基组成。钢轨与轨道板通过扣件系统连接，轨道板之间通过钢筋相互连接，自密实混凝土与轨道板之间存在层间黏结。底座板与自密实混凝土之间具有凸台和凹槽，通过咬合起到限位作用。底座板与路基面之间存在层间接触。参考铁路行业相关规范和文献资料[10-11]，CRTSⅢ型板式无砟轨道的各层结构参数，见表1、表2。

CRTSⅢ型板式无砟轨道有限元模型包括轨道模型和路基模型，其中轨道模型包括钢轨、扣件、轨道板、自密实混凝土、底座板；路基模型包括基床表层、基床底层、路堤本体。钢轨采用梁单元beam189模拟；扣件系统采用弹簧阻尼单元combin14模拟；轨道板、自密实混凝土、底座板、路基均采用实体单元solid185模拟。

设置层间约束条件，建模时假定轨道板和自密实混凝土层间接触良好，采用共节点处理，自密实混凝土和底座板的接触面采用凹凸槽咬合限位，并使用接触单元模拟二者间的黏接作用。在模型中，底座板和路基表层之间使用接触单元模拟黏接作用，以解决路基表层和无砟轨道之间的脱空、接触和轨道离缝等缺陷。另外，三层路基之间采用共节点进行黏接处理。

为了减小边界效应，路基不均匀沉降中心选在轨道中心处。模型长度设置为28.28 m，共5块轨道板，约束设置方面，轨道板两侧面和路基本体的底面都施加全约束。

3 基础结构变形特性及其影响研究

为了研究板式无砟轨道在路基不均匀沉降条件下的响应，对其进行有限元分析，考虑列车循环动态载荷和自身重力影响，研究各层结构的跟随性沉降、轨面的不平顺性，以及轨道结构的受力特性变化。特别需要关注各层结构间的几何形态、路基不均匀沉降的映射关系，以及沉降波长和幅值变化、扣件刚度的局部和整体突变对无砟轨道的影响。研究内容有助于评估轨道结构的力学性能。

3.1 板式无砟轨道映射关系

路基不均匀沉降发生时，由于轨道结构存在自重，钢轨，轨道板，自密实混凝土和底座板都会因为重力产生一定的跟随性变形。文章通过建立有限元模型和相关参数，分析了在静力平衡条件下，不同路基沉降幅值和沉降波长对CRTSⅢ型板式无砟轨道各层结构的几何变形规律。选择沉降波长为10 m，沉降幅值为 10 mm、20 mm 的余弦型沉降条件，对CRTSⅢ型板式无砟轨道在沉降强迫作用下的受力变形进行了研究。图2展示了路基不均匀沉降引起的板式无砟轨道各层结构的变形云图。在不均匀沉降区段内，随着沉降幅值的增加，轨道各层结构所受应力逐渐增大，最大应力对应沉降中心；路基表层承受的应力最大。

当发生路基不均匀沉降时，由图可知无砟轨道各层结构随着路基表层不均匀沉降的发生也随之产生跟随性变形，且在路基不均匀沉降达到最大值时，无砟轨道各层结构变形也随之达到最大。从图2分析，当路基不均匀沉降发生时，轨道板、自密实混凝土、底座板垂向变形基本一致，轨道结构没有发生跟随性变形，底座板和路基表层之间出现了脱空。对列车轨道系统安全稳定运行造成威胁。

3.2 沉降参数的影响

3.2.1 沉降幅值的影响

在路基发生不均匀沉降后，板式无砟轨道各层结构会发生几何变形，底座板与路基表层之间的脱空对无砟轨道的支撑刚度产生影响，从而劣化车辆运行的安全稳定性。因此，将以CRTSⅢ型板式无砟轨道为例，分析余弦型沉降的波长和幅值变化对沉降参数的影响。

在不均匀沉降中，选取沉降波长在10～25 m范围，研究沉降幅值从5 mm到25 mm，间隔为5 mm等间隔增大的情况下，板式无砟轨道的结构变形和沉降参数的变化规律。

图3为沉降波长一定的情况下，不同沉降幅值轨面变形图。可以看出随着不同幅值的余弦型路基不均匀沉降的发生，轨面的几何变形形式类似于余弦型变形，在沉降区域边缘两侧存在局部的上拱变形，这是因为随着沉降的发生，轨道结构由于其单元式的构造，会发生“杠杆作用”，从而形成图中沉降始末的上拱现象；并且随着沉降幅值的增大上拱变形的幅值也随之增大，在波长较短时这种现象尤为明显。

对于轨面沉降变形的影响，由图3可知，随着路基沉降幅值增大，钢轨的几何变形程度也增大。而且随着沉降波长的增大，轨道结构的杠杆效应减弱，所以轨道沉降两端的上拱变形也随之减小。当沉降波长较小时，轨面的垂向变形幅值小于沉降幅值，因此会发生明显的脱空，而当沉降波长比较大时，钢轨轨面的垂向变形幅值和沉降幅值基本相同，故随着沉降波长的增大，轨道结构层间会逐渐贴合，减小脱空的发生。当沉降幅值小于10 mm时，钢轨的垂向变形幅值与沉降幅值基本一致，表明轨道整体跟随良好。但当沉降幅值达到15 mm时，开始产生离缝现象。随着沉降幅值增大，无砟轨道的整体刚性使钢轨的变形逐渐小于路基，脱空量增大。

3.2.2 沉降波长的影响

在路基不均匀沉降中，选取间隔为5 mm，沉降幅值为5～25 mm，探究板式无砟轨道几何变形特性，研究随着路基不均匀沉降波长从10 m到25 m，间隔为5 m等间隔增大的过程中，沉降波长变化对轨道结构的影响。

图4为沉降幅值一定，沉降波长从10 m～25 m变化时轨面垂向变形曲线图，发现当波长为10 m时，尽管沉降幅值增大，但是其轨面垂向变形保持在5 mm左右；当路基沉降波长为20 m时，轨面垂向变形量大致等于路基沉降幅值，表明长波条件下钢轨-无砟轨道-路基面形成了一个可协调变形的多层结构，钢轨几乎与路基面发生同步沉降，沉降幅值完全映射至轨面。由此可以得出，当路基不均匀沉降幅值一定时，沉降波长的增大，将会减小无砟轨道与路基表层间的沉降差异，并减小脱空乃至空吊现象的产生，使无砟轨道的几何形态变形与路基不均匀沉降间保持较高的跟随性。当沉降波长小于20 m时，轨道处于悬空状态，沉降波长增大时轨道沉降量增大，轨面变形量随波长增大而增大；当沉降波长大于等于20 m时，无砟轨道急剧下沉，轨面出现更为显著的垂向不平顺，钢轨将产生与路基沉降幅值几乎相同的沉降量。

4 路基不均匀沉降与刚度变异对车辆系统动力学特性的影响研究

4.1 沉降幅值的影响研究

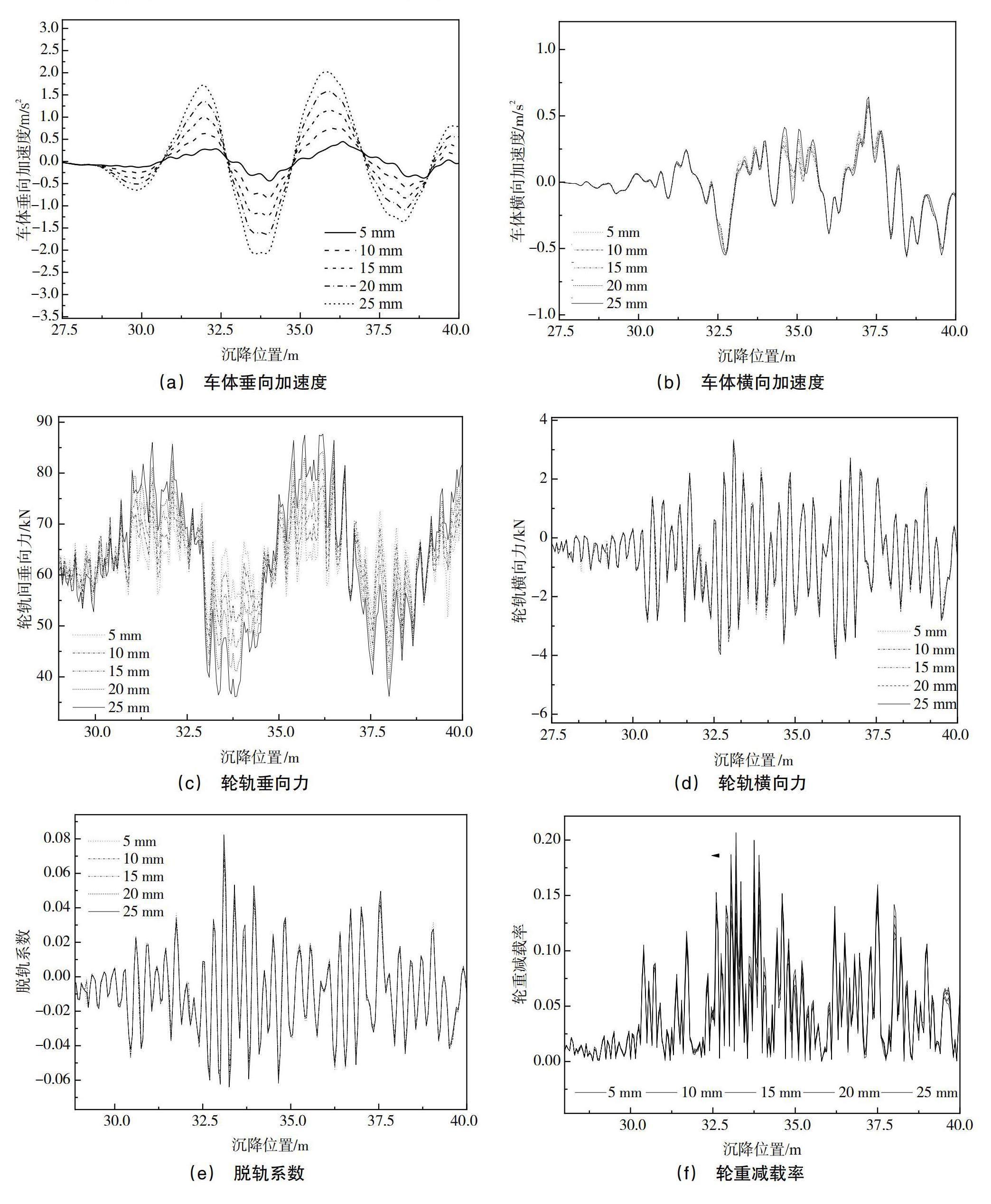
选取路基不均匀沉降波长为20 m，对沉降幅值由5 mm等间隔增加至25 mm时，这5种工况进行研究。计算在这5种工况下，车辆以200 km/h通过路基不均匀沉降区域时，路基不均匀沉降幅值的变化对车辆动力响应的影响，其中轨道随机不平顺谱选取高速铁路无砟轨道不平顺谱。图5和表3分别为路基不均匀沉降幅值对车辆动力学特性的影响；路基不均匀沉降作用下对车辆平稳性和稳定性的影响。

当路基不均匀沉降发生时，随着沉降幅值的增大，车体垂向加速度，车体横向加速度，轮轨垂向力，轮轨横向力，脱轨系数，轮重减载率都将有不同程度的增大。且相比较于横向的车体加速度，轮轨横向力来讲，车体垂向加速度，轮轨横向力增长幅值较大，这是由于当车辆通过路基不均匀沉降区段时，路基不均匀沉降为垂向方向的变形，主要影响的是车辆垂向的动力学特性。

当路基不均匀沉降波长为20 m时，沉降幅值由5 mm增大至25 mm时，对比在不同幅值下车辆的动力学特性，可以得出以下结论。

（1）当路基不均匀沉降波长为20 m时，沉降幅值从5 mm增大至25 mm的过程中，车体垂向加速度和横向加速度都增大。车体垂向加速度和横向加速度分别从0.455 m/s 2 和0.059 m/s 2 增大至2.034 m/s 2和0.064 m/s 2 。同样，轮轨垂向力和横向力也随沉降幅值增大，但垂向力的增幅明显大于横向力。这是因为余弦型路基不均匀沉降主要影响车辆的垂向动力学特性。

（2）从表3中分析车辆的平稳性，随着沉降幅值增大，横向Sperling指数和垂向Sperling指数也增大。沉降幅值从5 mm增大至20 mm时，横向Sperling指数和垂向Sperling指数分别从1.136和2.442增大至1.139和2.919。垂向Sperling指数的增幅更大，并且平稳性等级从优级劣化为合格级，对车辆动力学特性的影响更大。

（3）根据表中的数据，从车辆的稳定性方面分析，随着沉降幅值增大，脱轨系数和轮重减载率也增大。沉降幅值从5 mm增大至25 mm时，脱轨系数和轮重减载率分别从0.066和0.633增大至0.078 6和0.647；轮重减载率小于0.80，符合安全评定要求；脱轨系数小于0.8，也符合安全评定要求。

4.2 沉降波长的影响研究

同样，当路基不均匀沉降幅值20 mm，对沉降波长由10 m等间隔增大至25 m时，对这4种工况进行分析，探究4种工况对车辆动力学特性的影响。其他计算参数不变。

图6和表4为路基不均匀沉降波长对车辆动力学特性的影响；路基不均匀沉降作用下对车辆平稳性、稳定性的影响。

对图6和表4进行分析，当路基不均匀沉降幅值为20 mm时，沉降波长由10 m增大至25 m时，对比在不同波长下车辆的动力学特性，可以得出以下结论。

（1）当沉降幅值为20 mm时，轮轨垂向力对于沉降波长的变化更为敏感，相比于轮轨横向力。当沉降波长为10 m时，轮轨垂向力曲线变化较小，因为此时无砟轨道与底座板之间存在脱空，几何变形较小，对轮轨动力影响较小。当波长增大至15 m时，轮轨垂向力波形变化较大，峰值约为84 kN。当波长达到20 m时，轮轨垂向力波形较为平缓，因为此时上拱变形明显减弱，对轨道平顺性的影响较小。当波长达到25 m时，无砟轨道和路基的变形程度基本一致，轮轨间的相互作用逐渐减小，从整体趋势来看，波长较大时，轮轨垂向力较小。

（2）随着沉降波长的增大，横向Sperling指数、垂向Sperling指数和脱轨系数呈先增大后减小的趋势，最大值出现在20 m波长下，分别为1.138 8、2.919和0.078 6。然而，仍然满足安全评定标准。因此要对20 m波长不均匀沉降进行重点监控。

4.3 扣件刚度局部突变动力学性能研究

选定路基不均匀沉降，在沉降幅值20 mm，沉降波长为20 m的情况下，对无砟轨道扣件局部刚度突变数值，在1：1、1：2、1：5、1：10这4种工况下进行对比分析，探究扣件刚度局部突变对车辆动力学特性的影响。其他计算参数不变。图7和表5分别为路基不均匀沉降下，扣件局部刚度突变对车辆动力学特性的影响，以及对车辆平稳性、稳定性的影响。当路基不均匀沉降幅值20 mm，波长20 m时，扣件局部刚度比值由1：1增大至1：10，分析其对车辆动力学特性的影响规律如下。

（1）当路基不均匀沉降发生时，随着扣件局部刚度比值的增大，对于车体垂向加速度，车体横向加速度都随着扣件刚度比值的增大而增大，当扣件局部刚度比值由1：1增大至1：10时，车体垂向加速度和横向加速度均值由0.435 m/s 2 和0.108 m/s 2 ，增加至0.505 m/s 2 和0.127 m/s 2 。

（2）当路基不均匀沉降发生时，随着扣件局部刚度比值的增大，对于轮轨垂向力和横向力来讲，轮轨间的作用力是随之增大的，局部刚度比由1：1增加至1：5时，轮轨垂向力峰值变化由92.72 kN增大至92.77 kN。局部刚度比由1：5增加至1：10时，轮轨横向力峰值由3.25 kN增大至3.26 kN。两者的增加幅度有限，故扣件系统局部刚度突变对轮轨力影响较小。

（3）随着刚度局部突变比值的增加，横向Sper?ling指数没有明显的变化规律，但始终在安全评定范围之内，垂向Sperling指数随着扣件刚度比值的增大而增加，但增大幅度小于1%。其值始终在安全评定范围之内。表明局部刚度比值的增大对车辆平稳性影响不大。

（4）随扣件刚度局部突变比的增加，脱轨系数和轮重减载率虽然有所变化，但其波动幅值始终不超过3%，并且在最大值的情况下，不清楚值始终在安全评定范围之内。表明局部扣件刚度比值的增大对车辆稳定性影响不大。

4.4 扣件刚度整体突变动力学性能研究

选定路基不均匀沉降幅值20 mm，波长20 m的情况下，无砟轨道扣件刚度的突变倍频为1、2、5、10倍情况下，探究对车辆动力学特性的影响规律。其他计算条件不变。k=35 kN/mm。图8和表6为路基不均匀沉降下，扣件整体刚度突变对车辆动力学特性的影响。

对图8和表6进行分析，当路基不均匀沉降幅值20 mm，波长20 m时，扣件整体刚度由1 k增加至10 k，分析其对车辆动力学特性的影响规律如下。

（1）随着扣件整体刚度的增大，车体垂向加速度和车体横向加速度都随之增加，但是增加幅度有限，扣件整体刚度由1 k增加至10 k时，车体垂向加速度由0.435 m/s 2 ，增加至0.505 m/s 2 。车体横向加速度在扣件刚度由1 k增加至5 k时，由0.109 m/s 2 增加到0.144 m/s 2 。总体来说随着扣件整体刚度增大，车体横向加速度和车体垂向加速度随之增大，这将会对车体的振动特性造成影响。

（2）随着扣件整体刚度的增大，轮轨间的相互作用力也随之增大，当刚度由1 k增加至10 k时，从图8中可以看出轮轨垂向力是随之增加的，峰值变化由92.72 kN增加至92.80 kN。对于轮轨横向力来讲，当扣件刚度由原来的两倍增加至10倍时，其峰值由3.24 kN增大至3.31 kN，但是相比较于轮轨垂向力，其增加的幅度有限。最终结果表明随着扣件刚度的增大，轮轨之间垂向的相互作用加剧。

（3）随着扣件整体刚度的增大，垂向Sperling指数随着扣件刚度的增大而增大，但增大幅度有限。

横向Sperling指数虽存在一定变化，但变化程度很小。并且两者最大值均在安全评定范围之内，表明其对车辆平稳性影响较小。

（4）随着扣件整体刚度的增大，脱轨系数和轮重减载率都有所变化，但其值始终在一定范围内波动，其波动幅度小于3%，并且其最大值仍在安全评定范围之内。表明扣件整体刚度变化对车辆稳定性影响较小。

5 结论

近年来，关于路基不均匀沉降和刚度变异的研究已在国内外得到广泛关注。文章以CRTSⅢ型板式无砟轨道为研究对象，通过建立有限元模型和多体动力学模型进行有限元分析和动力学分析，得出以下结论。

（1）对于无砟轨道的几何变形来说，当沉降幅值较小时，轨道与路基之间的跟随性较好。但随着沉降幅值的增大，会出现脱空现象，且脱空范围会迅速扩大。沉降区域两侧的上拱变形幅值也随沉降幅值的增大而劣化，对列车安全和轨道性会造成威胁。

（2）当沉降波长较小时，轨面的垂向变形幅值小于沉降幅值，所以会发生明显的脱空，而当沉降波长比较大时，轨面的垂向变形幅值和沉降幅值基本相同，所以随着沉降波长的增大，将会减小无砟轨道与路基表层间的沉降差异，并减小脱空乃至空吊现象的产生，使无砟轨道的几何形态变形与路基不均匀沉降间保持较高的跟随性。当沉降波长达到20 m时，轨道结构会发生跟随性变形，脱空现象减小。

（3）在路基不均匀沉降和扣件刚度变异联合作用下，钢轨的垂向位移随扣件刚度增加而减小，而轨道板的上拱变形随扣件刚度增加而增大。

（4）动力学分析结果显示，当沉降幅值增大时，车体的振动加速度增大，特别是垂向加速度。轮轨间作用力加剧，轮轨垂向力和横向力也增大，同时Sperling指数、脱轨系数和轮重减载率也增大，对车辆平稳性和稳定性造成影响。沉降波长增大时，车辆的动力响应表现出轮轨垂向力先增大后减小的趋势。Sperling指数和脱轨系数也呈现先增大后减小的趋势，对波长的变化非常敏感，最大值在20 m处。

（5）在路基不均匀沉降和扣件刚度变异联合作用会增加车体垂向加速度、横向加速度、轮轨横向力和轮轨垂向力，对车辆运行安全和轨道结构受力造成影响。因此，在无砟轨道运营过程中，应及时维修扣件系统，保持刚度的合适范围和均匀性，以避免局部刚度突变对列车运行的影响。

参考文献：

[1]李国芳，王相平，丁旺才，等. 扁疤-路桥过渡段不均匀沉降与刚度变异联合作用下车辆动力特性分析[J]. 铁道学报，2022，44（4）：36-45.

[2]郭宇，高建敏，孙宇，等. 板式无砟轨道轨面变形与路基沉降的映射关系[J]. 西南交通大学学报，2017，52（6）：1139-1147+1215.

[3]郭宇. 高速铁路路基不均匀沉降及其演化对车辆轨道耦合系统力学性能的影响[D]. 成都：西南交通大学，2018.

[4]张乾，蔡小培，钟阳龙，等. 无砟轨道路基不均匀沉降区高速列车动力特性[J]. 西南交通大学学报，2023，58（1）：133-140.

[5]Chen M，Su Y，Zhun S Y，et al. Dynamic performance com?parison of different types of ballastless tracks using vehi?cle-track-subgrade coupled dynamics model[J]. Engineer?ing Structures，2021，249：1-16.

[6]Guo Y，Sun Q，Sun Y. Dynamic evaluation of vehicle-slab track system under differential subgrade settlement in chinas high-speed railway[J]. Soil Dynamics and Earth?quake Engineering，2023，164：1-13.

[7]崔旭浩. 路基不均匀沉降对CRTSⅡ型板式无砟轨道动力特性及损伤行为的影响[D]. 北京：北京交通大学，2022.

[8]朱兆铭. 路基不均匀沉降下双块式无砟轨道力学特性研究[D]. 南昌：华东交通大学，2023.

[9]闫斌，谢浩然，沈青川，等. 季冻区CRTSⅠ型无砟轨道不平顺规律及受力特性[J]. 哈尔滨工业大学学报，2021，53（3）：110-117.

[10]Jiang H G，Li Y X，Wang Y J. Dynamic performance eval?uation of ballastless track in high-speed railways under subgrade differential settlement[J]. Transportation Geo?technics，2022，33：100721.

[11]肖威，郭宇，高建敏，等. 高速铁路路基不均匀沉降对CRTS Ⅲ板式轨道受力变形的影响[J]. 铁道科学与工程学报，2015，12（4）：724-730.

Analysis of the Combined Effects of Uneven Subgrade Settlement and Variable Stiffness

PEI Tongtong 1 ，ZHANG Jiabao 2 ，LI Hongzhou 1 ，MA Shuai 1 ，WEI Jia 1

（1. Lanzhou Jiaotong University， Lanzhou Gansu 730070，China；2. Jiayuguan Depot of China Railway Lanzhou Bureau Group Co.， Ltd.， Jiayuguan Gansu 735100，China）

Abstract： ： To explore the impact of uneven settlement of ballastless track subgrade and stiffness variation on the safety of train operation and service performance of the track， the paper takes the CRTS III slab ballastless track as the research object， establishes a nonlinear analysis model of the CRTS III slab ballastless track based on the fi?nite element method to study the deformation characteristics of the track structure under the action of uneven sub?grade settlement. By combining the multi-body dynamics method， it establishes a dynamic model of the vehicle-track-subgrade coupled system to analyze the dynamic response of the coupled system under the effects of settle?ment and stiffness variation. The results show that with the increase of settlement amplitude， voiding will gradually occur; as the settlement wavelength increases， the settlement difference between the ballastless track and the sub?grade surface will decrease. Under the combined action of uneven subgrade settlement and stiffness variation of fas?teners， an increase in fastener stiffness will lead to a decrease in the vertical displacement of the rail and an in?crease in the arch deformation on the track slab. This combined action will increase the dynamic response， affecting the safe operation of vehicles and the stress on the track structure.

Key words： ： uneven subgrade settlement; stiffness variation; finite element analysis; vehicle dynamic perfor?mance